基于反激电路的无电解电容光伏逆变器*

苗国耀

(河南机电职业学院电气工程学院，河南 郑州 450000)

近年来，太阳能由于其显著的特征(如零污染，免费和易获取)已然成为化石燃料的替代品[1]。在光伏并网应用中，由于光伏板的某些物理特性和局限性，因此无法将PV 板产生的最大功率直接传输到电网。因此，需要在光伏板旁使用逆变器克服这些限制。光伏逆变器分为中央逆变器，串式逆变器和微型逆变器，其中微型逆变器更具吸引力，因为它们具有更高的性能，可从PV 板吸收最大功率，安装成本低，并且由于模块化而易于使用[2－3]。

然而，单相光伏逆变器的一个主要挑战是光伏侧存在二倍工频的脉动功率，降低最大功率点跟踪(Maximum Power Point Tracking，MPPT)性能和系统效率。为此，功率解耦方案应运而生，其大致分为无源和有源解耦两种。方案中，功率脉动部分均由电容处理。简言之，其功率解耦电路补偿光伏侧和交流侧之间的瞬时功率变化；当输出功率小于光伏功率时，功率解耦电路存储光伏的多余能量，反之亦然。图1 展示了采用功率解耦过程中能量的流动方向。为减少功率脉动，无源功率解耦的方案以其操作简单而被广泛采用，即PV 板两端直接并联电容器[4]。式(1)为满足要求所需解耦电容器的值[5]。

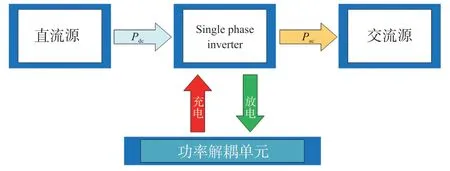
图1 功率流通路径

式中:Pdc是光伏组件的额定功率，f是电网频率，Vdc和ΔV分别是解耦电容器电压的平均值和波纹值。由于光伏电池板的电压较低，特别是在低功率电池板中，可接受的光伏电压纹波较小，根据式(1)，此方案所需电容较大，因此电解电容(E-caps)成为了首选。但此类方案势必降低微型逆变器的整体使用寿命[2]。在文献[6－11]中，通过增加解耦电容的平均电压或通过额外的元件增加电压纹波的方式以减小所需解耦电容值，达到薄膜电容替代电解电容的目的。但此类方案，即有功功率解耦策略，往往需额外的功率器件，增加了微型逆变器控制和结构的复杂性。

本文在反激电路的基础上，提出了一种新型串联功率解耦的光伏逆变器。该变换器是基于传统的反激变换器以补偿光伏侧的功率脉动，无需电解电容。所提拓扑结构有结构简单、额外元件少等优点。本文在详细介绍所提拓扑结构及其工作原理的基础上，分析了参数选择。最后，搭建了一个100 W 样机，对所提拓扑结构的可行性和理论分析的准确性进行了实验验证。

1 所提逆变器电路结构与工作原理

图2 为本文所提电路，其电路由反激电路演绎得到。详言之，直流电源由PV 板和滤波电容Cpv组成；功率解耦单元由反激电路(变压器T和二极管D3)和解耦电容C构成，以补偿输入与输出功率差值；S1－4和D1－2为本文逆变单元；Lf和Cf为LC 滤波器；最后通过MPPT 算法吸收光伏板的最大功率，并向电网输送电能。

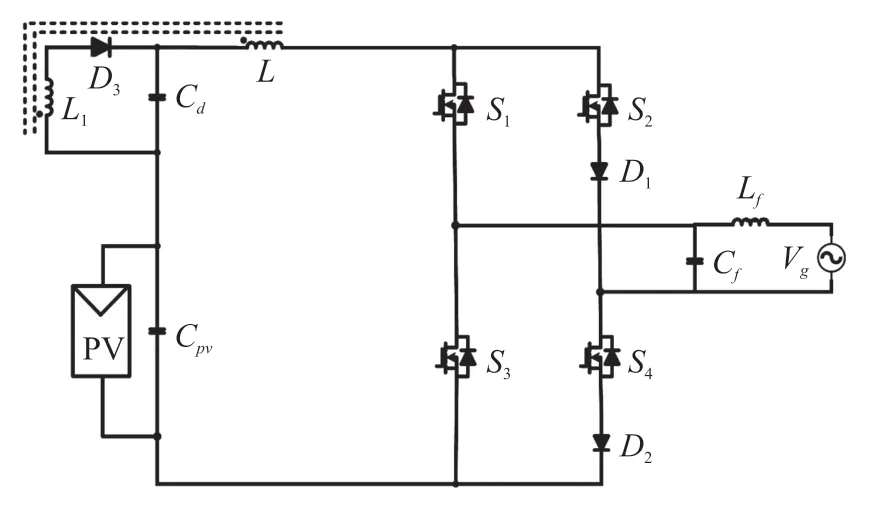
图2 所提光伏逆变器

所提电路工作在断续模式(DCM)，并在一个开关周期下分为四种工作模式。简言之，模式1，S1和S3导通，输入端口(包括PV 和解耦电容)为电感L供电。此时，能量转移至电感L。随后，基于电网极性，通过关闭S1(S3)，输入端和电感器L同时向电网释放能量。在下一个模式，通过关闭S3(S1)，电感L的剩余能量通过耦合电感L1和D3释放到解耦电容Cd。图3 和图4 分别为各工作模式的等效电路(Vg＞0)和逆变器的关键波形。此外，负半周期的等效电路和关键波形与正半周期的等效电路和关键波形相似，在此不再赘述。论文在模态分析之前做如下假设:

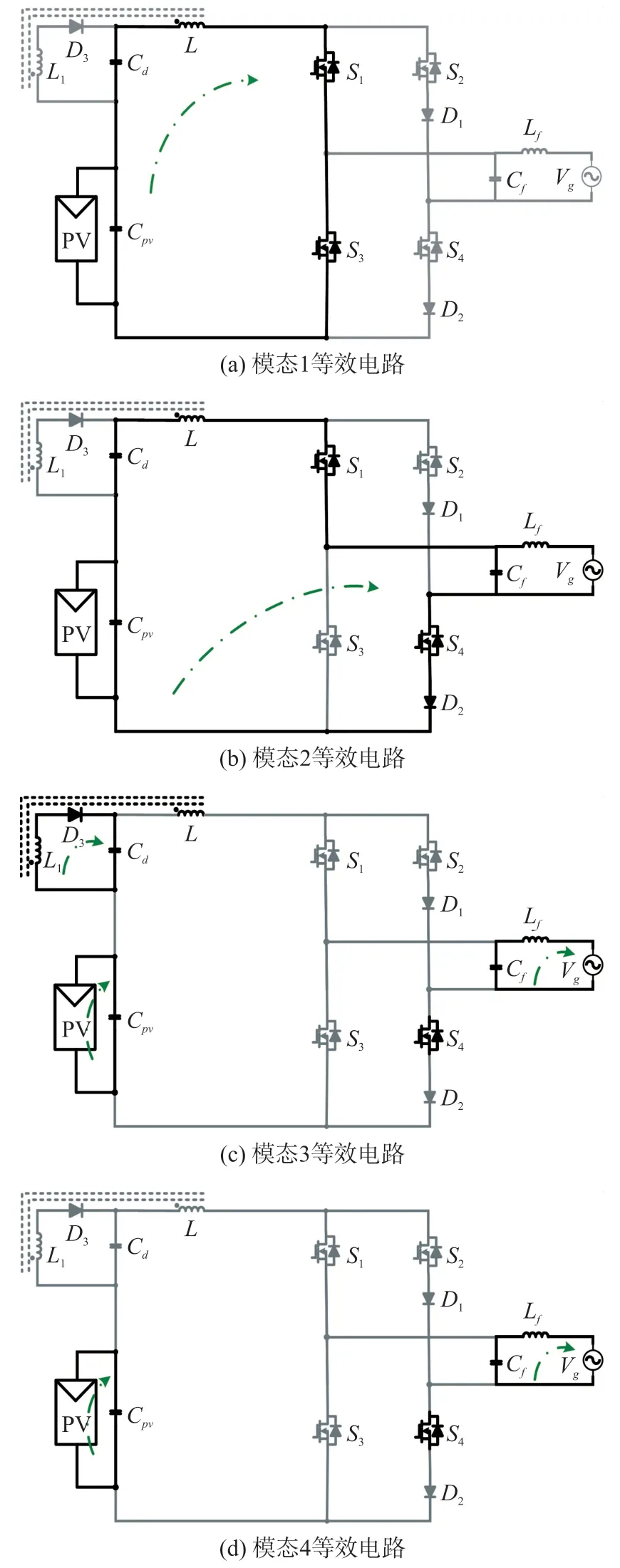
图3 不同模态的等效电路

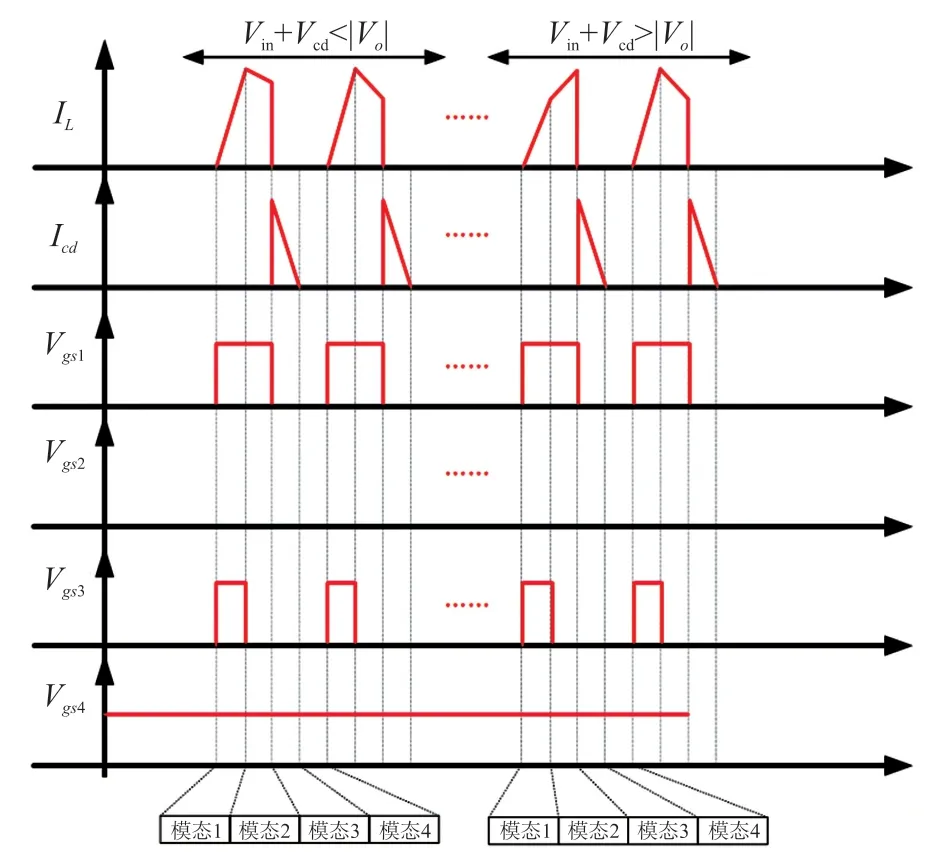
图4 所提变换器的关键波形

(1)开关频率远大于电网频率。因此，在每一个开关周期内，输出功率，输出电压和解耦电容两端电压可看做常量。

(2)开关管S3和S4工作在工频条件下以满足Vg正负极性交替。因此，仅正半周期被分析。

模态1 开关管S4导通，并保持整个正半周期开关状态不变，开关管S1和S3导通，输入电流从零线性上升到I1，等效电路如图3(a)所示。式(2)和式(3)分别为输入电流和该模式的持续时间。

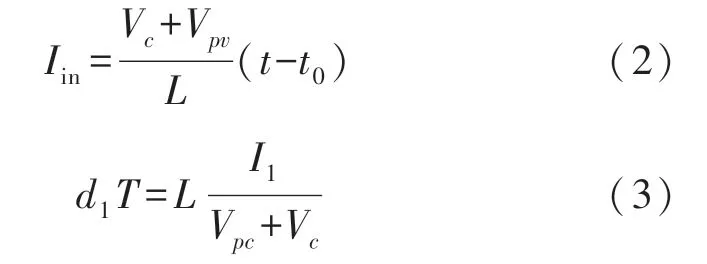
模态2 开关管S3断开，输入端和主电感L通过S1和S4同时向电网馈电，等效电路如图3(b)所示。此时，主电感电流根据电压极性线性增加或者减小。此阶段主电感电流可由式(4)表示，式(5)为此模态所需时间。

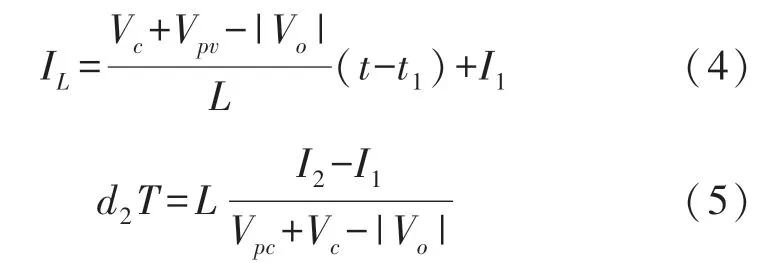
在模式1 和2，光伏板最大功率通过MPPT 算法传递至电网。在此模态下，输入电流平均值Iav必须等于最大特征点的光伏板电流。因此，

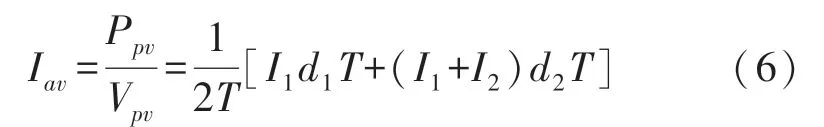
式中:I1和I2分别是模式1 和模式2 的电感L电流峰值。在模式2 结束时，电感器L中存储的功率为负载和输入功率之间的功率差。在模式1 结束时，电感峰值电流达到:

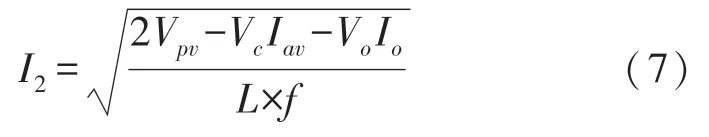
将式(3)、式(5)和式(7)代入为式(6)，可得

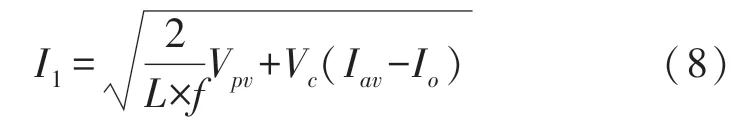
式中:Io为输出电流，其数学表达式为:

模态3 电感L中存储的能量通过耦合电感器L1和D3释放到解耦电容Cd，等效电路如图3(c)所示。此阶段结束时电感电流线性减少至零点。

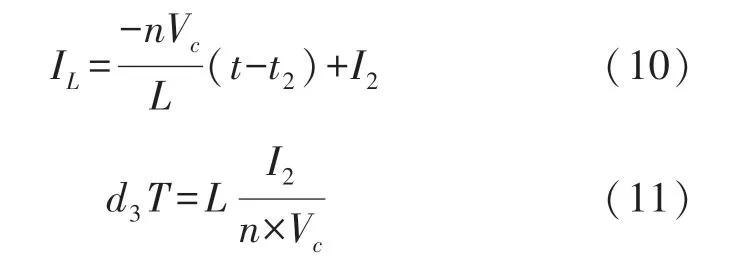
式中:n是为耦合电感匝数比。

模态4 主电感L中的电流为零。此时，电容滤波器提供输出功率，等效电路如图3(d)所示。

2 控制策略

所提控制策略的主要目标是从光伏侧提取最大功率，并馈电至电网侧。此过程由MPPT 算法完成，并控制开关S1～S4执行。由上述可知，MPPT 通过控制模式1 和2 中的开关S1和S3来实现。开关管S2和S4处于工频模式，并分别在负半周期和正半周期导通。

详言之，在模式1，开关S1和S3导通，输入电流线性增加以满足式(8)。在模式2，根据负载电压极性，将S1或S3关断，并通过S1，S4或S2，S3将适当功率输到网侧。MPPT 算法确定开关管S1和S3的占空比，以便满足式(3)和式(5)。最后，图5 给出了所提微型逆变器的控制策略，此外图中等式作为约束条件以满足系统稳定运行。

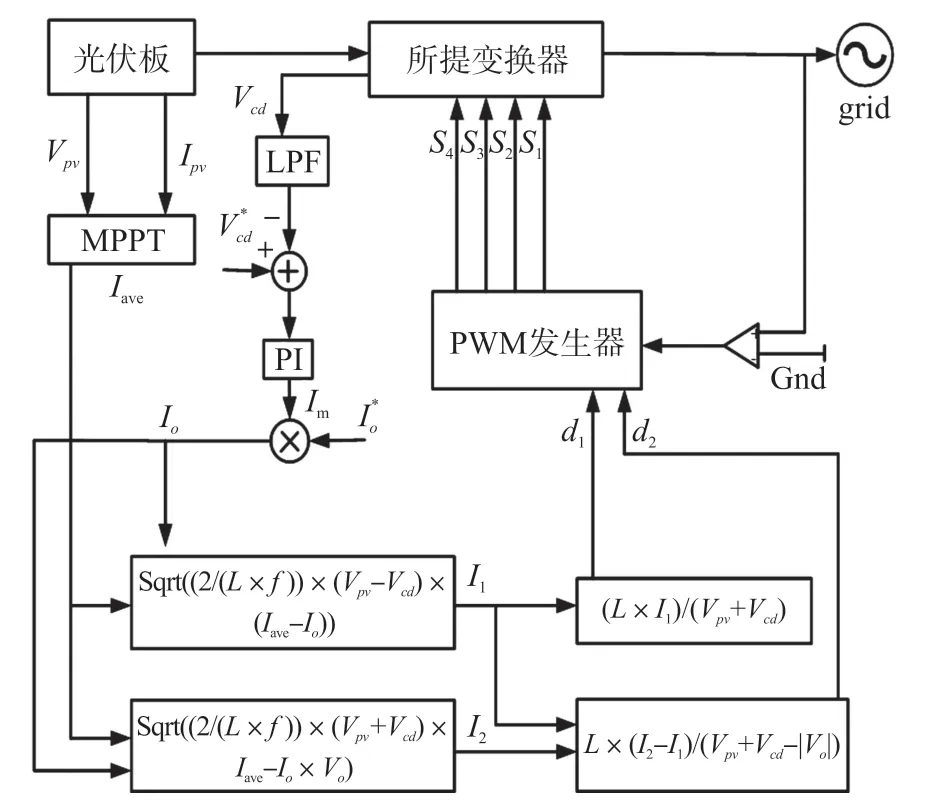
图5 微型逆变器的控制方案

3 设计考虑

由于所提变换器运行在断续模式，模式1 至3中的时间间隔之和必须满足下式:

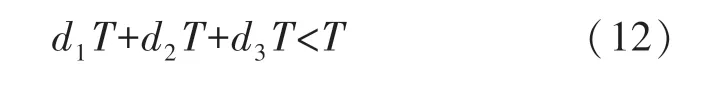
因此，根据式(3)，式(5)和式(11)，可得:

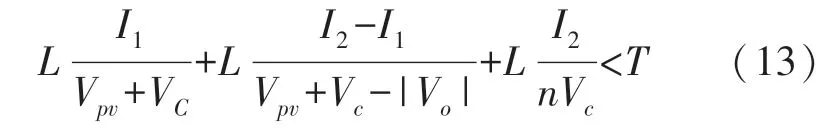
式中:I2和I1的值分别由(7)和(8)确定。

此外，二极管D3必须反向偏置，以防止在模式2 阶段能量流向解耦电容。因此，变压器T需满足下式:

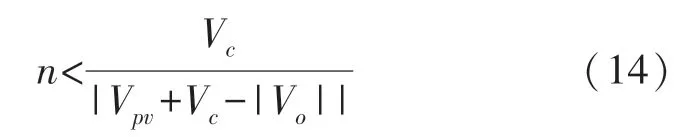
此外，主电感L和解耦电容Cd需分别满足式(13)和式(14)。

4 实验验证

为了验证理论分析的正确性及所提变换器的可行性，论文搭建了额定功率为100 W 的实验样机，如图6 所示。其中，主要实验参数如表1。

图6 实验样机

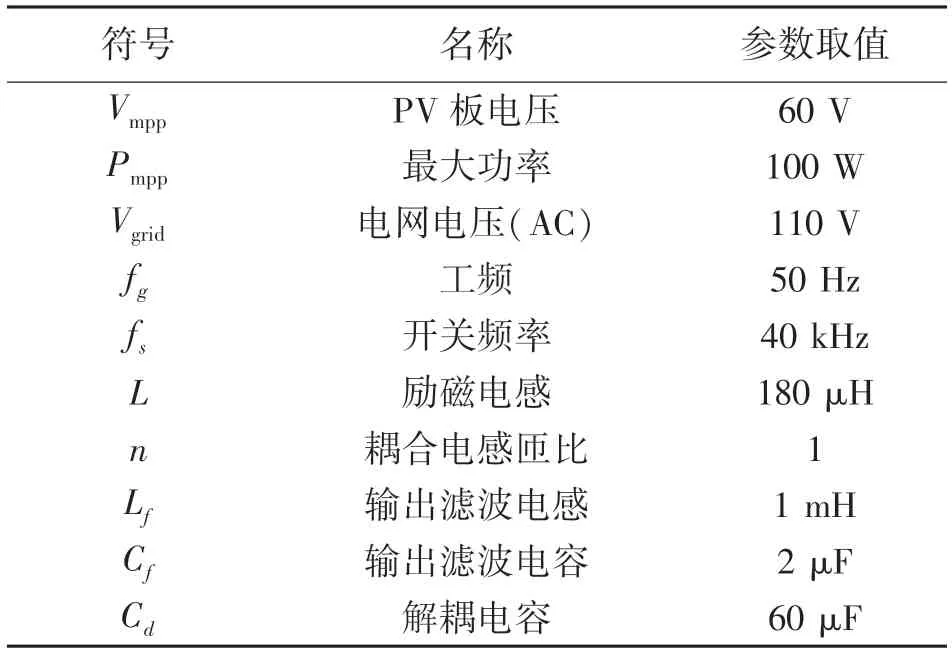
表1 仿真电路参数

图7 给出了该变换器在全载下输出电流Io的实验波形，可以看出，实验结果与稳态分析过程相符，近似正弦波，实测总谐波失真(THD)为1.38%。此时，样机效率高达91.5%。

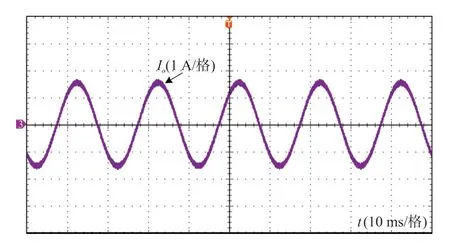
图7 逆变器输出电流

理论分析中，解耦电容在半个工频内充电、放电以补偿输入、输出造成的功率差。因此，解耦电容电压应表现为两倍于工频，且含有直流分量的波形。此外，所提逆变器的解耦电容由于与光伏板串接电压变化较大。基于式(1)分析，因此论文可采用较大纹波的薄膜电容代替电解电容。基于上述分析，图8 给出了解耦电容两端平均电压Vcd和电压纹波，其值分别为190 V 和50 V。

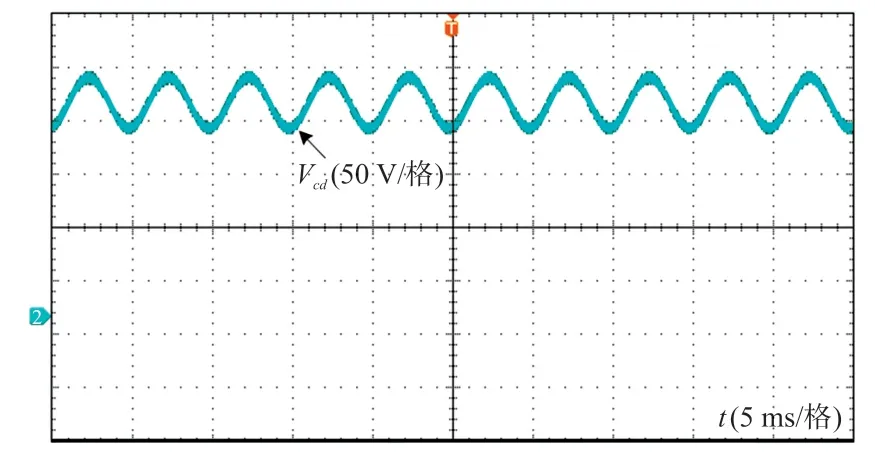
图8 解耦电容电压

图9 为输入电流，功率解耦电路电流和开关管S1，S2的触发脉冲。如图9 所示，在模态1 阶段，开关管S1和S3导通，输入电流运行在DCM，并且幅值从零线性增加至I1，其中I1辐值由MPPT 算法决定。然后，在模态2，开关管S1关断，电流注入电网，以满足式(8)要求。最后，存储在解耦电路中的剩余能量会通过耦合电感释放至解耦电容。此时主电流线性降低至零。此过程与式(7)理论分析相符。

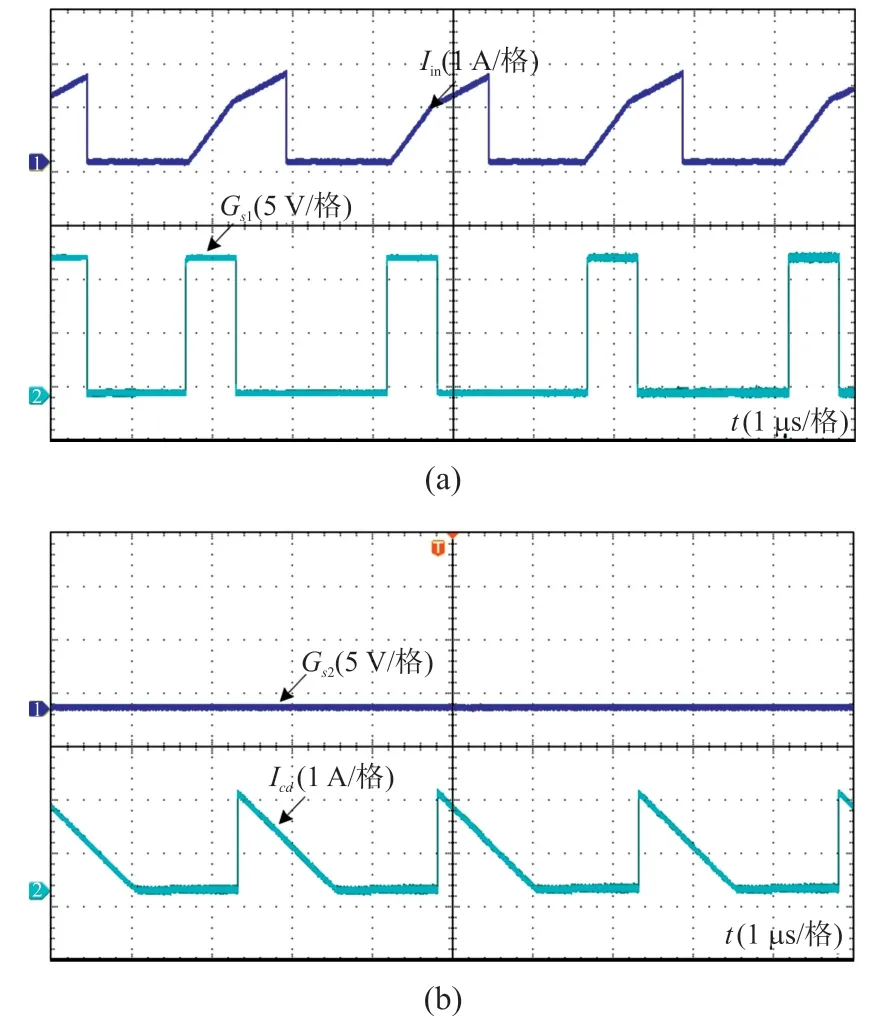
图9 输出电流，解耦电路电路和S1-2相应的触发脉冲(Vg＞0)

5 结论

本文提出一种基于反激电路的新型电流源型(CSI)串联功率解耦的方案。该逆变器在无需额外开关器件的前提下实现了无电解电容运行，即输入和输出的功率差值通过耦合电感释放至解耦电容。因此，解耦电容可承受较大电压纹波，为薄膜电容替换电解电容提供了可能。此外，简单的结构，较少的额外器件和简单的控制使所提出结构成为并网逆变器的合适选择。最后，搭建了100 W 实验样机验证了理论分析的有效性。实验结果表明，在全载运行下，样机效率为91.5%，THD 为1.38%。