氘核中子反应截面的法捷耶夫方程理论计算

李 琰，庞丹阳,*，陈文棣，陶 曦，续瑞瑞，葛智刚

(1.北京航空航天大学 物理学院，北京 10008；2.中国原子能科学研究院 核数据重点实验室，中国核数据中心，北京 102413)

三核子体系的结构及核反应是检验各种核力模型的试验场[1-2]，n+d三核子体系的全套中子反应截面也是重要的核数据。因此，对于三核子反应体系的结构和反应模型的理论研究在核物理基础研究和核应用方面都有重要的作用。

自20世纪60年代被提出以来，法捷耶夫方程已广泛应用于三体体系的结构和反应理论研究[3-4]。结合两体现实核力以及三体核力，法捷耶夫方程已成为描述n+d三核子体系核反应最精确的理论工具[5]。但我国在此方面的研究与国际先进水平尚存在较大的差距。目前，中国核数据中心CENDL数据库中d核中子反应数据的理论计算结果是20世纪八九十年代由中国原子能科学研究院的储连元等完成的[6]。这些计算所采用的核子-核子相互作用为s-波可分离势[7]。在中子入射能量小于20 MeV的区域，此相互作用对n+d全套中子反应数据的描述能力尚可。但随着中子入射能量的增加，s-波相互作用将越来越不足以对氘核中子反应截面数据提供精确的理论预测。为此，需要开展基于法捷耶夫方程的三体核反应理论研究，采用超出s-波的核子-核子相互作用的法捷耶夫方程的数值求解，实现对较高能量范围内的全套中子反应数据的准确预测。

本文主要介绍利用法捷耶夫方程计算n+d三核子反应体系的弹性散射微分截面、破裂反应、破裂反应出射中子和质子的双微分截面的理论框架及数值计算结果，同时计算弹性散射总截面和破裂反应总截面的激发函数。

1 三体核反应的法捷耶夫方程理论简介

本文考虑3个全同粒子在两体短程相互作用下的散射问题。对于n+d体系，分别用1、2、3表示这3个核子(通常取入射中子为粒子1，氘核中的中子和质子分别为粒子2和粒子3)，它们的质量为m，核子-核子相互作用势用va(α=1，2，3)表示。在动量空间，三体系统的波函数可用3套雅可比坐标(pα，qα)表示，分别对应3个道哈密顿量Hα(α=1，2，3)。

入射道(α=1)的道哈密顿量H1为：

(1)

三体系统的总哈密顿量(仅考虑两体核力)为：

H=H1+V1=H2+V2=H3+V3

(2)

其中，Vα=vβ+vγ，vα为粒子β、γ之间的两体相互作用(α，β，γ=1，2，3)。对于道哈密顿量Hα，反应道格林函数定义为：

(3)

对于n+d三核子体系，总能量E=Ecm+ε0，其中Ecm为质心系能量，ε0=-2.224 MeV为氘核的束缚能。

三体系统的弹性散射和破裂反应的跃迁算符U所满足的法捷耶夫方程[8-9]为：

U=Pv1+Pv1G1U

(4)

其中，P=P12P23+P13P23为粒子置换算符。

弹性散射振幅可用U算符的矩阵元表示为：

(5)

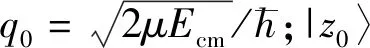
单道破裂反应振幅可用U算符的矩阵元表示为：

(6)

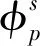
(7)

(8)

(9)

(10)

其中，(pi，qi)为反应道的雅可比动量(i=1, 2, 3)，它们之间具有简单的换算关系[11]：

(11)

(12)

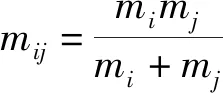
对于3个全同粒子体系的破裂反应，可只计算1个道的破裂反应振幅，如TΣs(p1,q1)，而其他道的破裂反应振幅可通过以上运动学关系计算得到。由破裂反应总振幅可得到破裂反应五微分截面：

(13)

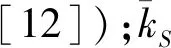
(14)

其中，klab为入射中子在实验室系的动量。破裂反应的双微分截面(破裂反应截面随某一出射粒子的能量和角度的变化关系)可通过对五微分截面的积分得到：

(15)

(16)

同样地，对双微分截面积分可得到破裂反应总截面(σbu)。但从数值计算的角度看，这样得到的破裂反应总截面难免存在较大的数值精度问题。在本文所关注的几十MeV的入射能量范围内，三核子反应体系只有弹性散射和破裂反应两个反应道，因此破裂反应总截面可通过总截面(σtot)和弹性散射总截面(σel)的差得到，即：

σbu=σtot-σel

(17)

而σtot可利用光学定理，由零度弹性散射振幅的虚部得到。从而避免了由对三体反应运动学的多重积分所带来的数值精度问题。

在采用一阶可分离势形式的s-波核子-核子相互作用的条件下，方程(4)形式的法捷耶夫方程可转化为以下积分方程[8]：

(18)

跃迁振幅F与U矩阵的关系为：

〈q,φs,ΣL|g0(E)U(E)g0(E)|q′,φs′,ΣL〉

(19)

其中：L为第3个粒子相对两体子系统的轨道角动量；g0(E)为自由的核子-核子相互作用体系的格林函数；φs为可分离势的形状因子。本文采用Yamaguchi形式的可分离势[10]：

νs=|φs〉λs〈φs|s=0, 1

(20)

(21)

在此相互作用下，两体体系的t矩阵也具有可分离的形式：

ts(E)=|φs〉τs〈φs|

(22)

(23)

值得注意的是，方程(18)中的τ函数对应的是三体系统中的两体t矩阵。本文所用的可分离势参数βs和λs来自文献[10]。

方程(18)中的Z函数对应两体有效相互作用。在上述一阶可分离势的条件下，其表达式为：

(24)

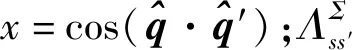
本文采用波包展开方法求解方程(18)形式的法捷耶夫方程[8]。n+d三核子体系的弹性散射和破裂反应振幅可由方程的解直接得到：

(25)

(26)

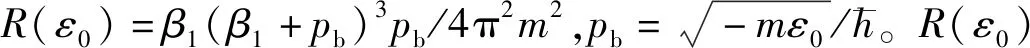
(27)

2 结果与讨论

n+d三核子体系弹性散射微分截面计算结果与实验数据的比较示于图1，其中Elab为中子入射能量，θc.m.为质心系角度，1 b=10-24cm2。利用上述Yamaguchi形式的一阶s-波可分离势求解方程(18)，得到的入射能在20 MeV以下的n+d体系的弹性散射如图1中蓝色线所示(实验数据来自文献[13-18])。与之对比的红色线是采用分离化的巴黎势(PEST16势)的计算结果[19]。除了s-波相互作用，PEST16势还包含p-波相互作用，并给出了氘核的d态成分，因此PEST16势应较Yamaguchi势能更好地描述n+d体系的核反应。与实验数据的比较也证实了这一点。但从图1也可看出，低能条件下n+d体系的弹性散射主要是由s-波相互作用贡献的，因此即使采用非常简单的两参数的Yamaguchi势，也可较好地描述入射能在20 MeV以下的弹性散射数据。

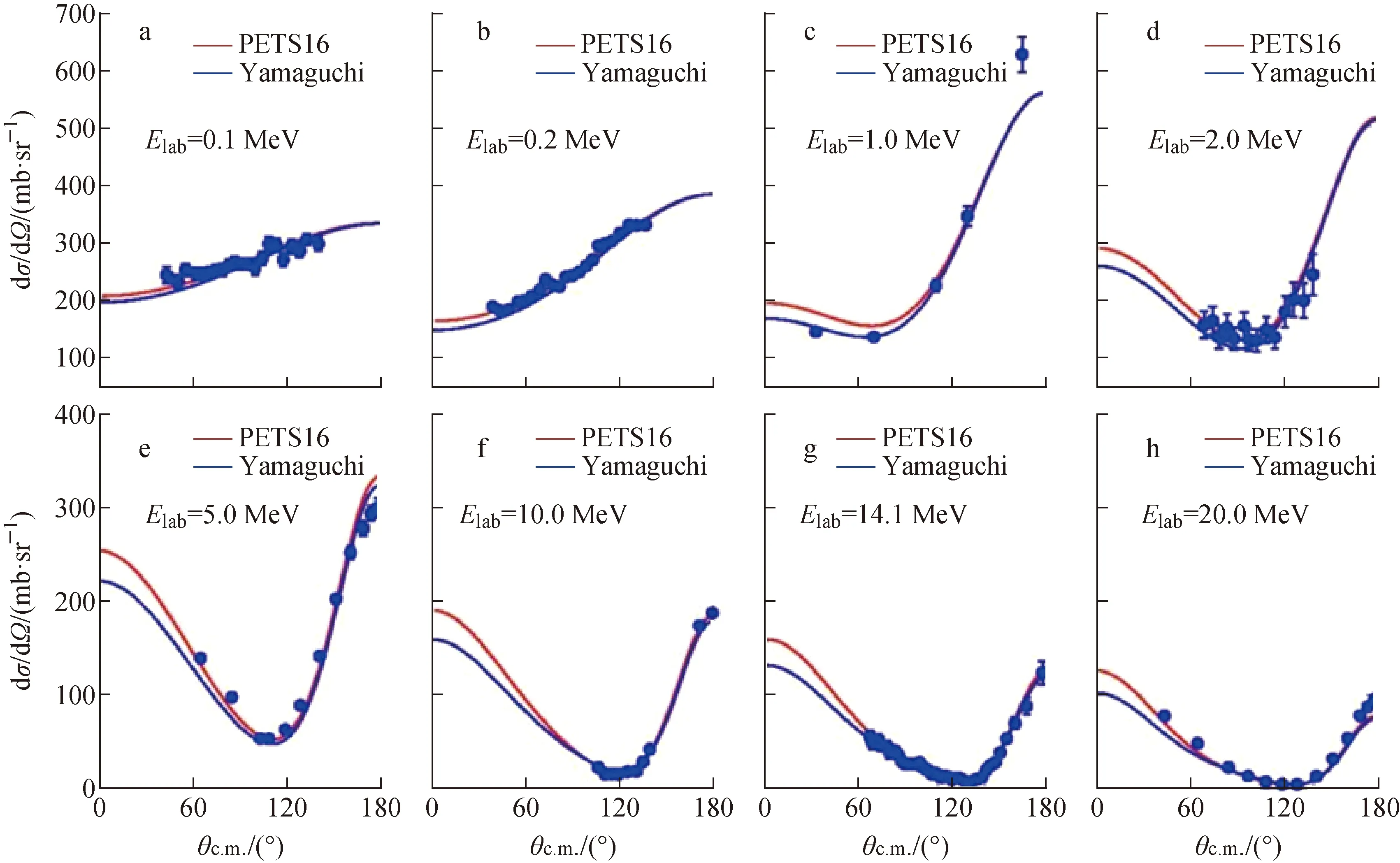
图1 n+d三核子体系弹性散射微分截面计算结果与实验数据的比较Fig.1 Comparisons between calculated results and experimental data of elastic scattering differential cross sections of n+d three nucleon system

图2为采用PEST16势计算的20 MeV以下入射能的弹性散射计算结果，及与ENDF/B-Ⅷ.0、CENDL-3.2、JENDL-5和JEFF-3.3库中评价数据的比较。ENDF/B-Ⅷ.0数据库采用R-矩阵分析结合三体相空间分布的办法。而CENDL-3.2、JENDL-5和JEFF-3.3则与本文相同，均通过求解法捷耶夫方程得到弹性散射截面。CENDL-3.2采用s-波可分离势，JENDL-5采用PEST16可分离势，JEFF-3.3采用的则是现实核力INOY。可看出，除JENDL-5在入射能小于约2 MeV的条件下与本工作及其他评价数据的结果有较明显的差别外，各组理论计算对于20 MeV入射能以下的弹性散射实验数据均可做出准确的描述。

最近，北京大学研究团队测量了入射能在13.56～52.48 MeV范围内的n+d弹性散射截面[20]。本工作采用Nijmegen现实核力[21]，通过求解法捷耶夫方程对其进行了理论分析，计算结果如图3所示。目前评价数据库中只有ENDF/B-Ⅷ.0和JENDL-5有此能量范围内的评价数据。从图3可看出，本工作的计算结果与JENDL-5求解法捷耶夫方程的结果几乎完全一致(实验数据来自文献[20，22-23])。图3b中，ENDF/B-Ⅷ.0评价数据库的结果更好地描述了27.5 MeV能量下的实验数据，但需要注意到它是基于R矩阵拟合，而非基于少体核反应理论计算的结果。

图3 本工作对入射能高于20 MeV条件下的n+d弹性散射角分布的计算结果与实验数据及ENDF/B-Ⅷ.0和JENDL-5库中评价数据的比较Fig.3 Comparison between results of this work calculations and n+d elastic scattering data at incident energy above 20 MeV and results in ENDF/B-Ⅷ.0 and JENDL-5 libraries

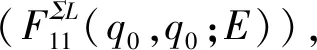
图4 n+d散射中出射中子和出射质子的双微分截面理论计算值与实验数据以及其他数据库的比较Fig.4 Results of calculations for double differential cross sections of emitting neutron and proton particles in n+d scattering and their comparisons with experimental data and other libraries

图5为n+d体系弹性散射总截面和破裂反应(d(n,2n)p反应)出射中子总截面的计算结果与实验数据以及ENDF/B-Ⅷ.0、CENDL-3.2、JENDL-5和JEFF-3.3库中评价数据的比较(实验数据来自文献[14,17,22,29-35])。在这些计算中，本工作计算采用PEST16两体相互作用。如前所述，利用光学定理得到总截面，从总截面中减去弹性散射总截面得到破裂反应出射中子总截面。可看到，本工作的计算结果整体符合实验数据。但与其他评价数据库中的结果在某些条件下存在一定的差异。这些差异的具体原因有待进一步研究。

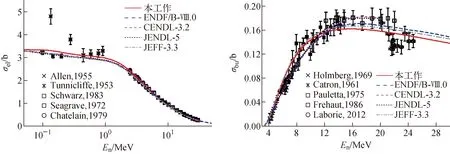
图5 本工作对弹性散射总截面σe1和(n,2n)破裂反应出射中子总截面σbu的计算结果与实验数据及ENDF/B-Ⅷ.0、CENDL-3.2、JENDL-5和JEFF-3.3库中评价数据的比较Fig.5 Comparisons among theoretical calculations for total elastic scattering cross section σe1 andd(n,2n)p reaction cross section σbu, experimental data, and results in other libraries

3 总结与展望

本文介绍了利用法捷耶夫方程方法计算氘核中子反应截面的理论框架、计算结果及其与实验数据和ENDF/B-Ⅷ.0、CENDL-3.2、JENDL-5、JEFF-3.3等数据库中评价数据的比较。对于弹性散射截面的计算，本工作实现了采用PEST16、Nijmegen等超出s-波相互作用的两体核力的法捷耶夫方程的求解，计算结果与实验数据符合良好，并可实现对入射能高于20 MeV条件下的弹性散射截面的准确预测。对于破裂反应，目前本工作仅实现了采用Yamaguchi形式的可分离化的s-波相互作用的法捷耶夫方程理论的计算。利用超出s-波相互作用对n+d三核子体系破裂反应截面的准确计算是未来研究的重点内容。