基于自适应虚拟同步发电机的直驱风电并网研究

2022-06-02刘建龙郝正航

电力科学与工程 2022年5期

刘建龙，郝正航，陈卓

（贵州大学电气工程学院，贵州贵阳 550025）

0 引言

近年来，可再生能源在全世界备受关注。风电因具有清洁、灵活、可再生的优点而被许多国家开拓使用[1]。

在电力系统中，可再生能源与电力电子设备应用比例的升高，对电力系统的平衡能力、电网的调节能力造成了负面影响，同时也使电网的故障形态更加复杂[2,3]。高比例电力电子设备的入网，导致电力系统的惯量呈现大幅度降低的形势[4,5]，这将使得现有的电网控制模式可能失效，电网的安全稳定运行存在巨大的隐患。为此，国内外学者针对电力系统的惯量阻尼进行一系列的研究。

VSG技术借鉴了同步发电机的电磁与机械方程[6]，从运行机理和外特性上等效同步发电机模型，可为逆变器提供惯量、阻尼等支撑[7]。文献[8,9]研究了VSG参与电网低频振荡控制的原理以及对各控制环节产生的影响，推导了转动惯量和阻尼系数在低频段的约束条件。文献[10]提出了以虚拟功角和频率作为宏变量的VSG暂态稳定协同控制来改善系统稳定性。文献[11]研究发现线路电感会对系统产生负阻尼，因此通过虚拟阻抗控制方法来补偿电感阻尼分量以抑制功率振荡。文献[12]在传统VSG控制前向通道和阻尼反馈通道增加微分校正环节，通过改变其动静态特性来满足不同频段的控制品质需求。文献[13,14]针对VSG的旋转惯量自适应进行研究，根据负载变动而导致频率出现的偏差量和变化率来调节旋转惯量大小；但该研究对象较为单一。文献[15,16]对转动惯量和阻尼系数采用划分区域的判断方法来确定其值，其过程较为繁琐且缺乏灵活性。文献[17]以转子角频率的变化率作为约束条件，建立了转动惯量和阻尼系数的自适应方程；但研究中并未考虑频率偏差量的影响。文献[18]根据转子频率的变化设计了惯量阻尼的自适应控制方法，但文献未给出相应调节系数的选取原则。

在系统功频发生波动时，传统固定转动惯量和阻尼系数的VSG控制方法因惯量阻尼固定而无法实现实时最优调整，导致系统动态响应慢以及稳定性低。

针对上述问题，本文提出了一种改善VSG惯量阻尼的方法，即根据转子角速度的变化率和偏移量来实时调整固定的惯量阻尼以达到自适应的目的。

1 VSG基本结构

VSG由3部分构成，包括：功率计算单元、虚拟功频与励磁控制器单元、参考方程单元。

VSG控制系统结构框图如图1所示。

图1 VSG控制系统结构框图Fig. 1 Block diagram of the VSG control system structure

图1中：R0、L0为逆变器输出侧电阻、电感；Rf、Cf为滤波电阻、电容；Rg、Lg为电网侧电阻、电感；Pref、Qref为给定有功、无功功率。

2 固定惯量阻尼VSG控制策略

2.1 虚拟功频控制器

维持系统频率稳定是保证电力系统稳定运行的关键。系统有功的变化，会对系统频率产生很大的影响。为了维持系统频率的稳定，在系统有功功率变化时，功频控制器通过角速度差值来对虚拟机械功率进行调节，使系统有功处于平衡状态。这一控制过程模仿了同步发电机的转子运动过程，数学模型为：

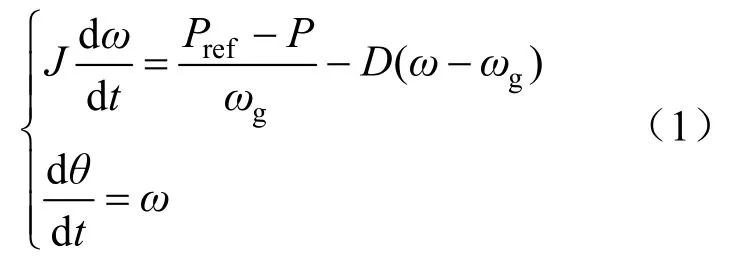
式中：J为旋转惯量；D为阻尼系数；Pref为有功给定值；P、ω为VSG的输出功率和角速度；ωg为电网额定角速度；θ为虚拟功角。

由P-f下垂特性可知：

式中：Kp为下垂系数；τ为一阶滤波器的滤波参数。

由式（1）和式（2）即可构成虚拟功频控制器，其相应控制框图如图2所示。

图2 虚拟功频控制器控制原理框图Fig. 2 Block diagram of control principles of the virtual power frequency controller

2.2 虚拟励磁控制器

系统无功的变动可能导致电压的升高或降低，因此可通过对电压的调节使系统无功达到平衡。同步发电机通过调压方程来对电压进行调节，其方程为：

式中：E0为空载电动势；Uref为给定电压值；Ku为积分系数；s为积分算子。

由Q-U下垂特性可知：

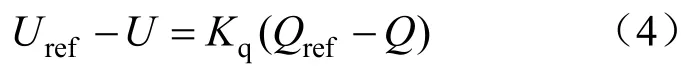
式中：Kq为下垂系数；Qref为给定无功值。

将式（4）代入到（3）中，可得输出的虚拟电动势方程为：

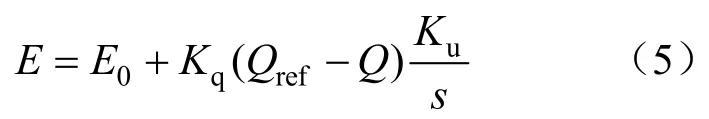
由式（5）可构成虚拟励磁控制器，其相应控制框图如图3所示。

图3 虚拟励磁控制器控制框图Fig. 3 Block diagram of the virtual excitation controller control

2.3 VSG参考方程

由式（1）和式（5）可合成VSG的参考电压Vabc，其方程为：

VSG逆变器控制策略中，电压电流双闭环控制的给定参考电压即为Vabc。

3 自适应惯量阻尼VSG控制策略

3.1 J、D对有功功率的影响

由隐极式发电机的功角特性曲线可知，发电机输出的有功可表示为：

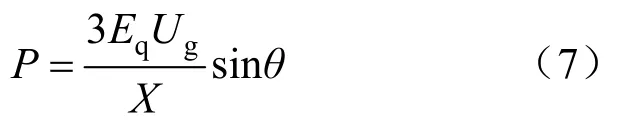
式中：Ug为电网电压；X为发电机电抗；Eq为发电机感应电势；θ为功角。

对式（1）和式（7）进行线性化处理以及拉氏变换，可得VSG有功小信号数学模型为：

由式（8）可得VSG有功环的小信号结构，如图4所示。

图4 VSG有功功率小信号结构框图Fig. 4 Block diagram of the VSG active power small signal structure

在研究有功功率环时，除自身输入信号外的其它信号均视为扰动。由图4可推导出有功功率环路增益为：

当有功环路出现负反馈时，系统逐渐会达到一个稳定的工作点，此时可等效为二阶系统，则闭环传递函数为：

将式（9）代入式（10）可得：

将式（11）与二阶标准型系统的传递函数相比较，可以得出：

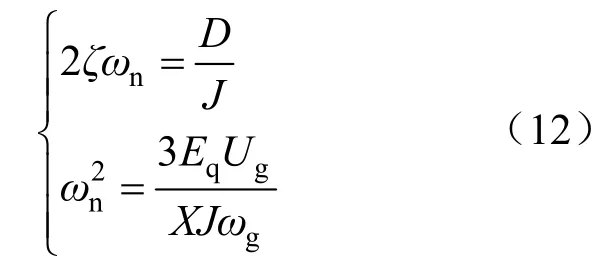
将式（12）的方程组联立求解，可得：

阻尼比ζ的值决定了系统的动态过程。期望ζ∈(0,1)，这样系统将会呈现出一个振荡衰减的响应过程。

由式（13）可知，当D固定时，ζ越大则J越小；当J固定时，ζ越大则D越大；当ζ固定时，D越大则J越大。因此可以得到J、D与ζ三者之间的关系，如图5所示。

图5 不同J、D的阻尼比分布图Fig. 5 Damping distribution diagram of different J and D

在欠阻尼的二阶系统中，可用阻尼比ζ和无阻尼自然振荡频率ωn来表示系统的超调量σ、调节时间ts等参数。当误差带为±5%，系统的ts和σ可简化为：

将式（13）代入式（14）中，可得由J、D来描述调节时间ts和超调量σ的方程为：

由式（15）可知，当D固定时，系统输出有功曲线的调节时间和超调量都随着J增大而增大，反之亦然。当J固定时，系统输出有功曲线的调节时间和超调量都随着D增大而减小，反之亦然。该结果如图6与图7所示。

图6 不同J下的有功输出特性Fig. 6 Active output characteristics under different J

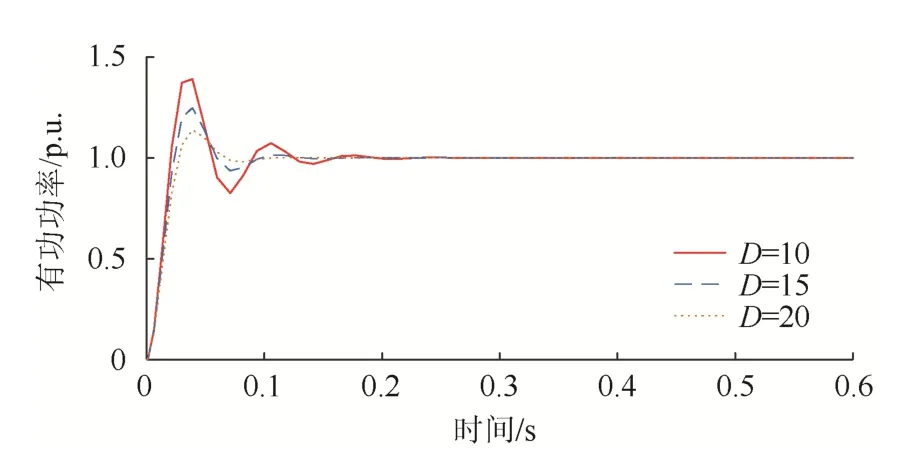
图7 不同D下的有功输出特性Fig. 7 Active power output characteristics under different D

3.2 J、D对频率的影响

根据式（1）可得：

由式（16）可知，当[(Pref–P)/ωg] –[Jdω/dt]固定时，转子角速度的偏移量Δω与D呈反比关系：D增大，Δω减小；D减小，Δω增大。当[(Pref–P)/ωg]–DΔω固定时，转子角速度的变化率dω/dt与J仍然呈反比关系：J增大，dω/dt减小；J减小，dω/dt增大。

因此，可通过实时调整转动惯量J和阻尼系数D来确保系统频率始终处于稳定的状态。

3.3 自适应VSG改进原理

由式（15）和式（16）可知，不同的转动惯量和阻尼系数对系统有功和频率的影响也相应不同。因此当外界扰动引起系统功频发生变化时，可通过实时在线调整转动惯量和阻尼系数的值，来改善有功频率特性。

针对该问题，结合功角特性和转子角速度振荡曲线，提出一种自适应惯量阻尼VSG协同控制策略，改进原理如图8～9所示。

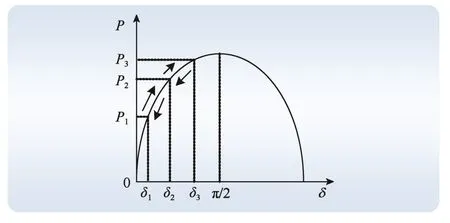
图8 功角特性曲线Fig. 8 Curve of power angle characteristics

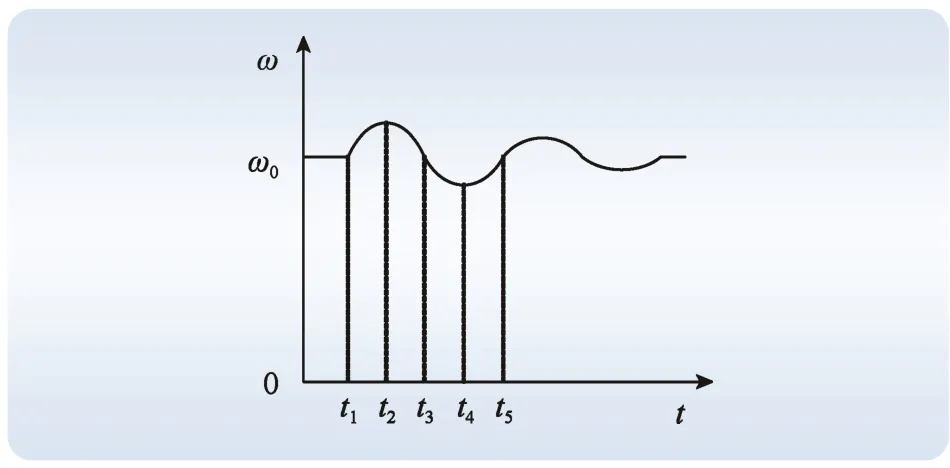
图9 转子角速度振荡曲线Fig. 9 Curve of rotor angular velocity oscillation

由图8和图9可知，一个振荡周期可分4个区间[t1，t2]、[t2，t3]、[t3，t4]、[t4，t5]。

在区间[t1，t2]，系统功率增加，ω>ω0且dω/dt>0，ω单调递增。此时应该增大J和D，用以减缓dω/dt和ω增加。

在区间[t2，t3]，ω>ω0且 dω/dt<0，ω单调递减，功角仍然处于上升阶段。此时应该减小J来增大dω/dt，同时增大D来减缓ω增加。

在区间[t3，t4]，ω<ω0且 dω/dt<0，ω单调递减。此时应该增大J和D，以此来减小dω/dt，约束ω下降。

在区间[t4，t5]，ω<ω0且 dω/dt>0，ω单调递增，功角仍然处于下降阶段。此时应该减小J且增大D来减缓ω下降。

根据上述原理，利用转子角速度偏移量 Δω和变化率dω/dt不同的变化情况来对J和D进行选取，选取规则如表1所示。

表1 J、D选取Tab. 1 Selection of J and D

根据表1的选取原则，可得自适应J、D的表达式为：

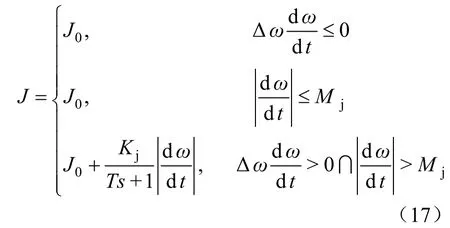
式中：J0为转动惯量初始值；Kj为转动惯量的调节系数；Mj为dω/dt的变化阈值。

式中：D0为阻尼系数初始值；Kd为阻尼的调节系数；Md为Δω的变化阈值。

由上述原理可知，自适应VSG改进控制能对转动惯量进行调节，同时通过对阻尼系数建立自适应方程，使系统受外界扰动时，惯量阻尼能够协同进行自适应调节控制，从而加快系统响应过程，提高稳定性。另外，在自适应转动惯量中引入惯性环节，能够使其过渡状态更加平滑。

4 自适应VSG调节系数整定

4.1 自适应阻尼的调节系数整定

将式（2）进行拉普拉斯反变换，可得：

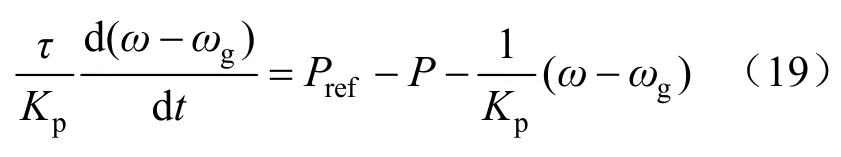
将式（1）改写为：

将式（19）与式（20）对比可得：

对式（21）进行简化可得：

由式（18）与式（22）联立可得：

令D0为10，Δω的阈值Md为±0.2，滤波参数τ为0.01。当输出J取0.4 kg·m2时，由式（23）可得：

对式（24）求解，可得Kd的取值范围为：

在实际应用中，应根据需求选取适当的阻尼调节系数Kd值。

4.2 自适应转动惯量的调节系数整定

由式（17）与式（22）联立可得：

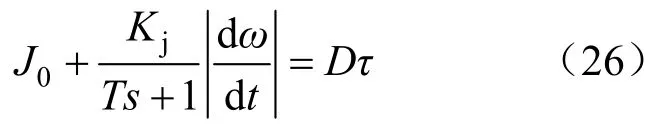
式（26）中的惯性环节能起到一定的滤波作用，从而保证了系统的过渡过程更加平滑。令滤波参数T为0.1，将式（26）改写如下：

令J0为 0.2 kg·m2，dω/dt的阈值Mj为±2.5。当输出D取30时，由式（27）可得：

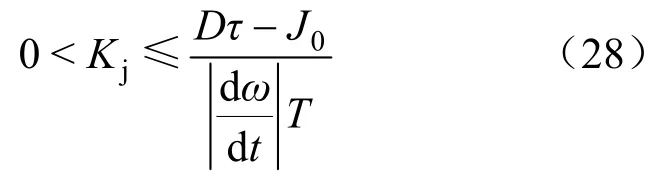
对式（28）求解，可得Kj的取值范围为：

在实际应用中，转动惯量的调节系数Kj也应根据需求进行适当选取。

5 仿真分析

为了验证自适应 VSG策略控制效果，利用MATLAB/Simulink搭建如图10所示的直驱风电并网控制系统模型。仿真步长为5×10–6s，仿真时长为1.4 s。并网系统主要仿真参数，如表2所示。

图10 自适应VSG风电并网仿真模型Fig. 10 Simulation model of adaptive VSG wind power grid connection

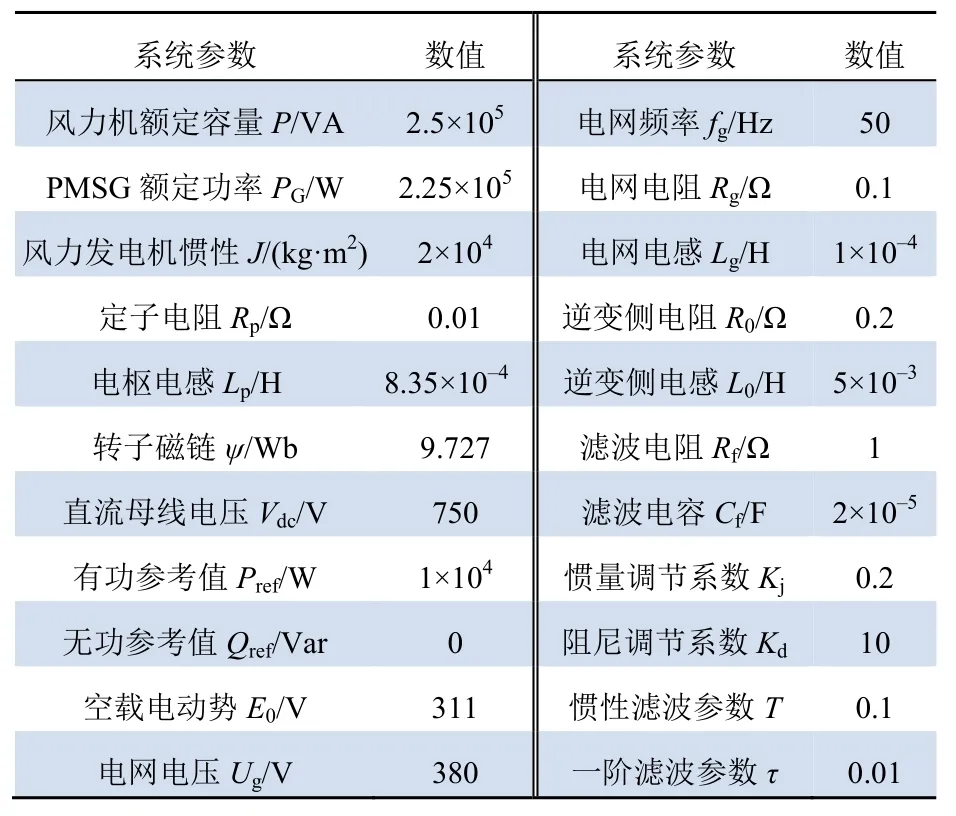
表2 系统主要仿真参数Tab. 2 The main simulation parameters of the system

5.1 调节系数对有功频率的影响

自适应 VSG控制系统的调节系数若发生变化，将会引起转动惯量和阻尼系数也发生相应变化。由图6和图7可知，不同惯量和阻尼将会导致系统的超调量以及调节时间发生明显的变化；以此来改变系统的性能，则选取合适的调节系数非常关键。

5.1.1 阻尼调节系数Kd对有功频率的影响

为了验证Kd变化对系统有功频率的影响，仿真时取Kd分别为5、10和30。仿真结果如图11与图12所示。

图11 不同Kd下的有功功率对比Fig. 11 Comparison of active power under different Kd

图12 不同Kd下的频率对比Fig. 12 Frequency comparison under different Kd

由图11和图12可知，不同的Kd值对系统的影响比较大：随着Kd取值不断增大，系统功频曲线的超调量显著减小，但调节时间却大幅度提高。这不利于系统高质量稳定运行。

5.1.2 转动惯量调节系数Kj对有功频率的影响

为了验证Kj对系统有功频率的影响，仿真时取Kj分别为0.1、0.2和0.4。仿真结果如图13与图14所示。

图13 不同Kj下的有功功率对比Fig. 13 Comparison of active power under different Kj

图14 不同Kj下的频率对比Fig. 14 Frequency comparison under different Kj

由图13和图14可知，不同的Kj值对系统的影响也各有差异。随着Kj取值不断增大，系统功频曲线的超调量也相应减小，调节时间却有所提高。由此可知，为转动惯量和阻尼选取合适的调节系数极为关键。

5.2 自适应惯量阻尼VSG控制的仿真结果

仿真条件：在0 s时，系统负荷给定的有功初始值为10 kW；在0.6 s时，突然增加了有功负荷5 kW；在1 s时，又降为10 kW。

图15～16是系统输出仿真计算结果对比图。由图可知，采用固定的J、D时，VSG输出频率和有功均存在较大的超调量，如频率的最大偏差达到了0.3 Hz，有功的最大偏差达到了900 W等，调节时间大约为0.3 s。但是，当系统采用自适应J、D时，VSG输出频率和有功的超调量大幅度降低，调节时间也略有降低但不明显；其中频率的最大偏差降低到 0.18 Hz，有功的最大偏差降低到100 W。由此可见，自适应J、D对VSG输出功率和频率的波动有一定的抑制作用。

图15 VSG输出频率Fig. 15 VSG output frequency

图16 VSG输出有功功率Fig. 16 VSG output active power

图17～18为电网侧频率和电流仿真结果对比图。由图可见，采用固定J、D时，电网侧的频率最大偏差达到了0.015 Hz，电流最大偏差达到了3 A，对应的电流总谐波畸变率（total harmonic distortion，THD）为1.54%，调节时间约为0.2 s。当采用自适应J、D时，电网侧频率最大偏差下降到0.01 Hz，电流最大偏差下降到0.5 A；此时的THD下降为1.44%，调节时间也略有降低但不明显。可见，自适应J、D对电网侧频率和电流的波动也有一定的抑制作用。

图17 电网侧频率Fig. 17 Grid-side frequency

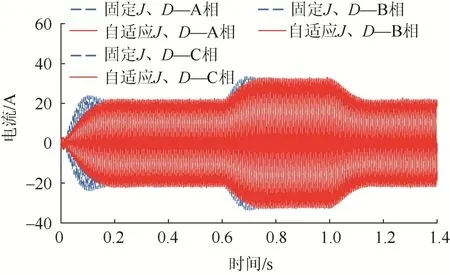
图18 电网侧电流Fig. 18 Grid side current

图19～20为系统分别采用固定和自适应J、D控制方式时，J和D的自身对比图。由图可知，系统在0 s、0.6 s时增大负荷、1 s时切除负荷情况下，此时J、D均处于协同自适应的状态，通过适当的调整J、D来减小频率波动的变化率以及偏移量，最终使得系统的超调量、调节时间大幅度降低减小，从而提高了系统的响应过程。