基于PSO-VMD算法的生命探测方法研究

陆 鑫，陈志敏,2

(1.上海电机学院 电子信息学院，上海 201306；2.东南大学 毫米波国家重点实验室，南京 210096)

0 引言

生命探测雷达是现代雷达技术和生物医学工程技术结合的产物，生命探测雷达在军事反恐、灾难营救、医疗检测等领域有广泛应用[1-3]，在航空航天领域也扮演重要的角色[4-5]。探测雷达通过电磁波穿透非金属遮挡介质等障碍物，探测到人体的生命特征，如呼吸、心跳、肢体动作等,通过处理雷达回波信号，可以实现对飞行员的呼吸心跳的监测。

雷达接收机接收到的回波信号除了含有生命体的特征信号，还包括非金属介质反射的强回波，以及周围环境带来的干扰和噪声。另一方面雷达接收信号具有非平稳、随机性强等特点，从中提取微弱的生命信号非常困难。其次，雷达接收信号经预处理，再经A/D转换后数据量较大，难以满足现场实时、快速探测的需求。因此，现有的生命探测雷达仍存在许多技术难点需要解决。

首先，针对回波信号具有非平稳性、非周期性和随机性强等特点，可以采用卡尔曼滤波法、小波变换、经验模态分解(empirical mode decomposition，EMD)和变分模态分解(variationalmode decomposition，VMD)等方法来处理。其中，卡尔曼滤波以最小均方误差为最佳估计准则来寻求递推估计的算法，能够对时变系统、非平稳信号、多维信号进行处理，但当噪声为统计特性未知的有色噪声或系统具有不确定性时，该方法会造成极大的误差[6]；小波变换通过多尺度分析把信号分解为不同的频率分量，但存在小波基函数的选择问题，适应性较差[7]；而EMD算法在分解时会因循环递归迭代产生混叠，且分解的层数是随机的，进行分解时无法手动确定不同模态的频率范围，缺乏理论上的证明，存在端点效应问题[8-10]。

VMD作为一种新的自适应信号处理方法，运算效率高，可克服EMD中的模态混叠问题，实现信号的准确分离，利用其自身具有的维纳滤波特性可获得更优的噪声滤除效果。该算法重点在于如何确定固有模态分量(intrinsic mode function，IMF)的分解层数k和惩罚因子α的个数。若k值过小会产生模态混叠，过大会导致过度分解；若惩罚因子α取值过大，则会造成分解的模态函数频带过窄，丢失有用信息，反之，会造成频带过宽而携带干扰信息。针对该问题，本文提出一种基于包络熵的粒子群(particle swarm optimization，PSO)算法对VMD算法进行改进以确定上述两个参数，实现提取雷达接收机回波信号中生命特征的目的。

本文核心内容主要包括4部分，第1部分给出了生命探测雷达的系统模型；第2部分提出一种基于包络熵的PSO-VMD生命探测算法，并给出算法的具体实现；第3部分对本文所提出的算法进行实验验证和仿真对比分析；第4部分主要是对本文工作的总结。

1 生命探测雷达回波信号建模

由于超宽带微功率脉冲雷达穿透能力强，抗干扰能力强，探测灵敏度高，能探测呼吸和体动等微弱的生命特征，因此被广泛应用于生命探测领域研究[11]。本文采用超宽带雷达体制对生命信号进行研究，重点关注人体生命信号的探测和辨识，不考虑人员的定位和数量。考虑到人体呼吸和心跳引起的胸腔运动具有一定的周期性，可以用单频正弦信号来近似表示。为简化分析，假设呼吸心跳引起的胸腔振动是等距离振动，即只需要考虑呼吸心跳的频率特征，则呼吸心跳引起的胸腔振动模型Z(t)可表示为：

Z(t)=Arsin(2πf1t+φ1)+Ahsin(2πf2t+φ2)

(1)

其中，Ar、Ah分别为人体呼吸和心跳引起的胸腔和脉搏运动幅度，f1、f2分别为呼吸和心跳的频率，φ1、φ2分别为呼吸和心跳的初始相位。

对于频率为fc的电磁波，将生命探测雷达与飞行器内各种障碍目标之间的距离记为Rn(n=1,2,…,N)，雷达与飞行员之间的距离记为R0，那么来自障碍物以及飞行员的回波信号可以表示为：

(2)

其中，An表示第n个目标回波信号的幅度，fc为载波频率，B表示飞行员回波幅度，Z(t)表示飞行员引起的胸腔距离变化。

那么，叠加噪声后得到雷达回波信号R(t)为：

(3)

最终，根据式(3)，我们需要从得到的回波信号中，提取呼吸和心跳的频率。接下来提出一种基于PSO-VMD的生命探测算法对接收信号进行处理。

2 基于PSO-VMD的生命探测算法

2.1 信号预处理

生命探测雷达回波中包含了强背景噪声与杂波等干扰，为消除干扰影响，有效提取生命体征信号，需要对接收信号进行预处理[13-15]，具体如下：

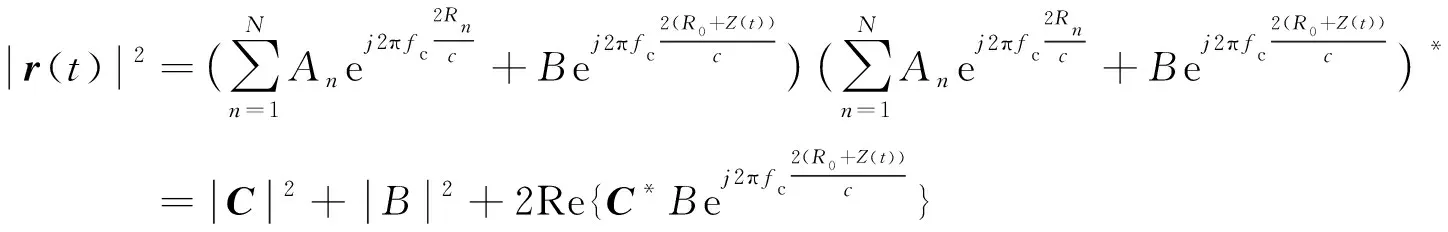
(4)

2.2 PSO-VMD重构雷达回波信号

在VMD的分解过程中，若分解层数k取值过大，则会造成过度分解，出现虚假模态；反之，会导致分解不充分，产生模态混叠。同时，若惩罚因子α取值过大，则会造成分解的模态函数频带过窄，丢失有用信息；反之，会造成频带过宽，携带干扰信息。对此，本文采用粒子群算法选择包络熵作为适应度函数，来确定以上两个参数的最优组合，达到改进VMD算法的目的。

2.2.1 VMD算法

VMD是一种新的自适应信号处理方法，对非线性、非平稳信号的处理具有明显的优势。该方法运算效率高，利用迭代搜索变分模型最优解确定每个分解的分量中心频率及带宽。VMD算法可以抑制大部分的噪声，有效降低信号的非平稳性，并将生命体征信号分解为一系列的IMF分量。

VMD算法的实现核心主要分为构造变分问题和求解变分模型2个步骤[16-17]，具体如下。

1)构造变分问题

VMD算法是将原始信号f(t)分解为k个具有特定稀疏性的相互独立的固有模态函数。首先，对uk(t)进行希尔伯特变换，得到分解信号的单边频谱[(δ(t)+j/πt)uk(t)]。随后引入e-jωkt对每一个模态中心频率进行调整，实现将频谱调制到基带。最后，计算每个解调信号梯度的平方L2范数，估算uk(t)宽度。受约束的变分问题可描述为：

(5)

式中：δ(t)为狄利克来函数；uk，ωk分别为IMF具有有限带宽的模态分量和中心频率；f(t)为原始信号。

2)求解变分模型问题

通过引入惩罚因子α和拉格朗日乘法算子λ，将约束性变分问题变为非约束性变分问题。增广拉格朗日表达式为：

(6)

最优解采用二次惩罚和拉格朗日乘数将上诉约束问题转换为非约束问题，并用交替方向乘子法(alternating direction method of multipliers，ADMM)求解这个非约束问题，通过迭代更新最终得到信号分解的所有模态。分解的所有模态中有包含主要信号的模态和包含噪声的模态。

2.2.2 PSO算法

本文采用粒子群优化算法来确定VMD的惩罚因子α和分解层数k。粒子群算法是一种智能优化算法，相比于其他算法，搜索速度快、算法简单、效率高。通过粒子状态初始化，不断寻优和迭代比较个体最优和全局最优来调整粒子对环境的适应度，搜索到最优的区域的最优解，PSO算法具体描述如下：

对于一个D维空间存在n个粒子组成的种群X，其中第i个粒子以速度为Vi=(vi1,vi2,…,viD)飞行，粒子在空间的位置为Xi=(xi1,xi2,…,xiD)，粒子的最佳位置记为pi=(pi1,pi2,…,piD)。其种群的最佳位置为pg=(pg1,pg2,…,pgD)。作为它的第d+1维的速度Vid+1与位置Xid+1的更新表达式为：

(7)

其中，vid为粒子速度：i∈[1,n]；d+1∈[1,D]，c1与c2为加速常数，ω为惯性权重，r1，r2是0到1的任意随机数。为了确保搜索准确，跳出局部获取全局的最优解，要将粒子的速度与位置控制在一定的范围内。

2.2.3 包络熵

VMD算法虽然避免了EMD算法存在的模态混叠和端点效应问题，但由于VMD算法中的惩罚因子α和分解层数k是未给定的参数，而两个参数的选择又对VMD分解的影响很大。由于两个参数一般是依靠人们的经验确定，缺乏严格的证明，因此制约了VMD算法在各种工程中的应用。信号的熵值反映了它的随机程度和复杂程度，信号的周期性越明显，复杂程度越低，熵值越小，反之非周期性噪声干扰越多，信号越复杂，熵值越大[18]。因此本文采用包络熵作为粒子群算法的适应度函数。生命信号经过VMD算法分解后的IMF分量的包络熵可表示为：

(8)

式中，i为原信号分解得到的IMF层数；pi,j为ai(j)的归一化形式；ai(j)为信号IMF经希尔伯特变换后得到的包络信号。当信号经VMD分解得到IMF分量包含的周期性生命体征信号越多，包络熵较小；反之，周期性信号越少越稀疏，包络熵值则越大。因此，为了得到周期性较好的生命体征信号，本文采用包络熵的最小值作为PSO算法适应度函数的判别方式。

2.2.4 基于PSO-VMD的参数寻优算法

PSO-VMD算法引入包络熵作为粒子群算法的适应度函数，VMD分解计算适应度函数值，通过对粒子速度与位置的更新，找到全局最佳的粒子速度与位置，确定VMD分解的分解层数和惩罚因子两个参数。PSO-VMD算法确定两个参数的搜索过程如下：

1)初始化PSO的参数并将包络熵Ei的最小值作为粒子群算法的适应度函数；

2)随机产生粒子种群中的粒子位置(k,α)和粒子速度vid；

3)VMD分解计算信号在不同粒子位置(k,α)下每个粒子位置对应的Ei值；

4)通过不断对比Ei的大小更新个体极值和种群全局极值；

5)利用式(7)更新粒子的移动速度和位置；

6)循环步骤3～5，当迭代次数达到预设最大值结束循环并输出最佳粒子位置(k,α)。

2.3 生命探测雷达处理方法

生命探测雷达接收到回波信号，首先滤除环境噪声，再经低噪放、混频解调、滤波等信号预处理后，采用PSO-VMD算法进行信号处理，以确定最佳的VMD分解惩罚因子和分解层数参数组合。其次，将所得到的参数组合作为VMD分解的特定参数，对回波信号进行分解，得到一系列IMF分量。接着对各个IMF分量进行频谱分析，选择能够反映生命体征信号的IMF分量重构信号。最后，对重构的呼吸心跳信号进行傅里叶变换，完成对呼吸心跳等生命特征信号频率的提取，最终实现对人体呼吸心跳的监测。具体生命探测流程如图1所示：

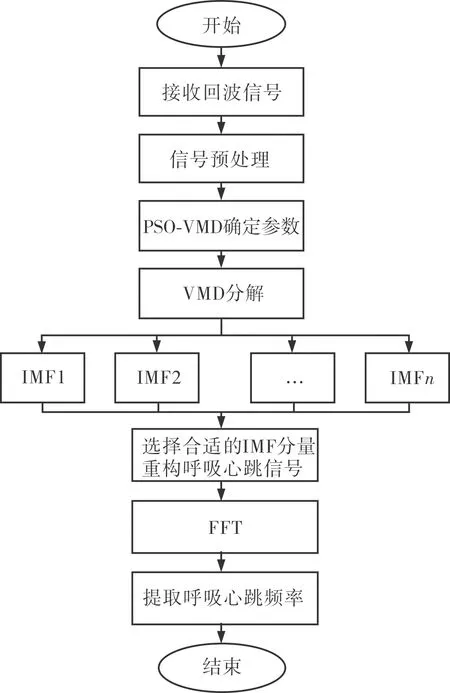
图1 生命探测雷达信号处理流程Fig.1 Block diagram of life detection radar

3 仿真实验

正常人的呼吸频率为每分钟12～44次，频率为0.2～0.8 Hz，呼吸引起的胸腔运动幅度约为1～30 mm；心跳频率每分钟60～120次，频率为1～2 Hz，心跳引起的胸腔运动幅度约为0.1～10 mm。本文假定f1=0.3 Hz，Ar=8 mm，φ1=0°；f2=1.3 Hz，Ah=2 mm，φ2=60°，雷达距离障碍物的距离为R1=3 m，距离飞行员R0=5.1 m，呼吸心跳的引起的胸腔振动模型Z(t)可表示为：

Z(t)=0.008sin(2π·0.3t)+
0.002sin(2π·1.3t+π/3)

(9)

雷达生命体征信号为：

(10)

其中，A1表示雷达穿透第一个障碍物回波信号的幅度，B表示飞行员回波幅度。

当雷达回波经过正交解调，得到同相分量I路基带信号和正交分量Q路基带信号：

(11)

其中，a是接收信号的幅度，fc为发射信号载频，Δφ(t)为总的剩余相位噪声。本文取a=1，fc=1 GHz，不考虑总的剩余相位噪声，对Q路基带信号进行分析。生命体征信号和雷达回波信号的模拟仿真图如图2所示：

图2 模拟仿真图Fig.2 Simulation diagram

将回波信号用于优化VMD参数的粒子群算法参数设置为kmim=3，kmax=10，迭代速度为1；αmin=500，αmax=3 000，迭代速度为10；初始种群规模sizepop=30，迭代次数设置maxgen=20。

用本文提出的PSO-VMD算法，取实验5组数据得到的两个最优参数如表1所列：

表1 PSO-VMD方法得到的两个参数组合

根据表1可以发现最优分解层数主要集中在8层，因此采用在分解层数8层下最接近5组惩罚因子平均数的2 374为最优的惩罚因子数。最后，选择参数组合(2 374，8)作为此类生命信号进行VMD分解的最优参数设置。生命信号采用PSO-VMD算法得到参数VMD分解下的各个IMF分量时域和频域图如图3所示：

图3 各IMF分量时域及对应的频域图Fig.3 The time and frequency domain of each IMF component

由图3可以看出，在8个IMF分量中，IMF1包含了比较丰富的低频的生命体征信息，因此，将IMF1作为重构的生命信号，并对其进行频谱分析，结果如图4所示：

图4 重构信号频谱图Fig.4 Spectrum diagram of reconstructed signal

从图4中可以看出，重构的生命信号中包含了仿真假定的心跳和呼吸频率，说明采用本文所提出的PSO-VMD算法可以有效检测出微弱的生命体信号。

在相同噪声条件下，进一步仿真对比VMD算法和EMD算法性能。EMD算法重构生命体信号与PSO-VMD算法类似，不同在于PSO-VMD只需要选择低频段的固有模态分量(IMF1)即可重构信号，而EMD要根据每个固有模态分量频谱低频分量选择总能量占比大于70%来重构生命体信号[19-20]，显然要比PSO-VMD繁琐。图5给出了相同噪声环境下，VMD和EMD算法提取呼吸心跳频率的效果。可以看出，VMD算法和EMD算法都可以准确提取呼吸频率，然而EMD方法提取的心跳频率淹没在噪声谐波中，无法准确得出心跳频率特征。这是因为EMD算法因复杂噪声影响包络线的计算，导致计算不断扩大误差，出现了模态混叠的现象，而VMD算法具有较好的噪声鲁棒性，复杂噪声对其影响不明显。所以在相同的噪声条件下，PSO-VMD算法提取呼吸心跳频率比EMD算法更准确有效。

图5 两种方法的提取心跳呼吸频率对比图Fig.5 Comparison of extraction heartbeat and respiratory rate of the two methods

4 结论

本文介绍了一种基于PSO-VMD参数优化的生命探测方法。首先，采用包络熵作为PSO算法的适应度函数，有效提取雷达接收机回波中呼吸心跳频率的生命体征信号。其次，采用PSO算法调整参数重构信号，寻找VMD最优的分解层数k和惩罚因子α，以避免因k和α不准确带来的模态模糊等问题。最后将本文所提出的算法与EMD算法进行了仿真对比，结果显示，PSO-VMD算法重构信号提取呼吸心跳频率更加准确、快速和高效。今后将进一步深入研究效果更佳的优化算法，同时结合压缩感知、稀疏重构等先进算法进一步提高探测性能。