基于HYDRUS-1D生物滞留设施雨水径流水文调控模拟
2022-05-31王浩远赵玉华李思敏
张 炜,王浩远,赵玉华,李思敏
(1.河北工程大学能源与环境工程学院,河北 邯郸 056038;2. 河北省水污染控制与水生态修复技术创新中心,河北 邯郸 056038)
近年来,为应对城市内涝频繁和水环境恶化,我国开始实施并全面推进海绵城市建设,生物滞留设施作为主要的单项海绵措施之一受到了业内广泛关注,相关理论与技术的研究不断发展[1-3]。目前,关于生物滞留设施的研究大多集中于试验或实测研究[4-5],容易受到试验装置或现场条件的制约,鉴于模型模拟可以大范围多角度地分析解决问题,且具有较好的准确性和便捷性,众多学者引入模型技术用于生物滞留设施的研发工作[6]。唐双成等[7]利用西安市1951—2007年长序列降雨过程,通过DRAINMOD模拟雨水花园长期运行效果;Gao等[8]利用RECARGA模拟生物滞留设施对降雨径流调控效应;Meng等[9]基于实测数据验证了HYDRUS-1D模拟生物滞留设施运行效果的可靠性。HYDRUS-1D是由美国盐土实验室开发的土壤环境模拟软件,可以模拟变饱和多孔介质中的一维水流入渗过程,适应范围较广,模拟结果可靠[10-11]。殷瑞雪等[12]以北京城区为背景,运用HYDRUS-1D模拟分析两种填料层生物滞留设施在不同重现期下24 h降雨过程的产流规律;李家科等[13]通过设定多组情景,利用HYDRUS-1D模拟不同填料层厚度生物滞留设施径流总量调控效果。然而,不同地区降雨特征差异较大,需根据降雨条件调整生物滞留设施结构,同时设施结构设计较为复杂,缺乏系统性研究。因此,本文通过物模试验结果率定模型参数,验证基于HYDRUS-1D生物滞留设施模型模拟结果的可靠性;通过改变降雨特征和设施结构参数,分析不同水力负荷、蓄水层高度和初始含水率条件下生物滞留设施雨水径流水文调控效应,以期为生物滞留设施的优化设计和建设提供依据和参考。
1 材料与方法
1.1 试验装置
生物滞留设施试验装置采用直径150 mm UPVC管试制,依据《海绵城市建设技术指南》中生物滞留设施的设计要求,设施自上而下分为50 mm超高层、100 mm蓄水层、150 mm种植土层、600 mm填料层和100 mm承托层,如图1所示。种植土层选用我国华北地区典型表层20 cm处粉质壤土,种植北方地区常见的早熟禾和鸢尾;填料层选用体积比1∶2的种植土加工程砂混合填料。

图1 生物滞留设施装置示意图
1.2 模型原理
HYDRUS-1D采用Richards方程来描述一维垂向水分运移过程,忽略水流水平和侧向运动[14],表达式为
(1)
K(h,x)=Ks(x)Kr(h,x)
(2)
式中:h为压力水头,cm;θ为体积含水率,cm3/cm3;t为时间,s;x为垂向坐标,cm;K(h,x)为非饱和渗透系数函数;S为源汇项,通常代表根系吸水率;β为水流方向与垂直方向夹角,取β=0;Kr为相对导水率,cm/d;Ks为饱和导水率,cm/d。
HYDRUS-1D提供了5种可选的土壤水力模型,本文选用应用较为成熟、适用范围更广的van Genuchten-Mualem模型,且忽略水流滞后现象[15],该模型方程为
(3)
(4)
(5)
其中
m=1-1/n
式中:θr为残余含水率,cm3/cm3;θs为饱和含水率,cm3/cm3;Se为有效饱和度;α为进气值倒数,cm-1;n为孔径分布参数。
1.3 试验方法
取种植土和工程砂试样风干、研磨后过2mm筛,采用筛分法与比重计法测定试验所用种植土与混合填料颗粒组成,按照美国制土壤质地三角图确定其土壤质地[16-17],采用环刀法测定容重,烘干法测定含水率,通过HYDRUS-1D自带的Rosetta软件,依据种植土与混合填料的机械组成及容重拟合水分特征曲线,预测水力模型参数[18]。为率定模型参数,验证模型的可靠性,依据邯郸市暴雨强度公式和设计径流量公式,综合实际降雨特征和生物滞留设施分布特征,选择降雨重现期为0.5 a、2 a和5 a,降雨时长为60 min、90 min和120 min的降雨过程,并且采用生物滞留设施汇流比为10∶1、15∶1和20∶1,结合正交试验原理设计9组试验,如图2所示。受试验条件的制约,试验时采用恒定进水水力负荷,同时观测和记录设施的溢流和出水过程,直至进水结束。分析生物滞留设施雨水径流水文调控影响因素时,为尽可能地模拟实际降雨过程,按芝加哥雨型确定生物滞留设施进水量,雨峰系数取0.4[19]。
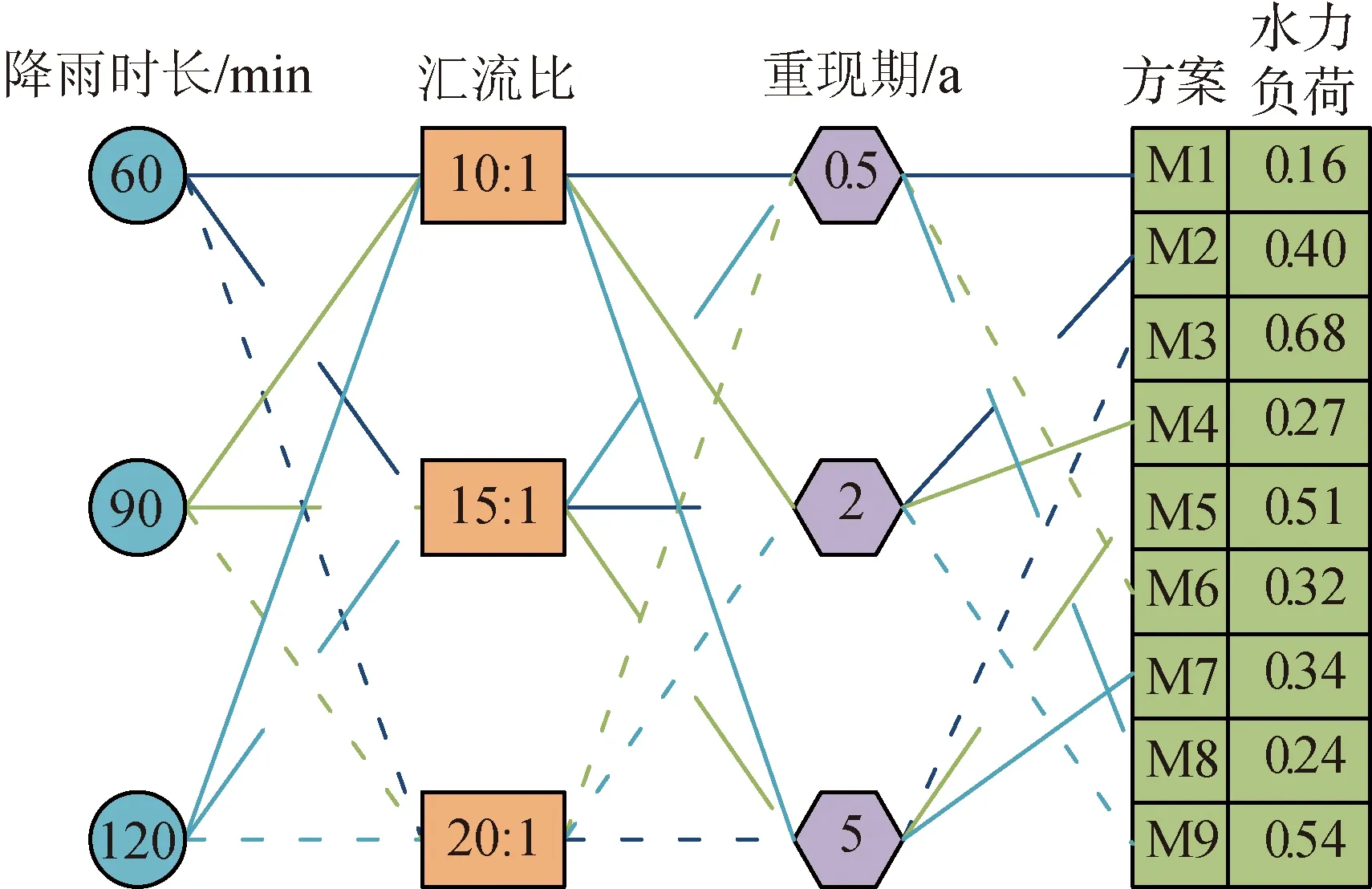
图2 试验设计
试验通过蠕动泵(保定兰格WT600-2J-A)控制装置进水流量,在装置溢流口和出水口利用容积法测定溢流量和出水量。每次试验间隔3 d,试验前测定装置种植土层和填料层初始含水率,以保证每次试验生物滞留设施各层含水率基本相同。通过HYDRUS-1D建立生物滞留设施模型,以含水率作为模型初始条件,模型上边界为大气边界条件,下边界(出水口)为自由出流边界条件,根据试验降雨时长确定模型的时间信息和输出信息,迭代信息参照模型默认值。因试验降雨时长较短,故忽略植物吸收、土壤蒸发及环境温度等对雨水径流的影响。选取M1、M4、M7方案试验数据率定模型参数,主要调整种植土层和填料层的Ks、θs及n,辅助微调θr和α[13],对比生物滞留设施溢流量的模拟值和实测值;利用M2、M3、M5、M6、M8、M9方案试验数据验证模型可靠性。在参数率定和验证模型可靠性的过程中,通过均方根误差(RMSE)、相对误差(RE)、纳什效率系数(NSE)及决定系数(R2) 4个指标判断模拟值和实测值之间的吻合度[20-21]。生物滞留设施雨水径流水文调控效应受水力负荷、蓄水层高度和初始含水率等因素的影响。采用验证后的生物滞留设施模型,通过改变不同影响因素,设定多组模拟情景,分析生物滞留设施水文调控效能,判断设施达到最佳调控效果的条件,从而达到优化和推广生物滞留设施的目的。
2 试验结果与分析
2.1 模型参数率定和验证
依据试验实测数据与模型模拟结果的吻合程度,不断优化调整种植土层和填料层对应的θr、θs、α、n、Ks等模型水力特征参数,参数率定结果见表1。将参数率定结果代入模型,利用剩余6组试验验证模型可靠性,率定期与验证期模型模拟评价结果见表2。由表2可见,模型RMSE为0.038~0.134,RE为-2.28%~7.59%,NSE为0.849~0.999,R2为0.894~0.999,表明模拟结果与实测结果基本一致,模型模拟结果可靠。

表1 模型参数率定结果
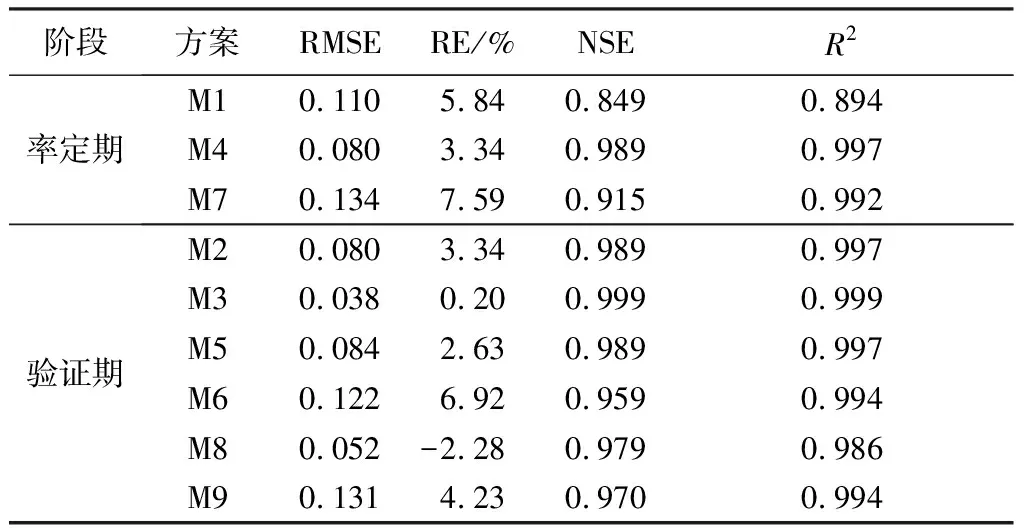
表2 模型评价结果
2.2 雨水径流水文调控效能
运用验证后的HYDRUS-1D模型,模拟生物滞留设施雨水径流水文调控效能。选取产流延迟时间t1、峰现延迟时间t2、径流总量削减率E1和径流峰值削减率E2作为生物滞留设施雨水径流水文调控效能的评判指标。仅以重现期0.5 a和降雨时长60 min作为降雨条件,以汇流比10∶1、蓄水层高度10 cm和初始含水率20%的生物滞留设施为例,其设施径流水文调控过程如图3所示。由图3可见,在雨水进入生物滞留设施初期,雨水流量较小,设施蓄水层可以蓄存一部分雨水,同时通过基质的入渗未产生溢流;当蓄水达到一定高度后,通过溢流口排出,溢流出水时间即为t1;随后溢流流量快速增加,达到峰值后呈缓慢减小趋势,进水流量峰值时间与溢流量峰值时间差值即为t2;累积进水体积随着雨水径流的变化缓慢增加,在进水流量到达峰值时快速上升,然后随着进水流量的减小缓慢增大,溢流出水伊始累积溢流体积上升速度较快,而后逐渐趋于缓慢,累积进水与溢流体积差值表示径流总量削减量,其与累积进水体积的比值为E1;进水峰值流量与溢流峰值流量的差值为径流峰值削减量,其与进水峰值流量的比值为E2。

图3 生物滞留设施水文调控过程
2.3 影响因素
2.3.1水力负荷
降雨重现期P、降雨时长Td及汇流比i是影响进水负荷的重要因素,通过模拟芝加哥雨型,根据3种影响因素设置10种模拟情景进行单因素对比试验,对比分析不同条件下生物滞留设施水文调控过程,结果如表3所示。
a.降雨重现期。根据表3对比情景1、情景2、情景3及情景4可知,在Td、i一致的情况下,分析生物滞留设施水文调控效果,随着P不断增加,t1、t2、E1和E2均逐渐减小。与P为0.5 a相比,生物滞留设施在P为5 a条件下,t1和t2分别减少9 min和2 min、E1和E2分别降低28.48%和34.22%。这是由于随着重现期的增加,生物滞留设施瞬时进水量大于等于填料渗透量的临界点前移,其产流时间和峰现时间随之提前,进水不能及时下渗的降雨时段延长,溢流量也逐渐增大。Meng等[9]在对生物滞留设施的产流模拟中,设置了不同重现期下24 h降水量,径流削减率从90.7%下降至25.8%,可见随着重现期的增加生物滞留设施对于雨水径流总量削减率不断下降。P≤1 a时,生物滞留设施的雨水径流峰值削减作用较为明显;P>1 a时,E2则由12.72%迅速下降至2.60%后又缓慢下降至2.00%,表明生物滞留设施对P>1 a的降雨径流峰值削减能力较差,且重现期越大,生物滞留设施对雨水径流峰值调控效果差异越小。

表3 不同情景水文调控模拟结果
b.降雨时长。对比情景1、情景5、情景6及情景7可知,Td取30~180 min之间时,生物滞留设施雨水径流的t1、t2分别为15~65 min、0~5 min,E1、E2分别为37.94%~70.24%、2.72%~57.37%。随着Td的增加,生物滞留设施对雨水径流调控效果的影响逐渐减小,当Td>120 min时其影响可忽略不计。这是由于随着Td增加,进水总量不断增大,而生物滞留设施填料层存在一个饱和含水率状态,一旦填料层达到饱和含水率,生物滞留设施进水将处于稳定入渗状态,其渗透能力不再随Td的延长而改变,进水量越大,其溢流量也相应增加。
c.汇流比。i是指生物滞留设施表面积与整个汇水面积的比值,是生物滞留设施主要设计参数之一。对比情景1、情景8、情景9及情景10可知,在i为5∶1~20∶1时,i=20∶1的生物滞留设施相较于i=5∶1的情况,其E1、E2分别降低73.89%、97.90%,t1、t2分别减少42 min、35 min,E1、E2、t1、t2随着i的增加先快速下降;当i>10∶1后,其下降趋势趋于平缓。由于进水量的变化并不会影响土壤填料的下渗速率,整体上随着i的增加,进水流量不断增大,设施对于径流的调控能力呈下降趋势。
2.3.2蓄水层高度
初始含水率m0=20%的生物滞留设施在P=0.5 a、Td=60 min、i=10∶1情况下,对不同蓄水层高度H的生物滞留设施进行产流模拟分析,选取H分别为0 cm、10 cm、15 cm、20 cm、25 cm,不同蓄水层高度生物滞留设施水文调控效应如图4所示。由图4可见,当进水流量一致时,随着H的增大,溢流量大大减少,并有溢流延迟现象发生。当H由0 cm变化至25 cm时,生物滞留设施的E1、E2分别为13.84%~100%、3.26%~100%,t1、t2分别为2.25~60 min、0~36 min。H为25 cm的生物滞留设施相较于H为0 cm的设施,E1、E2分别提升了86.16%、96.74%,t1、t2分别提升了57.8 min、36.0 min。并随着H的不断增加,E1、E2、t1、t2呈快速增长趋势。蓄水层高度越高,设施对于径流的调控效益越显著,与涂安国等[22]的研究结果类似。这是由于雨水径流进入生物滞留设施以后,一部分通过填料层下渗,另一部分蓄存在设施蓄水层内,当蓄存雨水超过蓄水层高度后,以溢流形式排出形成雨水径流。蓄水层高度越高,设施能够蓄积的雨水径流越多,对于雨水径流的调蓄能力越大。此外,虽然增大蓄水层高度可以显著地提高雨水径流调控能力,但也会使得积水时间大大延长,影响设施中植物的生长且导致蚊蝇滋生破坏环境,因此,设计生物滞留设施蓄水层高度时,需综合考虑多方面因素限制以使效益最大化。

(a)削减率

(b)延迟时间
2.3.3初始含水率
m0与前期干旱天数相关,前期干旱天数增加导致土壤水分通过蒸发不断减少。分别对H=10 cm的生物滞留设施在P=0.5 a、Td=60 min、i=10∶1情况下,不同m0的生物滞留设施进行产流模拟分析,选取m0分别为15%、20%、25%、30%,生物滞留设施水文调控效应如图5所示。由图5可见,当m0由15%变化至30%时,生物滞留设施E1、E2分别为49.32%~54.11%、22.84%~45.37%,t1、t2分别为24.1~25.0 min、1.0~2.5 min。随着生物滞留设施m0的不断增加,E1变化不大,而E2变化较为明显,当m0>25%后峰值削减率出现拐点,整体呈先快后慢的下降趋势;t1、t2,整体变化趋势不大。相同降雨条件下,m0越低,生物滞留设施对于雨水径流的调控效应越好,与郭瀛莉等[23]通过分析土壤前期含水率对下凹式绿地径流调控效应的影响得到的结论基本一致。这是因为土壤前期含水量较低时,土壤颗粒间的结合力很小,贮存雨水径流的有效孔隙体积变大,提高了土壤的入渗能力,导致稳定入渗阶段所需的时间也较长,从而减少地表径流,达到调控径流的作用。

(a)削减率
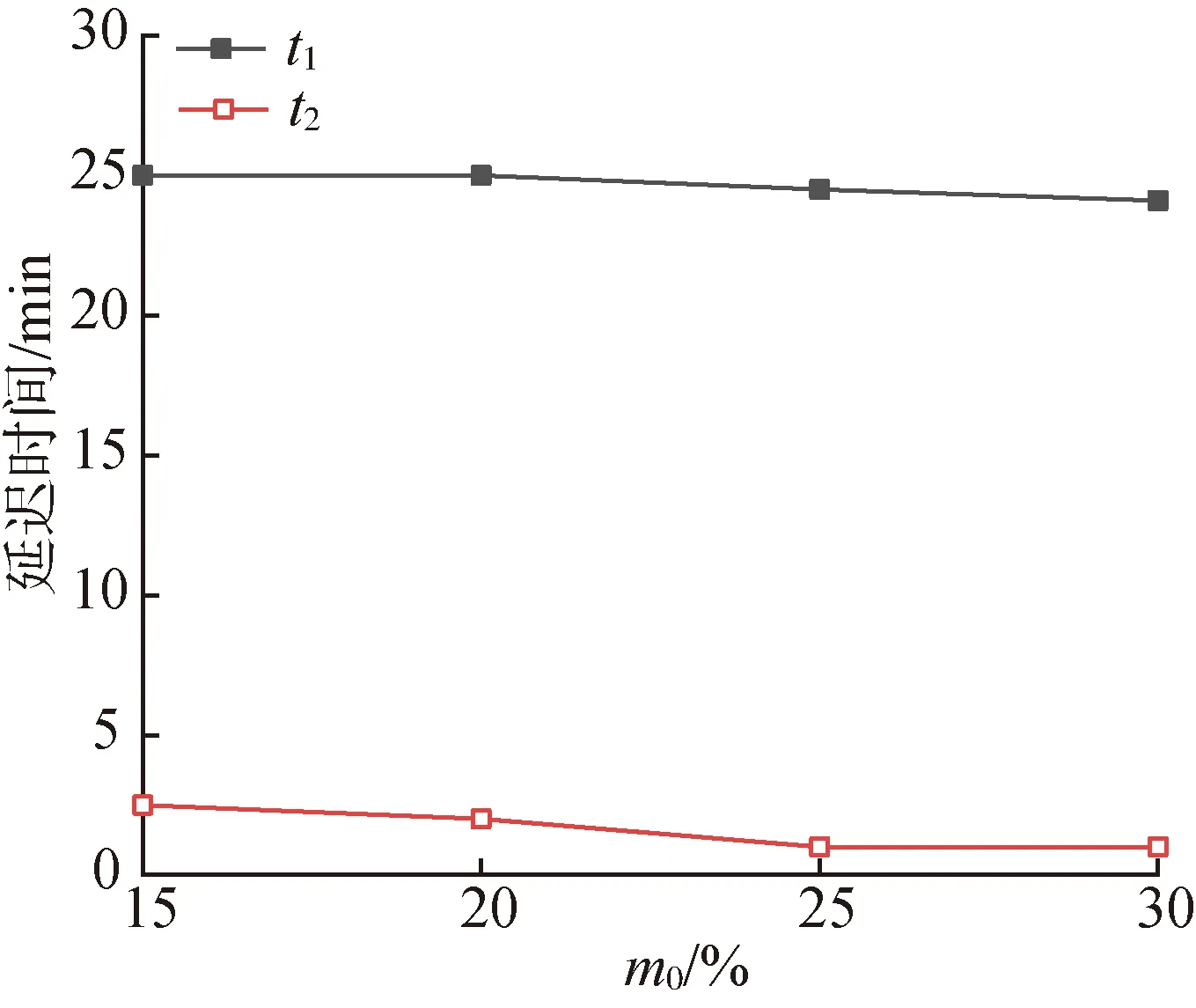
(b)延迟时间
3 结 论
a.利用实测生物滞留设施物模试验数据率定HYDRUS-1D模型参数,RMSE为0.038~0.134,RE为-2.28%~7.59%,NSE为0.849~0.999,R2为0.894~0.999,验证了模型的可靠性,可以用于分析生物滞留设施雨水径流水文效应。
b.水力负荷的变化对生物滞留设施水文调控起着重要的作用,降雨重现期从0.5 a变至5 a,径流总量和峰值削减率及产流和峰现延迟时间分别降低28.48%、34.22%、9 min、2 min;降雨时长从30 min变至180 min,径流总量和峰值削减率分别降低32.30%和54.65%,产流延迟时间增加50 min,峰现延迟时间减少5min;随着汇流比的增加,设施径流总量和峰值削减率及产流和峰现延迟时间先快速下降,当汇流比大于10∶1后,其下降趋势趋于平缓,整体上分别降低73.89%、97.90%、42 min、35 min。
c.蓄水层高度的增加显著提升了生物滞留设施水文调控效能,蓄水层高由0 cm增加到25 cm时,径流总量和峰值削减率及产流和峰现延迟时间分别提升了86.16%、96.74%、57.8 min、36.0 min,并且呈快速增长趋势;初始含水率从15%增加到30%时,其径流总量和峰值削减率分别降低4.79%和22.53%,当初始含水率大于25%后峰值削减率出现拐点,整体下降趋势先快后慢,产流和峰现延迟时间分别降低0.9 min和1.5 min,整体变化趋势不大。
