黄河源区气象干旱与水文干旱关联性分析

石 朋，詹慧婕，瞿思敏，冯 进，管晓祥

(河海大学水文水资源学院，江苏 南京 210098)

全球气候变暖背景下的干旱问题日益突出，干旱导致的水资源短缺进一步加剧了人类的用水紧张程度[1]，同时导致土地退化以及极端天气和复合型灾害的发生[2-3]。1972—1997年黄河经历了漫长的干涸时期，并在20世纪90年代初出现干旱历时延长、干旱频率增加的现象[4]。1997年在中国北方发生的严重干旱导致黄河出现为期226 d的零径流，造成了严重的社会经济损失[5]。准确表征黄河流域干旱特征及变化规律，对确保黄河流域生态保护与高质量发展具有极为重要的意义。

干旱分为4种类型，气象干旱、水文干旱、农业干旱和社会经济干旱[4]。降水的亏缺会导致气象干旱，地表水及地下水的亏缺会引发水文干旱，这两类干旱对人类社会产生了广泛的影响。一般使用干旱指数来表征气象和水文干旱，标准化降水指数(standardized precipitation index，SPI)只需要降水序列作为输入，并且能将降水分布转化为正态分布，从而克服非标准化分布带来的差异，因此被广泛应用于气象干旱分析[6]。同样，标准化径流指数(standardized runoff index，SRI)只需流量序列，且计算简便，因而被应用于水文干旱分析[7]。

一般情况下首先发生气象干旱，气象干旱会向水文干旱和农业干旱传播[8]，因而越来越多的学者研究气象干旱与水文干旱之间的联系。准确描述气象干旱和水文干旱的关系可以在气象干旱的初期及时向决策管理者预警，减轻水文干旱带来的社会经济损失。Li等[9]采用小波分析法发现，沙颍河上游气象干旱和水文干旱之间的传播时间随季节变化明显；Dehghani等[10]基于阿基米德Copula气象干旱指数对水文干旱进行概率性预报；Yu等[11]研究了淮河上游嵌套流域的气象干旱到水文干旱的传播时间，发现流域越大，气象干旱引发的水文干旱持续时间越长。但是，由于不同流域降水条件及调蓄能力的不同，气象干旱到水文干旱的传播存在较大差异，目前对黄河源区开展的研究局限于气象及水文干旱特征、干旱的时空变化规律等[12-13]，黄河源区气象干旱与水文干旱的关联性及干旱传播时间尚未探明。

刘永佳等[14]利用皮尔逊相关分析方法分析了黄土高原气象干旱到水文干旱的季节性传播规律；杨铭珂等[15]利用皮尔逊相关分析方法，发现黔中地区不同季节气象和水文干旱的最佳时间尺度和滞后时间不同；Wang等[16]利用交叉小波及小波相干方法探究了黄河流域气象干旱到水文干旱的传播特征。目前研究干旱的传播规律多使用皮尔逊相关分析方法，结合1～2种小波方法进行干旱周期变化规律的研究，而利用多种小波方法探明区域化干旱传播特征及气象干旱与水文干旱的内在联系性的研究相对较少。

黄河源区是重要的水资源保护地，本研究聚焦黄河源区区域化气象干旱与水文干旱的关联性及水文干旱的滞后效应，侧重对黄河源区区域化规律进行研究，利用最优的SPI-n(n为月时间尺度，n=1,2,…,24)和SRI拟合结果，探究黄河源区气象干旱向水文干旱的最佳传播时间，基于连续小波变换、交叉小波变换和小波相干来分析黄河源区气象干旱和水文干旱的周期性变化规律及其关联性，以期为流域干旱灾害预警及防治提供参考。

1 研究区概况与研究数据

黄河源区位于青藏高原东北部(95°50′E～103°30′E，32°30′N～36°00′N)，流域面积约12.19万 km2，主要控制水文站为唐乃亥水文站。黄河源区地势起伏较大，从西到东地势逐渐下降，平均高程约为4 425 m，多年平均降水约510 mm[17]，汛期集中在夏季，多年平均径流量约占黄河流域的38%。黄河源区下垫面类型主要以高寒草甸、季节性冻土和多年冻土区为主[18]，流域的水文站、气象站及水系分布如图1所示。

图1 黄河源区水系分布

本文采用的90 m分辨率SRTM DEM原始高程数据来自地理空间数据云(http://www.gscloud.cn/)。黄河源区内部7个气象站(玛多、兴海、达日、河南、玛曲、若尔盖、红原)1967—2020年的日降水数据来自中国气象数据网(htttp://data.cma.cn/)，经过日累加处理得到月降水数据。唐乃亥水文站1967—2020年的月流量资料来源于水文年鉴，数据经过严格质量控制和检查。

2 研究方法

2.1 Kolmogorov-Smirnov检验

Kolmogorov-Smirnov(KS)检验是一种拟合优度检验方法。根据一个给定的概率分布，利用经验累积分布函数(empirical cumulative distribution function，ECDF)和累积分布函数(cumulative distribution function，CDF)之间的差异计算拟合优度。KS检验包含一个统计量D，若D值大于某一临界值，则拒绝假设的概率分布[19-20]。

2.2 气象干旱与水文干旱指标

SPI是一种常见的气象干旱指标[21]，一般选用Gamma分布来拟合降水时间序列[22]。SRI被用来刻画水文干旱[7]，计算SRI的步骤和计算SPI的类似，需要将降水时间序列替换成流量时间序列，并且分布函数因区域而异，流量序列可能适用于Gamma分布、皮尔逊Ⅲ型(P-Ⅲ型)分布、广义极值(GEV)分布、对数正态(Log-Normal)分布等。

2.3 皮尔逊相关系数

皮尔逊相关系数可以表示两个变量之间的相关关系[23]，相关系数越大，表示两个变量线性相关越强，范围在[-1,1]之间。

2.4 面平均降水量计算方法

由于降水空间分布不均匀，不同的面平均降水量计算方法可能会影响计算结果，本文挑选3种常用的降水空间插值方法来计算面平均降水量，分别为算术平均法、泰森多边形法和距离平方倒数法[24]。

2.5 小波分析方法

连续小波变换可以用来分析时间序列中的局部间歇性振荡，同时可以分析出时间序列的周期性变化规律[25]；交叉小波变换和小波相干可以用来检验两个时间序列之间的相关关系，其中，交叉小波变换用来检测两个序列高能量区域的相关性[16]，小波相干则用来检测两个序列间低能量区域的相关性[26]。

3 结果与分析

3.1 最优流量分布筛选

由于气候变化、人类活动等因素，流量的概率分布存在区域性差异[16]，需要依据实测数据筛选出最适宜的流量分布函数。本研究选择6种常见的分布函数[19]来拟合唐乃亥站1967—2020年的月流量，包括GEV分布、威布尔(Weibull)分布、广义帕累托(广义Pareto)分布、Log-Normal分布、对数Logistic(Log-Logistic)分布、P-Ⅲ型分布。

利用KS检验来验证6种分布函数与经验分布的逐月差异，差异程度由假设检验结果的判定参数p值来表征。p越接近1，表示分布越接近真实情况，在p<0.05的阈值下[9,23]，除了广义Pareto分布被拒绝，其他5个分布均通过KS检验，如图2所示，其中红空心点代表异常值，黑实心点代表均值，箱内黑线代表中位数。

分析发现，GEV分布p最小值(0.321)和平均值(0.796)都高于其他分布；Weibull分布虽然也通过了KS检验，但在唐乃亥水文站的应用上并不理想；Log-Normal和Log-Logistic分布拟合结果较为接近，P-Ⅲ型分布拟合结果略次于Log-Normal和Log-Logistic分布。

根据p值选择每个月最优的流量CDF如图3所示，GEV分布在6个月份中表现出最优的性能，综合考虑选择GEV分布作为最优流量CDF进行后续计算。

图2 5种分布经过KS检验后的p值

3.2 SPI和SRI的计算

由于降水具有空间不均匀性[27]，为了使计算更切合实际，减少降水输入的不确定性，利用算术平均法、泰森多边形法和距离平方倒数法分别处理1967—2020年的月降水量，得到流域月尺度面降水量。

根据3种降水插值方法得到的月尺度流域面降水量，使用Gamma分布计算气象干旱指数SPI-n(n=1,2,…,24)。以往的研究结果表明[14]，1月尺度的SRI指数最具有代表性，所以最优流量分布利用GEV分布函数，计算水文干旱指数SRI-1。利用皮尔逊相关系数，分析由3种降水插值方法计算的SPI-n与SRI-1之间的相关关系。结果表明，3种方法得出的SPI-9与SRI-1拟合效果最优，皮尔逊相关系数分别为0.68、0.67、0.68，3种方法计算结果较接近，黄河源区气象干旱向水文干旱的传播时间为9月。基于以上结果，本次研究选择距离平方倒数法进行后续研究。

基于距离平方倒数法计算的SPI-9和基于GEV分布函数计算的SRI-1如图4所示。由于SPI-9采用了累计9月的降水进行计算，为了保证流量序列和降水序列的一致性，降水和流量序列统一取1968—2020年。根据SPI和SRI的值划分干湿等级[14]，结果表明，SPI-9和SRI-1表征的干湿程度基本一致，气象干旱与水文干旱发生年份几乎重叠。黄河源区在1969—1971年和1973年发生了严重气象干旱和中度水文干旱事件，在1977—1978年发生了严重气象干旱和水文干旱事件，在1985—2005年间歇性地发生了气象和水文干旱事件，每次发生干旱的持续时间较长，在2003年发生了极端气象和水文干旱事件，在2005—2020年发生干旱的严重程度减小，干旱发生频率也较1985—2005年减少。周帅等[5]指出2005年以后由于降水减少幅度缓解的原因，黄河流域干旱严重程度减小，这与本文的研究结论一致。

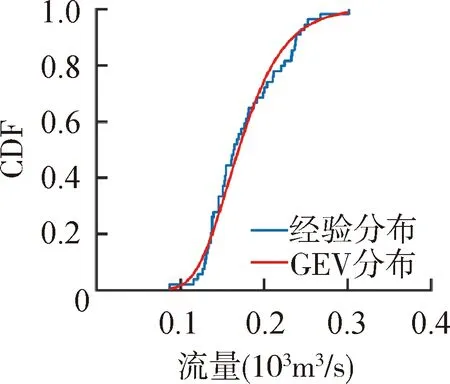
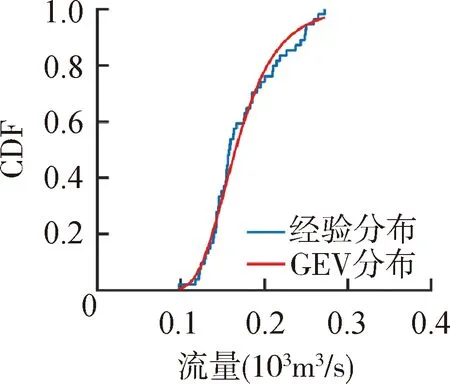
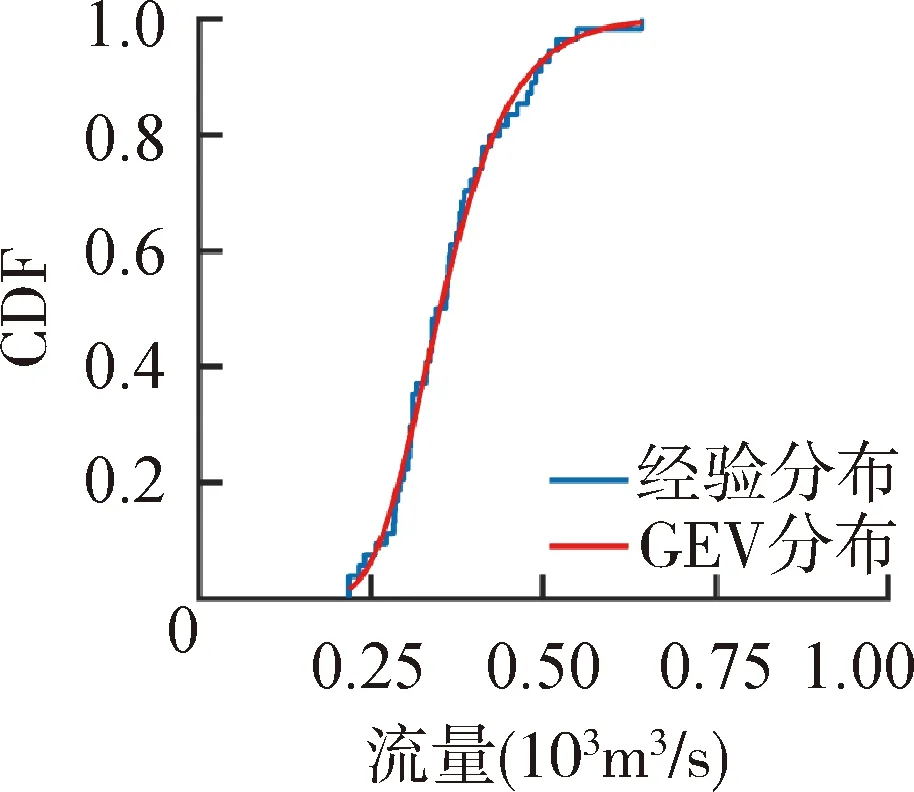
(a)1月 (b)2月 (c)3月 (d)4月

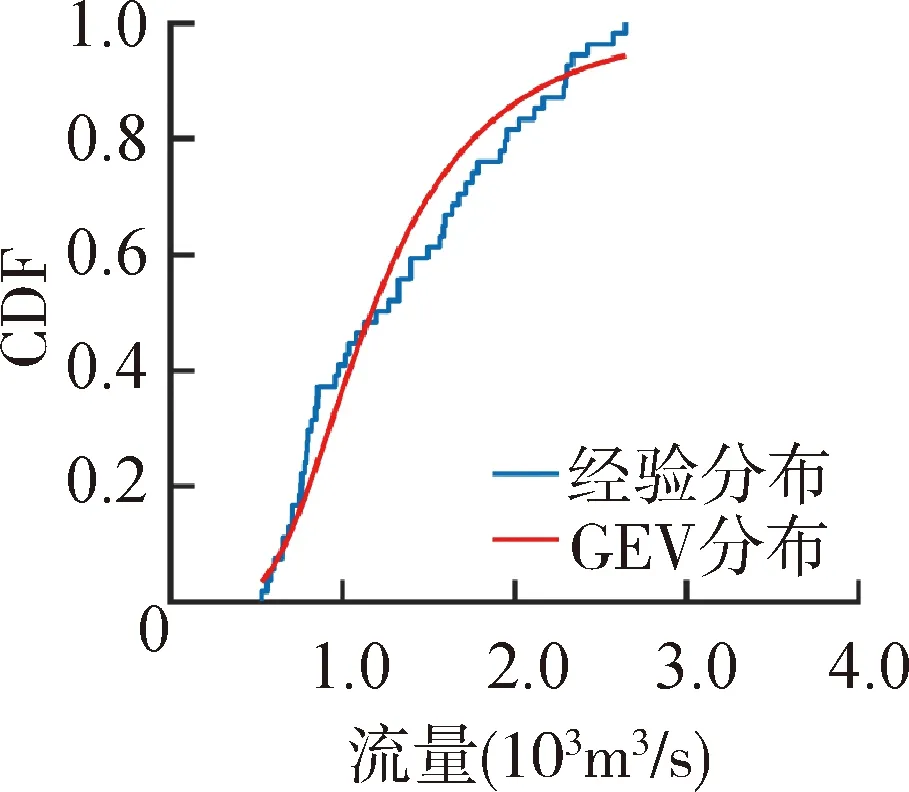
(e)5月 (f)6月 (g)7月 (h)8月

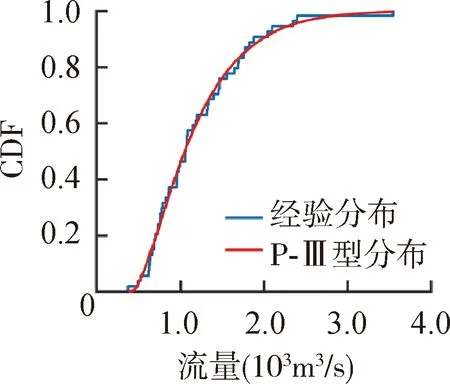
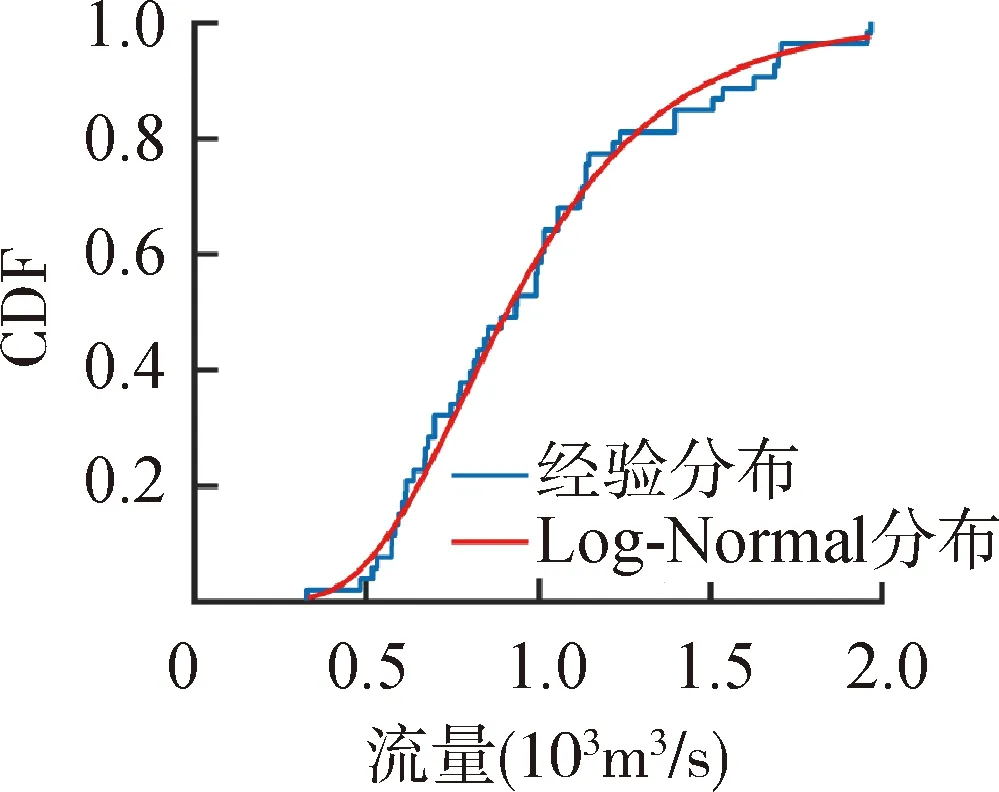
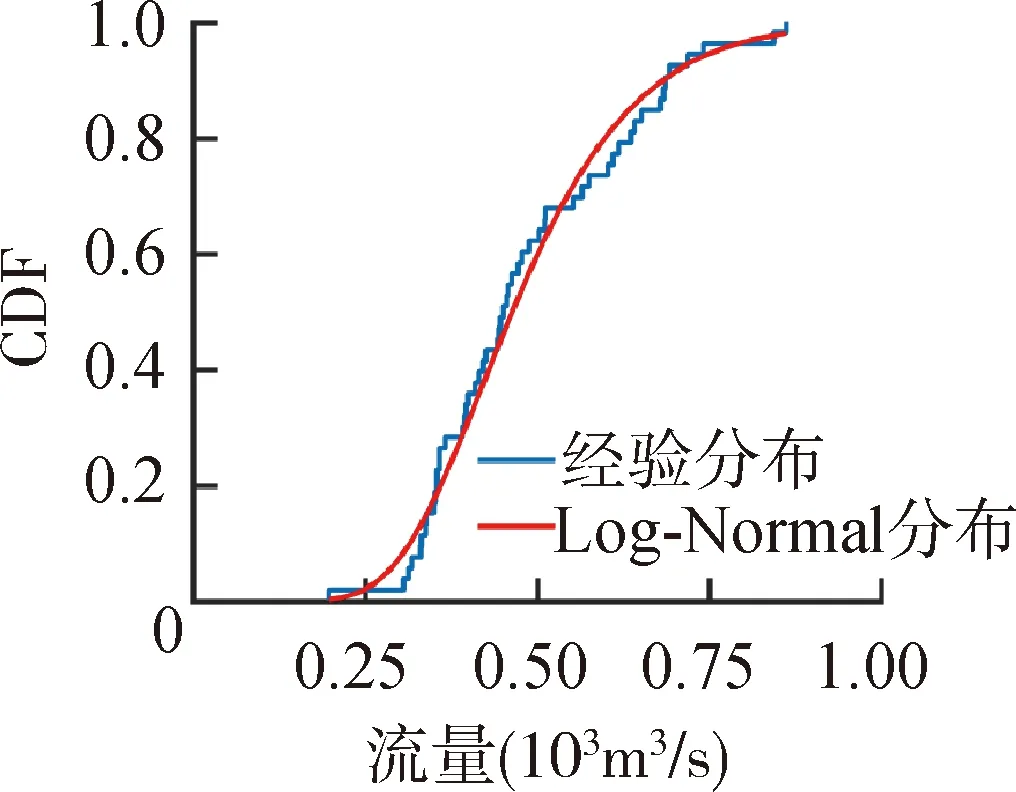
(i)9月 (j)10月 (k)11月 (l)12月

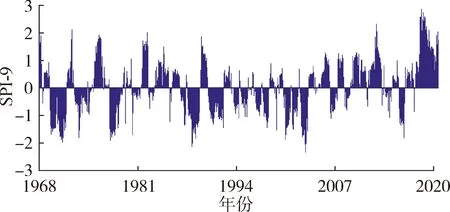
(a)SPI-9

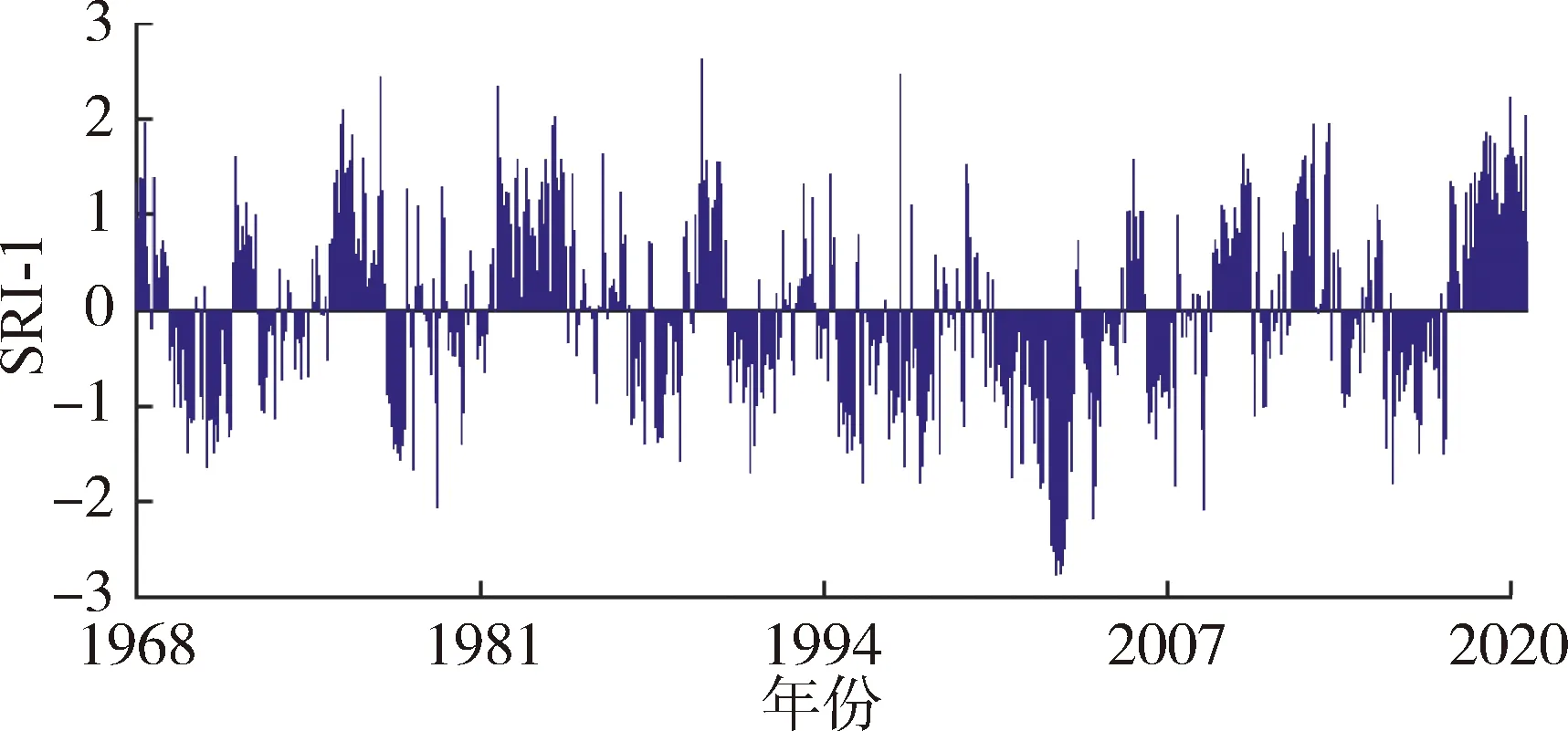
(b)SRI-1

3.3 气象干旱和水文干旱关联性

先用连续小波变换分析气象干旱和水文干旱的周期性变化规律，再用交叉小波变换分析高能量区域的气象干旱和水文干旱的联系，对于低能量区域，则选择小波相干法分析两者的联系。

图5给出了1968—2020年SPI-9和SRI-1的连续小波功率谱，图中影响锥表示不受小波光谱边缘效应影响的彩色区域，粗轮廓线表示相对于红色噪声的95%置信水平。结果表明，对于SPI-9序列，在95%的置信水平下，1972年5月至1978年2月、1988年3月至1992年2月、1997年12月至2002年10月、2002年10月至2008年12月的小波高功率分别在37～50月、29～42月、12～16月、18～26月之间，持续时间约为4～6 a。1971年9月至1973年4月、1988年7月至1990年2月、2015年5月至2017年9月的小波高功率都在17～22月之间，持续时间较短，约为2 a。对于SRI-1序列，在1978—2016年间，2～8月周期的小波功率值较大，持续时间较短，表现为准周期的间歇性振荡。SRI-1最明显的周期是78～105月，持续时间是1977年6月至1986年7月。SRI-1在1988年9月至1992年2月的小波高功率在37～47月之间，与SPI-9在相同时间段的周期性较接近。

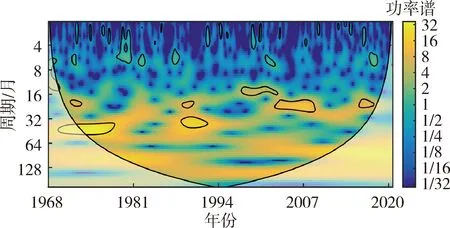
(a)SPI-9

(b)SRI-1

在37～42月的周期，SPI-9和SRI-1序列都在1988年9月至1992年2月有较高的功率值，说明黄河源区的气象干旱和水文干旱具有相似的周期特征。

图6(a)为SPI-9和SRI-1的交叉小波功率谱图，向右箭头表示SPI-9和SRI-1序列相位变化相同，向左箭头表示两序列相位变化相反。SPI-9和SRI-1序列在1973年4月至1979年4月和在1978年9月至1984年8月分别呈现出37～53月和83～105月的显著正相关，在1987年8月至1994年3月间呈现出31～50月的显著正相关，在2002年3月至2009年6月间呈现出14～25月的显著正相关。SPI-9和SRI-1的小波相干图如图6(b)所示，向右的黑色箭头表明SPI-9和SRI-1序列具有相同的相位，且存在比较连续的小波显著相干，具体表现在1971—2016年。SRI-1的振荡可以较好地用SPI-9来表述，周期为16～176月不等。

连续小波分析、交叉小波分析和小波相干分析结果表明，在不同的时间段，SPI-9和SRI-1均存在明显的相关性，SPI-9序列可以用于黄河源区的水文干旱监测。

4 结 论

a.选择的6种分布中，广义Pareto分布函数被KS检验拒绝，其他5种分布均通过检验，GEV分布表现最优，然后依次是Log-Normal分布、Log-Logistic分布、P-Ⅲ型分布，Weibull分布表现最差。

(a)交叉小波

(b)小波相干

b.3种降水插值方法中，算术平均法、泰森多边形法、距离平方倒数法计算结果接近，在黄河源区适用效果均良好。由距离平方倒数法计算的SPI-9和GEV分布计算的SRI-1拟合效果最优，皮尔逊相关系数为0.68，气象干旱和水文干旱发生的年份基本一致，两者存在密切联系。

c.连续小波变换分析表明SPI-9和SRI-1具有类似的周期特征。交叉小波变换表明SPI-9和SRI-1在1973年4月至1979年4月、1978年9月至1984年8月、1987年8月至1994年3月、2002年3月至2009年6月分别呈现出37～53月、83～105月、31～50月、14～25月的显著正相关。小波相干表明SPI-9能较好地表述SPI-1的振荡性，在1971—2016年呈现出16～176月的周期。