刚性接触网跨距的速度适应性研究
2022-05-31乔锦新
乔锦新


摘 要:为研究不同速度等级下刚性接触网的标准跨距值。本研究利用弓网动态仿真手段,选取弓网接触力标准差、最大值、最小值为性能指标,比较分析刚性接触网跨距为6 m和8 m时不同运行速度、不同受电弓类型下的弓网动态性能。为得到更优的弓网接触力性能指标,刚性接触網在160 km/h及以下速度运行时,对应的标准跨距宜选用8 m;在200 km/h及以下速度运行时,对应的标准跨距值宜选用6 m;DSA250型受电弓与6 m跨距刚性接触网的接触质量具有优势,统计值能满足240 km/h运行要求。
关键词:弓网仿真;刚性接触网;跨距;接触力
中图分类号:U225.1 文献标志码:A 文章编号:1003-5168(2022)9-0084-04
DOI:10.19968/j.cnki.hnkj.1003-5168.2022.09.018
Study on the Dynamic Performance of Overhead Conductor Rail and Pantograph with Different Rail Span
QIAO Jinxin
(China Railway First Survey & Design Institute Group Co., Ltd., Xi'an 710075, China)
Abstract: In order to study the standard span value of rigid catenary under different speed grades. This paper uses the pantograph dynamic simulation method to select the standard deviation, maximum and minimum of the pantograph contact force as performance indicators, and compares and analyzes the rigid catenary spans of 6 m and 8 m at different operating speeds and different pantograph types. Dynamic performance of bow net. In order to obtain a better performance index of the pantograph and net contact force, when the rigid catenary is operating at a speed of 160 km/h and below, the corresponding standard span should be 8 m; when operating at a speed of 200 km/h and below , the corresponding standard span value should be 6 m; the contact quality of DSA250 pantograph and the rigid catenary with 6 m span has advantages, and the statistical value can meet the 240 km/h operation requirement.
Keywords:pantograph and net simulation; rigid catenary; span; contact force
0 引言
2002年,刚性接触网在广州市地铁二号线取得试挂成功。自此以后,刚性接触网作为一种架空接触网在城轨交通中得到大量应用[1]。与柔性接触网相比,由汇流排固定接触线的刚性悬挂模式具有载流量大、维修少、无断线事故等优点[2]。
对于刚性接触网的研究,其核心在于弓网关系。而迄今国内外对弓网关系的研究主要集中在如何建立弓网模型、基于已有弓网结构下的动力响应分析等方面,而研究弓网结构优化问题则较少[3]。江洪泽[4]对刚性接触网弓网受流进行了研究,在运行速度不超过80 km/h的前提下,提出了不离线受流约束模型。王世轩[5]基于模态叠加法理论建立接触网动力模型,并对刚柔过渡及锚段关节复杂位置处的弓网动力性能进行了研究。原华[6]则对锚段关节及中间接头特殊部位的弓网受流进行研究。MAK[7]则从建设成本、可靠性、可维修性等方面对刚性接触网优势进行了分析。仿真分析结果表面,刚性悬挂模式可达130 km/h的运行速度[8]。目前,国内外学者较多通过建立弓网有限元模型研究单因素下的弓网动力响应,其影响因素包括运行速度、接触力、悬挂结构及受电弓弓头质量等。而接触网跨距将直接影响刚性接触网的动态受流[9]。目前,运行速度大于160 km/h的刚性接触网标准跨距有6 m和8 m两种,但尚未对两种标准跨距的速度适应性进行深入研究。
本研究搭建弓网仿真动态模型,以接触力为性能指标,对比分析接触网跨距为6 m和8 m时,在不同运行速度、不同受电弓类型下的弓网动态性能,提出160 km/h和200 km/h运行速度下的刚性接触网标准跨距值,为刚性接触网工程设计提供指导。
1 受电弓与刚性接触网仿真建模
1.1 受电弓模型
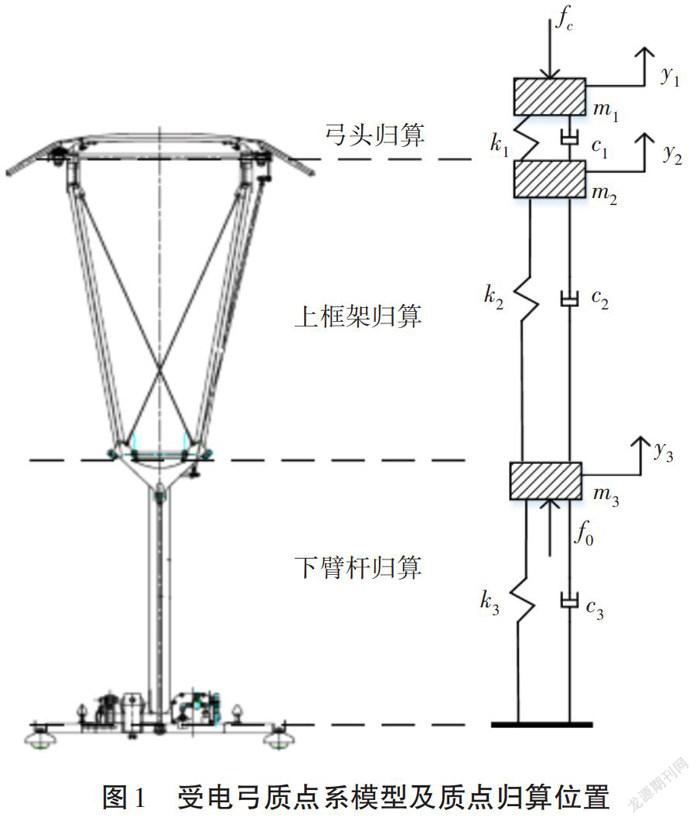
借助质点系模型对受电弓垂直方向振动行为进行分析,等效为质量-弹簧-阻尼若干单元,具体如图1所示。
可以选取三种满足最高速度为160~200 km/h的受电弓型号,其质点系模型参数见表1。
1.2 接触网模型
在建立刚性接触网空间动力学模型过程中,考虑拉出值变化、汇流排截面惯性矩大的原因,按照“S”或“C”字形考虑;拉出值相比于锚段长度而言可忽略,接触网汇流排梁单元可视为直梁,模型空间推广到三维空间,刚性接触网的空间有限元模型[10],具体如图2所示。
重疊区域单元和节点不存在约束关系,使受电弓从第1支刚性接触网过渡到第2支刚性接触网,锚段关节区段受电弓会在某个范围与两支接触网接触,该区域应增加单元数量。对两支接触网进行了离散化处理,8和9节点存在边界约束,具体如图3所示。
2 跨距对弓网动态性能的影响分析
2.1 跨距6 m
刚性接触网跨距值设为6 m,拉出值设为300 mm,基于前面搭建的刚性接触网模型,搭建锚段长度皆为250 m的刚性接触网两锚段仿真模型[11]。
刚性接触网的悬挂结构具有一定的刚度,但由于目前缺少相关资料,现假设刚性接触网的悬挂结构为刚性悬挂,定位点刚度选取6.7×107 N/m。
当接触网跨距为6 m时,以DSA200、DSA250、DSA380三种类型受电弓为例,对不同速度运行下的接触力进行仿真。得到接触力标准差、最值和0.3Fm-σ(0.3倍平均接触力减标准差)如图4、图5、图6所示。
从图中可以看出,160 km/h及以下运行速度时三种类型受电弓的接触力标准差、最值和0.3Fm-σ增幅相当;以200 km/h及以上速度运行DSA200、DSA250、DSA380型受电弓的接触力标准差、最值和0.3Fm-σ增幅出现较大差异;DSA200型受电弓在220 km/h速度等级时接触力最小值或0.3Fm-σ超出标准要求,而DSA250、DSA380型受电弓增加至240 km/h速度等级时也出现超标。
2.2 跨距8 m
当接触网跨距为8 m时,得到上述三种3种受电弓接触力标准差、最值和0.3Fm-σ如图7、图8、图9所示。从图中可以看出,160 km/h及以下运行速度时DSA200、DSA250、DSA380型受电弓的接触力标准差和0.3Fm-σ增幅相当;速度在100 km/h时的接触力标准差、最值差比60 km/h和120 km/h时大,此速度等级下与受电弓固有频率接近[12],故振幅较大;DSA200、DSA250、DSA380型受电弓在220 km/h速度等级时接触力最小值或0.3Fm-σ超出标准要求。
2.3 不同跨距接触力指标比较
综合以上分析,不同跨距下当受电弓与刚性接触网运行速度超过一定值时,接触力标准差翻倍、甚至会翻几倍,接触力波动变化剧烈,但在该值以下DSA200、DSA250、DSA380型受电弓的接触力标准差随速度增加而逐步递增,增加幅度缓和。
不同类型、不同跨距的受电弓接触力标准差如图10所示。由图可知,不同跨距对DSA200受电弓的影响较小,理论最高运行速度为200 km/h。跨距变大对DSA250、DSA380受电弓的接触力有一定影响,理论最高运行速度有所减小。由接触力标准差可知,运行速度在160 km/h及以下时,两种跨距接触力具有相近的离散程度,看不出何种跨距具有优势,但运行速度在200 km/h以上时,DSA250型受电弓与6 m跨距刚性接触网的接触质量具有优势,统计值能满足240 km/h运行要求。
为进一步比较DSA380受电弓在不同跨距的接触力最值变化情况,如图11所示。
通过对比发现,当运行速度在200 km/h及以下跨距为8 m时接触力最大值比跨距6 m小,前者的接触力最小值比后者的大,最值差小。200 km/h以上速度等级跨距6 m时最值范围具有优势。
3 结论
利用弓网动态仿真手段,针对刚性网在不同跨距(6 m、8 m)、不同速度、不同受电弓类型,得出以下结论。
①运行速度不大于160 km/h时刚性接触网宜选用跨距8 m作为标准跨距值。
②运行速度不大于200 km/h时刚性接触网宜选用跨距6 m作为标准跨距值。
③DSA250型受电弓与6 m跨距刚性接触网的接触质量具有优势,统计值能满足240 km/h运行要求。
以上研究结论可为160~200 km/h刚性接触网工程提供理论设计依据。
参考文献:
[1] 关金发,吴积钦,方岩.刚性接触网的研究综述及展望[J].都市快轨交通,2016(6):37-43,59.
[2] 裴志禹.AC25kV刚性接触网过渡段结构优化研究[D].成都:西南交通大学,2018.
[3] 关金发,田志军,吴积钦.基于弓网动力仿真的160 km/h刚柔过渡系统方案研究[J].铁道报.2018(9):48-56.
[4] 江洪泽.城市轨道交通刚性接触网弓网受流理论探析[J].都市快轨交通,2010(4): 54-58.
[5] 王世轩.城市轨道交通弓网建模方法适用性研究[D].成都:西南交通大学,2014.
[6] 原华,张庆贺,毕继红.刚性接触网特殊部位处受流质量的分析[J].低温建筑技术, 2008(2):58-60.
[7] MAK M K. Adoption of Overhead Rigid Conductor Rail System in MTR Extensions[J]. Journal of International Council on Electrical Engineering, 2012(4): 463-466.
[8] 关金发.受电弓与刚性接触网动力相互作用研究[D].成都:西南交通大学,2016.
[9] 梅桂明.受电弓-接触网系统动力学研究[D].成都:西南交通大学,2010.
[10] 高伟,李军,黎莉莉,等.160 km/h速度等级刚性接触网条件下弓网关系研究[J].电力机车与城轨车辆,2021(4):82-84,98.
[11] 孙宁,陈珍宝,梁坤,等.160 km/h速度等级刚性接触网受电弓弓网动态仿真分析[J].电力机车与城轨车辆,2020(3):49-51.
[12] 李鲲鹏,关金发.轨道交通架空刚性接触网强度匹配仿真研究[J].计算机仿真,2019(8):145-150,297.
