基于贝叶斯优化的密度峰值聚类算法

吴涛 朱小东 刘唤唤 张顺香

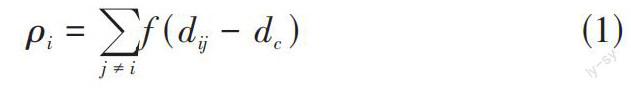
摘要：针对人工经验设定密度峰值的聚类算法（clustering by fast search and find of density peaks， DPC）的截断距离[dc]有很大的主观性和随机性，进而导致密度峰值聚类算法的性能无法完全发挥的问题。提出贝叶斯算法（Bayesian Optimization，BO） 优化密度峰值的聚类算法以实现自适应聚类。并解决密度峰值的聚类算法簇间数据点识别错误问题。该方法建立在数据集Aggregation、Flame、Jain、Spiral上进行实验，分别通过内部指标Silhouette和外部指标F-measure对实验结果评估，性能均有提升。

关键词：密度峰值的聚类算法;截断距离;贝叶斯算法;自适应聚类;内部指标

中图分类号：TP391      文献标识码：A

文章编号：1009-3044（2022）22-0008-05

1 引言

21世纪随着互联网的快速普及，人们在形形色色的生活中产生了大量的数据，大数据的时代随之来临，怎样从这些数据中获得有用的信息成为当今研究热点。

聚类是数据挖掘、机器学习、图像识别等领域预处理数据的一种基本算法。聚类把一组没有标签定义的数据集或者样本集，依据样本的一组特征值，按照某种相似性度量手段将特征值相似度较高的数据点划分成同一个类簇，为后续处理提供了可贴标签的分类数据。

聚类是一种无监督学习，即在无任何人工干预的情况下对数据进行区分。相似度高的数据聚合成一类簇。不同簇之间的样本点相似性较低[1-2]。有监督学习主要任务是分类，通过很多已经标记过的数据来对新数据进行区分。相比监督学习，无监督学习则不需要大量人工标记的训练样本来作为区分数据的前提。在大数据信息共享时代，因为数据聚集模式复杂、多变，单一相似度标准难以适应多种模式，所以现有的聚类算法不能够满足已有种类繁多的数据集。面对以上现状，不断衍生出众多的聚类方法。目前常用的聚类算法大致可分为：基于模型的聚类，基于划分的聚类，基于层次的聚类，基于网格的聚类，基于密度的聚类。其中，基于模型的聚类算法一般假设要聚类的数据来源于某个混合的潜在概率分布模型，通过对该模型进行参数估计来完成聚类。基于划分的聚类算法需要一个最优化的目标函数来发现聚类数据中的类别信息，迭代的将数据集划分为几个部分，再验证划分过程是否科学合理。常见的划分聚类算法如K-means[3]，该算法简单并且高效，聚类效果主要受类簇中心点[k]值影响较大。一般情况下[k]值的确定具有很大的主观性，这对没有先验经验的测试下的取值会对聚类结果有很大的影响。面对高维的数据处理对象聚类效果不佳。基于网格的聚类算法对数据的处理比较粗糙，主要用于处理大量多维数据的聚类问题。基于层次的聚类算法分为自下而上的聚合层次聚类和自上而下的分裂层次聚类，其目的是让聚类过程不受参数的影响并且更加灵活。基于密度的聚类核心思想是先选定较高密度的数据点，再将周边与其相近的点聚为一类。常见的基于密度的聚类算法如DBSCAN[4]聚类算法虽然能够处理任意大小形状的簇，对噪声的容忍性较好，但当簇密度变化较大时聚类效果较差，并且当遇到大量高维的数据时会大量地消耗计算资源。

DPC算法[5]是近几年提出的一种基于密度划分的聚类算法，该算法依据密度峰值决策图选取合适的密度峰点;并将图中代表样本的其他数据点划分到最近或匹配的密度峰点类别中，从而得出簇的划分。DPC算法的优点之一是除了决策图中的密度峰值点需要人工干预选择外，整个算法仅需要预先给出一个输入参数（截断距离） ，不需要像多数其他聚类算法一般预先指定簇数目，提高了算法的可靠性与适应性。另一方面，DPC算法在初期决策图中选择的密度峰点即確定了簇的数目及分布，不需要通过反复迭代来获得最优结果，其效率相对于其他聚类算法有着显著优势。

随着对DPC算法的不断深入研究，越来越多的改进DPC算法相继出现。针对DPC算法的局部密度计算方式过于单一的问题，Liu等人[6]提出ADPC结合KNN的算法，该算法重新定义了局部密度的计算方法。针对DPC算法的一次性样本数据分配策略可能存在错误分配连带问题，即一旦一个数据点被错误分配，随后可能会有更多的点被错误分配，Seyed等人[7]提出了一种DPC-DLP的聚类算法，该算法统一确定簇中心，将簇中心联合起来构建新的KNN图，通过图的传播方法分配样本数据。Xie[8]等人提出了计算数据[ai]相对于[其K]近邻的局部密度度量方式和通过从聚类中心开始对点的K个最近邻进行广度优先搜索来分配数据点，从而对DPC聚类算法进行优化。

面对不同类型数据时，这些改进的DPC聚类算法虽然有较好的聚类结果，但是截断距离仍需要人为设定。当数据密度相差较大时，很难人为选择一个合适的截断距离，如果输入截断距离百分比过大时可能会出现所有数据点都被分到同一类，如果输入截断距离百分比过小时可能会出现聚类数目过多。所以截断距离[dc]是影响聚类效果好坏的重要参数，截断距离优化其实就是机器学习中超参数优化，目前主流的机器学习超参数优化方法有群体智能优化算法、网格搜索（即穷举法） 、随机搜索算法、贝叶斯优化算法。但是群体智能优化算法先要提供非常多的初始样本点，并且其优化效率一般。网格搜索算法是将所有涉及的超参数进行组合，对每个组合进行建模与评价，最后选择评价最高的组合作为模型最终的超参数，这种方法需要经过长时间的计算才能获得最优的超参数组合。而随机搜索则是在超参数的分布中随机搜索超参数进行建模，它的缺点是容易错过一些最优超参数。贝叶斯优化方法要优于群体智能优化算法、网格搜索算法和随机搜索算法，因为它在尝试下一组超参数时，会借鉴之前的评估结果，省去了很多无用功。因此本文选取贝叶斯算法[9-10]（Bayesian Optimization） 作为DPC聚类算法的优化手段，利用贝叶斯算法预测出的较优[dc]值，驱动DPC算法选择出合适的聚类中心，提高DPC聚类算法的性能。

2 相关研究

2.1 DPC算法

密度峰值的聚类算法[11-12]（clustering by fast search and find of density peaks， DPC），该算法能够自寻簇中心，对任意类型、大小的数据集能够进行准确高效的聚类。DPC算法具有两个前提：

1） 峰值密度点（簇中心） 局部密度大于近邻围绕的局部密度。

2） 要使得不同簇中心之间的距离相对较远。

为了能够准确找到同时满足以上两个条件的簇中心，DPC算法引入了局部密度的定义。局部密度的计算如公式（1） 所示：

[ ρi=j≠if（dij-dc）]               （1）

假设数据点[ai]的局部密度为[ρi]，[dij]为[ai]到[aj]的距离，[dc]为两点间的截断距离。[f（x）]为逻辑判断函数，当[x]值小于0时[f（x）]判定为1否则[f（x）]判断为0，该函数表示为满足一定距离阈值数目[ai]的多少，数目越多值越大，密度越高。

高密度最小值计算如公式（2） 所示：

[δi=minj：pj>pi（dij）]               （2）

[δi]表示为高密度的最小距离为[ai]到[aj]距离最近并且局部密度大于[ai]的局部密度的距离。当[ai]为数据集中密度最大的点时[δi]的计算如公式（3） 所示：

[δi=maxj?c（dij）]             （3）

2.2 贝叶斯优化算法

贝叶斯优化算法（Bayesian Optimization，BO） 是一种基于黑盒的优化算法[13]，该算法的优化思路是首先生成初选解集合[x1，x2，x3，...xn]，也就是n个采样点，其次用目标函数[f（x）]分别计算以上样本点处的值，接着通过高斯回归过程来计算每一点处[fx]函数值的均值和方差，并且根据当前采样数据点集[D={（xn，f（xn）}]更新[pf（x）|D]的均值和方差计算采集函数[u（x）]，然后使用采集函数极大值[xn+1=argmaxxu（x）]确定下一个采样点。下一个采样点的函数值为[yn=f（xn+1）]，将该采样点加入原有集合中，不断重复直至迭代终止，最后从这些点集中找出[fx]函数值最大的点就是问题的最优解。

1） 采集函数的构建

构建采集函数[14]常用的方法有基于提升策略的PI，EI办法和置信边界策略方法。因为EI采集函数参数少，既整合提升的概率又体现不同的提升量，所以本文采用基于提升策略中的EI方法作为采集函数。已知对[n]个数据点进行探索，该点集中极大值函数按公式（4） 计算：

[f*n=max（f（x1），...，f（xn））]       （4）

现考虑下一搜索点[x]，如果下一搜索点[f（x）]值大于等于[f*n]，则该点处的极大值为[f（x）]否则为[f*n]。将加入新点后的改进值写成[f（x）-f*n+]（如果下一搜索点[f（x）]值大于等于[f*n]，则[f（x）-f*n+]等于正值[f（x）-f*n]，否则[f（x）-f*n+]为0），再计算所有[x]处的改进值的数学期望，并将数学期望最大的[x]点作为下一个探索点。期望改进函数如公式（5） 所示：

[EInx=Enf（x）-f*n+]           （5）

根據上述公式计算出[n]个采样点[x1，x2，x3，...xn]和函数值[y1，y2，y3，...yn].该期望采用高斯过程回归定义。假设在[xn]点的均值为[μ（x）]方差为[σ2（x）]，令[Z=f（x）]，根据期望定义能够得出公式（6） ：

[EIn（x）=-∞+∞Zf*n+12πσexp-（Z-μ）22σ2dZ]   （6）

化简为如公式（7） 所示：

[EIn（x）=-∞+∞（Z-f*n）12πσexp-（Z-μ）22σ2dZ] （7）

对公式（7） 进行换元可以得到公式（8） 如下所示：

[EIn（x）=μ-f*n（1-δf*n-μ/σ+σφf*n-μ/σ）]                            （8）

其中[δ（x）]为正态标准分布函数，若令[G（x）=μ-f*n]则有公式（9） ：

[EIn（x）=G（x）++σ（x）φG（x）σ（x）-G（x）δG（x）σ（x）]    （9）

因此由上述公式可以推导出[μ（x）]，[σ2（x）]均为[x]的函数，因此EI也是[x]的函数。为了能够优化目标函数[f（x）]因此通过最大化[EIn（x）]来得到新的评估点[xn+1]，计算如公式（10） 所示：

[xn+1=argmaxEIn（x）]               （10）

3 BO-DPC算法

3.1 主要思想

DPC在数据聚类方面具有很好的性能，但是截断距离[dc]值研究者凭借经验设定的，DPC算法不能完全发挥DPC算法的性能。因此本文选取贝叶斯算法来优化DPC聚类，利用贝叶斯算法预测出的较优[dc]值，驱动DPC算法选择出合适的聚类中心，提高DPC聚类算法的性能。获得最终的聚类结果。BO-DPC算法的流程图如图1所示。

当数据数量较多，类间距离不均匀时，试图依靠用户的经验来人工确定一个合适的[dc]值并取得较好的聚类效果是相当困难的一项任务，这也是阻碍DPC算法广泛应用的主要瓶颈之一。本文认为不应事先确定密度峰值聚类算法的这一项关键参数，而应在聚类过程中根据聚类的结果来不断对该参数寻优，直到算法逐渐收敛于使目标函数值最大化的全局最优截断距离[dc]值。首先创建截断距离[dc]值的寻参空间和生成寻优初选集合，轮廓系数Silhouette是簇的密集与分散程度的评价指标，它结合了内聚度和分离度两种因素，因为它可以用来在相同原始数据的基础上评价算法不同运行方式对聚类效果的影响，因此本文将Silhouette指标函数作为[f（x）]目标函数进行寻优。算法的最终目的在于优化[f（x）]指标值，使得[dc]值向最优的[dc]值慢慢靠近，因此希望采集函数每次评估的[dc]值都尽可能使得[f（x）]达到更大。通过采集函数[EI]进行构造，使得探索开发区域平衡，进而获取新的评估点[dc]，丰富[dc]集合。设置最大迭代次数为[N]，通过对原有[dc]值集合进行[N]次的迭代更新寻找最优[dc]值。最终找到使目标函数Silhouette值最大的[dc]值作为最优参数，然后用这个[dc]值完成后续的密度峰值聚类步骤。

3.2 算法步骤

4 实验的仿真与分析

4.1 实验数据

为测试BO-DPC算法的聚类效果，本文采用以下Aggregation、Flame、Jain、Spiral四种数据集进行实验对比，四种数据集实验数据见表3。

Aggregation、Flame、Spiral是二维数据集，Flame、Spiral在数据点个数上较少。Jain数据集为三维数据集在数据处理时需对Jain数据集维度进行降维。

4.2 实验评价指标

为验证BO-DPC聚类效果的有效性，本文选取了内部和外部评价指标进行分析，分别是Silhouette指标和F-measure指标。

1） Silhouette评价指标：

Silhouette遵循类的紧致性，用来描述目标自身所处的簇和其他簇之间的相似性。其范围为[-1，1]之间，Silhouette越大表明自身所在关系之间的匹配度越高，相反的与其他非自身相关簇匹配度越低。Silhouette的定义：对于聚类算法已经分成了很多类，对于目标[i]有[i?Ci]，[Ci]表示为第[i]个簇，就可以得到样本[i]在[Ci]类中与其他所有样本平均不相似度[a（i）]，计算如公式如（11） 所示：

[ a（i）=1Ci-1j?Ci，i≠jdij]             （11）

对于目标[i]有[i?Ck]，[Ck]表示为第[k]个簇。[b（i）]表示为到[Ck]类平均不相似度，计算如公式如（12） 所示：

[b（i）=mink≠i1Ckj?Ck，i≠jdij]         （12）

根据如上公式（11）、（12） 可以定义出Silhouette指标计算公式如（13） 所示：

[Sili=b（i）-a（i）max{a（i），b（i）}]             （13）

2） F-measure评价指标：

F-measure指标是结合了信息检索中准确率（ACC） 和查全率（Recall） 聚类算法的外部评价方法，ACC、Recall、F-measure评价指标计算公式如（14） 、（15） 、（16） 所示：

[  ACC=TP+TNTP+TN+FP+FN]           （14）

[Recall=TPTP+FN]               （15）

[F1-measure=2Precision?RecallPrecision+Recall]       （16）

TP表示两个数据样本在同一个簇的数量情况，TN表示两个非同类样本在两个簇中的数量情况。FP表示非同类数据样本在同一个簇的数量情况，FN表示两个同类样本分别在两个簇中的数量情况。如表2所示为以上四种参数的混淆矩阵（Pair Confusion Matrix）。

4.3 实验结果与分析：

本文在内存12G笔记本上采用python对BO-DPC算法和DPC算法进行实验仿真。通过四个数据集进行实验比对，根据实验结果BO-DPC聚类算法在内部评价指标Silhouette和外部评价指标F-measure上均优于传统的DPC算法。两种算法的评价指标如表5所示：

根据表5可以得出基于BO算法优化的DPC建立在Aggregation、Flame、Jain和Spiral数据集上的内部指标Sil和外部指标F-measure均有提升。在数据集Aggregation、Flame、Jain、Spiral中，BO优化后的DPC算法Sil指标相比于DPC算法提高提升了1.7%、1.3%、4.5%、3.3%。F-measure提升了3.3%、1.9%、2.2%、3.8%。Aggregation、Flame、Jain和Spiral聚类结果二维图分别如图2～图5所示：

由图2～图5四种数据集聚类二维示例图可以看出，本文BO-DPC算法和DPC算法都可兼顾到各点的密度和点间距的内部关系。可以准确地确定数据集类簇的数量和确定类簇中心点。但对于传统的DPC算法，相比于BO-DPC算法对簇边界的点容易造成误判，对大型簇的划分较为混乱。改进后的BO-DPC會对误判的簇边界点进行修正和划分合理的簇类。

综上所述BO-DPC 算法相对于DPC算法在处理不同大小的数据集都有较好的效果。通过BO算法在寻优空间进行迭代寻参，对DPC算法聚类结果进行修正，可以提升聚类效果。尽管BO-DPC算法效果提升不太明显，但是可以看出该算法在Aggregation、Flame、Jain、Spiral数据集上表现优于算法样本自身分布，体现了BO-DPC适应性较强。

5 结束语

传统DPC聚类算法需要指定截断距离，本文提出采用贝叶斯算法提升DPC聚类性能，通过在寻优空间计算迭代找到适应度最优的[dc]值，使BO-DPC算法聚类效果达到最优。通过实验分析BO-DPC算法相比于传统的DPC算法在内部指标Silhouette和外部评价指标F-measure当中都有更优异的表现。接下来研究重点如何进一步提升DPC聚类算法的性能是后续工作的重点。

参考文献：

[1] 胡明，唐东凯，李芬田，等.不确定聚类中距离计算方法综述[J].长春工业大学学报（自然科学版），2017，29（5）：477-483.

[2] Xu R，Wunsch D.Survey of clustering algorithms[J].IEEE Transactions on Neural Networks，2005，16（3）：645-678.

[3] Zhao W L，Deng C H，Ngo C W.K-means：a revisit[J].Neurocomputing，2018，291：195-206.

[4] Ester M，Kriegel H P，Sander J，et al.A density-based algorithm for discovering clusters in large spatial databases with noise[C]//kdd，1996，96（34）：226-231.

[5] Rodriguez A，Laio A.Clustering by fast search and find of density peaks[J].Science，2014，344（6191）：1492-1496.

[6] Liu Y H，Ma Z M，Yu F.Adaptive density peak clustering based on K-nearest neighbors with aggregating strategy[J].Knowledge-Based Systems，2017，133：208-220.

[7] Seyedi S A，Lotfi A，Moradi P，et al.Dynamic graph-based label propagation for density peaks clustering[J].Expert Systems With Applications，2019，115：314-328.

[8] Xie J Y，Gao H C，Xie W X，et al.Robust clustering by detecting density peaks and assigning points based on fuzzy weighted K-nearest neighbors[J].Information Sciences，2016，354：19-40.

[9] Shahriari B，Swersky K，Wang Z Y，et al.Taking the human out of the loop：a review of Bayesian optimization[J].Proceedings of the IEEE，2016，104（1）：148-175.

[10] Ghahramani Z.Probabilistic machine learning and artificial intelligence[J].Nature，2015，521（7553）：452-459.

[11] Jiang J H，Tao X，Li K Q.DFC：density fragment clustering without peaks[J].Journal of Intelligent & Fuzzy Systems，2018，34（1）：525-536.

[12] Jiang J H，Hao D H，Chen Y J，et al.GDPC：gravitation-based density peaks clustering algorithm[J].Physica A：Statistical Mechanics and Its Applications，2018，502：345-355.

[13] Williams C K，Rasmussen C E.Gaussian processes for machine learning[M].Cambridge，MA：MIT press，2006.

[14] Hoffman M，Brochu E，De Freitas N.Portfolio Allocation for Bayesian Optimization[C]//UAI，2011：327-336.

【通聯编辑：谢媛媛】