面向学生成绩分析的高效关联规则挖掘算法研究

周日辉

摘要：数据挖掘技术是在大数据环境下，通过利用关联规则挖掘等技术方法，进行知识发现，其核心过程是挖掘算法在起关键作用。文章分析了关联规则挖掘技术原理，以学生成绩作为数据样本，对其算法进行分析，探讨算法优化思路，提出高效的算法改进方案并验证。为进一步利用关联规则挖掘技术探索教育领域的数据挖掘应用研究打下坚实的基础。

关键词：数据挖掘；关联规则；学生成绩；算法；教育

中图分类号：TP399      文献标识码：A

文章编号：1009-3044（2022）30-0048-03

开放科学（资源服务）标识码（OSID）：

1  关联规则挖掘概述

关联规则挖掘[1-2]是一个旨在发现一大组数据项之间隐含关系的数据挖掘技术。通过关联规则挖掘过程，最后得到的分析结果是一系列形如“P -> Q”的蕴涵式，这个蕴涵式也称之为关联规则。式子中的“P”和“Q”分别称为规则前件和规则后件。令 I ={i1，i2，i3，…，in}，是一组项目集合，另外 Trans = {t1，t2，t3，…，tn}是所有事务的集合，某个事务tj，其包含的项集都是I的一个子集。在关联分析过程中，含有零个以上数目项目的集合叫作项集，则有“k-项集”的表示形式，k表示项集中项目的个数。如果项集P是事务tj的子集，则说明项集P包含于事务tj中。项集一个重要称为支持度计数σ（P），其含义是指在所有的事务项目中，项集P是多少个事务的子集。其定义可以表示为：

支持度计数[3]  σ（P）=|{ tj| P ?tj，tj∈Trans}|；对于关联规则挖掘结果的某一条蕴涵式“P->Q”，其中项集P和项集Q的关系为P∩Q= {φ}，关联规则质量的评估标准可以用“s”（支持度）和“c”（置信度）来衡量。

支持度[3] s（P->Q） = σ（P∪Q） / N （N为事务集合中事务项的总数）；

置信度[3] c（P->Q） = σ（P∪Q）  / σ（P）；

关联规则挖掘可以定义为，在给定的事务集合“Trans”上，搜索发掘支持度超过支持度阈值并且置信度也超过置信度阈值的所有形如“P->Q”的规则。

关联规则挖掘工作主要分为两个部分，第一个任务是从项目集合“I”中发掘满足大于支持度阈值的所有项集，称之为频繁项集[4]（关联分析中用到的关键概念），此外，根据项集的项数来命名频繁项集，如包含K项的项集，如果满足支持度阈值，则称之为“频繁K-项集”，得到所有的频繁项集，是挖掘关联规则的先决条件；第二个任务是在得到的频繁项集中，通过组合不同的规则前后件演化成不同规则，所有满足大于置信度阈值的规则称之为强规则，这也是关联挖掘的最终结果。

2  关联规则挖掘算法

2.1 Apriori算法描述

Apriori算法[5]是解决关联规则挖掘工作的第一个算法，算法根据关联规则挖掘的两个任务而设计，频繁项集的产生及规则的产生，在实践过程中会发现前者的计算开销远大于后者。

在频繁项集产生的任务中，算法使用一种称作逐层搜索的迭代方法，即“（K-1）-项集”是用于搜索“K项集”的前提条件。算法开始，找出包含所有“频繁1-项集”的集合，该集合通过两两结合的方式生成称之为“候选2-项集”的集合，这一步骤我们称之为“连接步”。由于从“候选K-项集”集合生成“频繁K-项集”集合的过程，需要把每个候选集和每条事务进行对比，如此计算开销呈指数级增长，为减少计算开销，一方面需要减少“候选K-项集”的数量，这一步骤称之为“剪枝步”。应用的是Apriori算法的核心思想，称为“先验原理”[5]，即：如果一个项集是频繁的，那它的所有子集也一定是频繁的，反过来同样成立。

算法得到包含所有频繁项集的集合后，同样使用逐层的方法产生规则，规则后件项的数目对应当前层数。针对某一个频繁项集，后件只有一项的候选规则首先被提取，检测其置信度产生高置信度规则，然后两两合并后件而生成新的候选规则，例如由频繁项集{a，b，c}产生的两个高置信度规则（a，b->c）及（a，c->b），合并成候选规则（a->b，c），对此候选规则再进行置信度检验，从而确定其是否成为强规则，以此类推直至不再产生新的候选规则。为减少候选规则数量，同样利用类似“先验原则”的定理进行剪枝，即如果规则“X->（Y-X）”不满足置信度阈值，则规则“X'->（Y-X'）”一定也不满足置信度阈值，其中X是X的子集。

2.2 Apriori算法的改进

本文针对高校学生成绩开展关联规则挖掘以探索高校育人规律，以广东茂名幼儿师范专科学校历年的学生数据作为原始数据。为保证数据挖掘质量与目标，选择的原始成绩数据的学生应为相同或相近专业，成绩数据应包含学生相同学期区间的成绩项，成绩数据中的学生年级可以不同，但应为相同学年制。通过数据预处理，对原始数据存在的空值、非法记录等异常情况作清洗处理，以及数据格式和数据类型的转换。数据类型转换主要是由于成绩数据为连续型属性，为适应关联挖掘算法的应用，需要对成绩数据进行“离散化”[6]处理，即分等级。

对Apriori算法进行改进的方法，就是在算法执行频繁项集挖掘任务的过程中，通过纵、横两个维度对事务集的质量及数据量进行调整，其进行改进思想如下：

（1）纵向。对于成绩分数在某个等级所占比例（根据实际情况设置阈值参数）过高，或者成绩集中分布在较少等级数（根据实际情况设置阈值参数）的科目，在算法为发现“频繁1-項集”时第一次扫描全局事务集后，从事务集中被排除或被标记，在整列数据被剔除或被标记的同时，该科目亦将不会产生的“频繁1-项集”，如此一方面避免产生较多无分析价值的交叉支持模式[7]，另一方面也减少了需要扫描的事务集数据量，如此在提高挖掘的质量及效率上做贡献。

（2）横向。根据Apriori算法的先验原理，一个频繁项集的所有非空子集也一定是频繁的，反之，一个非频繁项集的超集也一定是非频繁的。由此进行如下推论，如果一个事务包含的所有 “K-项集”都是非频繁的，即该事务不包含任何“频繁K-项集”，那么它所有的“（K+1）-项集” 也一定是非频繁的（“（K+1）-项集”是“K-项集”的超集），即其一定不会包含任何“频繁（K+1）-项集”，如此迭代，该事务将不再包含任何“频繁L-项集”（L>K）。根据此推论，当算法完成“频繁K-项集”的统计后，不包含任何“频繁K-项集”的事务将不会为统计“频繁L-项集”（L>K）的工作做任何贡献，所以，可以将该事务从事务集中删除（标记），即为得到“频繁L-项集”（L>K）扫描全局事务集时不再扫描该事务，从而减少需要扫描的事务集数据量。这是一种逐层减少事务数据量的方式，是对Apriori算法先验原理的灵活运用。

2.3 改进算法伪代码

算法： New_Apriori

输入：事务集T，项目集合I，支持度阈值minSup，成绩等级比例阈值overSup，成绩等级数量阈值minGrd。

输出：T中的频繁项集。

方法：

（1）  k = 1

（2）  for 每个项i∈I

（3）  { if（σ（i）>= N*overSup ∨ testGrade（i ， minGrd）==true）（测试该项所占比例是否过高，和该科目的成绩等级分布是否过窄）

（4）  { I.deleteItem（i）        （删除该项）

（5）  T.deleteColumns（i）     （事务数据集删除该数据列）

（6）  }

（7）  else if（σ（i） >= N*minsup）

（8）  Fk.add（i）   （发现所有频繁1-项集）

（9）   }

（10）  repeat

（11）  k = k+1

（12）  Ck = apriori_gen（Fk - 1）     （产生候选项集）

（13）  for 每个事务t∈T

（14）  { Ct = subset（Ck，t）      （识别包含在t的所有候选集）

（15）  for 每个候选项集 c∈Ct

（16）  {σ（c）  = σ（c） + 1    （项集c增加支持度计数）

（17）  }}

（18）  Fk  = {c|c ∈Ck ∧σ（c） >= N*minSup}

（19）  CompressInstances（T，Fk）    （事务集的压缩，在事务集T中删除不包含任何频繁项集的事务）

（20）  until Fk = ?

（21）  Return =∪Fk

算法： CompressInstances函数，通过排除不包含任何频繁K-项集的事务进行事务集合的压缩

输入：事务集T，频繁K-项集集合itemSets

输出： 压缩后的事务集合

方法：

（1）  function CompressInstances（T，itemSets）

（2）  for i = 0--> T.numInstances（）  do

（3） enu <-- itemSets

（4） containItemSet <--false

（5） while enu.hasMoreElements（）= true  do

（6）  if enu.nextElement（）.containedBy（T.instance（i））  do   （判断当前频繁K-项集是否被第i个事务包含）

（7）   containItemSet <-- true

（8）  break

（9）    end if

（10） end while

（11）  if containItemSet = false  do

（12）  T.delete（i）   （事务集删除第i个事务）

（13）  end if

（14） end for

（15）  end function

New_Apriori算法有两个主要过程，第一个过程是算法的第1-9步，在检测所有的频繁1-项集时，删除成绩等级分布异常的数据列（科目）。第二个过程是算法第10～21步，在每一次迭代的过程中，通过支持度计数的方式发现频繁k-項集，并对事务集进行检测，在事务数据集中排除（标记）不包含任何频繁k-项集的事务，这通过CompressInstances函数实现。通过这两步，避免了在挖掘结果中产生冗余或交叉支持规则，也有效地降低了Apriori算法需要扫描的事务数据量，从而大大提高算法的性能。

3  改进算法的验证

对于使用数据挖掘算法得到的关联规则，建立一种广泛接受并合乎客观实际的评估标准尤为重要，客观兴趣度度量是利用数据驱动评估规则质量，客观兴趣度分析是在支持度与置信度之外，考究规则前后件的“相关性”，使用“提升度值（lift）”[8]进行度量，亦被称作“兴趣因子”，它计算关联规则的置信度与规则后件的支持度之间的比率，即：

lift（P->Q）= c（P->Q） / s（Q）

提升度值（lift）参数的意義在于，在置信度已经考虑了规则前件支持度参数的基础上，再考虑规则后件支持度进行概率计算，当其值等于1，说明P与Q是独立事件，当其值大于1，P与Q存在正相关性[9]，值小于1则存在负相关性，存在正相关性且其值越大则代表规则前后件有积极的依赖关系或因果关系，而负相关性则代表这两个事件有消极的影响关系，在实际应用中，前后件呈正相关性或负相关性的，尤其是正相关而且其提升度值越大的关联规则是更值得关注的。

对改进算法的验证，首先选取学校200名学生80项科目的成绩作为数据样本，运行改进算法及原算法，对比两者的工作情况进行验证。对两算法所获得的高支持度高置信度的规则进行“客观兴趣度”的质量评估，通过在设定相同支持度阈值及置信度阈值的情况下，对比两算法挖掘出“相关性”高的规则占总规则数量比例的高低。

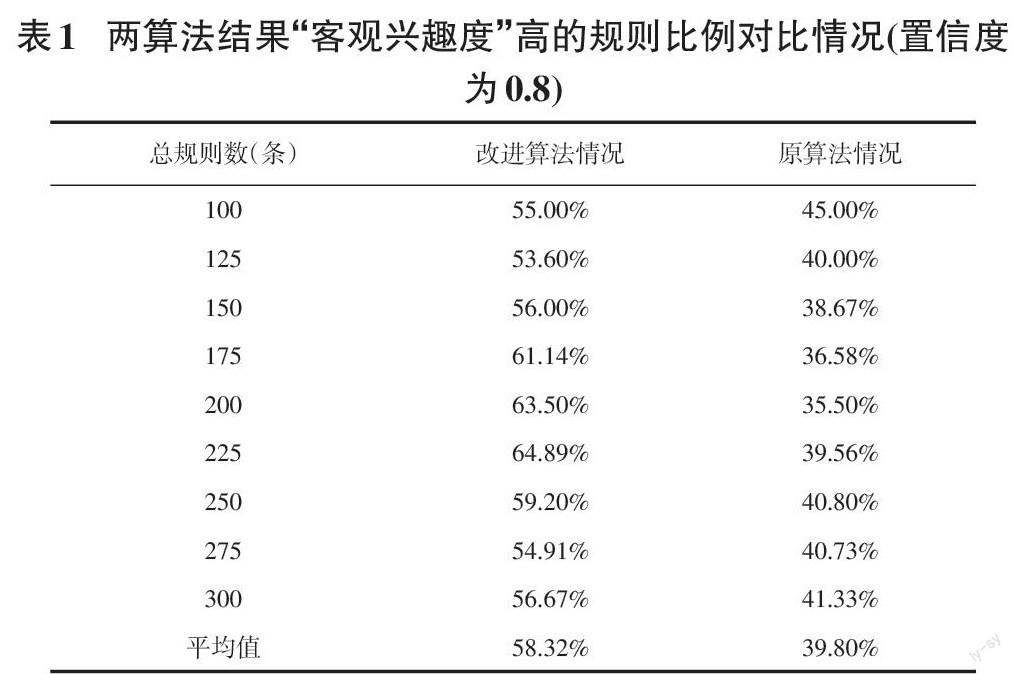
在挖掘过程中，为保证规则质量，不断调整算法参数以达到最合理，设置支持度阈值上下限分别为0.6及0.3，当置信度阈值设置为0.8时，随着设置挖掘的最优规则总数量的变化，两个算法的挖掘结果中，“客观兴趣度”高的规则比例对比情况如表1所示，当置信度阈值为0.9时的情况类似。

接下来，对比两算法的运行效率，设置相同的支持度阈值情况，设置挖掘的最优规则数量为100，不断改变置信度阈值，每设定一个置信度阈值，运行算法10次取平均值，两算法运行时间的对比情况见图1。

以上实验是选取学校真实成绩作为准备数据样本，为进一步验证改进Apriori算法设计的效果，现保持与上述数据样本的学生范围、科目范围不变，编写随机函数以生成成绩值的方式，生成准备数据样本。运行随机函数10次，生成10个随机准备数据样本，针对每个样本运行改进算法及原算法，参数设定支持度阈值上限为0.3，支持度阈值下限为0.1，由于数据样本为随机数值，故降低支持度阈值要求，以保证挖掘数量，置信度阈值为0.8，挖掘最优规则数量为100，运行时间是运行算法10次取平均值，两算法运行情况对比如表2所示。

以上实验结果显示，在10个随机数据样本的实验中，改进算法产生的高客观兴趣度规则的平均比例为39%，高于原算法29%，改进算法运行的平均时间为3859（ms），效率高于原算法27356（ms）。实验结果与以真实成绩作为数据样本的实验结果基本吻合。

4  结束语

综上所述，通过对关联规则挖掘算法的改进，在效率和挖掘质量上都有一定提升，在效率上的提升较为明显。原算法在设计上是为迎合不同挖掘需求，在使用上具有普适性。本文的算法改进方案是针对学生成绩数据挖掘或与此应用情况类似的场景而设计，挖掘过程比原算法更高效，为通过对学生成绩等教育资源数据进行数据挖掘，进一步构建完整的系统应用提供有力的技术支持。

参考文献：

[1] 康君.教育数据挖掘服务平台的设计与实现[D].济南：山东师范大学，2016.

[2] Sin K，Malaysia O U，Muthu L，et al.“application of big data in education data mining and learning analytics - a literature review”[J].ICTACT Journal on Soft Computing，2015，5（4）：1035-1049.

[3] 李忠，安建琴，刘海军，等.关联挖掘算法及发展趋势[J].智能计算机与应用，2017，7（5）：22-25.

[4] 李强.数据挖掘中关联分析算法研究[D].哈尔滨：哈尔滨工程大学，2010.

[5] 赵峰，刘博妍.基于改进Apriori算法的大学生成绩关联分析[J].齐齐哈尔大学学报（自然科学版），2018，34（1）：11-15.

[6] 谭诚.基于数据挖掘的义务教育绩效考核分析系统的设计与实现[D].长沙：湖南大学，2016.

[7] 琚安康，郭渊博，朱泰铭，等.网络安全事件关联分析技术与工具研究[J].计算机科学，2017，44（2）：38-45.

[8] 陈建尧.云计算下的一种关联挖掘算法的研究[J].科技通报，2018，34（7）：188-192.

[9] Pang-Ning Tan，Micheal SteinBach，Vipin Kumar. Introduction to Data Mining[M]. 北京：人民邮电出版社，2011：201-303.

【通联编辑：唐一东】