基于监测数据的斜拉索模态参数变异性分析
2022-05-30周海俊刘俊辉杨夏李婧超张超东孙利民
周海俊 刘俊辉 杨夏 李婧超 张超东 孙利民
摘 要:基于某大跨斜拉橋 5根拉索1年的加速度和温度监测数据,系统分析了在良好天气和暴雨天气下拉索模态参数和索力的变化特征.使用快速傅里叶变换和随机子空间法识别模态频率和阻尼比.对比发现,暴雨天气下拉索振幅大,低阶模态的振动明显,模态阻尼比在两种天气下有一定的差异性.使用频率法计算得到了各拉索连续一年的索力值,其为非平稳时间序列,且具有年和日周期性的波动.索力-索温关系分析表明,各拉索索力-索温的关系各 不同,同一根拉索在不同温度范围内的索力-索温关系也可能存在很大的差异.使用半功率带 宽法计算得到了各拉索连续一年的阻尼比,得到了自相关函数和其自功率谱,并拟合得到了阻尼比的边缘概率密度分布函数.分析表明,各拉索阻尼比具有时长为1d、12h、6 h的周期成分,其边缘概率密度函数可用Burr分布描述.拉索的阻尼比受环境温度的影响较小,受车辆荷 载的影响较大.
关键词:拉索振动;监测数据;模态参数;索力;温度效应;变异性分析
中图分类号:U448.27,U448.14 文献标志码:A
Modal Parameter Variance Analysis of Stay Cable Based on Monitoring Data
ZHOU Haijun1,LIU Junhui2,YANG Xia1,LI Jingchao3,ZHANG Chaodong1?,SUN Limin4(1.Institute of Urban Smart Transportation & Safety Maintenance,Shenzhen University,Shenzhen 518060,China;
2.Shenzhen Water Group Co,Ltd,Shenzhen 518060,China;
3.College of Mathematics and Statistics,Shenzhen University,Shenzhen 518060,China;
4.State Key Laboratory for Disaster Reduction in Civil Engineering(Tongji University),Shanghai 200092,China)
Abstract:The time-varying characteristics of cable modal parameters and cable tensions under good weather and heavy rain are systematically analyzed based on the one-year acceleration and temperature monitoring data of five cables on a long-span cable-stayed bridge.The modal frequency and damping ratio are derived using the fast Fourier transform(FFT) and stochastic random identification(SSI) method.It is found that the cable vibratesgreatly under wind and rain conditions.The low-order mode dominates the vibration,and the modal damping ratio has certain differences in the two circumstances.The tension force of each cable throughout the year,derived using the frequency method,is a non-stationary time series and has annual and daily periodic fluctuations.The correlation analysis of the cable tension and temperature shows that the correlation between the two of each cable is different,even differs on the same cable in different temperature ranges.The half-power bandwidth method is used to calculate the damping ratio of each cable for one year,the autocorrelation function and its self-power spectrum are obtained,and the edge probability density distribution function of the damping ratio is also obtained by fitting.The analysis shows that the damping ratio of each cable has the periodic components of1day,12hours,and6 hours,and its edge probability density function can be described by Burr distribution.The damping ratio of the cable is less affected by the ambient temperature but more by the vehicle load.
Key words:cable vibration;monitoring data;modal parameters;cable tension force;temperature effects;vari-ance analysis
斜拉桥具有适应性强、跨度大、桥塔和索面造型 优美多变等特性而得到了广泛应用,但其主要承重构件斜拉索易于受到外界环境因素激励而产生振动.斜拉索的大幅振动不仅会影响桥梁的安全和舒 适性,还会引起索梁锚固区出现疲劳裂纹、拉索保护 层脱落等病害[1-2].受腐蚀、疲劳等病害而损伤严重的斜拉索可能会突然失效并引发桥梁的坍塌 [3-4],典 型如意大利莫兰迪桥及我国台湾南方澳跨港大桥.因此,极有必要采用桥梁结构健康监测(SHM)系统[5]对拉索的振动及其状态进行监测.拉索的振动监测一般使用加速度计记录加速度时程数据,通过加速度数据计算索力和阻尼比[6-8].
桥梁状态的异常变化必然会导致索力重分布,而索力数据易于获得[9-10],因此索力数据为桥梁损伤的监测提供了重要的依据.Hua和Ni等[11]以及Li和Wei等[12]都通过索力分布的变化,成功地识别了桥梁的损伤.索力变化会受到环境因素如温度、风和车 辆荷载等影响[13-14].已有研究表明由环境因素,尤其是温度的影响[15-16],引起的索力变化可能会远大于桥梁损伤引起的索力变化.Liu和Huang等人[17]通过索力和温度的线性拟合,以考虑温度对索力的影响.Zhou和Ni等人[18]通过使用反向传播神经网络技术,建立了损伤敏感模态特性与温度之间的相关性模型,以消除温度的影响.Chen和Wu等[19-23]通过确定有效温度,研究了拉索温度、梁温度和塔温度对索力的影响,然后通过经验模式分解(EMD)的方法去除有效温度对索力的影响,并通过索力残差确定损伤 阈值.阻尼比直接反映拉索的耗能能力[24],是拉索的基本动力性能参数.对于安装有阻尼器的斜拉索,拉索阻尼比的大小变化可为斜拉索上阻尼器的状态评 估提供参考,指导阻尼器的更换维修或参数调整.此 外,在各类阻尼器的设计中,阻尼比是减振效果检验中非常重要的指标参数[25].因此,对斜拉索的阻尼比进行实时的监测和分析也具有十分重要的意义.
本文研究了国内某大型斜拉桥健康监测系统所采集的5根具有代表性的斜拉索1年的振动加速度和温度数据,研究成果可为桥梁拉索构件状态评估 提供重要参考.
1某斜拉桥概况及其健康监测系统
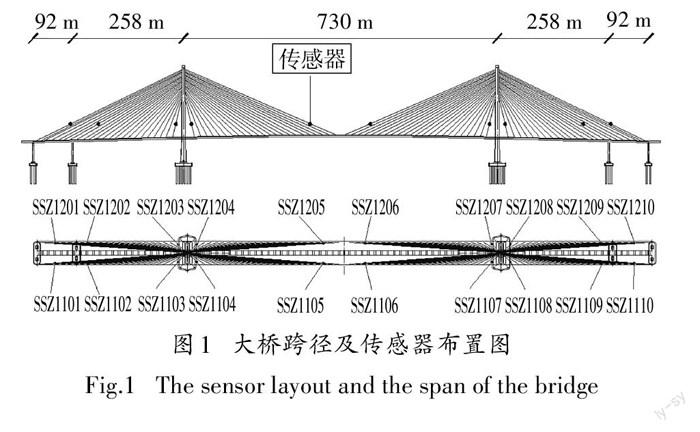
图1所示为某全漂浮体系斜拉桥,桥跨布置为(92+258+730+258+92)m=1430m,采用双索面上下游对称布置,每个索面 48对斜拉索,全桥共计96对(192根)斜拉索.
大桥安装有健康监测系统,其中20根拉索安装有加速度和温度传 感器,编 号分别为SSZ1101~ SSZ1110、SSZ1201~SSZ1210,其位置如图1所示.传感器使用特定的夹具安装在拉索上,采样频率为50Hz.该斜拉桥在横桥向和纵桥向均对称布置,因此仅 选取具有代表性的半跨1个索面 5根拉索SSZ1101~ SSZ1105的1年的监测数据(2012年8月1日至2013年8月1日).5根斜拉索相关参数见表1.
5根拉索可大致分为长索(SSZ1101、SSZ1102、SSZ1105)和短索(SSZ1103、SSZ1104)两类.由于文章 篇 幅所限,本文以下取 长索SSZ1102和短索SSZ1103两根拉索的监测数据为例重点阐述.图2所示为两拉索加速度时程,可见在2012年8月8 日、2012年12月29日、2013年4月6 日、2013年6月7 日、2013年7月5 日的加速度幅值都明显大于日常加速度幅值,长索SSZ1102在2013年6月7 日的加速度幅值更是高达3m/s2.
进一步分析加速度幅值较大的时间段对应的天气情况,如表2所示,该时间段均为风雨天气或台风 作用期,表明可能是因为风雨共同作用导致上述大幅振动现象.
2 不同天气拉索振动特性差异性分析
为比较拉索在不同天气下的振动模态参数,截 取良好天气情况下(6月4 日的08:00—6月5 日02:00时间段,天气状况为:多云,风力3级,温度21~26℃)和暴雨期间(2013年6月7 日至6月8 日,天气状况为:暴雨,台风 5~6 级,温度20~24℃)各根拉索的加速度进行对比分析.
采用快速傅里叶变换对拉索加速度进行分析.图3为拉索SSZ1102和SSZ1103的加速度频谱图.此时SSZ1101~SSZ1105 号拉索最明显的振动模态频率分别为:2.535Hz(第8阶)、2.722hz(第7阶)、17.47Hz(第13阶)、17.25 Hz(第13阶)、3.059Hz(第10阶).
图4为拉索在2013年6月7 日至8 日暴雨期间的加速度时程曲线,可见在6月7 日的08:00—8 日02:00时间段内加速度幅值较大,当天 SSZ1101~SSZ1105 号拉索的振动加速度幅值分别为:2 542mm/s2、2938 mm/s2、900mm/s2、843mm/s2、2636 mm/s2.特别地,在6月7 日的16:00—20:00时间段内各拉索加速度幅值均出现一个下凹谷底,这可能是因为热带气旋中心通过桥址风速减小所导致.
截取风雨天气(6月7 日的08:00—6月8 日02:00时间段)时加速度时程,对其进行快速傅里叶变换频 谱分析,其中拉索SSZ1102和SSZ1103的計算结果如图5所示.SSZ1101~ SSZ1105 号拉索最明显的振动模态频率分别为1.895Hz(第6阶)、2.722hz(第7阶)、3.903Hz(第3阶)、3.859Hz(第3阶)、2.134Hz(第7阶).分析表明,各拉索低阶部分的模态频率所对应的频谱图纵坐标振动幅值大于高阶部分的模态频率对应的振动幅值,尤其是长索(SSZ1101、SSZ1102、SSZ1105)更为明显.
进一步计算得到SSZ1101~SSZ1105 拉索在暴雨 天气和良好天气两种时间段的加速度频谱纵坐标最大幅值比值分别为53、100、3.0、3.7、29,可见风雨作用下各拉索加速度频谱图中的纵坐标最大幅值均有明 显的增加,尤 其是 长索(SSZ1101、SSZ1102、SSZ1105)增幅达数十甚至上百倍.
采用随机子空间算法进一步分别求得在风雨天气和良好天气情况下SSZ1101~SSZ1105 号拉索的各阶模态的振动频率和阻尼比[5,26],其中拉索SSZ1102和SSZ1103的计算结果如图6所示.结果表明,长索和短索的模态阻尼比在良好天气时和风雨天气时有一定的差异性.短索(SSZ1103、SSZ1104)模态阻尼比在风雨天气下整体较良好天气下小.
在风雨环境下,长索的阻尼比随着频率的增大整体呈现上升趋势,对于短索其阻尼比随频率变化波动较大但无明显的趋势,分布较为离散.而在良好的天气环境中无论是长索还是短索,阻尼比随频率的变化波动都不大.风雨环境下拉索振动时各阶模态阻尼比的变化大于良好天气环境下各阶模态阻尼比的变化.在风雨环境下长索最大阻尼比为0.51%,短索最大阻尼比为3.78%;良好环境下长索最大阻尼比为0.47%,短索最大阻尼比为1.29%.
综上,在风雨条件下长索大部分低阶模态阻尼比降低,高阶模态阻尼比增加;短索大部分模态阻尼比有所增加.需要指出的是,本文中识别的阻尼比包含了各种因素的影响,包括拉索所受的外界激励和自身振动幅值的影响.在风雨天气时长索低阶模态阻尼比的降低与其大幅振动互为驱动因果.不同天气时拉索的加速度幅值及根据频谱图中最大振幅对应的振动模态阻尼比如表3、表4所示,可见长短拉索在风雨天气情况下加速度幅值遠大于良好天气情况下的振动幅值,阻尼比的变化规律也与上述推断一致.
3 频率及索力变化分析
本文采用频率法计算索力,为简化起见采用张紧弦理论计算公式[6]:
式中:H为索力;n为拉索自振频率的阶数;fn为拉索第n阶自振频率;L为计算索长;ρ为拉索的线密度.
由于拉索频率和索力有式(1)所示的明确关系,本文重点以索力来阐述,可反映拉索频率差异性.以SSZ1102 号拉索的加速度时程为例阐明索力计算过程.先对加速度数据进行快速傅里叶变换求得拉索振动频率.由于拉索第八阶模态频率在各时间段内 幅值较大且稳定出现,因此被用于计算索力.取加速度时长为1200s、步长10s 循环计算可得到连续时间段内的索力变化值.图7所示为计算得到的两根典型拉索2012年8月1日 —2013年8月1日的索力变化值.
由图7可见,索力以日为基本周期波动,这主要是由于温度、车辆荷载和风的日变化效应所致,平稳 性检验(ADF)结果表明该时间序列非平稳.
结果显示,SSZ1101~SSZ1105索力变化量占平 均索力的比例分别为2.70%、3.94%、3.51%、4.94%、2.62%,均小于索力平均值的5%.可见该桥拉索索力主要由恒载索力控制.图7表明拉索索力的变化和温度有很大的相关性.2012年8月至2013年8月期 间拉索SSZ1102的温度如图8所示,可见全年索温的变化范围为47℃,平均温度为17℃.索温与索力存在相同的变化趋势,平稳性检验(ADF)结果也表明索温时间序列为非平稳.
表5给出了各拉索的索力和索温的线性相关系数,可见各拉索索力与索温的线性相关系数差异很大.为了进一步分析索力与索温之间的关系,图9给 出了拉索的索力和索温的散点图.
表5显示 SSZ1102和SSZ1105的索力-索温关系都表现出线性正相关,但前者的线性相关性(相关系数0.815)明显强于后者(相关系数0.650).其余三根索索力和索温整体表现为负相关,其中SSZ1103(见图9(b))的索力和索温在温度低于30℃时表现出线 性负相关,但当温度超过30℃时呈线性正相关,且 SSZ1103的线性关系明显强于SSZ1104.由此可见,不同拉索索力和索温的相关关系是不一样的,甚至同一根拉索在不同的温度范围内,其索力与索温的关系也不一样,这可能与主梁不同位置在温度作用下的变形不同有关.
4阻尼比变异性分析
本文采用半功率带宽法计算拉索的模态阻尼比[27]:
式中:ξ为阻尼比;f为共振频率;fL和fH是反应振幅等于共振振幅乘于1/ 2时的前后两个频率.以60min的加速度数据计算拉索阻尼比,以步长为1min 连续 计算得到持续变化的阻尼比值.由前述可知,在这 5根拉索中,长索以第8阶模态振动为主,短索以第2阶模态振动为主,因此本文中长索计算第8阶模态阻尼比,短索计算第2阶模态阻尼比.
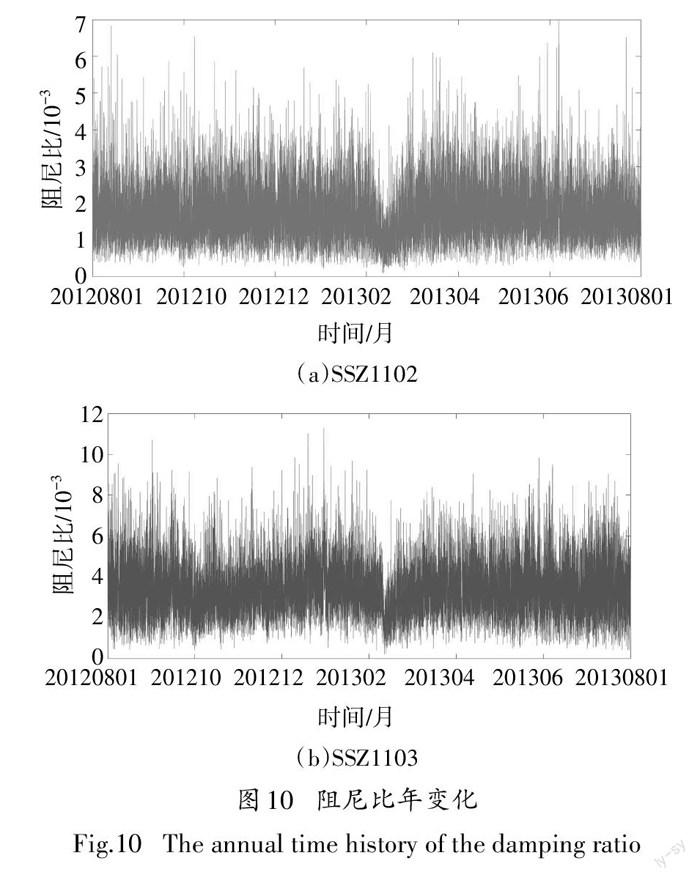
图10所示为拉索SSZ1102、SSZ1103在2012年8月1日至2013年8月1日期间的阻尼比,可见在一整年的阻尼比变化中,在2013年2月与3月之间存在一个较小的“缺口”,该区间的阻尼比明显比其他时间段小得多.该缺口对应的时间段刚好为2013年2月1日至2月18 日的春节假期,很可能与春节期间 车辆荷载的变化有关.
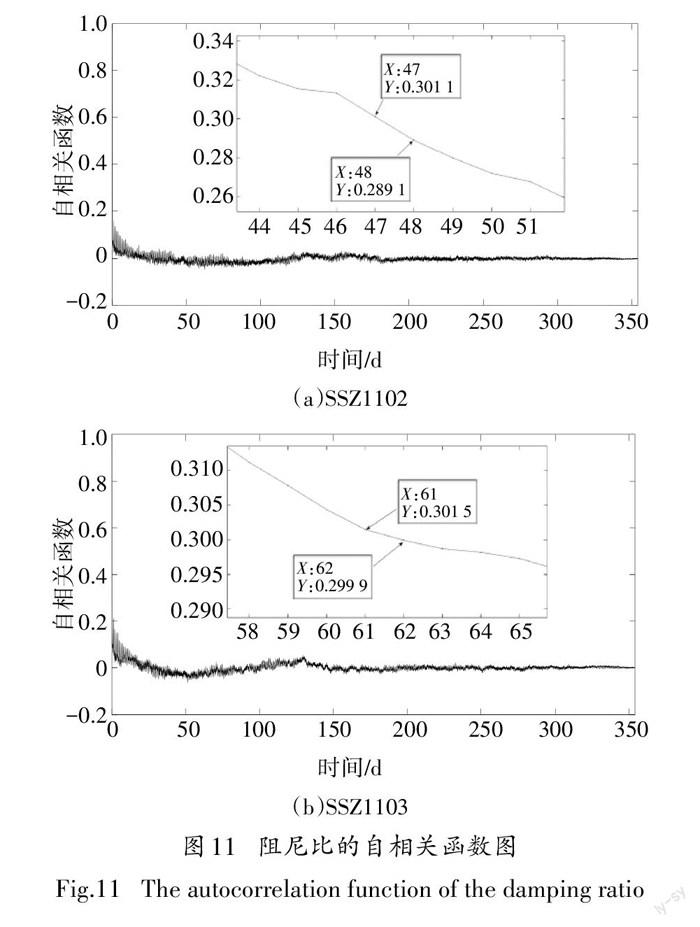
分别对长索和短索一整年的阻尼比时变数据计算其自相关函数,如图11所示.一般认为,相关系数低于0.3为相关性较低甚至是不相关.故在图中标出了相关性衰减至0.3处的点以及所对应的时间.从图11中我们可以看到阻尼比的自相关系数分别在延迟 47 min、61min 后降到0.3以下,之后继续减小,最后在0附近波动.
图12所示为SSZ1102和SSZ1103号拉索阻尼比数据的自功率谱,可以看出该组数据存在分别为1d、12h、6 h的变化周期,3个周期的强弱随时间的减少而衰减.
如图13所示,统计分析拉索阻尼比的边缘概率密度分布函数发现,其均符合 Burr分布.SSZ1101~ SSZ1105 五根拉索阻尼比结果汇总如表6所示,可见 拉索振动模态阻尼比的均值低于0.5%的减振目标 要求.短索2阶模态阻尼比的均值和标准差均大于长索8阶模态阻尼比的均值和标准差.此外,阻尼比的标准差为均值的1/3左右,表明服役环境下测得的拉索阻尼比离散性极大.此外进一步的分析表明拉索的阻尼比受环境温度的影响非常小,此处不再 赘述.
5结论
1)风雨天气环境下,斜拉索低阶模态频率的振动更为明显,斜拉索振动的加速度幅值远大于良好 天气环境下,长索尤为明显.与良好天气环境相比,在风雨条件下长索的低阶模态阻尼比降低,高阶模态阻尼比增大,短索各模态阻尼比均有所增大.
2)索力存在明显的日和年周期变化.大桥不同位置拉索的索力与索温的关系不同,甚至是同一根拉索,在不同温度范围内索力和索温的关系也可能存在很大的差异.
3)拉索阻尼比受温度影响很小,但与车辆荷载 存在着相关性.阻尼比的自相关函数随时间间隔增加迅速变小为0,中间存在着1d、12h、6 h的变化周期.
4)拉索阻尼比的概率密度函数服从Burr分布,其均值变化范围为0.18%~0.35%,标准差为0.065%~0.11%,对应的变异系数稍大于0.3.
参考文献
[1]WU Q,TAKAHASHI K,NAKAMURA S.Non-linear response of
cables subjected to periodic support excitation considering cable loosening[J].Journal of Sound and Vibration,2004,271(1/2): 453-463.
[2]LILIEN J L,DA COSTA A P.Vibration amplitudes caused by
parametric excitation of cable stayed structures [J].Journal of Sound and Vibration,1994,174(1):69-90.
[3]DAS R,PANDEY A D,SOUMYA,et al.Progressive collapse of a
cable stayed bridge [J].Procedia Engineering,2016,144:132-139.
[4]ZHOU Y F,CHEN S R.Numerical investigation of cable breakage
events on long-span cable-stayed bridges under stochastic traffic and wind[J].Engineering Structures,2015,105:299-315.
[5]WANG H,MAO J X,XU Z D.Investigation of dynamic properties
of a long-span cable-stayed bridge during typhoon events based on structural health monitoring[J].Journal of Wind Engineering and Industrial Aerodynamics,2020,201:104172.
[6]KIM B H,PARK T.Estimation of cable tension force using the
frequency-based system identification method [J].Journal of Sound and Vibration,2007,304(3/4/5):660-676.
[7]REN W X,HU W H.Cable modal parameter identification.Ⅰ :
theory [J].Journal of Engineering Mechanics,2009,135(1): 41-50.
[8]REN W X,HU W H.Cable modal parameter identification.Ⅱ :
modal tests[J].Journal of Engineering Mechanics,2009,135(1): 51-61.
[9]晏班夫,陳泽楚,朱子纲.基于非接触摄影测量的拉索索力测试[J].湖南大学学报(自然科学版),2015,42(11):105-110.YAN B F,CHEN Z C,ZHU Z G.Cable force identification based on non-contact photogrammetry system[J].Journal of Hunan Uni-versity(Natural Sciences),2015,42(11):105-110.(In Chinese)
[10]唐盛华,方志,杨索.考虑边界条件的频率法测索力实用公式[J].湖南大学学报(自然科学版),2012,39(8):7-13.
TANG S H,FANG Z,YANG S.Practical formula for the estima-tion of cable tension in frequency method considering the effects of boundary conditions[J].Journal of Hunan University(Natural Sci-ences),2012,39(8):7-13.(In Chinese)
[11]HUA X G,NI Y Q,CHEN Z Q,et al.Structural damage detection
of cable-stayed bridges using changes in cable forces and model updating[J].Journal of Structural Engineering,2009,135(9):1093-1106.
[12]LI S L,WEI S Y,BAO Y Q,et al.Condition assessment of cables
by pattern recognition of vehicle-induced cable tension ratio[J].Engineering Structures,2018,155:1-15.
[13]LI H,ZHANG F J,JIN Y Z.Real-time identification of time-
varying tension in stay cables by monitoring cable transversal ac-celeration[J].Structural Control and Health Monitoring,2014,21(7):1100-1117.
[14]XU Z D,WU Z S.Simulation of the effect of temperature variation
on damage detection in a long-span cable-stayed bridge[J].Struc-tural Health Monitoring,2007,6(3):177-189.
[15]SOHN H.Effects of environmental and operational variability on
structural health monitoring[J].Philosophical Transactions.Series A,Mathematical,Physical,and Engineering Sciences,2007,365(1851):539-560.
[16]YANG D H,YI T H,LI H N,et al.Monitoring and analysis of ther-
mal effect on tower displacement in cable-stayed bridge[J].Mea-surement,2018,115:249-257.
[17]LIU X L,HUANG Q,REN Y,et al.Extraction of cable forces due
to dead load in cable-stayed bridges under random vehicle loads[J].Journal of Southeast University(English Edition),2015,31(3):407-411.
[18]ZHOU H F,NI Y Q,KO J M.Eliminating temperature effect in
vibration-based structural damage detection[J].Journal of Engi-neering Mechanics,2011,137(12):785-796.
[19]CHEN C C,WU W H,LIU C Y.Effects of temperature variation
on cable forces of an extradosed bridge[C]//Proceedings of the6th European Workshop on Structural Health Monitoring.Dresden,Germany,2012.
[20]CHEN C C,WU W H,LIU C Y,et al.Damage detection of acable-stayed bridge based on the variation of stay cable forces eliminating environmental temperature effects [J].Smart Struc-tures and Systems,2016,17(6):859-880.
[21]CHEN C C,WU W H,LIU C Y,et al.Elimination of environmen-tal temperature effect from the variation of stay cable force based on simple temperature measurements [J].Smart Structures and Systems,2017,19(2):137-149.
[22]WU W H,CHEN C C,JHOU J W,et al.A rapidly convergent em-pirical mode decomposition method for analyzing the environmen-tal temperature effects on stay cable force [J].Computer-Aided Civil and Infrastructure Engineering,2018,33(8):672-690.
[23]CHEN C C,WU W H,LIU C Y,et al.Diagnosis of instant and
long-term damages in cable-stayed bridges based on the variation of cable forces[J].Structure and Infrastructure Engineering,2018,14(5):565-579.
[24]郭震山,陈艾荣.缆索支承桥梁模态阻尼特性及理論分析[J].同济大学学报(自然科学版),2005,33(1):1-5.
GUO Z S,CHEN A R.Characteristics and theoretical analysis of modal damping of cable-supported bridges[J].Journal of Tongji University(Natural Science),2005,33(1):1-5.(In Chinese)
[25]周海俊,丁炜,孙利民.拉索-阻尼器-弹簧系统的阻尼特性分析[J].工程力学,2014,31(1):79-84.
ZHOU H J,DING W,SUN L M.Damping of taut cable with a damper and spring[J].Engineering Mechanics,2014,31(1):79-84.(In Chinese)
[26]张笑华,任伟新,禹丹江.结构模态参数识别的随机子空间法[J].福州大学学报(自然科学版),2005,33(S1):46-49. ZHANG X H,REN W X,YU D J.Structural modal parameter identification appling stochastic subspace identification[J].Jour-nal of Fuzhou University(Natural Science Edition),2005,33(S1):46-49.(In Chinese)
[27]CHOPRA A K.结构动力学理论及其在地震工程中的应用[M].谢礼立,吕大刚,译.北京:高等教育出版社,2007.
CHOPRA A K.Dynamics of structures:theory and applications to earthquake engineering[M].Translated by XIE L L,L? D G.Bei-jing:Higher Education Press,2007.(In Chinese)
