“双减”背景下提高小学数学课堂教学质量的策略

李勤莉 褚夫建

2021年7月，中共中央办公厅、国务院办公厅印发《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》（以下简称“双减”），“双减”政策的颁布和落实，给数学教师的课堂教学带来了较大的挑战。“双减”要求提高课堂教学质量，因此教师要能够依据不同学段学生的实际情况来科学、规范地实施教学，要丰富教学内容的呈现形式，要利用多种教学资源提高学生的课堂兴趣。此外，教师还要不断探索并创新教学的内容、方法和形式，如组织实践探究类的活动、鼓励学生动手操作、融入数学游戏或故事等，以此来创新数学课程的内容，使学生对新知展开自主建构，提高学生“学”的积极性，让学生在课堂上“学足”“学好”“学饱”。为了进一步提高课堂教学质量，教师还需要在课堂上给学生更多“参与”“体验”“探究”的时间，从帮助他们巩固所学、发展综合能力的角度来优化课堂教学活动的设计，逐步提高数学“教”与“学”的整体效率和质量。

一、增加课堂趣味元素，激发学生学习兴趣

在“双减”背景下，如何提高数学课堂的整体效率成为很多教师关注的重点问题。要想促进效率的稳步提升，必然要想办法调动学生对数学课程的兴趣。“双减”背景下的数学教学内容不能“千篇一律”，教师要不断探索并创新课堂活动的形式，借助组织数学游戏、讲述数学故事等，增添数学课堂的趣味元素，提高学生“学数学”“用数学”的兴趣。

具备较浓的学科兴趣是让学生保持专注学习状态的一个关键因素。小学阶段的学生具有喜新、好玩的特点，他们对于一些新鲜、有趣的事物有着很强的好奇心。教师必须针对该阶段学生发展的总体特点来设计教学活动，可适当地融入一些数学游戏内容，向他们讲述一些数学故事等，以此来提高课堂教学的“趣”。这样，学生就会在数学课堂中产生愉悦的学习体验，进而对探索数学知识充满动力。

例如，在教学“最小公倍数”这部分内容时，我引入了《孙子算经》中的一道经典名题，由于著作是文言文，小学生难以读懂，所以我选择用白话的形式来引入：在《孙子算经》这本著作中有一道“物不知其数”的名题，题目是这样的，现在有一些物品我们不知道它们的数量，如果3个3个地去数，最后会剩余2个;如果5个5个地数，最后还会剩下3个;如果7个7个地数，最后还会剩下2个。你们知道这些物品究竟是多少个吗？

这样，学生的思维力、注意力和精力都被吸引过来，他们对这道题感到好奇。但是，按照学生的现有认知水平，这道题对他们来说有很大难度。所以，我又结合学生身边真实的情境，对该题进行了适当地改编：在体育课上老师组织大家站队，如果按每一列5个人站，最后还剩下2个人;如果按每一列7个人站，最后还剩下4个人;如果按照每一列13个人站，最后还剩下10个人。请你们算出这个班有多少人？

把数学文化中的名题演变成学生身边所熟悉的关于5、7、13的最小公倍数问题，就能够激发学生对“最小公倍数”的学习兴趣。

二、设计实践探究活动，锻炼学生学习能力

小学数学课有着很强的实践性，所以教师在实施教学时必须要与学生的生活实践进行联系，尽可能地给学生提供“参与”“体验”“实践”“探究”的空间和机会，让学生在“做中学”、在“实践中感知”。这样，一方面可以唤醒学生以往的经历或学习经验;另一方面，可以让学生参与到生活实践中，去体会数学知识的存在、运用。精心设计实践探究活动，既能帮助学生巩固所学知识，又能提高学生的数学技能，还能使学生的实践探究能力得到相应的发展。

“双减”背景下的数学教学，应该体现其“实践性”的特点，在课堂上，教师要摆脱那种单纯向学生“灌输”知识的现象，要注重给学生提供“过程探究” “参与实践”的空间和机会，使他们成为课堂的“小主人”。教师要让学生通过自己的思维和能力来发现、分析并解决问题，在此过程中提高综合能力，获得综合发展。教师还要转变那种“重知识传输、轻实践探究”的思想，要让学生在大量的实践活动中习得新知、获取更多能力，使他们学会多渠道、多层次地去探索问题，从而“学会”“学好”。

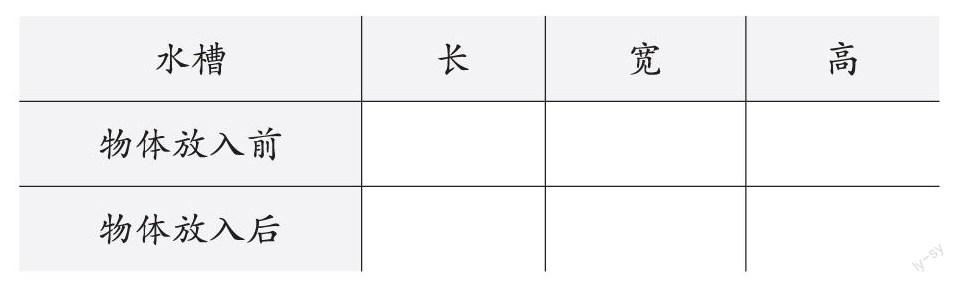
例如，在教学“不规则物体的体积”时，教师可以精心设计 “测量不规则物体的体积”的实践活动，要求学生通过实践探究来测量出某个物体的体积是多少，在此过程中发展他们解决问题、实践探究等综合能力。首先，教师可给每个小组提供一些具有不规则形状的水果，比如苹果、桃子、草莓等，再准备一个立方体的水槽。其次，教师要让学生在小组内运用恰当的方法来尝试计算，比如常见的“排水法”：把水果扔进水槽内，观察放进水槽之前和之后水的高度变化，观察、记录其中的数据，并完成下列表格。

最后，各组成员开始计算水果放入前水槽里原有水的体積及放入水槽之后水和水果的总体积，再将结果相减，从而计算出水果的体积。这样，就能够锻炼学生的动手能力，培养学生进行数学探究的意识。

三、把握课堂提问难度，培养学生数学思维

“渐进性”指的是课堂教学内容的难度不能采用“一刀切”的形式，在难度设置上要体现一定的“梯度”，要尽可能地把所教内容由易到难地向学生呈现，让学生的个体思维也从浅至深地逐渐发展。学生在学习的过程中，要有“渐入佳境”的体验，这不仅与小学阶段学生的发展特点相符，而且也有利于教师把握学生在学习能力方面的差异。所以，在实际教学中，教师要设计不同难易度的学习内容，帮助学生实现“减负增效”的数学学习效果。

要想在课堂提问中开发学生的个体思维，教师就需要根据学生在智力水平、学习方法、数学基础以及原有认知水平上的差异，采用“渐进性”的问题设计方式。教师在设计问题的过程中要考虑到各层次学生的可接受水平，将问题分成不同的梯度，让具有不同基础的学生都“有饭可吃”“有问可思”。通过“渐进性”的提问，可以解决学习能力较强的学生“吃不饱”、学习能力较弱的学生“消化不了”的问题，让学生的思维也由浅至深地获得发展，使学生凭借自己的思维能力来解决问题，促使其思维品质得到提升。

例如，在教学“小数的加法和减法”时，我向学生展示了买菜时的小票，并针对不同层次的学生提出了相应的问题。

【基础性问题】请问买五花肉花了多少钱？（考查学习能力较弱的学生小数的读法和写法，花了10.8元）

【巩固性问题】买西红柿和西兰花一共花了多少钱？（考查学习能力中等的学生小数的加法运算，7.3+5.8=13.1元）

【拓展性问题】请你根据这张小票设计一个关于减法的问题。如鸡蛋比鹌鹑蛋贵了多少钱？（考查学习能力较强学生的创造性思维）土豆比茄子便宜多少钱？

这样，学生的思维也是从浅至深地发展，如果他们学有余力，还可以向更高层次的問题去挑战，进一步开发数学思维。

四、组织学生动手操作，提高学习效率

“目的性”指的是现阶段教师所采取的教学策略必须与国家推行“双减”政策的目标相一致。作为数学教师，应该熟知“双减”的要求和学科育人目标，完善课堂教学的内容、方法以及形式。数学教学的目的之一是促进学生综合能力的形成和发展，所以只有针对学生发展的总体特点来设计教学策略，才能保证每一个“减负增效”的教学活动都朝着正确方向实施。

小学生对于周边的事物有着一定好奇心，他们好动、好玩，教师要针对学生发展的总体特征来优化教学活动的设计，要组织学生动手操作，让学生在“做中学”，在动手的过程中积累相应的操作经验。教师要在学生动手的过程中，调动学生的感官，引导他们用眼观察、用脑思考。这样，不仅可以促进学生对某个事物的深度思考，也能使他们的操作能力得到发展，还能提高学生对新知的接收速度和学习的整体效率。因此，要保证数学教学的高效，教师就要设计多样化的操作活动，培养学生的动手操作能力。

例如，在教学“认识长度单位”时，我先给学生抛出了一个难题：“大家在没有尺子、没有其他测量工具的情况下如何把课桌的长度测量出来呢？你有办法吗？”有的学生说：“老师，可以用手来测量呀，用拇指和中指之间的距离来量。”还有的学生说：“还可以用手臂量，比一比桌子有几个手臂那样长。”我针对学生的想法进行评价：古代人会把拇指和中指之间的距离称为“拃”，以此来测量某物的长度。然后，我引导学生自己量一量，通过这样的方式，降低学习难度，提高课堂教学效率。

五、设置分层课后作业，满足学习需求

“差异性”指的是学生在家庭环境、数学基础、学习方式、智力水平以及原有的认知水平等方面存在的差异，教师必须针对这种差异来实施相应的个性化作业设计。教师可以布置不同层次的课后作业，以此来满足不同水平学生的需求，让他们结合自己的能力来选择相应作业进行建构。在此过程中，可以让每个层次的学生都在原有能力基础上得到有针对性的发展。在“双减”政策的引领下，教师要秉持“差异性”的原则来安排教学、设计作业，保证各层次学生的能力水平都能得到提升。

在有些教师的数学课堂中，仍然存在“满堂灌”“一刀切”的现象，而在作业的设计中也存在布置“统一作业要求”“统一难度”“统一完成时间”的现象。这样就会忽略学生在智力水平、学习能力以及原有认知基础等方面的差异，不利于促进每个层次学生的共同发展。教师设计分层次的作业，能让学习能力较强的学生“吃得饱”，让学习能力较弱的学生“消化得掉”，满足各层次学生的个性需求，使每个学生在原有基础上都得到不同程度的发展，增加他们学习数学的信心。

例如，在学完“百分数”之后，我设计了如下一组课后作业。

【基础填空题】

1.请计算，7是14的   _________%，14是7的_________ %;

2.请计算，7比14少_________%，14比7多_________%;

3.找出单位“1”并列出算式，我们班男生有25人，女生有20人，请解答：

（1）男生人数是女生人数的百分之几？单位“1”是_________，算式是_________ ;

（2）男生人数比女生人数多百分之几？单位“1”是 _________，算式是_________ ;

（3）女生人数比男生人数少百分之几？单位“1”是_________，算式是 _________ ;

（4）说说对“男生人数比女生人数多百分之几”“女生人数比男生人数少百分之几”的理解。

【选做题】（供学有余力的学生做）

1.六年级三班男生人数是女生人数的1.25倍，男生人数比女生人数多了百分之几？女生人数比男生人数少百分之几？

2.五年级一班男生人数比女生人数多25%，那么女生人数比男生人数少百分之几？

学生可以根据自己的能力来完成相对应的作业内容，这样就能让处于不同能力水平的学生都能获得发展。

（责任编辑：杨强）