对角互补不要怕 双垂旋转巧转化

毛丽丽

对角之和是180°的四边形叫做对角互补四边形，通常被称为对角互补模型.作为图形与几何领域的典型图形，对角互补模型常常搭配哪些条件，常常和哪种图形同时出现，解题的常见策略又是什么呢？

一、典例解析

例 （2021·重庆B卷）如图1，在等边三角形ABC中，BD⊥AC，垂足为D，点E为AB边上一点，点F为射线BD上一点，连接EF. 将线段EF绕点E逆时针旋转60°得到线段EG，连接FG. 若E不与点A，B重合，GF的延长线交BC边于点H，连接EH，求证：BE + BH = [3]BF.

分析：本题除∠ABC和∠EFH互补外，还有一个“秘密武器”就是对角线BD平分∠ABC，充分利用角平分线的特性，借助作双垂线或旋转构造全等三角形即可解决问题.

解法1：如图2，过点F作FM⊥BA于M，FN⊥BC于N，

∴∠FME = ∠FNH = 90°，

∵BD⊥AC，∴BD平分∠ABC，∵∠ABC = 60°，

∴FM = FN，∠MFN = 120°，

∵∠EFH = 120°，∴∠MFE = ∠NFH，∴△FME ≌ △FNH，

∴ME = NH，∴BE + BH = BM - ME + BN + NH = BM + BN.

在△FBM和△FBN中，∠FMB = ∠FNB = 90°，FB = FB，∠FBM = ∠FBN = [12]∠ABC = 30°，∴△FBM ≌ △FBN，

∴BM = BN = BF·cos30° = [32]BF，∴BE + BH = [3]BF.

解法2：如图3，以点F为中心，将FB逆时针旋转120°交BC于P，

∴∠BFP = ∠EFH = 120°，∴∠EFB = ∠HFP，

∵BD⊥AC，∴BD平分∠ABC，∵∠ABC = 60°，∴∠FBP = 30°，∴∠FPB = ∠FBP = 30°，

∴FB = FP，∴△FEB ≌ △FHP，∴BE = PH，∴BE + BH = PH + BH = BP.

在△FBP中，过点F作FR⊥BC于R，∴BR = PR，

∵BR = BF·cos 30° = [32]BF，∴BE + BH = [3]BF.

点评：此题中，对角互补四边形外加一对角线平分其中一角形成全等型对角互补模型. 对角互补模型通常还会和等边三角形、等腰直角三角形、正方形等特殊图形结合起来考查，解题方法主要有过顶点作双垂线和旋转法.

二、模型策略

1.全等型对角互补模型，以双90°的对角互补模型为例.

（1）如图4，∠AOB = ∠DCE = 90°，OC平分∠AOB.

思路1：如图5，过点C作CM⊥OA于M，CN⊥OB于N，则△CMD ≌ △CNE.

思路2：如图6，以点C为中心，将CO逆时针旋转90°交OB于F，则△COD ≌ △CFE.

由此可得以下结论：①∠CDO + ∠CEO = 180°;②CD = CE;③OE + OD = [2]OC;④S△OCD + S△OCE =  [12]OC2.

（2）如图7，∠AOB = ∠DCE = 90°，OC平分∠AOB，∠DCE的一边与OA的反向延长线交于点D.

思路1：如图8，过点C作CM⊥OA于M，CN⊥OB于N，则△CMD ≌ △CNE.

思路2：如图9，以点C为中心，将CO逆时针旋转90°交OB于F，则△COD ≌ △CFE.

由此可得以下结论：①∠CDO = ∠CEO;②CD = CE;③OE - OD = [2]OC;④S△OCE - S△OCD =  [12]OC2.

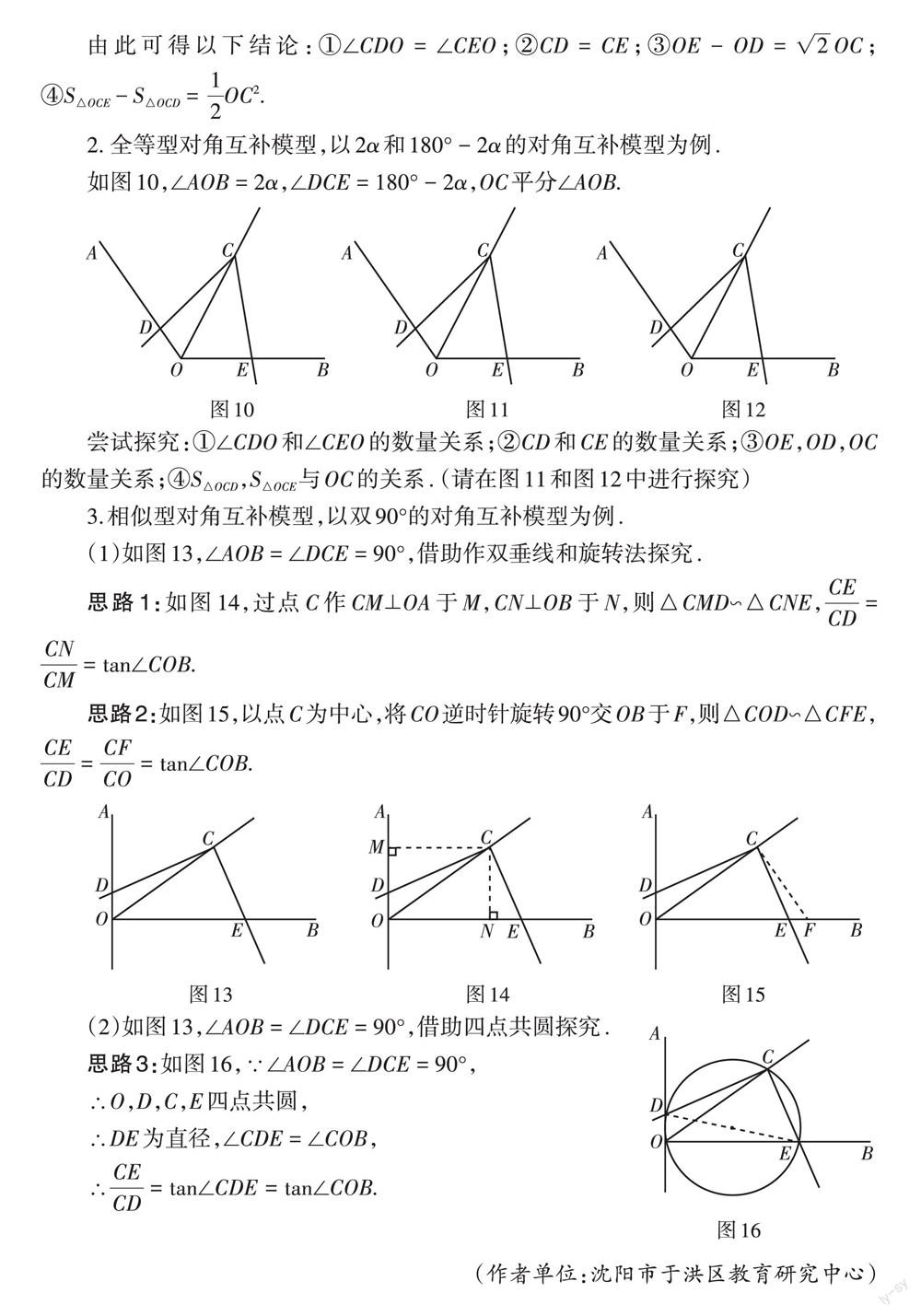
2. 全等型对角互补模型，以2α和180° - 2α的对角互补模型为例.

如图10，∠AOB = 2α，∠DCE = 180° - 2α，OC平分∠AOB.

尝试探究：①∠CDO和∠CEO的数量关系;②CD和CE的数量关系;③OE，OD，OC的数量关系;④S△OCD，S△OCE與OC的关系. （请在图11和图12中进行探究）

3.相似型对角互补模型，以双90°的对角互补模型为例.

（1）如图13，∠AOB = ∠DCE = 90°，借助作双垂线和旋转法探究.

思路1：如图14，过点C作CM⊥OA于M，CN⊥OB于N，则△CMD∽△CNE，[CECD=CNCM=tan∠COB].

思路2：如图15，以点C为中心，将CO逆时针旋转90°交OB于F，则△COD∽△CFE，[CECD=CFCO=tan∠COB].

（2）如图13，∠AOB = ∠DCE = 90°，借助四点共圆探究.

思路3：如图16，∵∠AOB = ∠DCE = 90°，

∴O，D，C，E四点共圆，

∴DE为直径，∠CDE = ∠COB，

∴[CECD=tan∠CDE=tan∠COB].

（作者单位：沈阳市于洪区教育研究中心）