任务驱动教学模式的实践研究
2022-05-30李玉兰胡启胜
李玉兰 胡启胜
任务驱动教学法是以生为本,以学习任务为主线,通过任务引领、问题驱动将学生引向深度学习的一种教学方法。笔者以九年级数学复习课“图形的旋转”为例,阐述任务驱动教学法在数学复习课教学中的运用。
一、确定指向核心素养的目标
任务驱动法在具体实施的过程中要首先确定好教学目标。本节复习课的教学目标如下:通过动画演示,巩固旋转及其性质;通过实例观察,引导学生归纳共点旋转图形的基本规律;通過特例探究,引导学生运用旋转及其性质解决复杂几何图形变换问题;组织学生经历图形观察、分析与比较的实践活动,积累用运动的观点认识图形的数学活动经验,会用数学的眼光观察图形共性、用数学的思维分析图形差异、用数学的语言表达图形规律。
二、设计合理的任务呈现
任务呈现指教学任务的设计,即教师将教学目标、知识点及重难点通过任务设计呈现出来。这是该教学法的核心内容,关系着一节课的成败。
本节课,学生已经学习了平移、轴对称、旋转三种变换,积累了一定的图形变换活动经验,但是在复杂图形中难以辨识旋转三要素,难以辨析旋转前后的图形关系,无法将旋转及其性质与基本模型联系起来。这说明旋转变换相关知识相对孤立地存在于学生脑海中,导致学生无法灵活运用其解决问题。
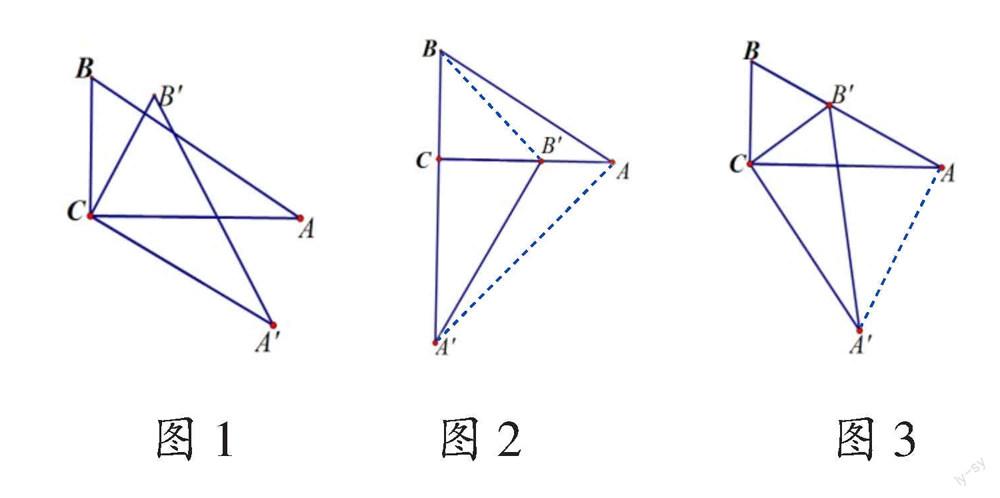
为了让学生根据旋转性质抓住变化中的不变量,发现几何模型是解决旋转问题的关键。笔者设置了三个学习任务。任务一:几何画板演示,将△ABC绕点C顺时针旋转任意角度得到△A'B'C(如图1),让学生从特例变换中观察三角形变换的过程,复习旋转的定义、性质。任务二:几何画板演示,分别将△ABC旋转得到图2、图3,让学生观察△ABC位置变化的过程,分组探究对应线段、旋转角和三角形之间的关系,归纳、总结共点旋转的基本规律。任务三:类比观察△ABC旋转后的不同位置,运用共顶点旋转规律计算新线段(虚线)的长。
在任务一中,通过几何画板动画演示,学生重温了旋转及其性质等基本知识,完善了旋转的知识网络,感悟到数学表达的准确性和严谨性。任务二和任务三引导学生重温图形全等、相似的性质,归纳图形旋转过程中“变”与“不变”的规律,如“共点等距,旋转全等”,从全等和不变性两个角度对旋转法进行探索学习,认识到共点旋转模型的本质,帮助学生积累用运动的观点认识图形的数学活动经验。
三、保障任务实施的有效策略
教师在课堂上要充分创设教学情境,运用多种策略促进任务的完成,如依问导学、合作探究、精讲点拨、设置评价等策略。
1.依问导学,以问促学
教师要设计富有启发性的问题,注重用多种方法引导学生自主学习,发展学生的创造性思维。以任务一“复习旋转的定义、性质”为例,笔者设计了“用几何语言描述这个变换”“在这个变换过程中,边、角没有发生变化的是哪些?△ABC的大小和形状是否发生了变化?”“结合△ABC旋转过程填空”3个子任务。层层深入的任务设置,从几何语言的表述到图形关系的观察,再到旋转共性的归纳,帮助学生调动原有知识、经验,深入讨论问题,推动了问题的解决。学生通过完成任务,自然而然地明确了旋转及其性质,进一步构建并完善了旋转知识体系。
2.合作探究,优化思维
教师要善用小组比赛有效激发学生参与课堂探究的积极性。基于三大任务的复杂性和综合性,笔者针对每个大任务分别设计了不同的子任务,将其适度分解成一系列学习活动,为学生顺利完成大任务搭建台阶。以任务二“总结共点旋转的基本规律”为例,笔者设计了3个子任务:①Rt△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转90°得到△A'B'C,图中有哪些全等三角形?相似三角形?特殊三角形?②将△ABC绕点C顺时针旋转得到△A'B'C,点B的对应点B'刚好落在线段AB上,图中有哪些全等三角形?相似三角形?特殊三角形?③Rt△ABC旋转到图2、图3后,图中的全等三角形之间有什么共同位置特征?相似三角形之间呢?共顶点的旋转一般会有哪些基本结论?
在任务一的交流讨论中,师生共同回顾了旋转及其性质等基本知识,同时也对旋转知识进行了系统梳理。此时,教师要及时引导学生探究任务二,利用旋转的等距性、等角性、全等性,发现全等是因,相似是果,引导学生合作探究,归纳、总结出“共点等距,旋转全等”,“共点等角,旋转相似”的“共点旋转”本质特征。整体观之,旋转、全等和相似层层递进,环环相扣,彰显综合性,有利于学生重构旋转知识体系。
3.精讲点拨,拓展提升
此环节,笔者根据学生任务完成情况及小组合作探究中发现的问题,重点讲解重难点、易错点,帮助学生解惑答疑,总结规律。同时,笔者结合教学需要,提出更高层次的学习任务,提升学生对知识的掌握程度。
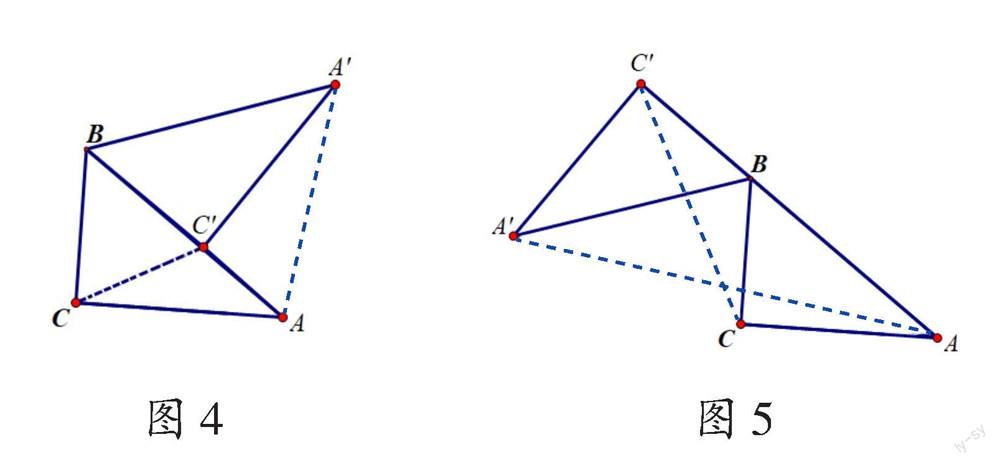
针对研究共点旋转变换的任务三,笔者设计了“画一画”“求一求”“说一说”3个子任务:“在△ABC中,∠BCA=90°,BC=6,AC=8,将△ABC绕点B顺时针旋转得到△A'BC',点C'、A、B三点共线。①你能画出旋转后的图形吗?②求线段CC'的长度。③你认为共点旋转变换需要理清哪些关键要素?”
教师先引导学生运用旋转的性质画出旋转后的图形(如图4、图5),再引导学生不断尝试改变△A'BC'的位置,感悟在图形变换过程中图形要素间的位置关系和数量关系,提升学生识别几何语言的能力,帮助学生发现蕴含的不变关系——点C'到点B的距离保持不变。
学生通过画图、分析、操作、实践、应用等活动在具体问题中把握“共点等距即全等,共点等角即相似”的共点旋转特征,加深了对旋转定义、性质的理解。
4.适时适度,设置评价
评价可以让教师了解教学目标实现的程度及学情,从而反思教学设计,同时还可以激励、调动师生在教学过程中的积极性。
一是分层达标检测。学生在完成任务后,教师要引导学生完成相应的达标训练。达标训练任务清单上的题目设置要有梯度,学生要独立完成。学生完成习题后,教师要公布答案,组织小组成员交换批改。教师可以随机抽取若干个学习小组的答题情况,及时掌握学生的学习效果,针对薄弱点实施强化措施的同时,为下一节课的目标设定寻找依据。二是自我矫正。借助学生自评、小组互评、教师评价结果,学生能了解自己对当堂所学新知的掌握程度,进一步查漏补缺,完善知识建构,不断积累反思学习的思维方法,进一步提升自主学习能力。
(作者单位:李玉兰,襄阳市第十中学;胡启胜,襄阳市襄城区教育科学研究中心)
(本文系2021年湖北省基础教育优秀教学改革实验项目、湖北省教育规划2021年度重点课题“区域任务驱动式教学模式构建的研究”的研究成果。课题编号:2021JA149)
责任编辑 孙爱蓉
