氧化钕中杂质氧化镍含量的测定及测量结果的不确定度分析

朱小龙

(宁波市计量测试研究院，浙江 宁波 315048)

烧结钕铁硼是目前世界上磁性最强的稀土永磁材料，作为稀土元素之一的钕是其中的主要成分之一。稀土矿产是我国重要的战略资源，原材料的成分配方不仅决定了其成本，也决定了最终钕铁硼产品的各项性能，因此保证原料纯度、检测其杂质含量显得尤为重要。电感耦合等离子体发射光谱法(ICP-OES)是一种常见的检测方法(杨平等，2020)，但传统化学检测实验室在报告中一般只给出样品的检测结果，很少给出其结果的不确定度大小，而中国合格评定国家认可委员会(CNAS)能力认可准则明确要求化学检测领域相关人员需对结果进行不确定度评定(中国合格评定国家认可委员会，2021)。近年来，叶晓明(2012)研究了可靠性评价的各种流派和方法，翟洪稳等(2021)总结了不确定度评定在食品领域的应用，雷晶等(2020)分析了环境监测分析方法标准中4种元素的不确定度分析及应用，更有专业人员以各自涉及的不同仪器和不同检测方法对具体项目进行了不确定度的分析和评定(康菁等，2020；唐平等，2021；张丽萍等，2021；刘芳美等，2021；李津等，2021)，臧慕文等(2012)详细研究了成分分析中的数理统计及不确定度评定。另外，国家有关部门也出台了测量不确定度评定与表示的相关规范(叶德培等，2013)。本文以稀土氧化物氧化钕中氧化镍含量的检测为例，首先用ICP-OES法进行相关检测获得含量结果，其次对整个过程中的影响因素进行相对不确定度分量计量，最终合成相对扩展不确定度，希望对稀土检测行业的发展提供理论参考。

1 方法原理

氧化钕作为重要的稀土原材料，其纯度决定了其价值。实验室普遍依据GB/T 12690.5《稀土金属及其氧化物中非稀土杂质化学分析方法 第5部分：钴、锰、铅、镍、铜、锌、铝、铬、镁、镉、钒、铁量的测定》、采用ICP-OES法测定氧化钕中杂质含量，以高纯氧化钕为基体配制系列标准溶液，以基体匹配法校正基体对测定的影响，试样以硝酸溶解，在稀硝酸介质中，直接以氩等离子体光源激发进行光谱测定，最终测得氧化钕中氧化镍杂质的含量，并通过计算各影响因素的不确定度分量，合成最终相对扩展不确定度。

2 检测方法

2.1 试剂和仪器

试剂有超纯水(一级水，电阻率18.2 MΩ·cm，25℃)、氩气(林德气体，纯度>99.999%)、硝酸(国药集团，优级纯)、高纯氧化钕(江阴加华，99.999%)和镍标准溶液(钢铁研究总院，1 000 mg/L)，仪器有容量瓶(申玻)、移液枪(赛默飞)、ME104电子天平(梅特勒托利多)、ULTIMA2电感耦合等离子体发射光谱仪(日本HORIBA)。

2.2 仪器工作条件

电感耦合等离子发射光谱仪工作功率为1 000 W，雾化气流量0.90 L/min，等离子气流量12.4 L/min，护套气流量0.2 L/min，护套气压强0.28 MPa，辅助气流量0 L/min，元素镍(Ni)的分析波长232.504 nm。

2.3 试料

将99.999%的高纯氧化钕于950℃灼烧1 h，置于干燥器中，冷却至室温。称取10.000 0 g样品，精确至0.000 1 g，置于500 mL烧杯中，加50 mL硝酸(1+1)，低温加热至溶解完全，冷却至室温，移入100 mL容量瓶中用水稀释至刻度并混匀，制得100 mg/mL的氧化钕基体溶液。

将氧化钕试样于105℃烘干1 h，置于干燥器中，冷却至室温，立即称取1.0 g氧化钕试样，精确至0.000 1 g。用10 mL硝酸(1+1)低温加热至溶解完全，冷却后，用水定容至100 mL并混匀，制得氧化钕待测样品消解液。

2.4 标准溶液的配制

将氧化钕基体溶液和镍标准溶液按表1分别移入6个100 mL容量瓶中，并加入10 mL硝酸(1+1)，以水稀释至刻度并混匀，制得6瓶标准溶液。

表1 标准溶液配制表 c/(μg·mL-1)Table 1 The preparation of standard solution

依次进样6瓶标准溶液，仪器自动拟合一条以信号响应强度为纵坐标、标准溶液镍含量为横坐标的标准工作曲线。

3 测量结果及其不确定度分析

将1 g待测氧化钕样品的消解液进行光谱分析，根据标准工作曲线上的信号强度(I)可得溶液中的镍含量(c)，通过换算可得样品中氧化镍的质量分数(w)为0.002 7%。测量结果的不确定度分析与评价如下。

3.1 测量模型

氧化钕试样中杂质氧化镍含量的质量分数按下式计算：

w=10-6cV/km×100%

(1)

式中，w为氧化镍质量分数(%)，c为试样消解液浓度(μg/mL)，m为试样质量(g)，V为试样定容体积(mL)，k为单质与氧化物换算系数(0.785 8)。

3.2 不确定度来源

通过分析检测过程，其结果的测量不确定度来自测量结果重复性的相对不确定度、标准溶液配制过程中产生的相对不确定度、标准曲线拟合产生的相对不确定度、定容时产生的相对不确定度、试样称量时产生的相对不确定度和单质与氧化物换算系数k引入的相对不确定度这6个方面。

3.3 测量结果重复性的相对不确定度urel(w)

由电感耦合等离子体发射光谱仪重复测量10次待测样品的消解液，氧化镍含量的测试结果为0.002 69%、0.002 72%、0.002 74%、0.002 68%、0.002 73%、0.002 67%、0.002 72%、0.002 71%、0.002 70%、0.002 69%，平均值为0.002 7%，10次测量的标准偏差(S)为2.27×10-7。

实际测量时，在重复性条件下连续测量3次，以该3次测量算术平均值为测量结果，n=3，其相对不确定度为：

3.4 标准溶液配制过程中的相对不确定度urel(c1)

3.4.1 标准溶液的相对不确定度urel(c11)

标准溶液的相对不确定度是电感耦合等离子体发射光谱仪的误差来源之一，直接影响测量结果的准确度。标准溶液的不确定度通常由标准溶液证书给出，钢铁研究总院标准溶液证书上给出的标准值为1 000 μg/mL，扩展不确定度为U=4 μg /mL，包含因子k=2，所以其相对不确定度为：

urel(c11)=4/(2×1 000)×100%=0.2%

(3)

3.4.2 标准储备液配制的相对不确定度urel(c12)

使用1 mL的移液枪(V=0.002 mL，k=2)移取1.0 mL的标准溶液于100 mL的容量瓶(V=0.04 mL，k=2)中，用超纯水定容至刻度，得到10 μg /mL的标准溶液，其相对不确定度为：

×100%=0.102%

(4)

3.4.3 标准工作溶液稀释配制的相对不确定度urel(c13)

使用5 mL的移液枪(V=0.017 mL，k=2)分别移取1.0、2.0、5.0、10和15 mL的10 μg /mL的标准溶液于100 mL的容量瓶(V=0.04 mL，k=2)中，配合基体溶液，用超纯水定容至刻度，得到浓度为0.1、0.2、0.5、1.0和1.5 μg /mL的标准溶液，其相对不确定度分别为：

urel(0.1 μg/mL)={[0.017/(2×1.0)]2+[0.04/(2×100)]2}0.5×100%=0.85%
urel(0.2 μg/mL)={[0.017/(2×2.0)]2+[0.04/(2×100)]2}0.5×100%=0.43%
urel(0.5 μg/mL)={[0.017/(2×5.0)]2+[0.04/(2×100)]2}0.5×100%=0.17%
urel(1.0 μg/mL)={[2×[0.017/(2×5.0)]2+[0.04/(2×100)]2}0.5×100%=0.24%
urel(1.5 μg/mL)={[3×[0.017/(2×5.0)]2+[0.04/(2×100)]2}0.5×100%=0.30%

(5)

通过计算可知相对不确定度较大的为0.1 μg/mL的标准溶液，取其值urel(c13)为0.85%。

3.4.4 标准溶液配制过程中的相对不确定度urel(c1)

标准溶液配制过程中引入的相对不确定度为：

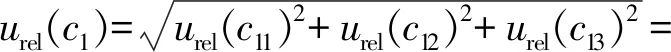
(6)

3.5 标准曲线拟合的相对不确定度urel(c2)

以6瓶系列标准溶液依次进样，每瓶溶液取3次有效数据，测定得到相应光谱强度，结果如表2所示。

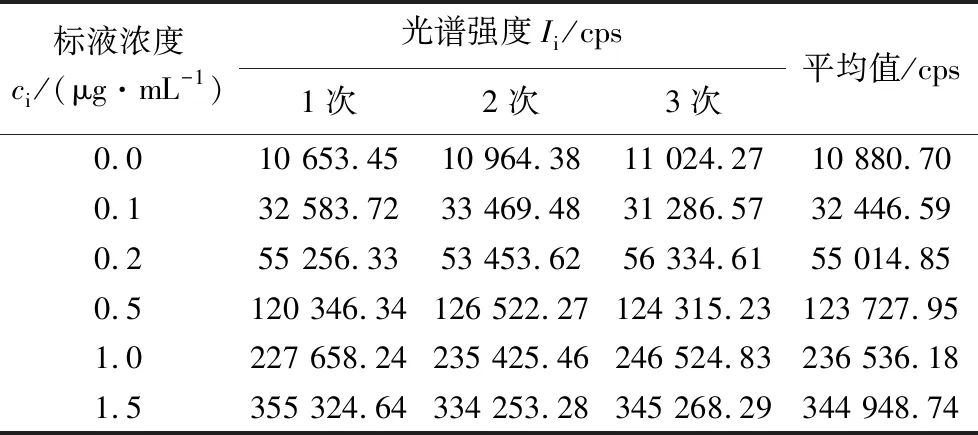
表2 标准溶液浓度与光谱强度Table 2 Concentration of standard solution and its spectral intensity

根据以上数据，以最小二乘法拟合直线方程：I=223 697.77c+108 92.06，得到a=108 92.06，b=223 697.77，R2=0.999 91 。由标准溶液线性拟合引入的相对不确定度计算如下：

/c×100%

(7)

(8)

把前面的相应数据代入公式计算可得：SR=5 317.29，urel(c2)=5.639%。

3.6 定容时产生的相对不确定度urel(V)

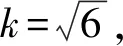
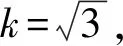
所以定容时产生的相对不确定度为：

3.7 试样称量时的相对不确定度urel(m)

用万分之一的电子天平称量样品，称样量为1.0 g，天平的检定不确定度为0.2 mg，变动性小于0.2 mg，包含因子k=2，所以：

≈0.022%

(12)

3.8 单质与氧化物换算系数k引入的相对不确定度urel(k)

镍的相对原子质量为58.693 4(2)，氧的相对原子质量为15.999 4(3)。

换算系数k引入的相对不确定度urel(k)很小，可忽略不计。

3.9 确定度的合成

综合以上所有不确定度的影响因素，各影响分量结果分别为：测量结果重复性的相对不确定度urel(w)=0.485%，标准溶液配制过程中的相对不确定度urel(c1)=0.879%，标准曲线拟合的相对不确定度urel(c2)=5.639%，定容时的相对不确定度urel(V)=0.047%，试样称量时的相对不确定度urel(m)=0.022%，换算系数k的相对不确定度urel(k)忽略不计。

因此，氧化钕中氧化镍杂质含量的检测结果的相对合成不确定度为：

(15)

包含因子k取2，包含概率p=95%，所以最终的相对扩展不确定度：

Urel=kurel=12%

(16)

4 结论

本文采用ICP-OES法测定氧化钕中杂质氧化镍的含量，以基体匹配法测得氧化镍含量为0.002 7%，其测量结果的相对扩展不确定度为(Urel=12%，k=2)。通过分析整个检测过程中的影响因素，总结出6个相对不确定度分量，其中以标准曲线拟合时引入的相对不确定度分量最大urel(c2)=5.639%，其次为标准溶液配制过程中引入的相对不确定度分量urel(c1)=0.879%。各相对不确定度分量的计算，可以为稀土矿石原料检测领域结果的不确定度分析提供参考依据。因此，在实际操作中首先要根据待测样品浓度含量调整标准溶液浓度点，以降低工作曲线跨度来提高线性，同时增加检测次数，可减小标准曲线拟合的不确定度分量；其次要选择低浓度标准溶液以减少标准溶液配制时的稀释次数，以此减小标准溶液配制过程中的相对不确定度分量。