基于图像光影重构的缎纹影光织物明度预测方法

郑雯洁， 张爱丹,2

(1. 浙江理工大学 纺织科学与工程学院(国际丝绸学院)， 浙江 杭州 310018；2. 浙江理工大学 浙江省丝绸与时尚文化研究中心， 浙江 杭州 310018)

织物图像是将织物从立体形态转化为平面形态的一种手段。数字形式的平面图像具有直观的视觉效果，以及便于数理统计和分析等优势，已被广泛应用于提花织物纹样提取[1]、网孔织物图像分割[2]、织物图像疵点检测[3]等。影光组织是一种能表现经、纬纱线颜色相互转化过渡的系列变化织物组织，常用于单层结构、重组织结构和双层结构提花织物的设计[4-6]，对其呈色规律的预测研究可为提花织物显色效果的设计提供参考。

目前对机织物呈色规律预测模型的探讨，主要有建立在单一织物组织基础上的几何模型[7]，以及基于区域颜色数据提取的平均计算方法[8]等。前者一般不考虑织物纱线因织缩造成的形变，以及经纬纱线交织形成立体结构的光影特点。另外，在高经纬密设计条件下，几何模型中的背景空隙因素作用不明显，使得几何模型并不适用于高经纬密缎纹影光组织提花织物呈色效果的预测计算。而基于区域颜色数据提取的平均计算法，通过在PS图像处理软件中，对织物组织图直接进行吸色，再对吸取的颜色进行平均值计算得出织物色值，作为建立织物呈色模型或色卡的依据。这种方法虽然可以反映织物的混色特征，但因研究对象是织物组织图像而不是实物样品，并不能代表真实织物表面的颜色值。上述2种织物颜色预测方法，都忽略了经纬纱线上下沉浮交织构成的微观立体结构所产生的大量光影信息，以及柔性纱线因织缩而产生的形变特质。鉴于此，本文以织物样品的实物图像为研究对象，提出一种适用于缎纹影光组织织物的明度预测方法，为影光组织的设计提供参考。

1 织物图像光影重构原理

将三维立体织物转化为灰度模式的数字图像，从而利用构成图像的像素灰度值，反映无彩色织物表面的明度信息。这种明度信息是综合性的，易受到图片采集条件的干扰，因此需将图像按一定方式进行处理，尽可能降低人为因素或环境因素的影响，才能用于目标研究。织物色的主要构成因素为织物组织和纱线，据此将织物图像分离为3层，分别为表示织物表面经纬浮长的经纬纱线图形层、经纬纱线交织形成立体结构的阴影层和表示纱线原材料质感特征的材质层。

图像的分层处理主要是为了得到不同图形因素的相对面积，为实际纱线色的赋值提供范围，而不是将拍摄图像作为重构织物图像明度的直接来源，具体方法见图1所示。根据织物图像的重构明度值与织物样品实际测量明度值的拟合结果，确定织物明度预测公式的各项变量，用于织物明度预测回归模型的构建。

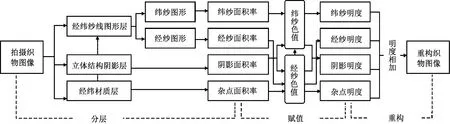
图1 织物图像光影重构研究方法示意图Fig.1 Diagram of light and shadow reconstruction method of fabric images

1.1 织物图像的分层提取

1.1.1 经纬纱线图形层

经纬纱线图形层是光影分离和重构的基础，主要呈现织物表面经纬纱线浮长的独立面积，以反映织物的组织结构、经纬密度与纱线线密度等特征。在织物图像中，阴影层和纱线材质层的重建都依附于这一层，同时也是反映织物纱线形变状态的重要图形层。

1.1.2 立体结构阴影层

阴影层由经纬纱线投影信息组成，随着织物组织和纱线规格的变化而不同。在织物图像中，阴影部分反映了经纬纱线上下起伏交织的立体状态，是区别于几何模型平面特性的关键因素。纱线阴影部分具有明暗渐变的特点，在提取过程中需要对其面积范围进一步确定。

1.1.3 经纬材质层

材质层反映了经纬纱原材料的图像特征，具体表现为类似杂点的纹理。杂点纹理提供了纱线材质本身的特性，如构成纱线的纤维及其成纱形式等方面的信息。根据经纬纱线的材质和颜色的变化，材质层对织物明度值的影响效果也不同。材质层为体现织物原材料特性预设了空间，为更准确预测织物色创造了条件。

1.2 分层图像的光影重构

光影重构是基于上述图像分层的二次筛选及重新组合，是指对各层图像数据的回归计算。图像的分层是为了更精确地反映原始织物图像的光影关系。

对于纱线图形层，由于织缩及纱线交织产生的扭曲形变，实际的织物经纬浮长面积不同于织物组织图理想状态下的面积。这一图层的提取决定了织物明度预测模型的基础数值。

对于阴影层，一方面经纬纱线上的阴影表现为灰度值渐变的像素点，因此需设定提取的临界值，以确定作为阴影的像素；另一方面当纱线为黑色或颜色较深时，投于之上的阴影通常难以察觉，因此阴影效应主要对白色或浅色纱线产生显著作用。

织物纱线颜色的深浅对材质层也有一定的影响。白色或浅色纱线在光源下即使产生亮点，对织物整体明度值并无太大影响。而在黑色或深色纱线上，这种亮点对视觉造成明显的干扰。此外，如织物纱线的纤维和成纱加工形式不同，产生的纹理图像也各不相同，需要区别对待。

2 织物图像分层与数据采集

2.1 织物样品织造与测色

以16枚3飞、5飞、7飞纬面缎纹为基础组织进行影光组织库设计，并进行织物样品织造。影光组织库在组织点过渡方向上，分别采用纬向加强和经向加强2种方法；每次增加的组织点数量等于基础组织循环数，共计6组各有15个组织的最小值影光组织库[9]。织物样品由1组白经和1组黑纬交织而成，其中经、纬纱组合分别为22.2、24.4 dtex×2的桑蚕丝，经纬密均为1 100根/(10 cm)。文中织物样品均由杭州宏创纺织有限公司生产织造。

对织物色卡样品进行背面拖裱，使其平整挺括，再采用美国X-rite爱色丽公司Color i7型台式分光测色仪进行测量。数据采集条件：颜色系统为CIEL*a*b*，观测角度为10°，测量孔径为25 mm，光源为脉冲氙灯D65。每块织物样品测试3次，取其明度平均值。

2.2 织物图像处理

2.2.1 织物图像采集与剪裁

采用欧美科台式数码电子显微镜(型号AO1017)进行织物样品图像采集，放大91.68倍，拍摄的织物图像长宽尺寸为2 592像素×1 944像素，如图2(a)所示。再将其统一导入MatLab软件中转换为灰度模式图像。

图2 织物图像分层提取及其图像例证Fig.2 Layered extraction of fabric images and its image illustration. (a)Original digital image; (b)Preprocess window image; (c)Connection area image; (d)Open operational image; (e)White warp image; (f)Black weft image; (g)Shadow image on the white warp; (h)Texture image on black weft

采用 imcrop 函数，按照同一起点和同一尺寸，将所有织物样品图像均裁剪为501像素×501像素的窗口图像，使其包含一个完整组织循环。计算各窗口图像的平均灰度值，将窗口图像中灰度值低于灰度均值的像素全部设为“0”，得到预处理的窗口图像，见图2(b)，之后的图像运算都基于该步骤图像的灰度信息。

2.2.2 开运算图像处理

开运算是一种对数字图像进行形态处理的方法，参与运算的对象有2个：目标图像和结构集合。本文实验的目标图像为预处理窗口图像，结构集合也称结构元素，其可以是任何形状，如线性、圆盘形等[10]。文中利用开运算方法主要是为了在消除预处理窗口织物图像中黑纬上杂点的同时，保留白经图形边缘的灰度像素点，为分离白经、黑纬图形提供最优图像方案。

在开运算处理中，结构元素的大小和形状设置是关键。文中结构元素的大小根据黑纬上杂点像素面积而定。先在MatLab软件中采用graythresh函数(Otsu算法)，对每幅预处理窗口图像进行阈值分割，得到连通域图像，见图2(c)。再将连通域面积降序排列，排除织物经、纬图形区域之后，得到最大杂点面积。以16枚3飞经向加强组织织物样品为例，分别在组织点连续增加到第5个和第11个时，相邻经纱上的经组织点产生连结，因此将1组影光组织织物分为 3 段提取。第1段中组织点连通区域数量最多，为16～20个之间；第2段数量为6个；第3段数量为1个。3段中需重点考察第1段第16个组织点连通区域之后的4个区域面积，若其中有1个区域与其他相差300像素以上即为最大杂点面积。根据上述方法得到每段最大杂点连通区域，再取其像素数量平均值，作为结构元素大小的根据。根据数据统计结果，文中最终采用半径为 5 像素的圆形结构元素进行开运算图像处理，经开运算处理的织物图像见图2(d)。

2.3 织物图像的分层提取与赋值

2.3.1 经纬图形区域的提取与赋值

灰度织物图像经开运算处理后，白经与黑纬区域被基本分离，见图2(d)。根据图像像素灰度值划分经、纬纱线图形，并计算所占面积率。先统计织物图像中灰度值为“0” 的像素数量，再计算其与图像总像素量的比值，即为黑纬面积比Sw1(%)；其余灰度值大于“0”的像素区域即为白经图形部分，其与图像总像素量的比值设为Sj1(%)。白经和黑纬的图形效果，见图2(e)和(f)。

在获得每个织物样品图像的经纬纱线的面积及其比值之后，再赋予各自实际的纱线色的色值。经测色得知，白色经纱的明度值(Lj)为 91.16，黑色纬纱的明度值(Lw)为 14.09。

2.3.2 白经投影区域的提取与赋值

图像开运算处理后，白经上的投影更加块状化，有利于灰度模式织物图像的像素提取。根据开运算后的图像灰度平均值，将大于平均值的像素部分赋值为“0”。此时图像中只保留了白经的深灰部分，见图2(g)。投影部分的像素数量与图像总像素数量的比值设为Sh1(%)。再从白经面积中减去白经投影面积，剩余部分的像素数量与图像总像素数量的比值设为Sj2(%)。白经阴影部分的明度值设为Lh1，取经纱和纬纱的实际明度值的中间值“50”。

2.3.3 黑纬杂点区域的提取与赋值

材质层杂点图像存在灰度变化，但仅有部分像素杂点对织物明度有所影响，因此需要设定杂点筛选临界值。将预处理窗口图像与开运算图像相减，得到杂点图像，见图2(h)。统计图像中灰度值为255的像素数量，即为黑纬杂点面积。这部分与图像总像素数量的比值设为Sh2(%)。再计算黑纬面积减去杂点面积，其差值与图像总像素数量的比值设为Sw2(%)。黑纬杂点部分的明度值设为Lh2，取白经实际明度值“91.16”。

3 实验结果与讨论

3.1 光影线性重构明度结果与分析

根据明度相加定律，织物明度为各部分明度之和，即为经纬纱线图形层、阴影层和材质层线性重构的还原过程。由上述3层图像的重构转化得到的织物综合明度计算公式如下：

Lzi=Sj2Lj+Sw2Lw+Sh1Lh1+Sh2Lh2

i=1,2,…,R-1

式中:Lzi为织物综合计算明度值；Sj2、Sw2分别为织物经、纬纱各自面积比；Lj、Lw为经、纬纱实测明度值；Sh1、Sh2分别为白经投影面积比和黑纬杂点面积比;Lh1、Lh2为阴影和杂点的明度值；R为织物组织循环数，文中取16；i为最小值影光组织库的取值范围，文中为1～15。

为考察各分层图对于织物明度的影响程度，分别计算织物样品图像的经纬纱线图形层、经纬纱线图形层结合阴影层，以及综合3层的织物明度值，再将3种计算结果与实物样品测色数据进行比较分析。文中以16枚7飞经向加强织物样品为例，其结果如图3所示。由图可知，由计算所得的织物经纬纱线图形层明度值(Lpi)大于实测明度值(L1)，但曲线走向与实测明度值一致，表明仅考虑经纬表面浮长无法较好地还原织物明度；增加白经阴影层计算所得的织物明度值(Lti)，更接近织物样品的测量明度，可见投影层对织物明度重构具有重要作用；再增加黑纬杂点层计算得到织物明度值(Lzi)，与(Lti)相比变化较小，从图中无法直接判断杂点层的改善作用。

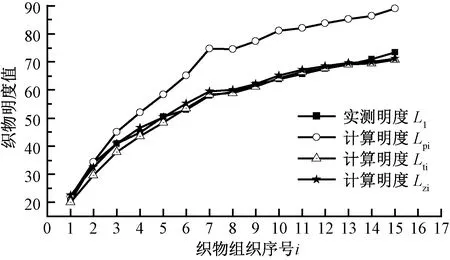
图3 织物明度曲线图Fig.3 Diagram of fabric lightness

下面进一步以3组飞数分别为3、5、7的 16 枚经向加强影光组织织物样品为分析对象，通过对3组织物样品图像的经纬图形层明度Lpi、经纬纱线图形层结合投影层的明度Lti，以及在前二者基础上增加材质层的明度Lzi分别与织物样品实际测量明度L1，进行单因素方差分析，结果见表1。表中：F值为上述3组计算明度值和1组测量明度值的组间方差和组内方差的比值，p值为各组均值相等的概率，作为计算明度数据与织物样品测量明度数据拟合度的评价值，F值越大且p值小于 0.05，表示数据拟合度越差，反之则拟合度越好。

表1 织物明度单因素方差分析表Tab.1 One-way analysis of variance for fabric lightness

从表1可见，增加纱线材质层后，3组织物的计算明度Lzi的p值均远大于 0.05，且F值相对其他2组更接近于0，发挥了进一步缩小计算值与实测值差距的作用。其中16枚3飞织物样品组的综合明度Lzi与实测明度的拟合度最佳，其次是16枚7飞、16枚5飞。

对3组织物样品的3种不同图像层组合明度值的拟合度分别取其均值，其中经纬图形层明度与实测明度的拟合度为0.15，增加阴影层后拟合度提高到0.76，再加入材质层后的明度拟合度上升为0.89，可见，基于织物图像分层图得到的线性光影重构明度，较好地还原织物实际明度，为文中明度预测模型的建立提供了变量选择的依据。

3.2 光影明度预测回归模型建立

根据上述线性光影重构获得织物明度的结果，文中以织物预测明度为因变量，以织物经纬图形、投影和杂点面积为自变量，建立二次多项式，以逼近实际函数表达关系[11]。其中织物经纬纱线图形面积与基于特定影光组织的织物样品的实际形变量(S)建立了联系，S由织物样品图像提取所得经纬纱线图形与其对应意匠经纬纱线图形二者面积的差值所得。此外，为便于运算，引入多个新变量以替换二次多项式中相应数量的由2个自变量乘积组成的单项式，即将二次多项式模型转为多元线性模型，见如下公式：

Y=B0+B1x1+B2x2+B3x3+B4x4+

B5x5+B6x6+B7x7+B8x8+B9x9

下面分别对 3 组经向、3 组纬向加强织物图像数据，以及将前二者全部组合在一起，形成包含经纬两向加强的6组织物图像数据，建立3个逐步回归分析预测模型。图像数据样本具体为从每组15个样本中随机选取13个作为训练样本，剩余2项为检验样本。将所有训练数据样本输入逐步回归分析模型，结果见表 2。

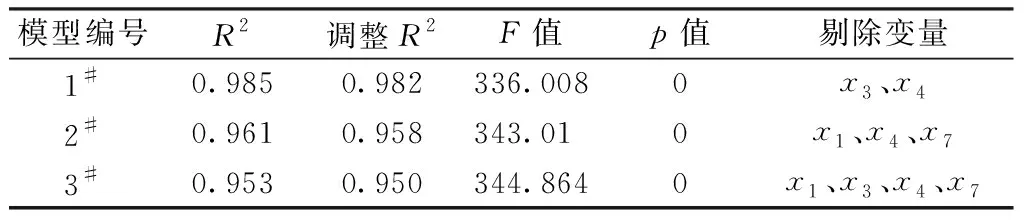
表2 逐步回归分析结果Tab.2 Results of stepwise regression analysis

注：模型1#基于3组经向加强织物的图像数据；模型2#基于3组纬向加强织物的图像数据；模型3#基于经、纬组合6组织物的图像数据。

表2中R2为自变量和因变量之间线性拟合度的检验值[12]，当R2越接近于1，表明数据和模型的拟合度越好。其中模型1和模型2的R2分别为0.982和0.958，且p值均小于0.01，说明模型与数据的拟合度较好。此外，模型1、2的数据拟合程度优于模型3，说明经、纬两向加强织物图像数据各自分别建立模型，有利于提高模型对明度预测的准确性。

最后根据逐步回归分析结果，去除对模型无明显影响的变量，分别得到经向加强织物和纬向加强织物明度线性回归模型，再将其还原为非线性回归模型：

Yj=-3.73+7.43x1+326.86x2+16.64x1x3-

Yw=30.13+240.27x2-1 712.78x3+510.75x1x3-

式中：Yj为经向加强织物的预测明度;Yw为纬向加强织物的预测明度。再用剩余的12项检验样本，分别对经、纬两向加强织物明度预测模型进行验证，结果见表3。表中样品4、7和9的预测明度值比实际测量值高，其余检验样品则比实际测量值低，验证结果表明，纬向加强织物预测模型的平均误差率为1%，经向加强织物预测模型的平均误差率为2%，总体相对误差在±4%以内，预测准确度较好，可用于影光效果织物的设计应用提供参考。

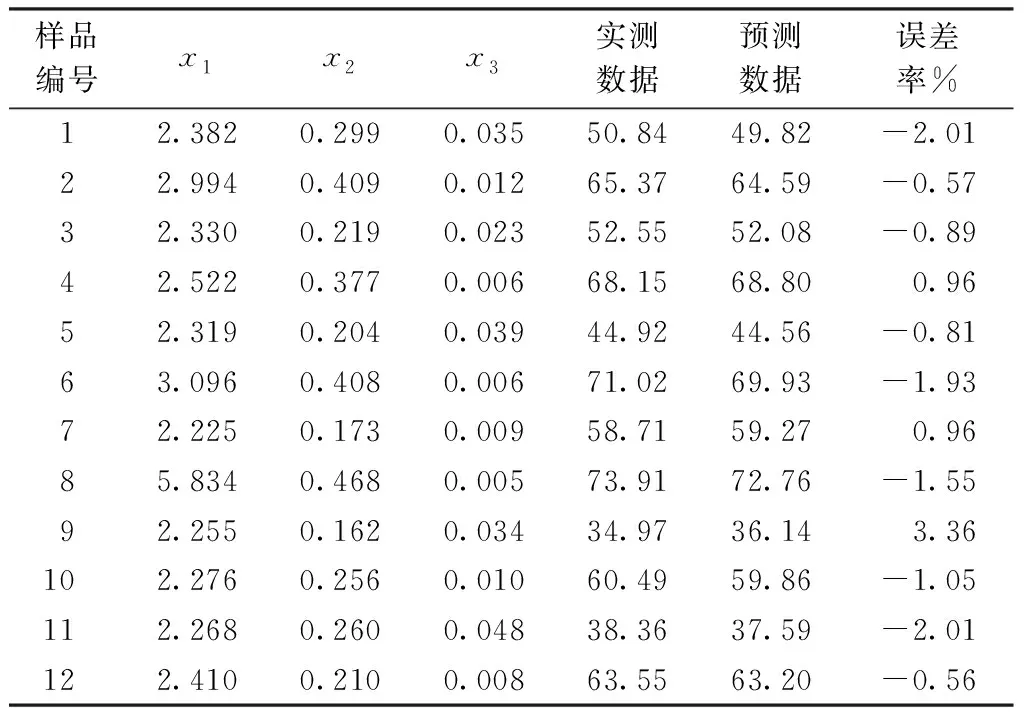
表3 预测模型验证结果Tab.3 Results of prediction model validation

4 结束语

本文基于织物实物图像的分层处理与光影重构，建立了适用于预测黑白缎纹影光组织织物明度的数学模型。为使明度预测模型具备较全面反映织物组织本身变化、纱线形变、纱线交织产生的立体光影效应，以及纱线材质等影响织物明度的因素，提出先将织物样品图像分为经纬纱线图形层、阴影层和材质层，以获取相关图形、图像的面积率，为替换实际经纬纱线颜色值提供区域范围，在此基础上建立织物明度计算公式。通过应用该计算公式对经分层的6组影光组织织物样品图像进行织物明度值的重构实验，并以织物样品实际测色数据为参照比较分析3种图像层的贡献度，为织物明度预测模型提供变量选择依据。

以经纬图形面积率、阴影面积率、杂点面积率为自变量建立二次多项式，基于78个实验样本数据进行逐步回归分析，并以此建立经向加强和纬向加强织物的明度回归预测模型。经过12项测试样本验证，该预测模型总体误差率在±4%以内，可较好地还原缎纹影光组织织物的实际明度，具有一定适用性，可为黑白影光效果织物的设计提供明度预测，并为构建彩色影光组织织物的颜色预测模型提供方法参考。

FZXB