以欠采样速率实现盲谱感知及二维DOA 估计

张 展，魏 平，高 林，张花国

(电子科技大学信息与通信工程学院 成都 611731)

无线电频谱资源匮乏，引入角度信息可以增加频谱利用率[1]，这使得频谱感知问题变为二维联合谱(空间谱与频谱)的感知问题。然而，以奈奎斯特率进行宽频谱感知会带来较大的数据处理压力。利用欠采样技术可以有效地降低采样率，实现以低速率进行盲谱感知与波达方向(direction of arrival,DOA)估计。

基于欠采样技术的谱感知与DOA 估计算法主要分为两大类：基于多陪集采样器的算法[2-6]和基于调制宽带转换器(modulated wideband coverter, MWC)的算法[7-9]。然而，上述算法解决的都是盲谱感知与一维DOA 估计的问题。文献[10]在文献[8]所提的L 形阵列的基础上，提出了一个三维阵列。该阵列能拆分为两个L 形阵列，并根据文献[8]所提出的算法，提出了一种基于ESPRIT 技术的算法，实现以欠采样速率进行频率与二维DOA 的联合估计。随后，文献[11]在文献[4]所提算法的基础上，在混合了多陪集与MWC结构的L 形阵列上，提出了一种能在欠采样速率下进行频率与二维DOA 联合估计的算法。然而，目前这样的算法有着复杂的硬件结构，且在低信噪比下性能受限。

本文提出了一种基于单通道MWC 的任意二维阵列的欠采样接收机结构，基于该结构提出了两种新的算法。这两种算法能充分利用MWC 采样器的特性[3]，在欠采样条件下实现盲谱感知与二维DOA 估计。提出的接收机结构与算法能大幅度降低硬件资源的消耗以及复杂程度，并在低信噪比环境下，仍能保持较好的感知性能。

1 背 景

2 欠采样阵列接收信号模型

2.1 单通道调制宽带转换器

MWC 结构的物理本质为：当接收信号um(t)在时域与周期信号p(t)相乘时，接收信号的模拟频谱Um(f)会 以fp=1/Tp为间隔进行连续平移，且乘上对应的尺度因子。该尺度因子为周期信号的傅里叶级数系数。当通过低通滤波器后，会保留通带范围Fs内 的频谱。该频谱为 F 范围内以fp为间隔的子频带谱与对应的尺度因子相乘后组合叠加的结果。

2.2 欠采样接收机结构

图1 单通道的调制宽带转换器

2.3 欠采样的接收信号模型

3 盲谱感知及二维DOA 估计算法

3.1 基于张量秩一分解的盲感知算法

此时，已经实现了对信号源的盲谱感知及二维DOA 估计，将该方法命名为JSS-2DOA-CP 算法。

3.2 基于子空间分解的盲感知算法

4 仿真实验

第一个仿真实验验证所提采样接收机结构以及对应盲感知算法的有效性。该仿真设置了11 个50MHz 带宽的复信号源。为了满足文献[9]中分析的系统参数选择条件，二维阵列设置为包含M=9个天线的L 形阵列，即每个子阵列分别包含5 个阵元。信噪比SNR设置为 0 dB。图2 描述了原始信号频谱以及JSS-2DOA-CP 算法和JSS-2DOAMUSIC 算法重构的信号频谱，并给出了其中一个信号源的重构频谱放大图。图3 给出了信号源的三维参数的估计图，图中的3 个坐标轴分别代表方位角θ 、俯仰角α、载波频率f。

图2 原始信号频谱及重构的信号频谱

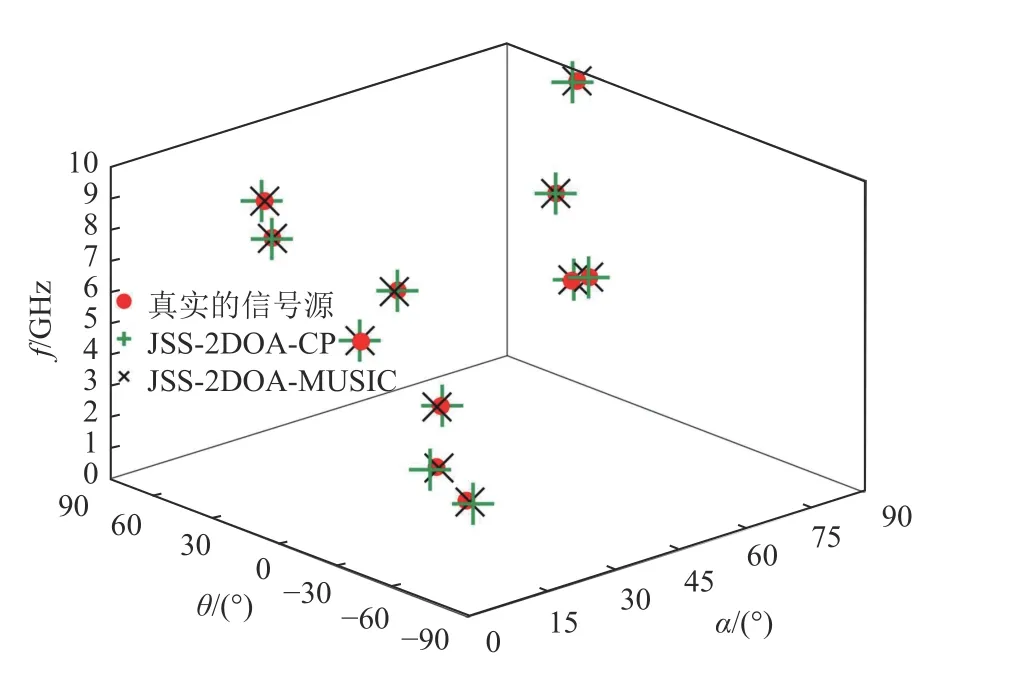
图3 信号三维参数估计图

从图2～3 中可以看出，当系统设置满足条件时，能够完成对信号源所在子带的正确估计，因而能够估计得到信号的子带频谱，并由此重构出完整的信号谱。信号子带频谱的正确估计以及所在子带位置的正确估计保证了载波频率的高精度估计，因而对信号源的方位角和俯仰角也能正确估计。此外，仿真环境对应的奈奎斯特采样率为1 0 GHz，而该系统用到了9 个天线，每个RF 电路的采样率为400 MHz，因此系统总采样率为3 .6 GHz，远低于奈奎斯特率。该仿真也说明了所提出的采样结构以及对应的算法能够保证用以远低于奈奎斯特率的总采样率，在噪声环境下，实现盲谱感知以及二维DOA 估计。

第二个实验是为了验证所提算法的性能，选择了文献[10]所提出的基于CaSCADE[8]的衍生算法和文献[11]所提出的基于PABSS[4]的衍生算法作为本仿真实验的对比算法。该仿真设置了两个带宽为50 MHz 的复信号源。所提的接收机结构是包含7个天线的L 形阵列，即M=7。为了保证公平性，即系统的总采样率一致，设文献[10]中算法对应的三维阵列，每个子阵列包含10 个天线，总计28 个天线；设文献[11]所提的L 阵列，每个子阵包含15 个天线，总计29 个天线。因此，本文所提的系统总采样率为2.8GHz，文献[10]和文献[11]算法的总采样率分别为2 .8 GHz 和2 .9 GHz。仿真的信噪比SNR 变化范围以3 dB 为间隔，设置为− 10 ～2 0 dB。图4～6 分别表示了估计的载波频率、俯仰角、方位角的RMSE 曲线。

图4 载波频率的估计性能

图5 俯仰角的估计性能

图6 方位角的估计性能

从图中可以看出，所提算法的性能相比于另外两种算法，在谱重构以及频率估计的性能上有着显著优势，这是因为本文算法的载波频率估计依赖于对信号源所处子频带位置的估计，因此频率的估计精度会大幅度提高，进而带来谱重构的优势。此外，方位角和俯仰角的估计性能在低信噪比情况下也有显著优势。不仅如此，相比于对比算法的系统设计，本文所提出的系统结构有更少的硬件资源开销，因此本文所提的接收机结构以及对应的盲感知算法，能在降低资源开销的同时仍保证感知性能的鲁棒性。

5 结 束 语

本文提出的基于压缩采样的盲谱感知及二维DOA 估计算法，充分利用了MWC 中的周期信号产生对应的傅里叶级数系数矩阵，通过估计出信号源频谱所处的子带位置，以此提高载波频率的估计性能，进而使得在低信噪比环境下，信号源的方位角和俯仰角的估计精度大幅度提高。这种区别于传统的利用空间相位信息估计载频与二维度DOA 的思路，大幅度提高了感知性能以及估计的鲁棒性。此外，设计的接收机系统以及对应的感知算法能有效降低系统硬件资源的开销，对认知无线电中多维联合谱感知问题具有重要意义。