精确Grover 量子搜索算法概述

李冠中，李绿周

(中山大学计算机学院 广州 510006)

求解无序数据库搜索问题的Grover 量子搜索算法[1]于1996 年被提出，相对于经典算法有平方级别的加速。自问世以来，得到广泛应用，如被用于求解最小值查找问题[2]、串匹配问题[3]、量子动态规划[4]及计算几何问题[5]。不仅如此，针对Grover算法本身的扩展也不少，如量子振幅放大[6]、图上量子游走搜索[7]、不动点量子搜索[8-9]及本文要介绍的精确Grover 量子搜索算法[6,10-11]。

1 原始Grover 算法及其缺陷

无序数据库搜索问题可以抽象地描述如下，在大小为N=2n的 无序数据库中，有M个元素是符合要求的，这些目标元素通过一个函数f:{0,1,···,N−1}→{0,1}来 标识：若编号为x的元素为目标元素，那么f(x)=1； 否则，f(x)=0。假设有一个可以识别搜索问题目标元素的黑盒：要判断编号为x的 元素是否为目标元素，只需要将编号x输入黑盒，它就会输出f(x)的值。现在希望以尽可能少的黑盒调用次数(称之为查询复杂性)，找出一个目标元素。

在量子计算中，实现函数f(x)的黑盒的作用效果是一个酉操作Of，其在计算基态上的作用效果为：

2 精确Grover 量子搜索算法

2.1 大步小步

2.2 共轭旋转

2.3 三维旋转

这一方法[11]的思路为：把G(ϕ,ϕ)在 正交基 |A〉和|B〉下的二维酉矩阵对应到相应Bloch 球中的三维旋转，再通过选取适当的角度 ϕ和旋转次数k，使得Gk(ϕ,ϕ)|ψ〉在 该Bloch 球面上与 |B〉重合。

具体来说，由于任意二维酉矩阵都可以写成下式右边的形式，因此令

由 于 初 态 |ψ〉在Bloch 球 中 对 应 的 向 量 为s:=[sin(2θ),0,−cos(2θ)]， 而算法最终欲得的 |B〉对应的向量为t:=[0,0,1]， 故 〈n|s〉=〈n|t〉 。 这说明s和t在Bloch 球面以n为轴的同一个的圆上，所以确实可以通过绕固定轴n进行多次旋转，把s转 到t。为了确定参数 ϕ和旋转次数k， 记r为s和t在n上的投影，如图1 所示，解析几何计算表明s−r和t−r之间的角度为 ω=π−2β。根据之前的推导，每作用一次G(ϕ,ϕ)相 当于绕转轴n旋 转 α =4β， 而 ω是所希望的总旋转角度，因此令ω =kα 可以求出 ϕ 与k应该满足关系式：

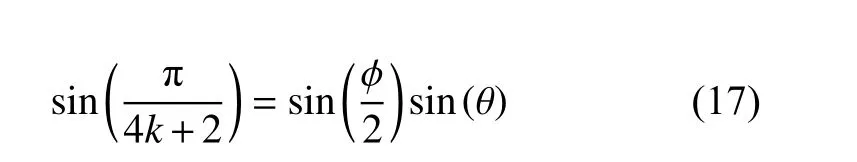
图1 在{ |A〉,|B〉}的 Bloch 球中，G (ϕ,ϕ)的多次作用相当于把初态 s 绕 转轴 n旋 转到目标元素的均匀叠加态t

容易验证，图2 和图3 分别展示了S f(φ)和Sψ(ϕ)的电路实现，其中最后一行为辅助qubit。注意到S f(φ) 需 要调用两次黑盒Of，因此表1 中后两种方法的黑盒调用次数是原始Grover 算法的两倍，不过这并不影响平方加速的数量级。

表1 3 种精确Grover 量子搜索算法

图2 S f(φ)的 电路实现，其中Of|x〉|b〉=|x〉|b⊕f(x)〉

图3 S ψ(ϕ)的电路实现

3 精确量子搜索的查询下界

3.1 目标元素占比未知时的查询下界

3.2 目标元素占比已知时的查询下界

在目标元素的占比已知的情况下，利用文献[14]的quantum angle 方法，并把它直接地扩展到多个目标元素的情形(即文献[15]文末提及的选取⎿N/M」个“不相交”数据库的思路)，可以证得精确量子搜索的查询下界为

4 结 束 语

本文梳理了3 种精确Grover 量子搜索算法，给出了算法流程、参数设置以及背后的几何直观，并指出它们都依赖于目标元素的占比，由此为出发点，说明了算法的最优性：对于目标元素占比已知的情况，3 种精确Grover 量子搜索算法已经达到最优；而对于目标元素占比未知的情形，精确量子搜索算法相比经典算法没有加速。因此本文对精确量子搜索算法给出了较为完整的概述。