铁路监视无人机宽带信息传输系统

张 斌

（国能朔黄铁路发展有限责任公司，沧州062350）

为保证行车安全及轨道各部件处于良好状态，延长轨道各部件的使用寿命，避免轨道设备因长期失修而造成的经济损失，须对铁路线进行监视及定期开展养护工作。随着运行体制的改革，铁路发展应以安全第一、效益优先为衡量标准[1]。因此，铁路巡检需要以有限的人力、先进的技术手段全面掌握和控制铁路沿线的情况。文献[2]结合计算机、图像监视、先进无线通信及自动化控制技术，在无线条件下实现了对铁路线路及周边的监视和数据传输。然而，室外摄像机覆盖范围小，无法从地面实现对铁路全线监控；文献[3]介绍了日本铁路运输公司线路设备检测装置的研发概况，提出了一种在营业车辆上安装检查轨道状态装置的监测方法。不过，受到列车编组、车速过高、安装不便等因素导致摄像机无法捕获铁路信息。受此启发，本文提出一种基于空基平台的铁路监视系统，以无人机作为摄像头的载体，多个无人机同时巡视铁路沿线，实时上传图像数据到一个高空飞艇中。

近年来，无人机产业迅速发展，得益于其灵活的移动性和低人力成本，无人机被广泛应用到通信、侦察、监视、遥感、航拍、灾害救援以及农业灌溉等各个领域当中[4-5]。空基平台的铁路监视系统相对于“地基”监视，其巡检方式更加灵活，但仍然要解决信息回传问题。由于要对铁路全线监视，图片多，数据量大，带宽要求在sub-6G 频段无法满足。为了缓解低频带频谱短缺，同时进一步提高系统通信和监视能力，最有效方法之一是利用毫米波波段[6]。与当前蜂窝波段（4G 或LTE）信号相比，毫米波信号会经历严重的路径损耗、穿透损耗和降雨衰落[7]。因此需要在飞艇接收端上采用大规模阵列天线进行波束赋形，得到指向铁路沿线无人机的波束进行定向接收。同时，在毫米波频段，较短的波长使得更多的天线能够压缩在同一尺寸中，从而允许大规模的空间复用和高定向波束赋形。

目前已有一些文献对微波波段系统的波束赋形进行了相关研究。文献[8]提出了一种应用于下行多输入多输出系统的三维波束赋形算法，进行了多用户分组和用户间干扰抑制；文献[9]提出了一种基于区域划分的三维波束形成策略，以保证所有用户都能获得公平的波束增益；文献[10]研究了高速铁路毫米波MU-MIMO 系统中的混合波束赋形设计，提出了一种发射端和接收端混合波束赋形的两级算法，在具有时延和多普勒效应的毫米波信道下依旧能够有很高的总吞吐量。在本文中，建立了无人机上行传输场景，对常用的两种不同微波波段系统波束赋形方法进行比较。并且对更优方案进行了拓展应用，为铁路沿线的无人机侦测部署提供参考。

1 系统模型

铁路沿线场景示意图如图1所示。在一段总长为L的铁路线中，分布有N个系留无人机，在整个铁路中段上方有一个飞艇作为基站。搭载平面阵列天线的基站需要服务目标区域内的无人机组，天线数为M。无人机用户与基站之间视为具有空间稀疏性的毫米波信道，由于链路中的遮挡和散射都比较弱，因此视距传输路径明显强于非视距传输路径[11]。因为地面障碍会严重影响视距传输路径，所以接收端不采用地面基站而是高空中的飞艇。受到毫米波波段中有限散射的影响，多径主要由反射引起。由于多径分量的数量通常较小，因此毫米波信道具有方向性并且在角度域中出现空间稀疏度。不同的多径分量具有不同的到达角。在不失一般性的情况下，采用定向毫米波信道模型，那么各个无人机与基站间的信道可以表示为[12-13]

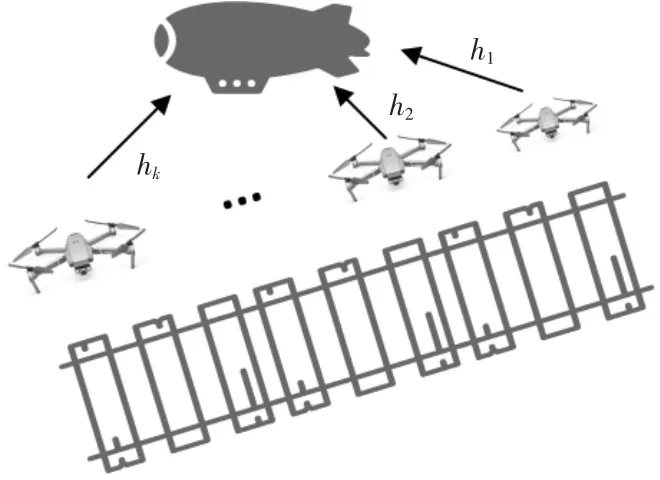
图1 铁路沿线场景示意图Fig.1 Schematic diagram of scenes along the railway

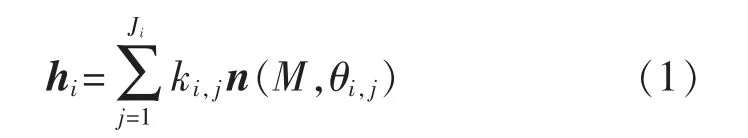
式中：k是传输路径的信道增益复系数；θ 是视距传输路径俯仰角的余弦值，下标i与j代表第i个无人机的第j个多径；Ji代表第i个无人机的总多径数，这其中包含1 个LOS 径以及Ji-1 个NLOS 径；n（M，θ）是指向向量函数，其定义为

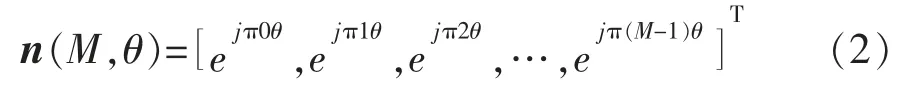
飞艇上的天线阵接收模型如图2所示。

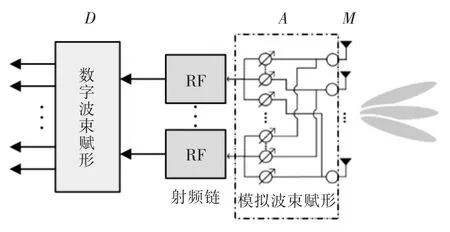
图2 系统模型Fig.2 System model

飞艇前端天线可以接收每个用户以功率P发送来的信号x。飞艇的接收机上共有M个天线，每根天线都与N个相位转换器相连，组成前端的模拟波束赋形。模拟波束赋形后连有N个RF 链（与无人机数相等），每个RF 链都接收来自各个天线的信号，最后进行数字波束赋形后，得到接收信号s。所以接收信号的表达式可以写为

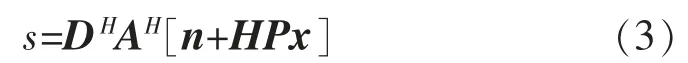
式中：H=［h1，…，hK］为信道矩阵；x=［x1，…，xN］T为N个无人机的数据；n为高斯白噪声；A为M×N列矩阵，代表模拟波束赋形；D为N×N矩阵，代表数字波束赋形；P为对角矩阵，对角线上为各个无人机的发射功率，如公式（4）所示：

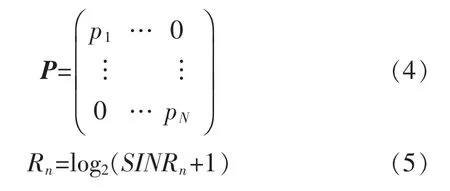
式中：

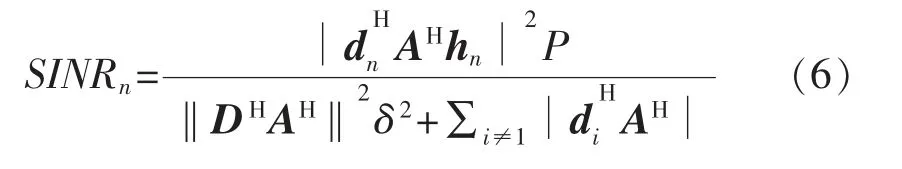
在得到接收信号的表达式后，就可以根据香农公式计算第k个无人机的可达率。因此，该场景问题描述为： 波束赋形设计适当的A和D两个矩阵，使得无人机的可达率之和最大。其中，为了增大模拟域的阵列增益，模拟波束赋形应当与信道相匹配，即A矩阵的每列的相位就是各个无人机信道相应的相位，如公式（7）所示：

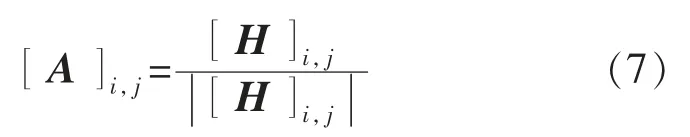
而常用的波束赋形设计方法可以分为迫零法（ZF）和最小均方误差（MMSE），下面将分别用这两种方法计算D矩阵，并且通过仿真进行比较二者的性能。

2 波束赋形设计

2.1 迫零法波束赋形设计

迫零法（zero-forcing，ZF）算法是线性预编码中最基础最简单的算法，在已知信道矩阵的前提下，可以消除多个信道间的干扰[14]。由于本文针对的是D矩阵进行迫零法波束赋形，因此需要把前端的A矩阵考虑为信道矩阵的一部分。所以，将数字波束赋形之前部分视为一个等效的信道H*为

在得到等效信道后，式（3）可以改写成式（9）所示：

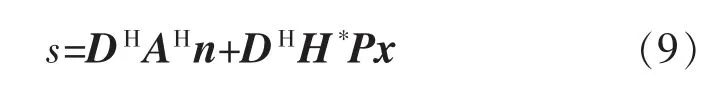
假设某个可行的矩阵，依据迫零法定义，矩阵应满足：

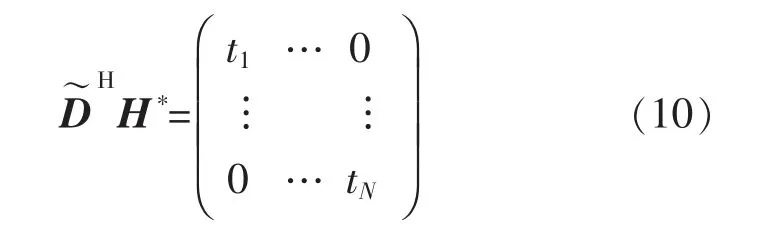
这样能够使得式（9）的前一项的系数矩阵为对角矩阵，从而消除用户间的干扰。其中t1，t2，…，tN为实系数。接着观察式（6）可以发现，在计算各个无人机的可达率时，式（10）对角线上的系数均被抵消，因此可以直接令的共轭转置等于H*的伪逆矩阵，并且接收信号与无人机可达率的表达式重新改写如下：

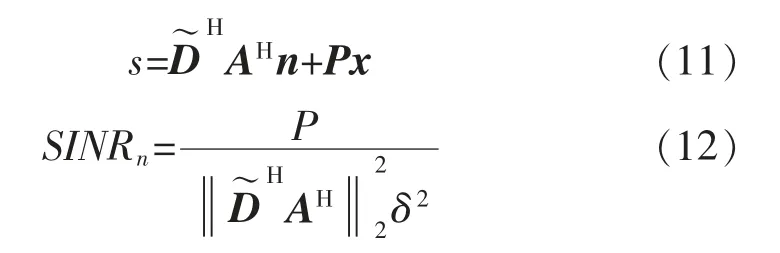
2.2 最小均方误差法波束赋形设计

基于最小均方误差（minimum mean square error，MMSE）准则的波束赋形技术基本原理同MMSE 预编码一致[15]，是一种让接收数据尽可能接近发送数据的一种方法，这一方法能够有效保证各个用户的公平性。所以MMSE 的目的就是找一个矩阵，来让s更加接近x。依据MMSE 定义，将接收信号与发射信号作差后取均值，由式（9）可得：

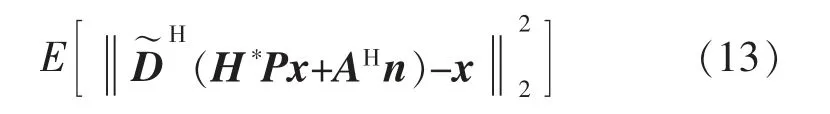
如果要求式（13）的最小值，需先将上式对D矩阵进行求导，然后令导函数为零得出D矩阵的解。这里，假设各个无人机的发射功率相等且均为P，对式（13）求导可得：

式中：

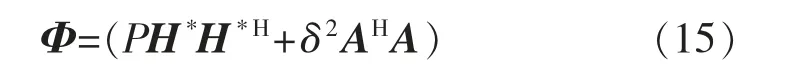
3 仿真

在仿真中，采用如公式（1）所示的信道模型。其中LOS 径信道增益复系数ki，j的幅度与距离成反比，并且设定当飞艇与无人机相距20 km 时，ki，j的平均强度为1。另外假定有4 个N-LOS 径，每个复系数都通过高斯随机函数生成，但是会比LOS 径的增益小20 dB。无人机与飞艇的高度差h为20 km，无人机总数N为6，无人机侦察的总铁路线长度L为100 km。两种方法的仿真结果如图3 和图4所示。

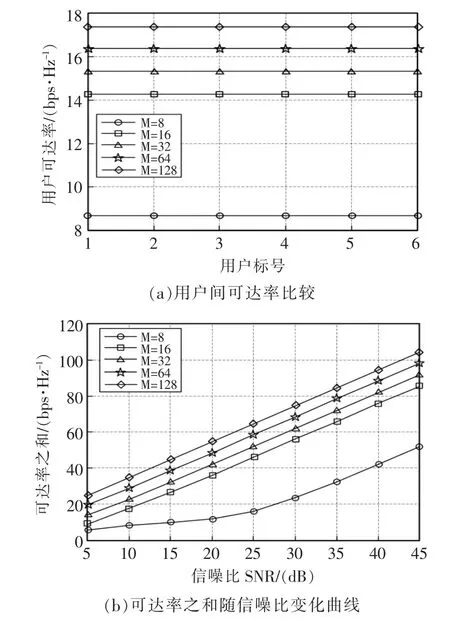
图3 最小均方误差法波束赋形仿真结果Fig.3 Beamforming simulation results of minimum mean square error method

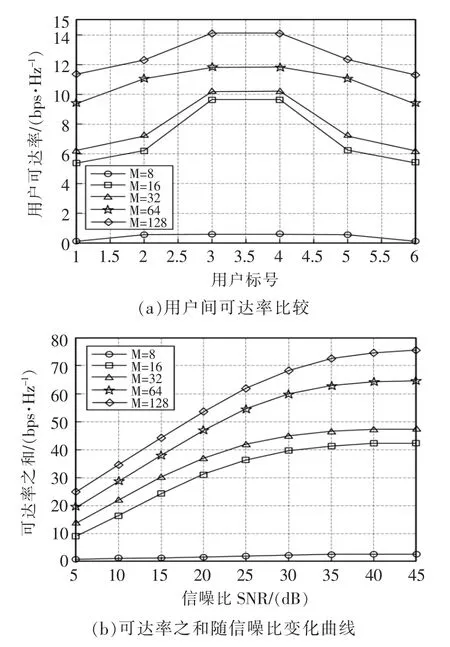
图4 迫零法波束赋形仿真结果Fig.4 Zero-forcing beamforming simulation results

整体比较图4 与图3 可知，最小均方误差法设计的波束赋形要优于迫零法。从可达率之和曲线上看：最小均方误差法几乎呈现出5 条平行线，天线数的增加和信噪比（SNR）的上升都能明显提升可达率；而迫零法的各个曲线相比更稀疏一些，随着天线数增加，可达率并不是跟着线性增加。而且随着SNR 的上升，曲线也有趋于渐缓的趋势，说明迫零法在高信噪比时可能会出现饱和情况。右侧部分则展示了在SNR 为40 的情况下，各个无人机的可达率曲线。可以看出在图3 中各个天线数的情况下都是一条水平的直线，说明最小均方误差法使得各无人机的可达率几乎相等，能够很好地保证各个无人机间的公平性。这是因为MMSE 法追求接收信号与发射信号误差最小，而与用户的位置无关。而该波束赋形下的公平性，正好可以保证无人机在任何位置巡检都不影响其上传数据。

总体而言，迫零法的复杂度较低、实现简单，虽然可以消除多个信号间的干扰，但在运算过程中忽略了噪声的影响，导致可达率下降。而最小均方误差法波束赋形具有公平性，能够很好地适应空基平台监视系统。

此外，在采用最小均方误差法的基础上，本文还对无人机的最佳数量进行了探究。在固定长度的铁路线上，无人机数目对总可达率的影响如图5所示。由图可知，部署越多的无人机，能够传输更多的信息。但是更多的无人机意味着更多的能量消耗以及RF 链路的需求。

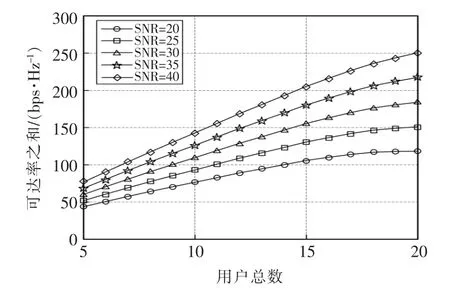
图5 无人机数对总可达率的影响（MMSE）Fig.5 Impact of the number of drones on the total reachability（MMSE）

无人机数对能量效率的影响如图6所示。能量效率为总消耗功率和总可达率的比值，其中总消耗功率包括基站上的接收机功率，和所有天线、相位转换器的功率等。

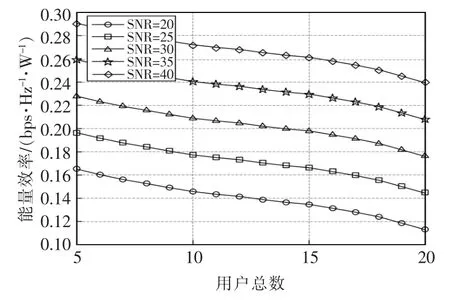
图6 无人机数对能量效率的影响（MMSE）Fig.6 Impact of the number of drones on energy efficiency（MMSE）

4 结语

本文提出了一种基于空基平台的铁路监视系统，建立了铁路无人机巡检的上行传输场景，并在系统的接收端进行波束赋形设计。分别用迫零法和最小均方误差法计算了数字波束赋形矩阵，并且通过仿真比较了二者的传输性能。仿真结果表明，最小均方误差法所设计的波束赋形使得无人机的可达率更高，同时还能够很好地保证公平性。随着无人机的增加，能够确保信息可传输的容量稳定增加。但是，太多的无人机反而会降低总的能量效率，因此需要根据无人机巡检的速度以及铁路长度来确定无人机数量。