基于混沌灰狼优化算法的栽植机四杆机构优化设计
2022-05-27李树森刘陈惠子邬博文
李树森, 刘陈惠子, 邬博文
(东北林业大学,黑龙江 哈尔滨 150040)
农林业生产是保证人类生存发展的第一要素[1]。近年来,随着我国人口的不断增长,快速提升农林业生产能力成为一项必须完成的重要任务[2]。移栽机械化能够克服传统人工作业劳动强度大、效率低的局限性,有效提升作物的产量与品质。本文拟对栽植机四杆机构的优化设计问题进行研究,四杆机构可以按照预设运动规律实现移动、摆动及转动等各种复杂的功能,具有运动精确度高、行程远、磨损小的特点[3]。在实际应用中,构件的尺寸决定了四杆机构的运动规律,是机构的主要误差来源。由于机构的运动规律与构件参数之间存在着复杂的非线性关系,这使得该机构的优化设计成为一项有挑战性的课题。
近些年来,研究人员通过运动轨迹、受力分析等方法对栽植机的结构参数进行优化[4-7]。这些方法都取得了较好的效果,但需要相关机构与环境的额外数理知识。针对此问题,智能优化算法被应用于连杆机构的设计优化[8-10],该方法不依赖于目标问题的具体模型,具有较好的鲁棒性与灵活性[11]。申屠留芳等将遗传算法用于红薯四杆栽植机构的优化设计,所得设计结果较传统的MATLAB求解器具有更好的偏差率。秦璐等将模拟退火算法用于摆缸八杆机构的角度与长度设计,展现了较好的全局搜索性能。沈明秀[12]等用粒子群算法优化平面四连杆的运动参数,优化后的机构能输出更小的角加速度与线加速度。
本研究针对栽植机四杆机构设计问题,提出一种基于混沌灰狼优化算法的优化设计方法。首先以四杆栽植机构为研究对象建立了轨迹误差最小化的优化模型。其次提出了一种混沌灰狼优化算法,通过嵌入混沌初始化、混沌扰动与自适应非线性算子来增强搜索能力。最后将所提方法应用于栽植机四杆机构的优化设计,验证本文方法更适用于栽植机四杆机构的优化设计。
1 数学模型
栽植机四杆机构简化图如图1所示,ABCD为平面四杆机构,杆AB为伺服电机驱动的驱动杆,杆BC为连杆,杆CD为摇杆,杆AD为机架。本文将四杆栽植机构的原点选择为A点,建立直角坐标系并根据预设的理想轨迹取8个离散点位。要求当杆AB转动一周时,连杆BC上的点M完成图上的轨迹,离散点位见表1。其中,i为离散点序号,Sxi和Syi分别为理想轨迹的x轴和y轴坐标,θi和Δθi分别为输入角及其变化量。
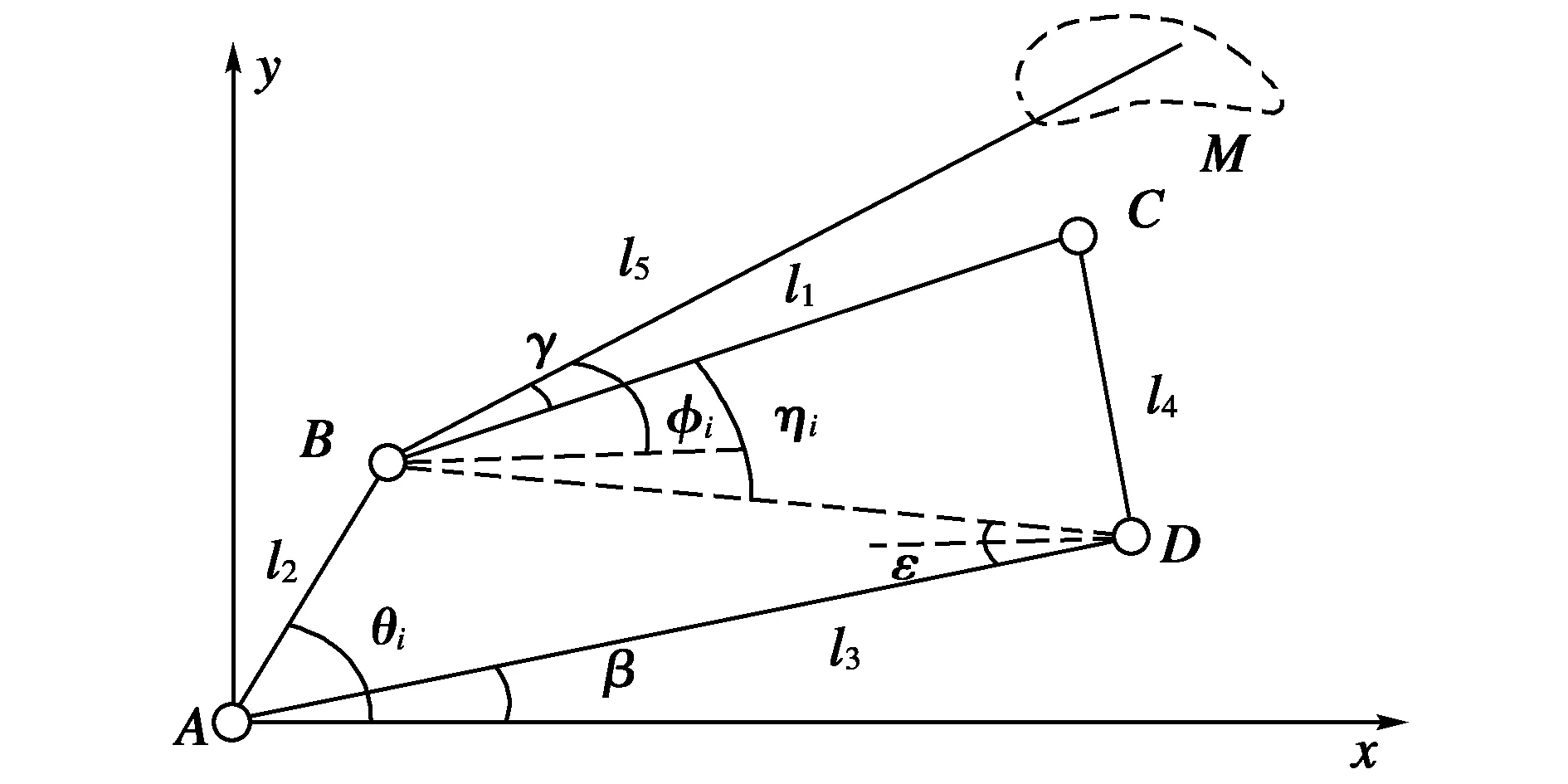
图1 栽植机四杆机构简图
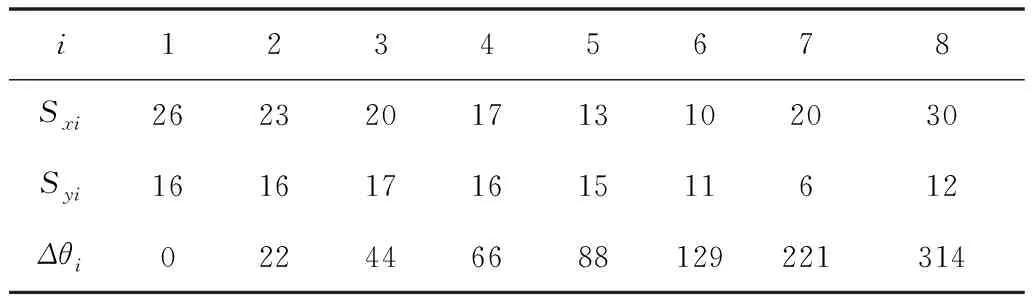
表1 理想轨迹运动坐标
1.1 设计变量
由图1所示的几何关系可知,当A点位置固定时,连杆BC上的点M的轨迹主要取决于各连杆的长度l1,l2,l3,l4,l5和角度参数β,γ,θ0。其中,β为AD与x轴的夹角;γ是BM与BC的夹角;θ0是AB与AD的初始角度;φi为BC与x轴夹角;εi为BD与AD夹角;ηi为BC与BD连线的夹角。故设计变量为:
X=[x1,x2,x3,x4,x5,x6,x7,x8]
=[l1,l2,l3,l4,l5,β,γ,θ0]
(1)
由图中几何关系可知:

1.2 目标函数
优化设计的目标是使点M的运动轨迹尽可能与预设轨迹相符合,可以理解为与离散点间的位置偏差最小化,因此目标函数按照点M的坐标(Mxi,Myi)与理想点坐标(Sxi,Syi)的误差均方根建立,即:
(2)
1.3 约束条件
根据实际设计需求,得到如下约束条件[13-14]:

10≤l5≤30⟹g13(X)=10-x5≤0
g16(X)=x6-30≤0
-0°≤γ≤15°⟹g17(X)=0-x7≤0
g18(X)=x7-15≤0
0°≤θ0≤60°⟹g19(X)=0-x8≤0
g20(X)=x8-60≤0
综上所述,本次优化设计的数学模型为:
2 混沌灰狼优化算法
2.1 灰狼优化算法
灰狼优化算法通过模拟灰狼群捕猎的行为来实现优化搜索。灰狼群是位于食物链顶端的捕食群体,具有严格的社会等级制度,通常由4种地位的狼组成:α、β、δ和ω。前三者作为族群内的精英个体,在搜寻猎物时距离猎物的距离依次递减,而ω作为普通个体,将跟随精英个体进行搜寻。算法步骤可简单概括如下:
包围机制:灰狼捕猎过程中首先会对猎物进行包围,数学描述为:
D=|C·X*(t)-X(t)|
(3)
X(t+1)=X*(t)-A·D
(4)
式中:t为当前迭代次数;X*(t)为群体最优解位置;X(t)为个体位置;A和C为系数向量,A=2a·r1-a,C=2·r2,r1和r2为0-1范围内的随机数;a是从2线性减小到0的常数。
狩猎机制:ω跟随α、β、δ的引导进行狩猎,其位置更新方式描述为:
X1=Xα-A1·Dα
(5)
X2=Xβ-A2·Dβ
(6)
X3=Xδ-A3·Dδ
(7)
(8)
式中:Xα、Xβ、Xδ为α、β、δ的位置;X1、X2、X3为方向向量;A与D的设置与包围机制相同。
2.2 Tent混沌初始化与扰动
混沌序列是一种非线性动力现象,其主要特点是具有遍历性、随机性和规律性[15]。在求解优化问题时,与基本上依赖概率的随机搜索相比,混沌序列可以更快地执行整体搜索。因此,混沌被应用于各种优化算法中[16-17],常见的混沌有Logistic映射与Tent映射。单梁等[18]证明了Tent映射的遍历均匀性和收敛速度均优于Logistic映射。Tent混沌映射的动力学迭代函数如下:
X(t+1)=X(t)/a,0≤Xn≤a (9) 式中:参数a∈[0,1]。 将所生成的混沌序列映射到优化目标的取值范围时即可作为初始化策略。除此之外,将混沌序列作为随机扰动算子引入算法,可以帮助算法克服陷于局部最优解的问题,提升寻优精确度。应用上式生成混沌序列Z,混沌扰动的数学描述如下: newX=min+(max-min)Z (10) 式中:max和min是变量的上下限,对个体进行混沌扰动的表达式为: newX′=(X′+newX)/2 (11) 式中:X′和newX′分别表示被添加扰动的个体和扰动后的个体位置。 灰狼优化算法的步长算子a是平衡其探索与开发的关键。原算法中a是线性递减参数难以满足实际优化情况,本文重新构造一种自适应非线性算子a(t)。 (12) 式中:amax和amin分别表示参数上下限;a1表示非线性部分;t表示当前迭代;Tmax表示最大迭代次数,f(p)表示个体适应度;ave表示种群平均适应度;β是自适应参数可按不同需要调整。 由上式可知a(t)由非线性部分a1和自适应部分β组成。一方面,非线性部分a1表现为前期函数下降缓慢,给全局探索充分时间;后期函数迅速下降收敛,加快算法收敛速度。另一方面,自适应部分β通过平均适应度评判每只狼的质量。对于较差的个体调整其搜索方向来保持种群多样性;对于较好的个体则减小步长来开发周边更好的解,从而增强收敛精度。 实验在4.40 GHz CPU和12 GB内存的PC机、Windows 10操作系统和MATLABR2016b环境中进行。应用混沌灰狼优化算法对上述栽植机四杆机构的模型进行优化设计,在给定的约束条件下,本文算法最终得到的各变量最优尺寸参数为: 其目标函数值为f(X*)=0.540 3。为了公平比较,在固定的数学模型下,与文献[13]中通过MATLAB迭代求解的结果f′(X*)=0.620 6相比,显然本文方法所优化得到的设计参数具有更小的目标函数值,这表示本文方法设计的栽植机四杆机构的构件尺寸参数更加合理,整体机构具有更小的轨迹偏差。 本文提出了一种基于混沌灰狼优化算法的栽植机四杆机构优化设计方法。首先,以栽植机四杆机构为研究对象,建立了轨迹误差最小化的函数优化模型。其次,提出了一种混沌灰狼优化算法。新算法嵌入了混沌初始化与扰动机制并设计了一种非线性自适应算子,分别用于增强原方法的多样性、跳出局部能力以及平衡探索与开发。最后,将所提方法应用于求解栽植机四杆机构的优化模型,并与传统的MATLAB求解工具相比较。实验结果表明,本文方法设计的栽植机四杆机构具有更合理的参数尺寸,其运动偏差仅为迭代求解方法的87%。在未来,将会继续研究更高效的优化方法,并应用于更复杂的农林业机构设计问题中。
X(t+1)=(1-X(t))/(1-a),a2.3 自适应非线性算子
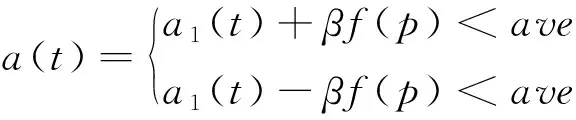
3 机构优化实验
4 结论
