外转子轮毂电机温度场及温度应力研究

周志刚，杨文豪，李争争，李豪迪

(1. 河南科技大学 车辆与交通工程学院，河南 洛阳 471000； 2. 宁波圣龙(集团)有限公司，浙江 宁波 315100； 3. 吉林大学 汽车仿真与控制国家重点实验室，吉林 长春 130012； 4. 同济大学 汽车学院，上海 4201804)

0 引 言

轮毂电机电动汽车作为纯电动汽车的一种，因传动效率高、转向灵活和响应速度快等优势逐渐受到社会各界重视[1-2]。轮毂电机在运行过程中，由于所处空间狭小空气流通困难、运行工况复杂以及损耗较高等原因，容易造成电机温度过高[3]。轮毂电机温升过高会影响效率和使用寿命，所以对外转子轮毂电机采取针对性冷却。不同冷却方式对外转子轮毂电机各部位的冷却效果不同，有必要对轮毂电机不同冷却方式的温度场与温度应力进行分析与研究，保证电动汽车的使用寿命与安全运行[4-5]。

国内外学者对电机温度场与温度应力研究相对较多。上官漩峰等[6]针对永磁同步感应电机温升影响永磁转子永磁体性能的问题，研究了双转子双鼠笼永磁感应电机的电磁场模型和三维温度场模型；王晓远等[7]针对冷却方式中螺旋型水路进行了流体动力学分析；王小飞等[8]针对车用永磁同步电机，从流速、压差、温差等多方面对比螺旋型、轴向Z字型、径向Z字型3种冷却水道对轮毂电机温度的影响，并分析不同流速时电机温升情况；司纪凯等[9]对表面-内置式永磁同步电机进行温升计算，并分析了不同工况下温度场的变化情况；丁树业等[10]针对永磁同步电机进行了温度场与温度应力分析，得到电机各部位形变不仅受温升作用影响，还受结构和施加约束等因素影响。综上，现有文献主要对永磁同步电机的温度场以及温度应力方面进行研究，对电动汽车中轮毂电机温度场与温度应力研究相对较少，特别缺少对轮毂电机中采用不同冷却方式的温度场与温度应力研究。

笔者以外转子轮毂电机为研究对象，建立外转子轮毂电机仿真模型，对额定工况条件下运行的轮毂电机进行电磁仿真，并进行磁、热耦合分析，对比不同冷却方式条件下轮毂电机温度场。考虑不同冷却方式对电机各部位形变影响，通过台架实验将实验数据与有限元仿真数据进行对比，验证有限元方法的正确性，同时确保轮毂电机温度应力场载荷设置的正确性。

1 轮毂电机模型

以一台8 kW车用轮毂电机为研究对象建立模型，其结构为外转子永磁同步电机。轮毂电机结构如图1，基本参数如表1。

图1 轮毂电机模型Fig. 1 In-wheel motor model

表1 轮毂电机基本参数Table 1 In-wheel motor basic parameters

对轮毂电机分别单独采用水冷、风冷和油冷进行温度场研究。

水冷冷却是通过电机机壳内部开槽水道，利用热传导将电机各部件中的热量传递至机壳，通过冷却水将电机内部热量带走达到冷却目的，外转子轮毂电机冷却水道如图2。风冷冷却是通过电机内部与外部气流对各部件进行自然对流冷却。油冷冷却是通过在电机内部填充冷却油，使冷却油在电机内部流动，利用冷却油良好的导热性能直接对电机各部件进行冷却。表2为轮毂电机材料导热系数。

图2 轮毂电机水道模型Fig. 2 In-wheel motor waterway model

表2 轮毂电机材料基本参数Table 2 Basic parameters of in-wheel motor material

2 温度场相关系数

2.1 轮毂电机损耗

电动汽车轮毂电机热源主要来自于电机内部各种损耗。轮毂电机内部损耗主要包括铁芯损耗、绕组损耗、永磁体涡流损耗以及机械损耗等，因机械损耗计算条件较为复杂，且在各种损耗中占比较小，因此不对机械损耗进行重点研究[11]。

绕组损耗PCu计算如下：

PCu=3(I2R)

(1)

式中：I为轮毂电机中绕组电流；R为轮毂电机中绕组电阻。

定子和转子铁芯损耗主要分为磁滞损耗与涡流损耗，计算定子和转子铁芯损耗需计算磁滞损耗与涡流损耗。

定子和转子铁损PFe计算如式(2)、式(3)：

PFe=Ph+Pc

(2)

(3)

式中：Ph为电机铁芯磁滞损耗；Pc为铁芯涡流损耗；Bm为磁通密度；f为交变频率；kh、kc分别为铁磁材料的磁滞损耗系数和涡流损耗系数。

永磁体涡流损耗Pe计算公式如式(4)：

(4)

式中：vm为轮毂电机中永磁体体积；J为轮毂电机中永磁体电流密度；σ为轮毂电机中永磁体电导率。

针对外转子轮毂电机电磁场进行仿真分析，得到各种损耗结果如图3。由图3可知：电机定子和绕组部件损耗密度分布较高，永磁体涡流损耗和转子损耗次之。

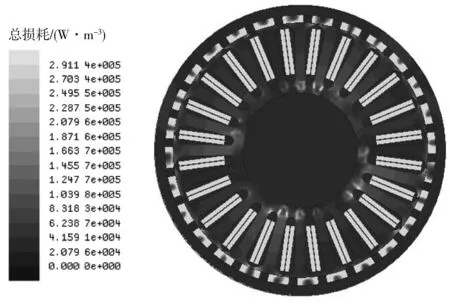
图3 轮毂电机损耗分布云图Fig. 3 In-wheel motor loss distribution cloud map

2.2 轮毂电机热场数学模型

在直角坐标系下，根据导热基本定律，轮毂电机瞬态温度场求解为式(5)边值问题：

(5)

式中：kx、ky、kz分别为轮毂电机各材料在x、y、z方向的导热系数；T为电机温度;q为热源密度;h为边界sj的对流散热系数；n为si、sj边界面上的法向矢量；K为si、sj边界面上的法向热传导系数；T1和T0分别为边界面与周围介质的温度；si为轮毂电机绝热面边界情况，主要包括：槽中心断面以及电机各部件的轴向中心面；sj为轮毂电机散热面边界情况，包括：定子铁芯端面、永磁体外表面、绕组表面、转子轴向端面以及机壳表面。

2.3 轮毂电机传热边界条件

电动汽车在运行过程中，轮毂电机内部损耗转化为热源，使电机温度升高。流体与固体间的散热系数以及电机内部的材料导热系数对电机温度影响较大。

绕组的散热系数hci为：

(6)

式中：Nuc为绕组努塞尔特常数；det为绕组的等效直径；λair为空气导热系数。

定子铁芯的散热系数hsh计算公式为：

(7)

式中：vr1为转子表面线速度。

转子铁芯的散热系数hrh计算为：

(8)

(9)

式中：Nur为转子铁芯努赛尔特常数；RR为转子铁芯外径；Re为转子铁芯端面气隙雷诺数；n1为电机额定转速；γ为空气运动粘度系数。

机壳表面散热系数hca计算为：

(10)

式中：vair为电机机壳表面空气运动速度(按照电机壳旋转速度的75%取值)。

电动汽车在行驶过程中，电机转子与定子之间的空气产生流动，因此转子内侧与定子之间的气隙存在对流换热，气隙间对流换热系数βδ为：

(11)

式中：Vδ为气隙空气平均速度。

定子槽内绕组等效导热系数为：

(12)

式中：δCu为绕组铜裸线直径；δj为铜线绝缘漆厚度；λj为绝缘漆等效传热系数；λCu为绕组铜导线的传热系数。

3 轮毂电机不同冷却方式温度特性

依据第1节模型的建立，进行轮毂电机额定工况的仿真分析，进行三维电磁场与温度场耦合仿真计算，并分别进行风冷、水冷及油冷冷却方式仿真分析。

3.1 风冷轮毂电机温度特性

工作环境为20 ℃，风冷冷却时，得到仿真结果如图4～图6。轮毂电机温度变化曲线如图4。由图4可知：电动汽车在运行过程中轮毂电机各部件温度随时间增加而逐渐上升，在3 000 s前温度上升速度较快，在3 000～4 000 s之间，电机温度上升趋势逐渐减小，电机绕组温度在达到119 ℃时逐渐趋于平稳，运行4 000 s后轮毂电机各部件温度曲线逐渐趋于稳定，且电机绕组与定子温度逐渐接近。

图5为轮毂电机整体温度分布以及各部件温度分布。由图5可知：在轮毂电机运行过程中，绕组温度最高，定子次之；由于受到通风条件的限制和绕组损耗过高影响，定子齿部温度高于定子轭部；永磁体与转子的损耗较低并且有良好的通风位置，永磁体和转子温度最低。

图4 轮毂电机各部件温度变化曲线Fig. 4 Temperature variation curve of various components of the in-wheel motor

图5 风冷轮毂电机整体温度场分布Fig. 5 In-wheel motor overall air cooling temperature field distribution

图6为轮毂电机整体沿径向温度变化分布。由图6可知：因为定子齿部与绕组相邻，受到绕组温度影响较大，而定子底部与电机轴部相接触，在一定程度起到冷却作用，电机定子径向区域相对于轴向区域温差较大；由于转子径向长度较小，受到周围热源影响较小，转子区域轴向与径向温差相对较小。

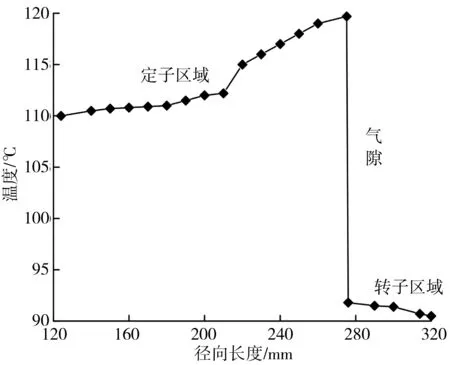
图6 轮毂电机整体沿径向温度变化Fig. 6 Temperature variation of the in-wheel motor changing along the radial direction

3.2 水冷轮毂电机温度特性

轮毂电机采用水冷方式时，电机整体以及各部件温度分布如图7。结合图7及图5可知：采用风冷冷却时，轮毂电机内部最高温度约为119 ℃，高温区域主要集中在绕组与定子齿部；采用水冷冷却时，电机各部件温度都有所下降，最高温度约为79 ℃，下降了40 ℃，虽然高温部件仍是绕组与定子，但是定子齿部高温区域明显减少。

图7 水冷轮毂电机整体温度场分布Fig. 7 In-wheel motor overall water-cooling temperature field distribution

3.3 油冷轮毂电机温度特性

轮毂电机采用油冷冷却方式时整体温度分布及各部件温度分布如图8。轮毂电机在油冷冷却时高温区域主要集中在定子和绕组，温度分别约为 84.6、81.2 ℃，低温部件为转子和永磁体，温度分别约为69.7、72.4 ℃；电机采用油冷冷却可有效降低电机整体温度，达到更好的冷却效果。

图8 油冷轮毂电机整体温度场分布Fig. 8 In-wheel motor overall oil-cooling temperature field distribution

4 轮毂电机温度应力与应变

4.1 温度应力计算分析

轮毂电机受温度变化影响会产生温度应力发生形变。关于轮毂电机形变，研究多基于单电机平台，忽略车轮与车轴对电机的影响。由于轮毂电机技术是将电机安装于车轮内部，与单电机相关约束条件相差较大，因此对比分析轮毂电机与单电机的形变情况，并着重研究不同冷却方式中轮毂电机温度场对温度应力影响。

对轮毂电机进行温度应力分析，当认为形变小于相应部位尺寸时忽略高阶小量，温度应力关系式可表达为：

(12)

式中：B为单元应力矩阵；D为弹性系数矩阵；δ为系统位移向量；ε0为单元热应力矩阵；n2为单元数。

如果αx，αy，αz分别表示为x，y，z方向上的热膨胀系数，则ε0可表示为：

ε0=[αxΔt,αyΔt,αzΔt,0,0,0]T

(13)

式中：Δt表示温升。

由于单电机与轮毂电机在形变过程中受到的约束条件不同，因此对单电机和轮毂电机分别进行约束条件设置；根据轮毂电机特殊使用情况，在轮毂电机与轴部接触部分施加固定边界条件进行约束，并在转子与机壳接触部分施加固定边界条件进行约束；在单电机中对轴部与定子接触部分施加固定边界条件进行约束。关于对温度应力形变情况分析，均基于电机温度场的分布情况与边界条件的设定。

4.2 风冷冷却对轮毂电机形应变影响

风冷电机温度应力形变分布如图9。由图9可知：轮毂电机采用风冷冷却方式时，由于电机内部空气导热系数较低，不能及时使电机内部热量排除，电机定子、绕组等部件处于高温状态，造成电机部件形变较大。

单电机最大形变出现在定子齿部、绕组和转子等部件，最大值约为0.116 mm。轮毂电机最大形变情出现在绕组部分约为0.064 mm，相对于单电机最大形变下降了0.052 mm。但是从图9(b)处可以得到轮毂电机内部结构破坏程度大于单电机，说明轮毂电机的形变数值虽小，但由于轮毂电机安装在汽车轮毂中的特殊性，反而破坏大对结构影响较大。

图9 风冷电机温度应力形变分布Fig. 9 Air cooling temperature stress deformation distribution of in-wheel motor

轮毂电机受到约束作用不同，造成轮毂电机与单电机形变情况有较大区别，若将单电机的形变情况应用于轮毂电机中进行研究，可能导致形变计算不准确，从而使轮毂电机寿命以及安全性受到影响，因此对轮毂电机采用不同冷却方式的形变分析，均基于轮毂电机环境下进行。

4.3 水冷冷却对轮毂电机形变影响

水冷轮毂电机温度应力形变分布如图10。由图10可知：采用水冷冷却方式的轮毂电机，在经过冷却后电机最大形变约为0.037 mm，相对于风冷冷却方式电机最大形变下降0.027 mm。这是由于冷却水具有较好的导热性，能将电机内部热量通过热传递方式进行传导，使温度应力对电机形变影响减小。

轮毂电机各部件受到温度应力影响较大，最大形变出现在绕组部分，这是由于绕组部分温度较高导致形变程度较大。最小形变出现在电机定子轭部与转子部件，这一方面是由于定子轭部与转子散热性能较好，另一面是由于相邻部件轴与永磁体温升较小。

图10 水冷轮毂电机温度应力形变分布Fig. 10 Water-cooling temperature stress deformation distribution of in-wheel motor

4.4 油冷冷却对轮毂电机形变影响

油冷轮毂电机温度应力形变分布如图11。由图11可知：采用油冷冷却时，电机最大形变同样出现在绕组区域约为0.039 mm，相较于风冷冷却下降了0.025 mm。电机定子区域形变变化相对较小，这是由于电机受到油冷冷却方式影响，电机内部温度下降，各部件形变减小。

图11 油冷轮毂电机温度应力形变分布Fig. 11 Oil-cooling temperature stress deformation distribution of in-wheel motor

4.5 温度应力对定子影响

电机定子温度应力形变分布如图12。由图12可知：风冷单电机中定子形变最大达到0.103 9 mm，大于风冷轮毂电机定子的0.026 1 mm，这是因为轮毂电机的特殊结构对电机形变造成一定限制，使轮毂电机定子形变小于单电机定子。

虽然不同冷却方式对定子形变影响不同，但是定子形变趋势与温度变化趋势基本相近，均是轭部到齿部逐渐增大，最大形变差值达到0.089 0 mm；其中温度对电机形变有较大影响，风冷轮毂电机定子最大形变约为0.026 1 mm、水冷轮毂电机和油冷轮毂电机定子最大形变较小分别约为0.015 4、0.018 0 mm；定子轭部部分没有发生形变，是因为受到电机轴部约束。

图12 定子温度应力形变Fig. 12 Stator temperature stress deformation

4.6 温度应力对绕组影响

绕组温度应力形变如图13。由图13可知：在3种冷却方式中风冷轮毂电机绕组形变程度最高，约为0.063 9 mm，这是由于风冷轮毂电机绕组在3种冷却方式中热源聚集程度最高； 3种冷却方式中绕组形变分布规律相同且与温度分布特性关系密切。

4.7 温度应力对永磁体影响

永磁体温度应力形变分布如图14。结合图14及图6～图8可知：风冷轮毂电机相对于油冷轮毂电机和水冷轮毂电机，永磁体温度相差较大，但是永磁体形变程度相差较小，其中风冷轮毂电机最大形变约为0.023 7 mm、水冷轮毂电机最大形变约为0.014 1 mm、油冷轮毂电机最大形变约为0.016 8 mm。

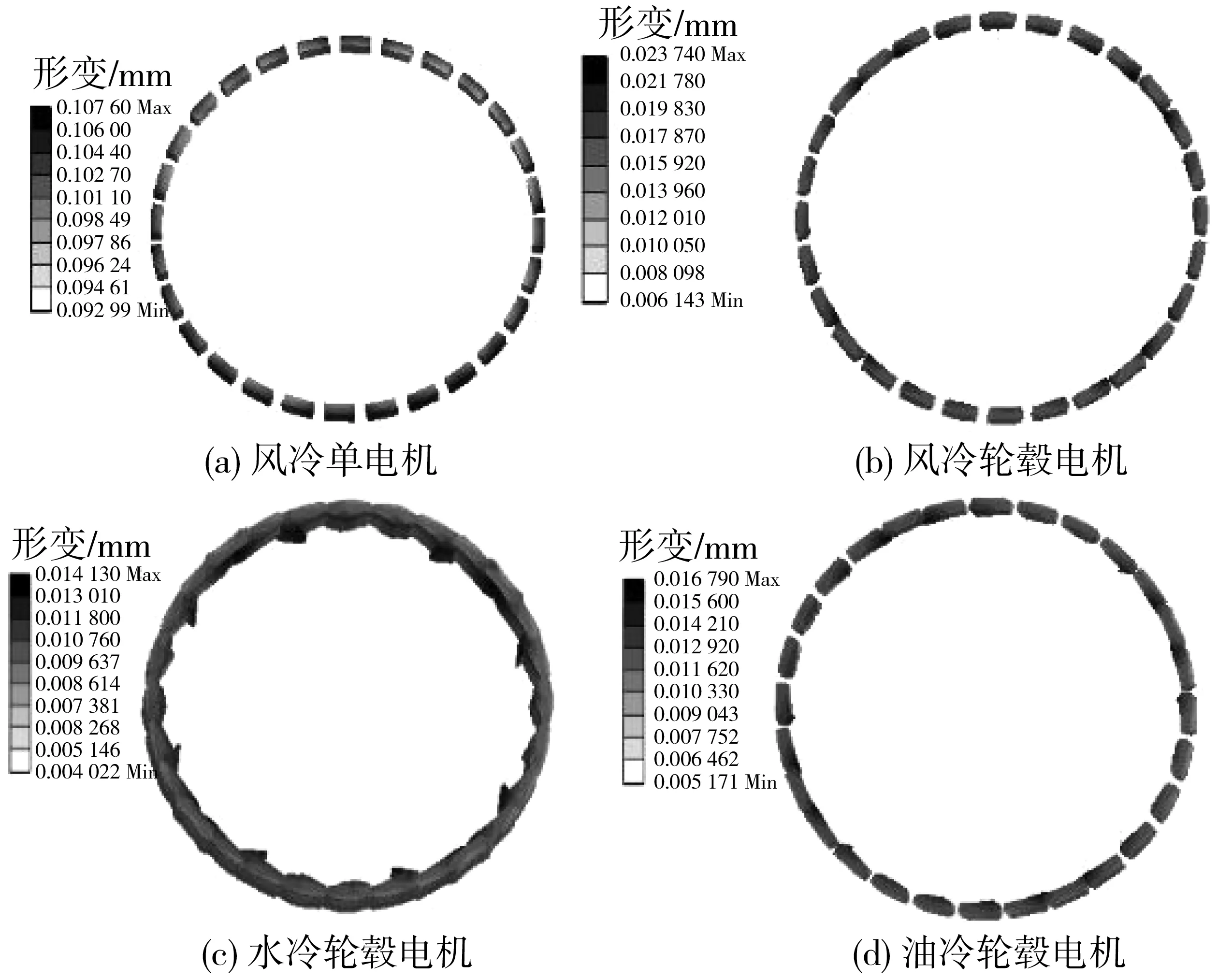
图14 永磁体温度应力形变Fig. 14 Permanent magnet temperature stress deformation

4.8 温度应力对转子影响

电机转子温度应力形变如图15。在电机中转子形变较小，风冷轮毂电机最大形变为0.016 2 mm，水冷轮毂电机最大形变约为0.009 3 mm，油冷轮毂电机最大形变约为0.011 3 mm，且形变皆是沿径向发生变化，轴向形变几乎没有发生变化，这是因为转子形变与温度分布关系密切；同时由于轮毂电机与单电机中转子受到约束条件不同，所以轮毂电机与单电机中转子形变变化趋势相反，且单电机形变远大于轮毂电机，风冷时转子最大形变相差0.099 8 mm。

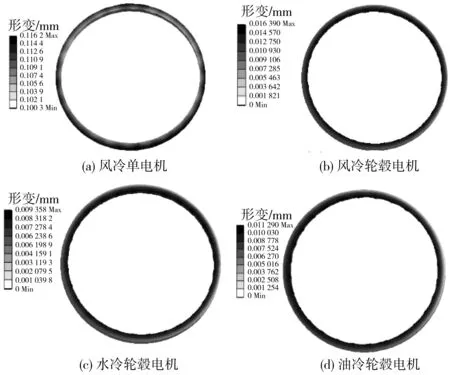
图15 电机转子温度应力形变Fig. 15 Motor rotor temperature stress deformation

5 试验验证

对轮毂电机进行风冷冷却方式的温升试验，并将试验结果与温升仿真计算结果对比，完成有限元模型的验证，图16为轮毂电机温升实验装置。主要由轮毂电机、驱动控制器、负载电机、轮毂电机性能测控平台、测功机、电源、温度传感器和红外线测温仪等装置组成。在电机绕组中安装温度传感器用于检测电机温度，红外线测温仪测量转子表面温度。

图16 轮毂电机温升实验装置Fig. 16 Experimental device of in-wheel motor temperature rise

在对轮毂电机进行温升实验时，通过温度传感器和红外线测温仪测试读取测点温度，并与有限元计算结果进行对比。外转子轮毂电机计算温度与实验测试温度对比曲线如图17。

由图17可知：绕组和转子温度计算值与试验值吻合度较好，但是由于所受实验本身的多方面因素影响，计算温度与实验测试值存在一定误差，最大误差为6.6%，结果在可控范围内，验证了所建立的轮毂电机有限元分析模型的正确性。

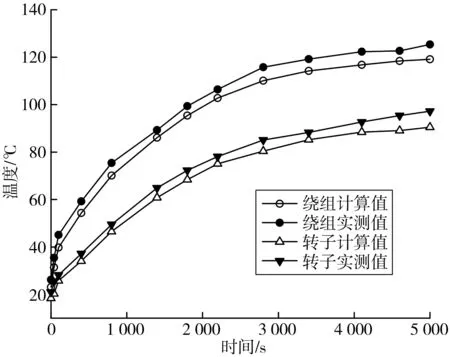
图17 电机实验温度与计算温度曲线(风冷冷却)Fig. 17 Motor experimental temperature and calculated temperature curve (air cooling)

6 结 论

对电动汽车轮毂电机在不同冷却方式下进行温度场对比分析，将不同冷却方式得到的温度场与温度应力耦合，探究了轮毂电机温度与温度应力之间的关系，并分别对比了单电机与轮毂电机的形变。虽然轮毂电机采用不同冷却方式对电机整体以及各部件温度场影响效果不同，但是定子绕组与转子仍分别为电机最高与最低温度部件；电机采用风冷方式时整体温度最高并且电机各部件温度相差较大，采用水冷方式时电机温度最低，对电机冷却效果明显但是相对于油冷温差较大。通过实验数据与计算结果进行对比，验证轮毂电机模型建立的正确性，并为轮毂电机采用不同冷却方式温度场和形变研究提供基础。在此基础上，进行了不同冷却方式对电机形变影响分析，其中，风冷电机相对于水冷电机和油冷电机形变最大；水冷与油冷电机之间形变相差较小。由于约束条件不同使轮毂电机结构受到形变影响较大，并且单电机与轮毂电机之间最大形变不同。最后通过试验，验证了轮毂电机模型的正确性。