基于Chen-Young模型及不平衡推力法的降雨型高切坡稳定性演化过程分析
2022-05-27靳红华王林峰任青阳张星星
靳红华,王林峰,任青阳,张星星
(1. 重庆交通大学 山区桥梁及隧道工程国家重点实验室,重庆 400074; 2. 重庆交通大学 山区公路水运交通地质减灾重庆市高校市级重点实验室,重庆 400074; 3. 重庆文理学院 土木工程学院,重庆 402160)
0 引 言
近年来,我国基础设施建设快速发展,尤以三峡工程、溪洛渡水电站、乌东德水电站等大型水利工程大规模建设,随之而来的岩土边坡稳定性问题也与日俱增。以三峡库区为例,三峡工程及当地人类生活建设的不断开展,不可避免地产生了大量人为高切坡,三峡库区地质构造及地形地貌条件复杂特殊,受当地经济发展、财政投资等因素限制,据统计,截止目前,仍有约1 000个高切坡仍缺乏有效的支护措施,这些高切坡受人为切坡、降雨等因素,一旦变形滑塌,将对长江航道安全运营、当地居民生命财产造成严重的威胁,因此高切坡防护是三峡库区地质灾害防治工作的重要组成部分,也是关系到三峡库区长治久安的大事[1]。
库区大量缺乏支护裸露在外的工程切坡为降雨型滑坡的产生提供了一定的物质来源,据统计,我国每年平均发生新老滑坡次数约3×105起,其中降雨型滑坡次数占滑坡总次数90%以上,当降雨条件(降雨类型、降雨强度、降雨历时)达到一定阈值时,该类边坡极易发生失稳破坏。已有研究多针对常见倾斜式工程切坡在自重及降雨作用下的失稳破坏,台阶状高切坡在降雨条件下的稳定性分析亟待解决,尤以砂土覆盖层基岩型台阶状高切坡在自重及降雨条件下其降雨入渗过程及稳定性演化过程研究逐渐成为该领域的研究热点及技术难题之一。
降雨型边坡稳定性演化过程定量分析主要包括边坡降雨入渗模型分析、降雨入渗数值模拟分析及边坡稳定性计算三部分。其中选取合理的降雨入渗模型是分析边坡降雨入渗过程的前提,其主要包括降雨模型试验及降雨入渗理论模型建立,如许旭堂等[2]、马吉倩等[3]通过建立室内相似边坡模型,采用人工降雨系统模拟降雨,分析了降雨入渗影响下边坡非饱和渗流特性,揭示了边坡降雨入渗过程;H. RAHADJO等[4]通过对天然残积土坡进行长期的现场监测与人工模拟降雨试验,系统研究了人工模拟降雨及天然降雨条件下土坡渗流特性。降雨入渗模型分析主要包括Green-Ampt模型及其改进模型Chen-Young模型等相关理论推导。降雨入渗数值模拟研究主要围绕揭示边坡降雨入渗过程及其失稳破坏过程为主,常用数值模拟软件如ABSQUS、SEEP/W、FLAC3D等,如任德斌等[5]通过有限元数值模拟软件建立边坡数值模型,模拟了不同工况下的边坡降雨入渗过程,获得了诸如孔隙水压力、位移、稳定系数的分布及变化规律,揭示了降雨作用下边坡的失稳机理。降雨型边坡稳定性计算则主要以前述降雨入渗模型为基础,建立稳定性计算与评价方法,如汪丁建等[6]基于Green-Ampt模型或Chen-Young改进模型建立了适用于降雨入渗条件下无限长边坡的稳定性理论计算与分析方法;A.W.SKEMPTON等[7]在降雨饱和并形成平行于坡面渗流前提下,基于无限长斜坡假定提出了边坡“顺坡平面”破坏模式,并建立了边坡稳定性计算方法;M.BORDONI等[8]从诱发滑坡的水文因素出发,利用现场观测调查数据建立了简化的降雨型滑坡稳定性分析方法;E.CONTE等[9]通过建立理想的边坡滑动模型结合实地调查建立了无限边坡在降雨入渗过程中的入渗深度及稳定系数评价方法;连继峰等[10]在此基础上讨论了有限长边坡且滑面为非直线的降雨型边坡稳定性分析方法,其假设浅层滑坡滑面呈“顺坡曲线”失稳模型,极大的丰富了降雨型边坡稳定性理论计算与分析方法。
以上研究多立足无限长倾斜式均土质边坡,且基于滑面平行于坡表假定,忽略了有限长高边坡具有台阶其坡面为非直线这一事实,且未考虑湿润锋深度与边坡形状尺寸的关系,导致其针对基岩型台阶状土质高切坡适用性较窄,该类高切坡降雨入渗过程及稳定性分析认识不足。基于此,笔者以常见砂土覆盖层两级台阶基岩型高切坡为研究对象,考虑降雨入渗深度与边坡形状尺寸的关系,基于Chen-Young改进模型建立该类降雨型高切坡理论模型,利用不平衡推力系数法对降雨条件下该类高切坡稳定性展开理论推导,同时选取不同降雨类型及降雨时间工况,利用Geo-studio数值模拟软件开展多工况下该类高切坡降雨入渗过程研究,揭示其稳定性演化过程。
1 降雨入渗分析
1.1 Chen-Young模型
Chen-Young假设坡面无积水且考虑边坡表面为斜面,见图1,其边坡降雨入渗速率如式(1)[11]:
(1)
式中:Ks为饱和渗透系数,m/s;z′f为降雨竖直入渗深度,m;α为边坡坡角,(°);Sf为湿润锋处的土壤水吸力,m。
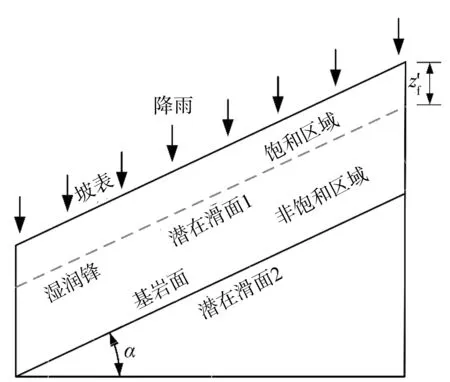
图1 Chen- Young改进模型Fig. 1 Chen-Young improved model
1.2 基岩型台阶状高切坡降雨入渗模型
1.2.1 假设条件
与均土质倾斜式边坡不同,基岩型台阶状高切坡由上部土层、下部不透水基岩层组成,其降雨入渗过程及稳定性演化过程因边坡自身形式特殊而异于一般边坡,因此笔者在文献[6]基础上基于Chen-Young改进模型建立基岩型台阶状高切坡降雨入渗模型,如图2,其基本假设条件为:①基岩为不透水基岩;②降雨强度大于土体饱和渗透系数,当降雨强度大于土体入渗率时,边坡表层坡体处于饱和状态;③潜在滑动面为湿润锋面或基岩面;④不考虑地下水水位。
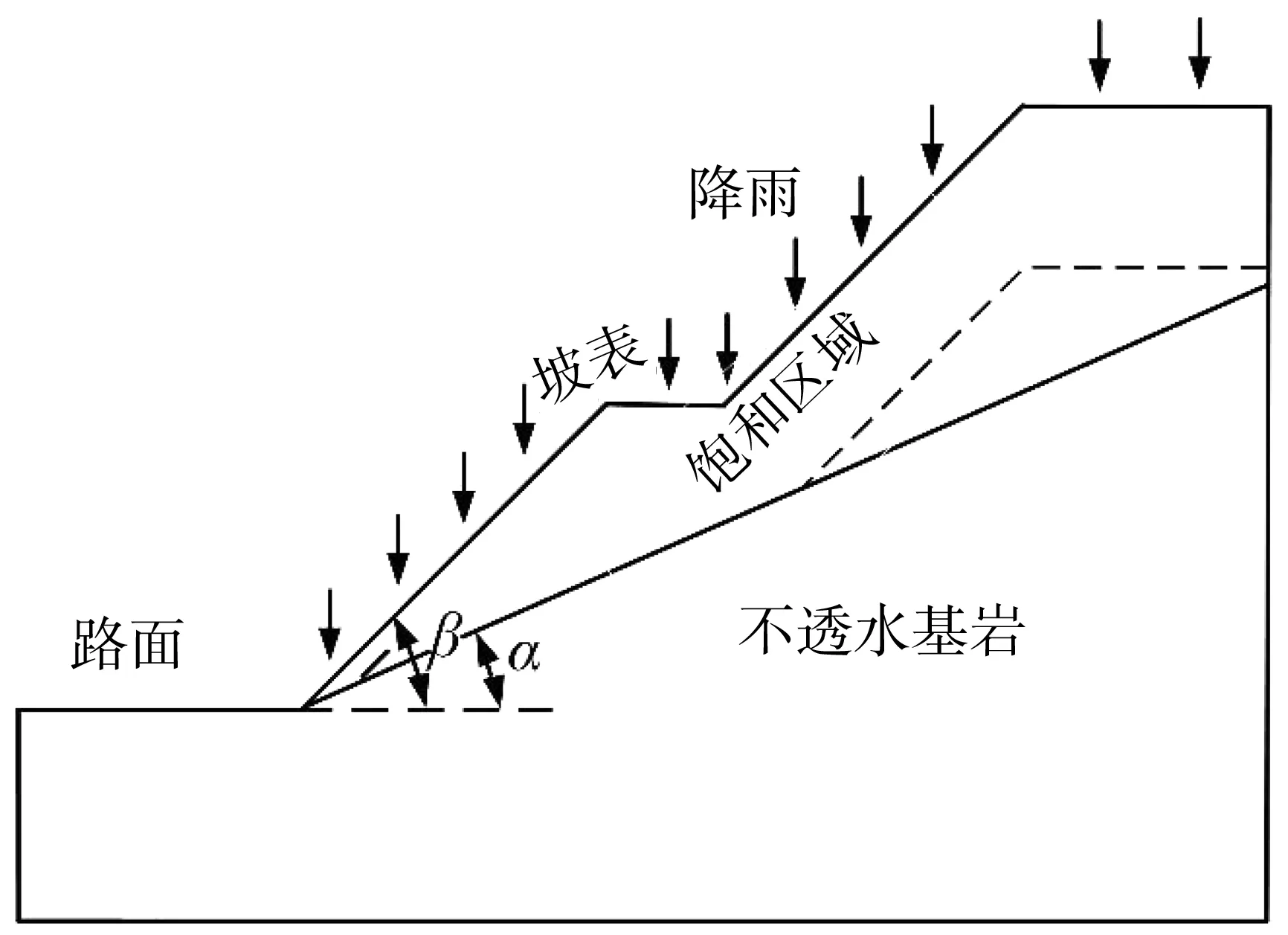
图2 基岩型台阶状高切坡降雨入渗理论模型Fig. 2 Theoretical model of rainfall infiltration of bedrock stepped high cut slope
1.2.2 入渗率及入渗深度求解
覃小华等[12]将边坡降雨入渗阶段划分为无压入渗、有压入渗和稳定入渗3个阶段。
1)无压入渗阶段
降雨初期,坡体入渗率小于降雨强度,坡体处于非饱和状态,此时入渗率i为:
i=qcosα
(2)
式中:q为降雨强度,mm/h。
该阶段内湿润锋深度zf随时间的变化为:
(3)
式中:Δθ为土体天然、饱和含水率之差。
2)有压入渗阶段
当t0时刻边坡坡体由非饱和状态过渡到饱和状态时坡体表层形成饱和带,此时入渗率i应采用式(1)。饱和带形成后,坡体入渗率为降雨强度在斜坡垂直面的投影,此时湿润锋深度z0为:
(4)
根据质量守恒,此临界时刻t0为:
(5)
由达西定律可知:
(6)
联立式(1)及式(6),且降雨入渗深度远小于边坡长度,认为Sf≥z′f,可得该阶段内入渗深度随时间的变化可简化为:
(7)
积分式(7)可得由降雨入渗引起的湿润锋推进变化率为:
(8)
汪丁建等[6]在此基础上考虑饱和带形成后渗流使得湿润锋深度减小这一事实使得降雨入渗分析更加准确,其推导湿润锋相对减小深度为:
(9)
式中:l为斜坡长度,m。
式(7)减去式(9)即为实际湿润锋扩展速率:
(10)
积分式(10)并代入初始条件t=t0,zf=z0可得该阶段内湿润锋随时间变化关系为:
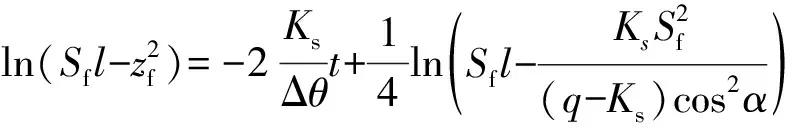
(11)
3)稳定入渗阶段
当降雨入渗推进速率等于因渗流减小速率时,湿润锋深度达到最大值hmax,此时湿润锋扩展速率dzf/dt=0,结合式(10)得:
(12)
综上所述,降雨条件下边坡湿润锋深度与降雨历时的关系为:
(13)
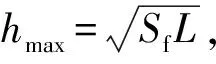
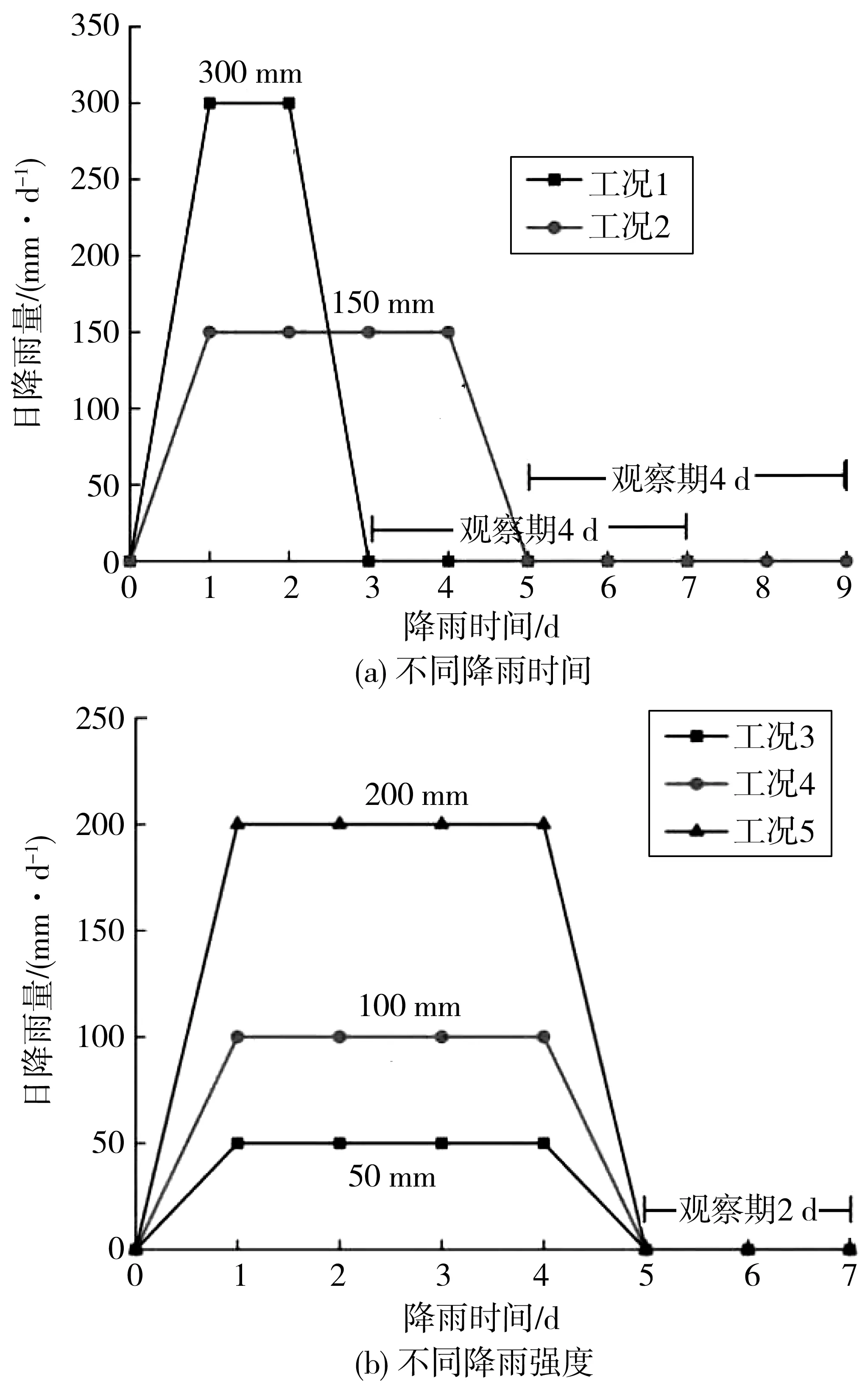
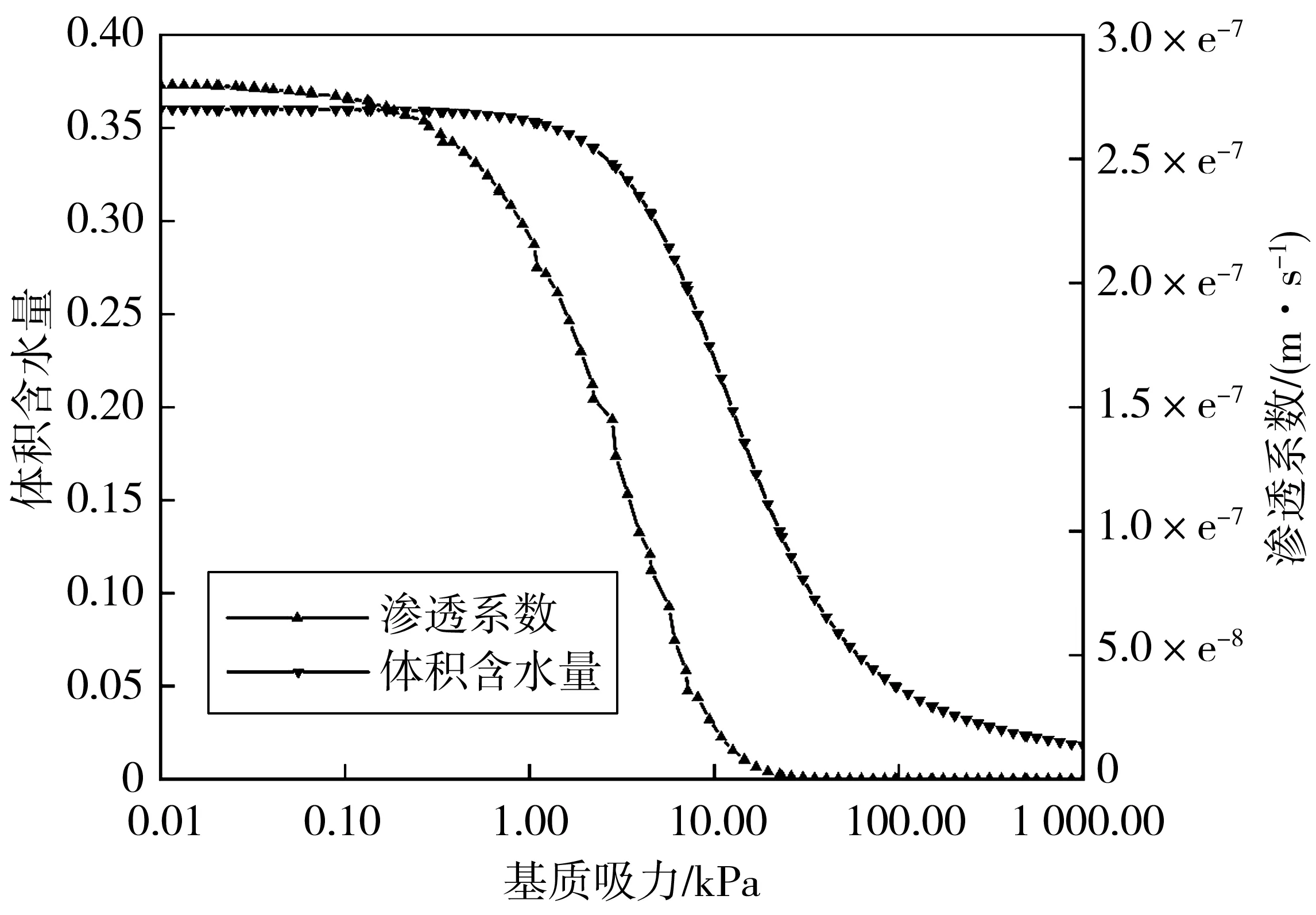
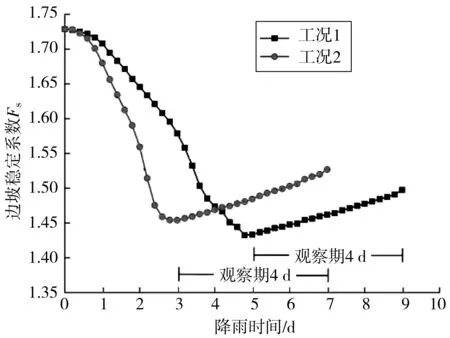
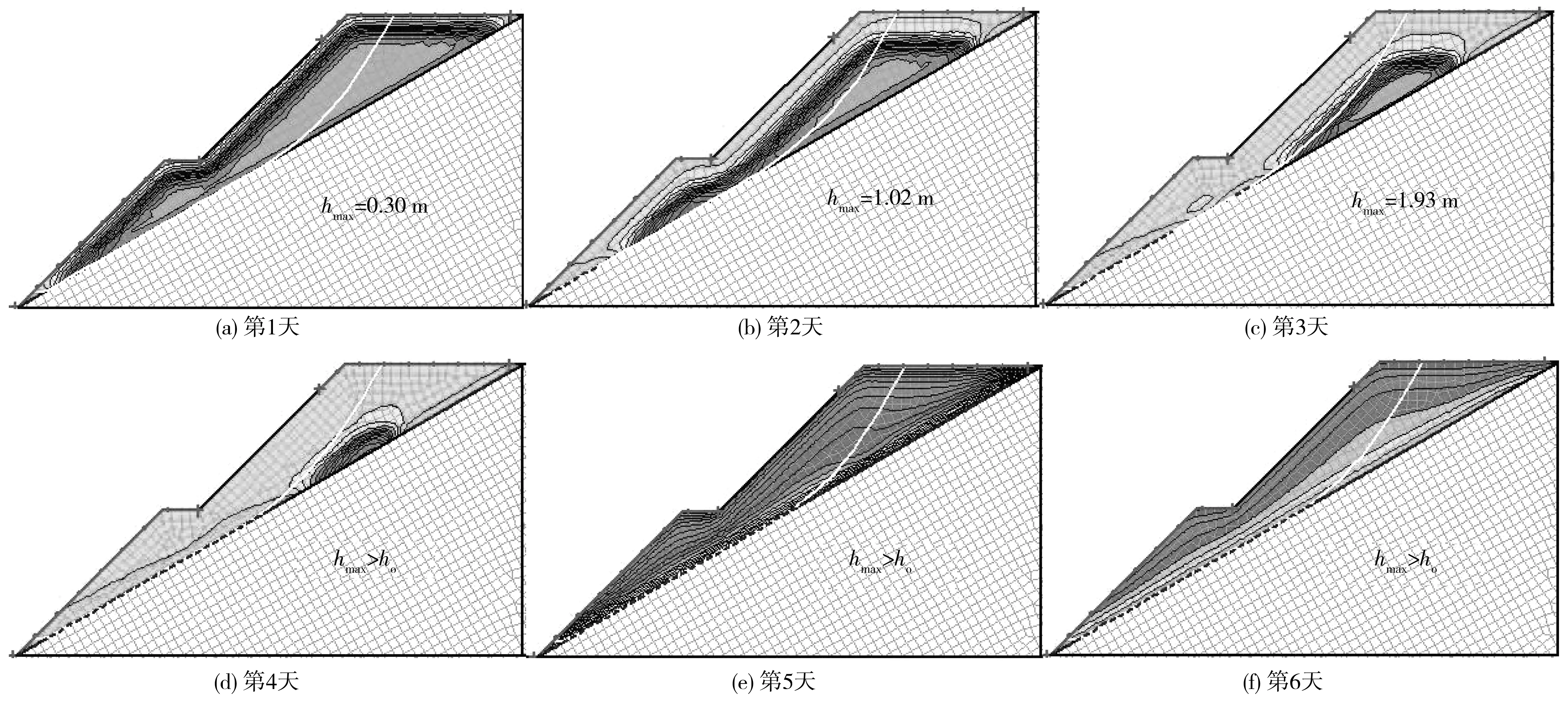
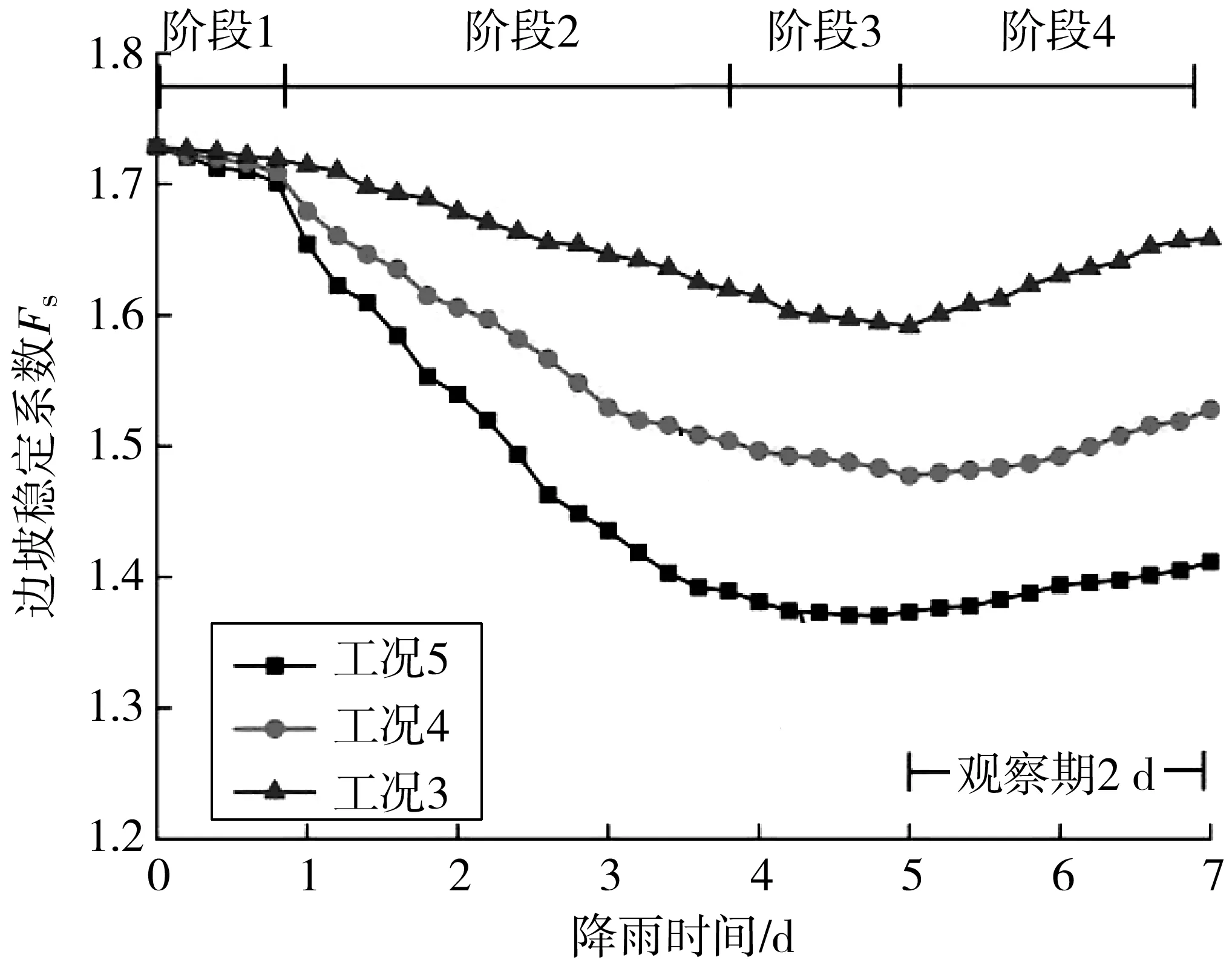
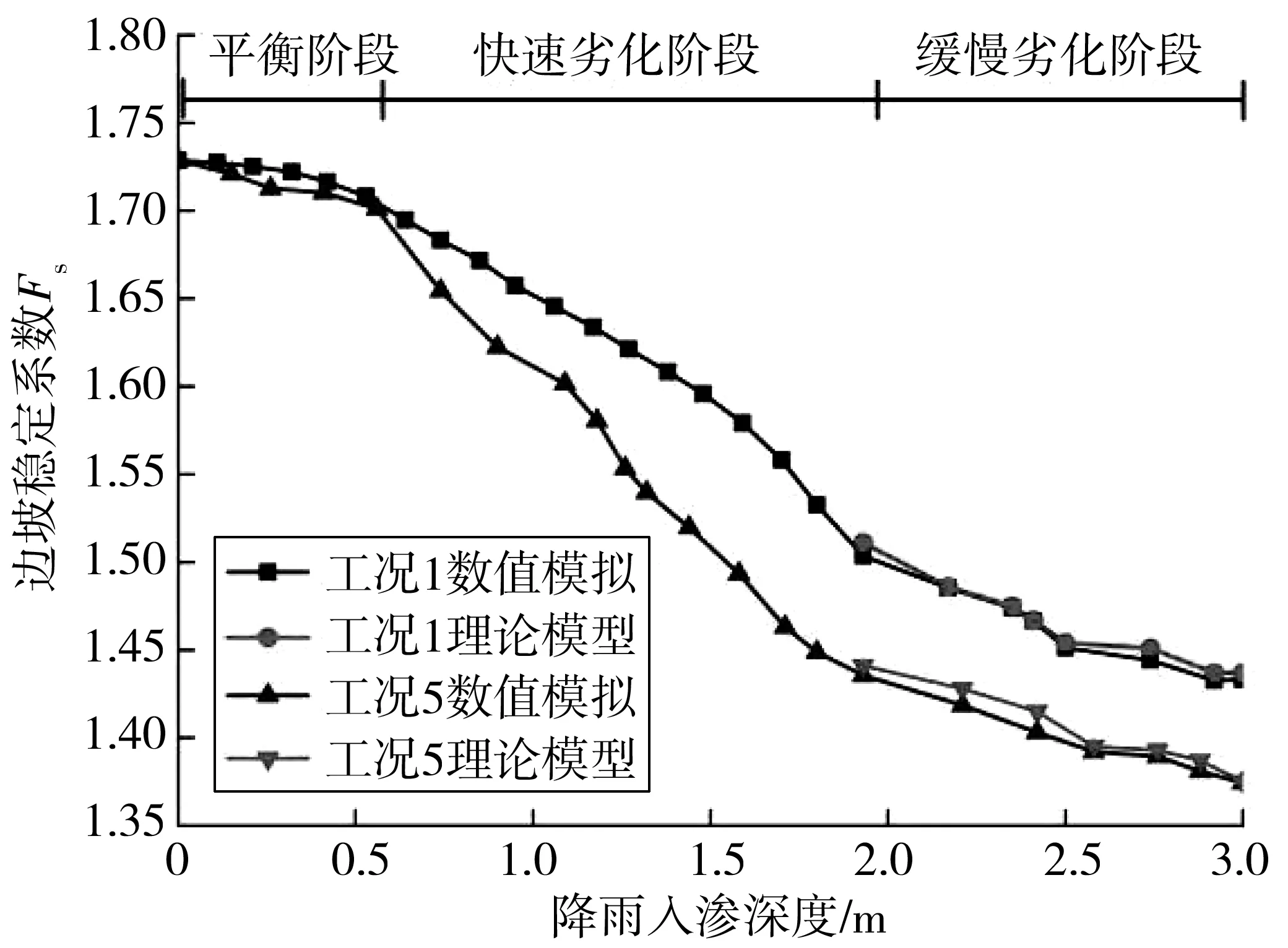
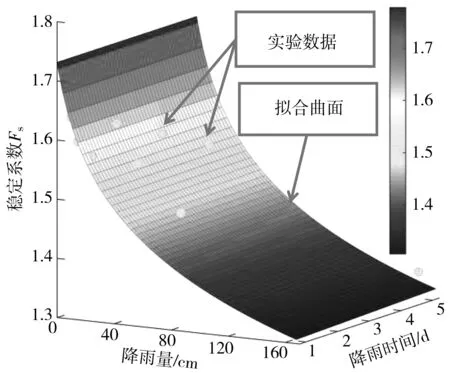
1)hmax 存在某一时刻tmax,当hmax 图3 降雨入渗影响范围及失稳模式(hmax 此时可将该高切坡失稳模式划分为上台阶失稳、下台阶失稳及边坡整体失稳3种。可能失稳滑面分别对应潜在滑面1、潜在滑面2及潜在滑面3,其中上台阶失稳、下台阶失稳模式其稳定性分析同均土质高切坡稳定性分析,即利用式(2)~式(13)进行降雨入渗深度计算及相关稳定性计算;针对边坡整体失稳由于失稳滑面的不确定性,其稳定性计算常见方法为利用有限元软件自动搜索最危险滑面,进而获得高切坡稳定系数。 2)hmax≥h0 存在某一时刻t′max,当hmax≥h0时,其降雨入渗范围及潜在失稳模式见图4。 此时降雨入渗将沿着不透水基岩面流动,结合台阶处雨水垂直入渗,笔者假设条块④、条块⑤整体均处于入渗峰影响范围内,即认为hmax>h1,在稳定性计算过程中需将条块④小三角形OPQ容重考虑成饱和容重,高切坡潜在滑面为湿润锋面及基岩面的双折线型滑面,此假设情况对应强降雨工况。 图4 降雨入渗影响范围(hmax>h0)Fig. 4 Influence range of rainfall infiltration(hmax>h0) 3)hmax=h0 当hmax=h0时,属于hmax≥h0降雨入渗模型的一个特例,其降雨入渗范围见图5。 图5 降雨入渗影响范围(hmax=h0)Fig. 5 Influence range of rainfall infiltration (hmax=h0) 边坡降雨入渗过程是一个复杂的时变过程,该过程中土体含水率及入渗深度随着降雨条件的改变而改变,文献[6]均只建立了降雨临界时刻(无压入渗阶段与有压入渗阶段分界时刻、有压入渗阶段与稳定入渗阶段分界时刻)时的边坡稳定性计算方法,反应降雨型边坡稳定性变化的时变规律较少。未能将降雨入渗过程时变规律与稳定性时变规律分析有效结合起来,且文献[13]在含倾斜基岩面边坡稳定性分析中未考虑饱和土体内由渗流产生的渗透力作用,边坡稳定性计算结果趋于保守,且以湿润锋为潜在滑面时抗滑力计算应采用Fredlund非饱和土体抗剪强度公式求解。基于此,笔者基于不平衡推力系数法建立基岩型台阶状高切坡稳定性与时间变化的关系式,其条块划分及受力情况如图6。 其中条块①抗滑力R1可改进为: (14) 图6 条块划分及受力分析(hmax>h0)Fig. 6 Block division and force analysis diagram (hmax>h0) 下滑力T1可改进为: (15) 条块②计算同条块①,其抗滑力R2为: (16) 下滑力T2为: T2=γsatzfL2tanα2+γwL2zftanα2 (17) 条块③处由于滑面为不透水基岩面,此时基岩面处产生水扬压力,土体抗剪强度应采用MC饱和土体抗剪强度公式求解,则条块③抗滑力R3为: (18) 下滑力T3为: (19) 条块④、条块⑤抗滑力分析同条块③,此时抗滑力R4、R5及下滑力T4、T5分别为: (20) (21) (22) (23) 式中:γsat为土体饱和容重,kN/m3;γw为雨水容重,kN/m3;cn为土体实时黏聚力,kPa;φn为土体实时内摩擦角,(°);ψ0为基质吸力,m;φb为反映基质吸力增加程度的摩擦角,(°);Li为第i块土条滑面长度对应的水平长度,m;α1为上滑面倾角,即土体自稳坡脚,(°),可采用边坡极限稳定坡角确定,即α1=(β+φ)/2,其中φ可取饱和状态下坡体内摩擦角;α2为中滑面倾角,即土体湿润锋与水平面的夹角,(°);α3为基岩面倾角,(°)。 故文中高切坡实时稳定系数为: (24) 式中:λi为条块i剩余下滑力传递给条块i+1的传递系数,按λi=cos(αi-αi+1)-sin(αi-αi+1)tanφi计算,其中i=1, 2, 3, 4,且α3=α4=α5。 将式(14)~式(23)代入式(24)可得当降雨入渗深度hmax≥h0时基岩型台阶状高切坡在降雨入渗过程中的实时稳定系数。 当降雨入渗最大深度hmax=h0时,属于hmax≥h0计算模型的一个特例,此时只需将条块划分模式修改为4块,如图5,计算过程不再赘述。 依据国家气象局规定的降雨量标准[14],重点关注降雨中、降雨后边坡性质变化规律,摒除小雨~中雨降雨工况下高切坡稳定性变化微弱的情况,选取暴雨、大暴雨及特大暴雨3种降雨强度,其中暴雨取50、100 mm/d、大暴雨取150、200 mm/d、特大暴雨取300 mm/d共5种工况进行计算。 已有研究多针对降雨过程中边坡内部渗流场及稳定性分析,考虑雨后边坡内部渗流场及稳定性变化的研究较少,基于此,考虑高切坡失稳破坏在降雨作用下的滞后性,通过建立典型砂土覆盖层基岩型台阶状高切坡算例模型,分别固定降雨总量及降雨时间拟定典型降雨工况,以揭示各降雨工况下高切坡降雨入渗过程及降雨后内部渗流场及稳定性变化规律,如图7。 图7 各工况雨型函数Fig. 7 Rain-type functions under various working conditions 笔者利用Geo-studio数值模拟软件建立前述砂土覆盖层基岩型台阶状高切坡数值模型,开展多工况下边坡降雨入渗过程研究。 3.3.1 模型建立 高切坡模型尺寸见图8,其中模型底部边界设定为竖直约束和水平约束边界;左右边界为水平约束边界;高切坡坡表和坡脚路面设置为降雨入渗及潜在的排水边界,为考虑雨后高切坡稳定性回升,同时还将高切坡坡表设置为蒸发辐射边界,笔者将研究工点定位于三峡库区及川渝地区,尤以四川盆地阴天、雾天较多,造成日照时间短、强度弱,全年平均太阳辐射总量约9 150~11 480 kJ/d/m2,夏季虽多雨但光照较强,笔者将高切坡表面辐射值设为10 000 kJ/d/m2;模型两侧边界及底部设定为不透水边界。 考虑计算精度与计算时步,将模型划分为4 638个节点和4 492个单元,渗流计算过程中,根据所拟定降雨工况分别设置35个及45个时间步,每个时间步时长约4.8 h,共计7、9 d,每个时间步最大迭代次数为50步,迭代误差小于1%视为收敛。 坡体参数取值如表1。 表1 砂土及不透水基岩物理力学参数Table 1 Physical and mechanical parameters of sand and impervious bedrock 图8 高切坡有限元模型尺寸(单位:m)Fig. 8 Dimensional drawing of high-cut slope finite element model 模型边坡坡体为均质非饱和砂土,其渗透系数为基质力的函数,而非常数,即基质力随含水量的变化而变化。土体非饱和特性参数如表2,笔者利用Geo-studio数值模拟软件内置的非饱和砂土样本函数,及实验所测砂土饱和含水率及残余含水率生成砂土覆盖层土水特征曲线及渗透系数函数,见图9。 图9 砂土土水特征曲线渗透系数函数Fig. 9 Permeability coefficient function of sand soil-water characteristic curve 3.3.2 稳定性计算与分析 图10 工况1高切坡湿润锋变化Fig. 10 Variation diagram of wetting peak of high-cut slope in working condition 1 图11 工况2高切坡入渗峰变化Fig. 11 Variation diagram of infiltration peak of high-cut slope in working condition 2 图12 相同降雨总量条件下高切坡稳定系数时程曲线Fig. 12 Time-history curve of stability coefficient of high-cut slope under the same total rainfall 图12为工况1及工况2高切坡稳定系数Geo-studio数值模拟结果,可见,两条曲线均呈先下降后上升态势,工况1高切坡稳定系数衰减斜率小于工况2,当降雨时间同为3 d时,工况2高切坡稳定系数累计减小幅度约比工况1大0.125,表明高切坡稳定性与降雨时间成负相关,降雨时间一致时,降雨强度越大,边坡稳定性劣化越剧烈;当降雨总量一致时,工况1导致高切坡稳定系数累计降低幅度约比工况2大0.021,表明降雨总量一致时,与降雨强度相比,降雨时间影响边坡稳定性较剧烈,即在边坡稳定性长期监测中应更加注意长时小雨对边坡稳定性造成的影响。降雨结束后观察期内工况1、工况2高切坡稳定系数均有缓慢回升现象,观察期内工况1累计回升0.065,回升幅度为4.5%;观察期内工况2累计回升0.073,回升幅度为5.0%,表明降雨期间工况1导致高切坡稳定系数下降幅度较大,且降雨结束后高切坡稳定系数回升幅度较小。究其原因在于:笔者在设置模型降雨边界条件时改善了常规的降雨入渗边界,不仅考虑雨后雨水缓慢出渗,还充分考虑了雨后蒸发现象,使得高切坡稳定系数雨后出现回升现象,孔隙水压力消散加速,土体有效应力提高,这也更加符合事实,降雨结束后工况1入渗深度较工况2大,土体骨架颗粒的存在使得单位时间内工况1雨水出渗速度较工况2小,滞留高切坡孔隙水较多,因此稳定系数回升速度慢,相同观察期内稳定系数回升幅度较工况2小。 笔者通过拟定降雨工况3 、工况4及工况5揭示了砂土覆盖层基岩型台阶状高切坡坡体内部渗流场在相同时间不同降雨强度条件下的变化情况,篇幅限制,笔者仅给出工况5降雨入渗演化过程,见图13。工况3及工况4的结果反应在图14中。 图13 工况5降雨时间内高切坡入渗峰变化Fig. 13 Variation diagram of infiltration peak of high-cut slope during rainfall in working condition 5 图14 相同降雨时间内高切坡稳定系数随降雨强度变化Fig. 14 Variation diagram of stability coefficient of high-cut slope changing with rainfall intensity in the same rainfall time 图14为工况3、工况4及工况5高切坡稳定系数演化过程,可见,降雨强度一定时,随着降雨时间的增大,边坡稳定性逐渐劣化,工况3、工况4及工况5导致高切坡稳定系数分别累计下降0.137、0.251、0.358,表明相同降雨时间内高切坡稳定性劣化程度与降雨强度成正相关,究其原因在于相同时间内降雨强度越大,降雨总量即越大,覆盖层坡体饱和度、孔隙水压力、饱和区域越大,降雨入渗越严重,边坡稳定性下降越剧烈,因此,特定边坡在其降雨历史过程中应注意暴雨-特大暴雨工况对边坡稳定性的影响。降雨结束后相同观察期内3种工况稳定系数均有回升,其中工况3、工况4及工况5稳定系数分别回升0.067、0.051、0.041,回升幅度分别为4.2%、3.4%、3.0%,可见工况3回升幅度最大,工况4次之,工况5最小,究其原因在于工况3降雨入渗总量最小,雨后孔压水压力消散最快,边坡排水过程较快,高切坡稳定性恢复最快,相同观察期内边坡稳定系数回升幅度最大。从降雨周期内看,高切坡稳定系数劣化时程曲线可划分为4个阶段,阶段1为平稳阶段,该阶段内边坡入渗深度较小,本例中为0~0.5 m,边坡稳定系数变化幅度小;阶段2为快速劣化阶段,该阶段内边坡入渗深度逐渐增大,本例中为0.5~2 m,边坡稳定系数劣化速率最快,稳定系数变化幅度最大;阶段3为缓慢劣化阶段,该阶段内边坡入渗深度继续增大,本例中为2~3 m,边坡稳定系数劣化速率较小,稳定系数变化幅度较小;阶段4为回升阶段,该阶段内由于蒸发作用,边坡稳定系数逐渐回升。 通过计算工况1及工况5不同入渗深度的高切坡稳定性,其中当降雨入渗深度zf 图15 高切坡稳定系数随降雨入渗深度变化曲线Fig. 15 Variation curve of high-cut slope stability coefficient changing with rainfall infiltration depth 综上所述,对于某一特定边坡,决定边坡稳定性的主要因素为降雨时间及降雨强度,基于此可获得特定砂土覆盖层基岩型台阶状高切坡在不同降雨时间及降雨强度作用后的稳定性情况,利用MATLAB 2016 a数据分析软件对模拟数据进行拟合,其中为更准确的描述降雨强度q随时间的变化趋势,仍采用典型雨型函数并用降雨总量刻画降雨时间T内的降雨强度,可发现,边坡降雨实时稳定系数Fs与降雨总量Q、降雨时间T满足如下二元函数关系: Fs=F0[1-Ae-BTln(0.1Q+1)] (25) 式中:F0为边坡初始稳定系数;Q为降雨总量,cm;T为降雨时间,d;A、B为MATLAB拟合参数,经拟合完成的曲面三维图形如图16,其中A=0.085 3,B=0.004 5,可见,对于笔者所建砂土覆盖层基岩型台阶状高切坡,认定其稳定系数Fs与降雨总量Q、降雨时间T满足式(25)的函数关系是合理的。 图16 高切坡稳定系数与降雨强度及降雨时间的关系Fig. 16 Relationship between high-cut slope stability coefficient and rainfall intensity and rainfall time 以降雨型砂土覆盖层基岩型台阶状高切坡为研究对象,通过建立该类高切坡理论模型及数值模型,建立了其稳定性计算方法,利用Geo-studio数值模拟手段揭示了其在不同降雨工况下的降雨入渗过程及稳定性演化过程,并给出了该类型降雨高切坡的稳定性预测方法,主要结论如下: 1)针对无限长边坡降雨湿润锋计算忽略了有限长边坡尺寸效应,建立了两级台阶砂土覆盖层基岩型高切坡理论模型,假定潜在滑面为湿润锋面及基岩面的双折线型滑面,基于不平衡推力系数法建立了降雨入渗下砂土覆盖层基岩型台阶状高切坡稳定性计算方法。 2)利用Geo-studio数值模拟软件建立了砂土覆盖层基岩型台阶状高切坡数值模型,开展了多工况下高切坡降雨入渗过程研究,发现高切坡稳定性状态与降雨时间、降雨强度成负相关,降雨总量一致时,与降雨强度相比,降雨时间影响边坡稳定性较剧烈;降雨入渗深度及总量越大,高切坡雨后稳定系数回升幅度越小;同时将高切坡稳定系数劣化过程划分为平稳阶段、快速劣化阶段、缓慢劣化阶段及回升阶段共4个阶段。 3)获得了特定砂土覆盖层基岩型台阶状高切坡在不同降雨时间及降雨强度作用后的稳定性情况,基于此给出了该类高切坡在不同降雨量及降雨时间下的稳定性预测方法。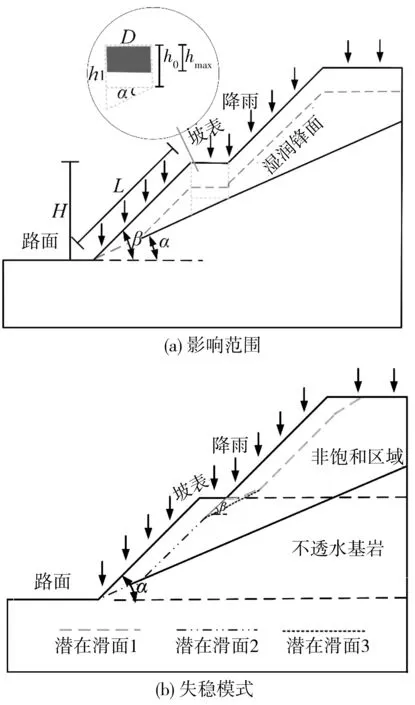
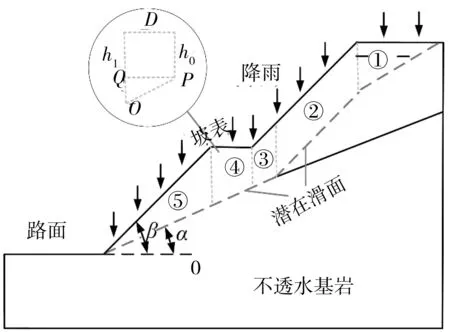
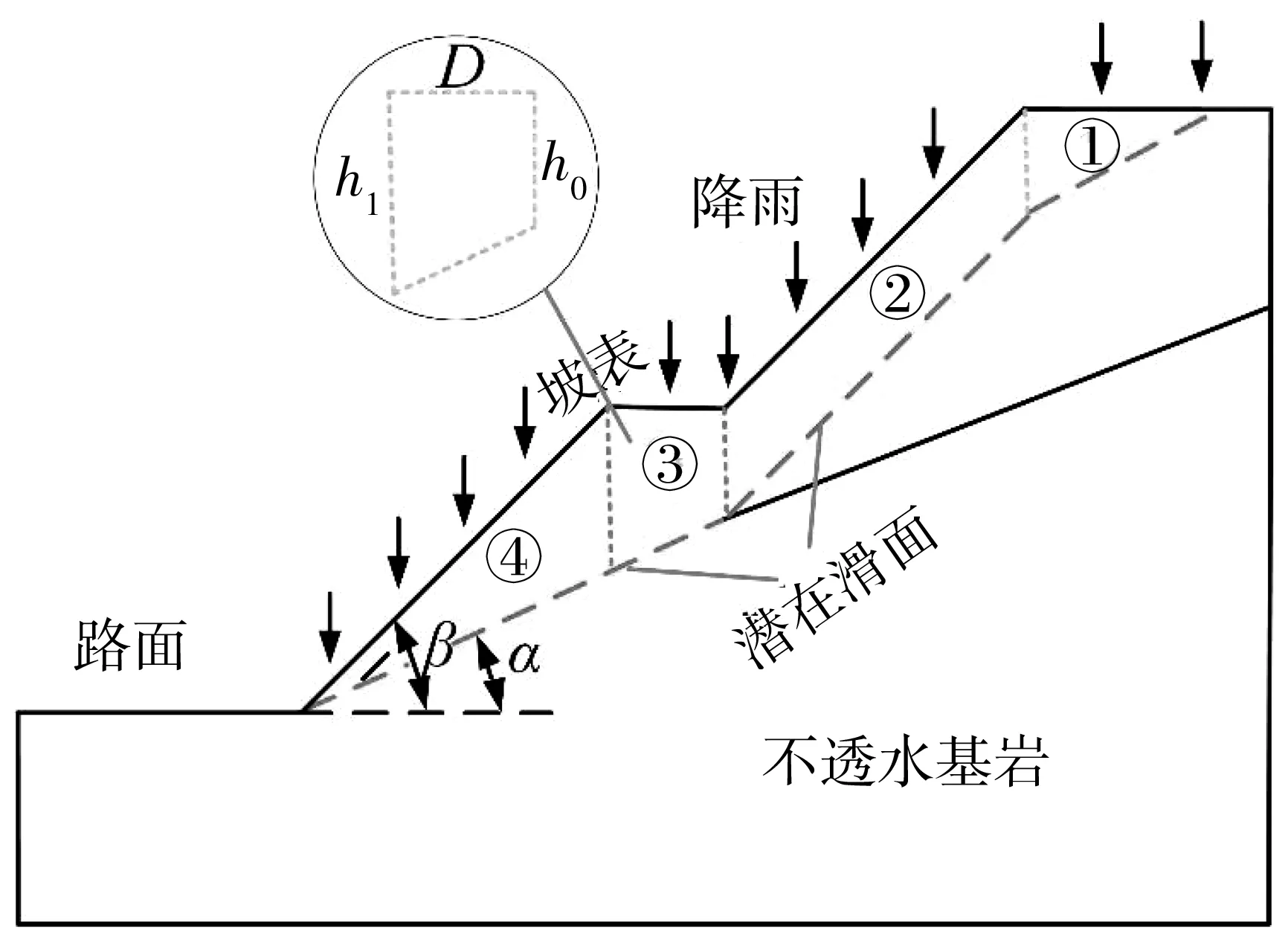
2 稳定性计算
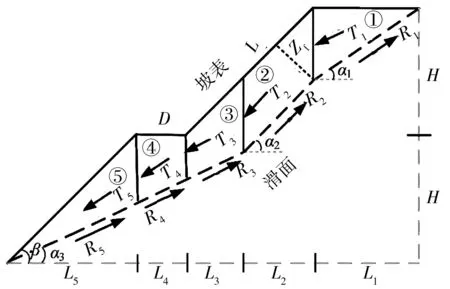
3 算例分析
3.1 降雨强度工况选取
3.2 降雨类型及降雨时间工况选取
3.3 Geo-studio数值模拟


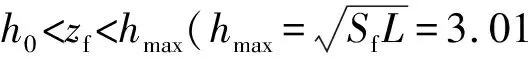


4 结 论
