基于机器学习的多元化合物带隙预测

董延华，佘安琪，王 铭，梁久欣，孙宏宇

(吉林师范大学 计算机学院，吉林 四平 136000)

0 引言

近年来，对化学空间的高通量探索极大地帮助了合理的材料设计和发现.目前已有大量材料性能(包括电子结构、热力学和结构性能)的开放数据库.机器学习统计技术正逐渐进入材料科学领域[1]，基于机器学习的方法对材料在明确定义的化学空间内进行预测的有效途径是对目标化学空间内的新化合物进行预测[2].通过机器学习来预测材料性质的例子包括预测分子和周期系统的性质、过渡态、电势、结构分类、介电性质和能带隙的预测[3].二维材料是由一个或多个不垂直排列和周期性的原子层组成的晶体材料，具有许多独特的物理和化学特性.与三维材料的结构相比，二维材料的化学和结构修饰的可能性使其成为材料科学的主要研究对象[4].二维材料主要由石墨烯，单元素的硅烯、锗烯、锡烯、硼烯、黑磷，过渡金属硫族化合物(MoS2、WSe2等)，主族金属硫族化合物(SnS、SnS2等)以及h-BN、Bi2O2Se等组成[5-7].多元化合物在催化、电池等方面都有广泛的应用，相较于石墨烯而言，多元化合物组分和结构的多样性，使其具有许多物理和化学特性[7-8].

带隙是绝缘体和半导体中价带顶部和导带底部之间的电子伏特能量差，是电子脱离束缚态所需的最小能量[9].计算带隙的实验需要大型且昂贵的设备，十分烦琐，有些材料需要特殊的环境处理，因此，精确计算带隙仍然是固体物理中尚未解决的问题之一[10].随着计算机技术的不断发展，第一性原理计算带隙成为研究人员取得带隙值的主要方式.大部分电子结构都是基于密度泛函理论(Density Functional Theory，DFT)计算得到的Kohn-Sham带隙，由于计算理论局限性，DFT计算得到的带隙往往小于真实值.常常使用基于多体扰动理论的GW方法来获得更真实的带隙，但计算高精度的G0W0耗时长，所需计算资源多，同时计算的体系原子数较少，因此，需要探索一种计算成本低并且较为准确估计带隙的方法[11].预测一种新材料的带隙介于DFT计算结果和真实值之间，将使研究人员在寻求更复杂的带隙计算方法之前，对实验的预期有一个很好的了解.

本工作采用2D Materials Encyclopedia数据库[12]中基于第一性原理和密度泛函理论计算的多元化合物数据集，提取多元化合物的总能量、带隙，并加入原子电负性、第一电离能和原子的有效原子半径等性质，来预测更为精确的带隙[13].将原始数据集随机分为训练集和测试集，分别选用岭回归和Lasso回归、支持向量回归(SVR)、随机森林机器学习方法对数据进行训练[14-16]，采用交叉验证的方法建立带隙的预测模型.最后，利用所得模型对测试集进行预测，并对预测结果进行评估.这种方法在第一性原理计算已经能够减少实验时间的基础上，进一步提高研究效率并降低研究成本.

2 实验

2.1 机器学习原理与方法

本研究采用的方法有岭回归和Lasso回归、随机森林、支持向量回归(SVR).图1简要总结了几种算法并显示了算法之间的联系.

图1 总体工作流程

2.1.1 岭回归和Lasso回归

线性回归是预测建模中最常用的统计方法.岭回归和Lasso回归是两种带有正则化项的线性回归[17]，用于防止过度拟合和降低模型复杂性.在岭回归中，通过L2范数作为惩罚来修改代价函数，如果系数大，代价函数就会受到惩罚.这意味着岭回归缩小系数，有助于克服多重共线性.具体为

(1)

类似地，Lasso回归将系数的大小(L1范数)作为一种惩罚，而不是取系数的平方.这种类型的正则化可能会导致一些系数恰好为零，也就是说，一些特征在评估输出时完全被忽略了.因此，Lasso回归不仅有助于减少过拟合，而且有助于特征选择.具体为

(2)

在公式(1)和(2)中：X表示输入特征的矩阵；y是实际带隙值；λ1和λ2是调谐参数.

2.1.2 支持向量回归

支持向量回归(SVR)与支持向量机(SVM，一种分类算法)不同，可用于预测连续变量[18].与其他旨在减少真实值和预测值之间差异的线性回归模型不同，SVR试图在预定义的阈值ε内匹配最佳超平面，在不违反边界的情况下，拟合尽可能多的数据点，如图2所示.错误阈值控制边界的宽度.目标函数和约束可表示为

(3)

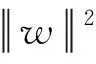
2.1.3 随机森林

决策树通过不断地将训练样本划分为分支进行分层学习，从而使每次分割的信息增益最大化.这种分支结构允许决策树学习非线性关系.随机森林是一种集成方法[18]，它将分类决策树拟合到数据集的子集上，并对树进行平均，以提高预测精度和减少过拟合.在模型训练过程中，每棵树的样本都是用替换来绘制的，这意味着一些样本可能会在一棵树中被多次使用.替换抽样降低了模型的方差，但不以增加偏差为代价.当拆分树中的节点时，使用特征的随机子集来创建最佳拆分.由多棵决策树组合形成的模型中：{h(x，θt)，t=1，2，…，T}是服从独立分布的随机变量，x为自变量，T为决策子树的个数.

图2 支持向量回归

分类模型预测结果为

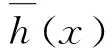
2.2 数据处理与模型建立

使用机器学习方法进行带隙预测的过程中，研究对象及其数据的选取尤为重要.为了建立可靠的二维材料数据集，本文选取了主族金属元素、过渡金属元素、氧族与卤族元素组成的多元化合物二维材料为研究对象，这样共得到5 000多种化合物，选择其中具有一定带隙的3 244种化合物进行研究.模型的输入被称为特征或描述符，通过实验和简单的计算获得，图3显示了原子占比，电负性差异以及原子量和带隙的关系.应用的机器学习模型仅根据组成元素的元素属性使用特征集来预测能带隙.由于目前还没有一种简单有效的方法来描述晶体结构，因此在机器学习模型中，特征集仅限于组成特征.同时发现精确的原子结构可能并不需要达到一定的预测精度.

图3 带隙与三种特征的关系

机器学习预测带隙的过程：

(1)数据准备 将3 244组数据的数据集随机分成2 900组数据组成的训练集和344条数据构成的测试集.

(2)模型训练 设置10折交叉验证，分别建立Lasso、SVR和随机森林算法模型，利用3种模型对训练集的G0W0带隙进行训练.

(3)模型性能评估 使用MAE评价指标对模型效果进行评估.

(4)模型应用 利用训练后的多个算法模型对测试集的带隙进行独立预测，并简单评估.

3 结果与讨论

数据集随机分成训练集和测试集，比例为9∶1.对于每种方法，在训练集上执行10次交叉验证，以优化模型的超参数，然后报告测试集上的平均绝对误差(MAE)和均方误差(MSE).公式为：

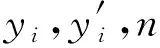
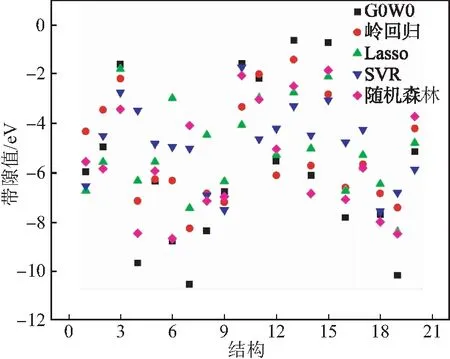
图4 预测结果比较Fig.4 Comparison of prediction results

表1给出了使用相同特征的不同机器学习方法的带隙预测的MAE、MSE分数.从表1可以得出，随机森林算法的平均绝对误差为1.096eV且均方误差值为2.087 eV，Lasso为典型的广义线性回归模型，而其余模型均为非线性的复杂模型.由此也可以看出，该多元化合物数据集中的属性特征与目标变量带隙之间有着复杂的非线性关系的特点.其中，对于Lasso模型，参数alpha与max_iter分别代表模型的惩罚项大小和模型训练的迭代次数.对于SVR模型，参数kernel、C、gamma与epsilon分别代表核函数类型、惩罚项大小、核函数参数和距离误差.对于随机森林模型，参数estimators代表了使用到的基本树模型的数量.

表1 不同机器学习方法的带隙预测的MAE、MSE分数

表2是测试集通过不同的机器学习方法预测带隙与真实值的比较.从表2数据可以看出，在多元化合物带隙极小(≤-8.0 eV)或极大(≥-3.0 eV)的情况下进行4种模型的预测，得到的预测带隙误差较大，但在带隙数值合理的范围(-7.0 eV≤G0W0≤-4.0 eV)内，预测值与真实值非常接近，误差在0.5 eV范围内.在选取模型时，基于线性岭回归模型和Lasso模型预测得到的带隙数值相较其他而言比较接近，而且由于采用了线性回归的方法，算法的复杂度并不高，更能提高今后更大数据量研究的计算效率.而由图4可以看出，结合测试集预测结果的对比与误差分析，虽然在少数情况下SVR的预测精度较高，但在大多数情况下随机森林的预测精度更好，而造成这种结果的原因是随机森林有许多调整参数，构建独立的决策树，并对每个决策树的带隙预测进行平均.

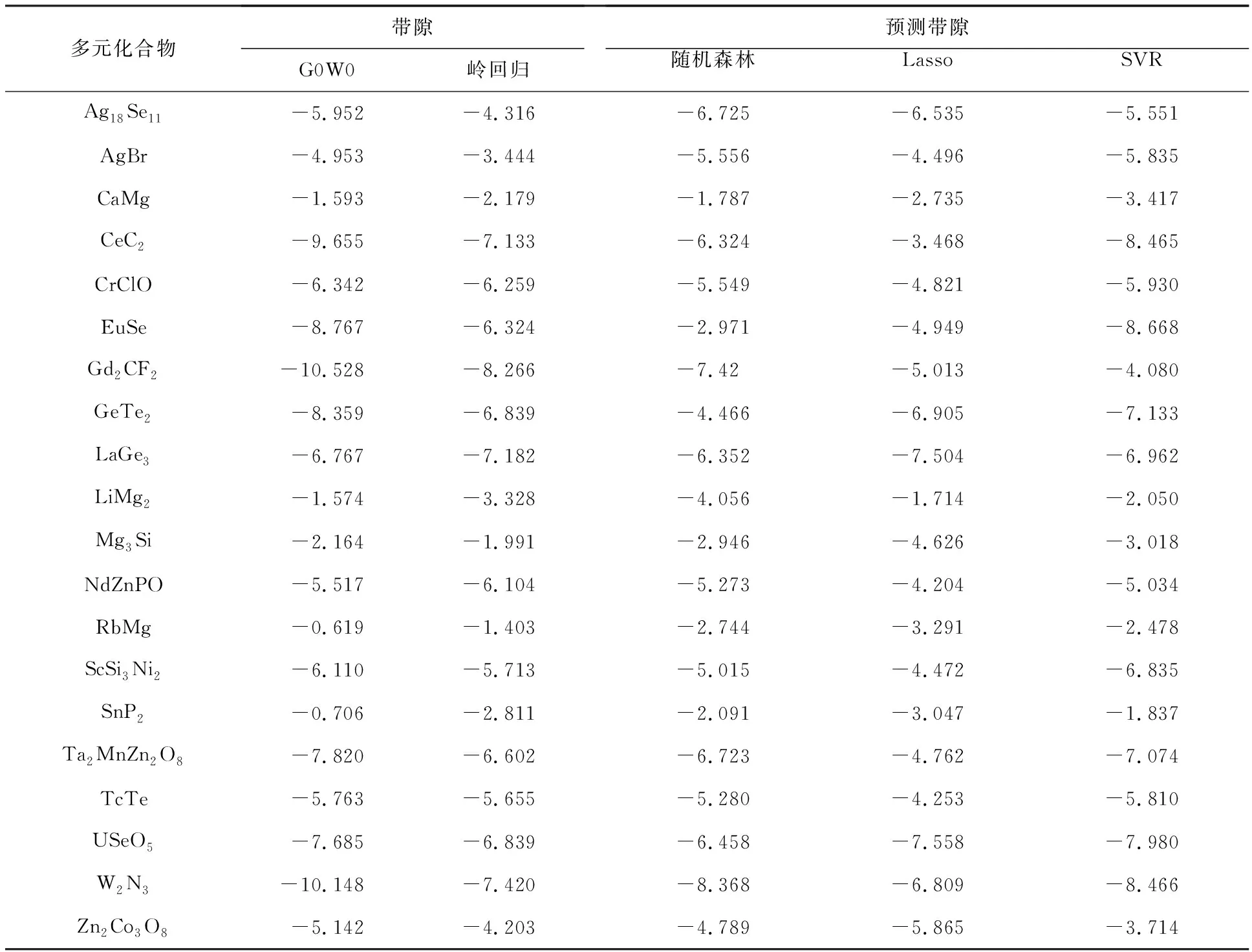
表2 测试集预测带隙的比较

4 结语

随着数据科学和高效的机器学习工具的不断发展，机器学习已经在不同领域用于解决某些特定的问题，为材料科学中许多尚未解决的问题提供了一个独特的思路.本文提出了几个机器学习方案训练并预测带隙，所选取的多元化合物带隙值约为-11～0 eV，基于机器学习方法，训练可以预测带隙值的模型.结果表明，使用仅基于成分信息的特征集，能够进行带隙预测并且具有合理的准确性.本工作讨论的模型中，运用随机森林算法建立的模型具有最佳性能，MAE和MSE分别是1.096 eV和2.087 eV，而SVR算法在多元化合物带隙的预测中也表现出较好的效果.与第一性原理方法相比，这些机器学习方法可以在显著降低计算成本的情况下可靠地预测带隙.由此可见，基于机器学习预测多元化合物带隙的方法是可行的.进一步改进模型的两个主要方向是增加更多的训练数据和使用特征工程，将材料晶体结构加入到特征集中，具有进一步提高预测精度的潜力.