基于区间Ⅰ型删失数据的切片逆回归

董小刚，赵立妍，刘新蕊，王纯杰

(长春工业大学 数学与统计学院，吉林 长春 130012)

0 引言

在医学、生物学、可靠性工程学、公共卫生学、保险精算学以及人口统计学等学科的研究中，常常无法观测到研究个体的准确失效时间，只知道它发生在观测时间之前还是之后，即为区间Ⅰ型删失数据[1].在生存问题中，若对众多协变量直接进行处理，可能会导致“维数灾难”问题，因此对变量进行降维是十分必要的.近年来，Lasso[2-3]和SCAD[4]等变量选择方法应用广泛.然而这些方法需要在特定模型下进行考虑，具有一定的局限性.1991年，K.C.Li[5]提出了切片逆回归(Sliced Inverse Regression，SIR)这一非参数降维方法，该方法不需要对模型进行假设，且具有容易实施的特点；在此基础上，R.D.Cook[6]、B.Li和S.Wang[7]提出了SIR的改进方法；T.Hsing和R.J.Carroll[8]、L.Zhu和K.Ng[9]研究了SIR方法在不同切片范围下其估计量的性质；1999年K.C.Li[10]提出了双切片逆回归的方法，并首次将SIR方法推广至删失数据的分析中；此后，W.Lu和L.Li[11]对右删失数据进行线性无偏变换，然后运用SIR方法进行降维；M.Shevlyakova[12]通过对删失数据赋予相同的权重，将SIR方法运用于右删失数据中；J.K.Yoo[13]采取了两种右删失数据变换方法对SIR方法进行了改进.在现有研究中，很多都是右删失数据下的SIR方法，然而关于区间Ⅰ型删失数据下SIR方法的研究较少，因此将SIR方法推广到区间Ⅰ型删失数据中十分必要.

本文根据区间Ⅰ型删失数据的特点，采用了3种不同的切片方式：构造权重矩阵、改进SIR方法以及对协变量进行充分降维，在模拟研究中验证该方法的有效性，并将其运用于实例分析中.

1 区间Ⅰ型删失数据下的切片逆回归

区间Ⅰ型删失的观测值可以表示为

Di={Ci，δi，Xi}，i=1，2，…，n.

其中：Ci为观测时间；δi=I(Ti≤Ci)；Ti为生存时间；Xi为与生存时间有关的p维协变量.

SIR是一种经典的充分降维方法，也可以对变量进行选择.降维模型为

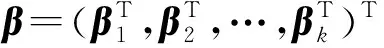
当满足这个条件时，逆回归曲线落在由有效降维方向决定的降维子空间内[4].

1.1 权重矩阵

根据区间Ⅰ型删失数据特点，考虑了3种切片方式：方式1对δi=1(i=1，2，…，n)，即左删失的个体进行切片，将其观测时间范围切成S个不重叠的区间；方式2将δi=0(i=1，2，…，n)，即右删失个体的观测时间切为S个不重叠的区间；方式3将所有的观测时间Ci(i=1，2，…，n)切成S个不重叠的区间.

当第i个个体落入第s(s=1，2，…，S)个切片内时，若δi=1，即个体左删失，则认为个体感兴趣事件在时刻Ci之前是等可能发生的；若δi=0，即个体右删失，则认为个体感兴趣事件在时刻Ci之后是等可能发生的，由此给出权重矩阵.例如，考虑7个观测数据(见表1).

表1 观测数据

选择切片个数S=4，方法1的切片区间为(0，7]，(7，10]，(10，15]，(15，∞)；方法2为(0，8]，(8，12]，(12，14]，(14，∞)；方法3为(0，7]，(7，10]，(10，14]，(14，∞).3种方法对应的权重矩阵如表2—4所示.

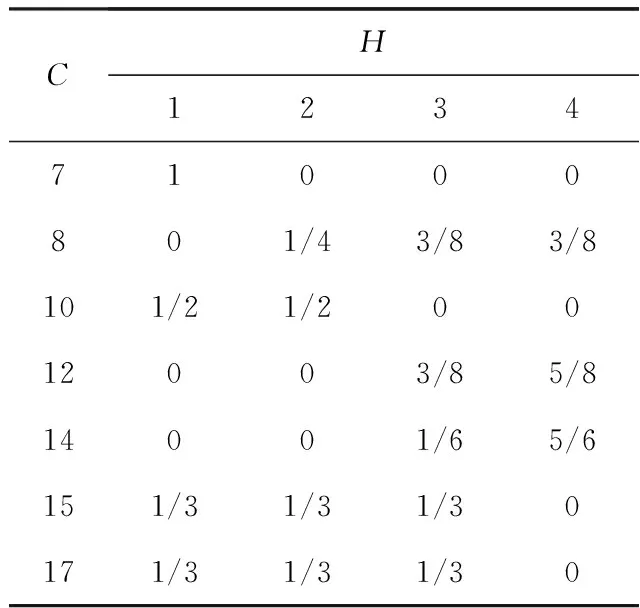
表2 方法1权重矩阵

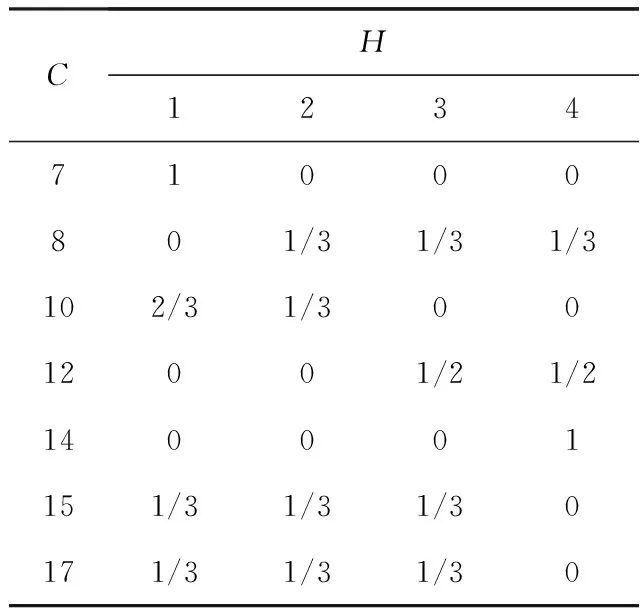
表3 方法2权重矩阵

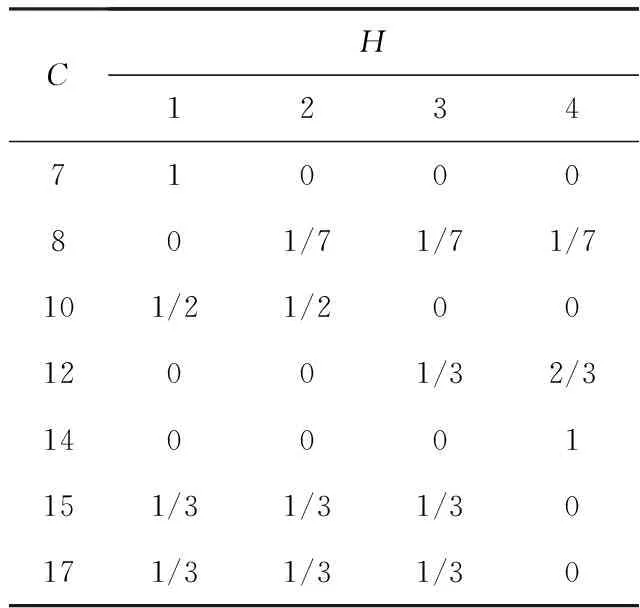
表4 方法3权重矩阵

分别运用以上3种不同的方法进行切片，但计算权重矩阵的思想是相同的.以方法1权重矩阵为例.当个体左删失时，如观测时间点10落在第二个切片内，其感兴趣事件等可能发生在前两个切片内；当个体右删失时，如观测时间点12落在第三个切片2/5处，该切片后面3/5和第四切片内感兴趣事件均可能发生，则第三个切片的权重为3/8，第四切片的权重为5/8.其他的同理.

1.2 算法步骤

根据上述权重矩阵来改进切片逆回归，算法步骤为：

(1)将X=(X1，X2，…，Xn)T标准化为Z，即

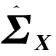
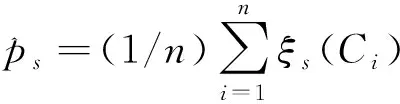
(3)计算每个切片内Z的样本均值

其中W为权重矩阵；

(4)构建加权协方差矩阵

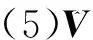
(6)将其转化回原来的尺度

1.3 中心降维子空间维数确定

在充分降维的过程中，确定中心降维子空间的维数K十分重要，直接影响了降维结果.为此，1991年，K.C.Li[4]提出了一个χ2检验来确定维数K.

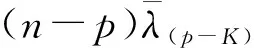
根据p值可以确认SIR中心降维子空间的维数.当K=k时，根据上述公式计算对应的p值，若得到的p值小于显著水平α，则拒绝原假设，即维数大于k，应继续进行检验，直到所计算的p值大于α，即接受原假设.此时对应的k值即为降维维数.

2 模拟研究

为了验证所提方法的有效性，考虑使用SIR来对区间Ⅰ型删失数据下的加速失效模型(AFT)进行模拟研究.令

Y=ln(T)=βTX+ε.

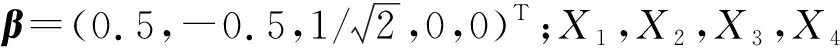
依据中心降维空间的估计值与真实值之间多元相关系数的平方(R2)来判断降维模型的好坏：

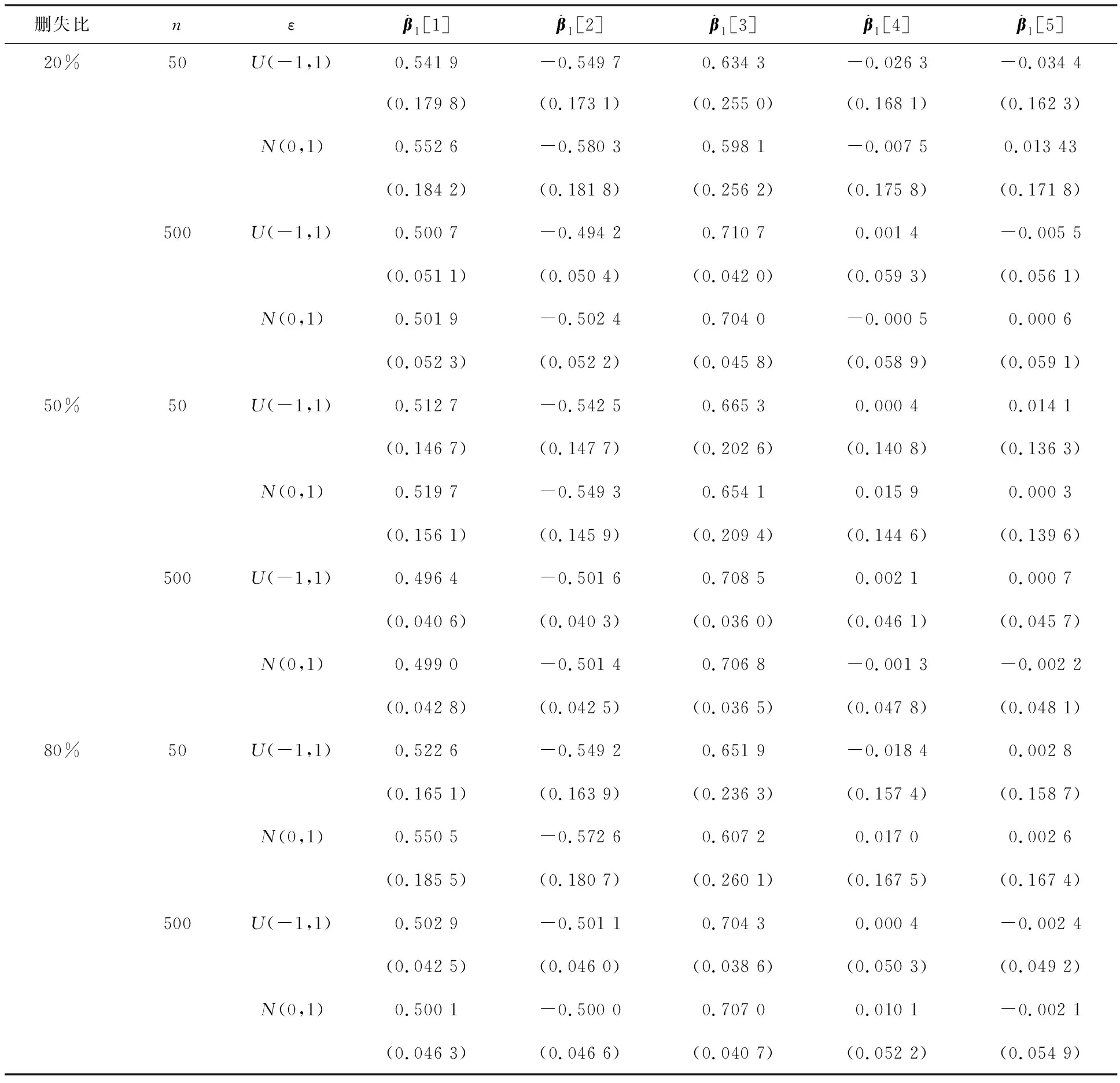
表5 方法1的SIR估计和标准差

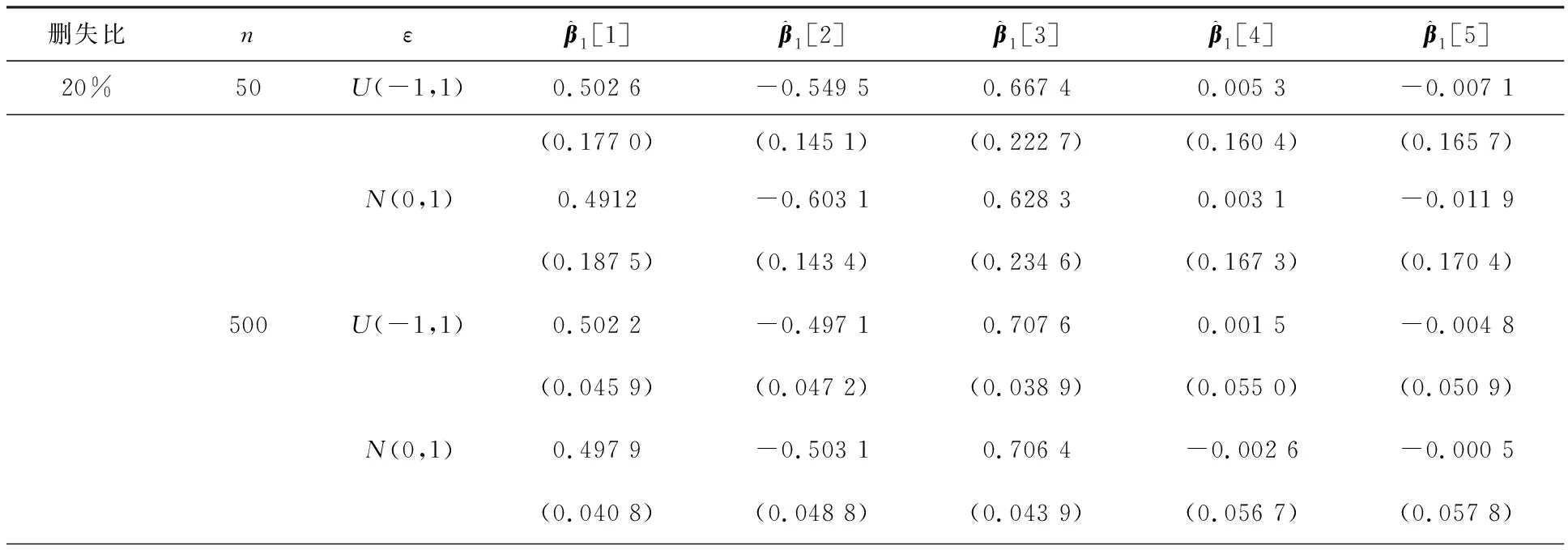
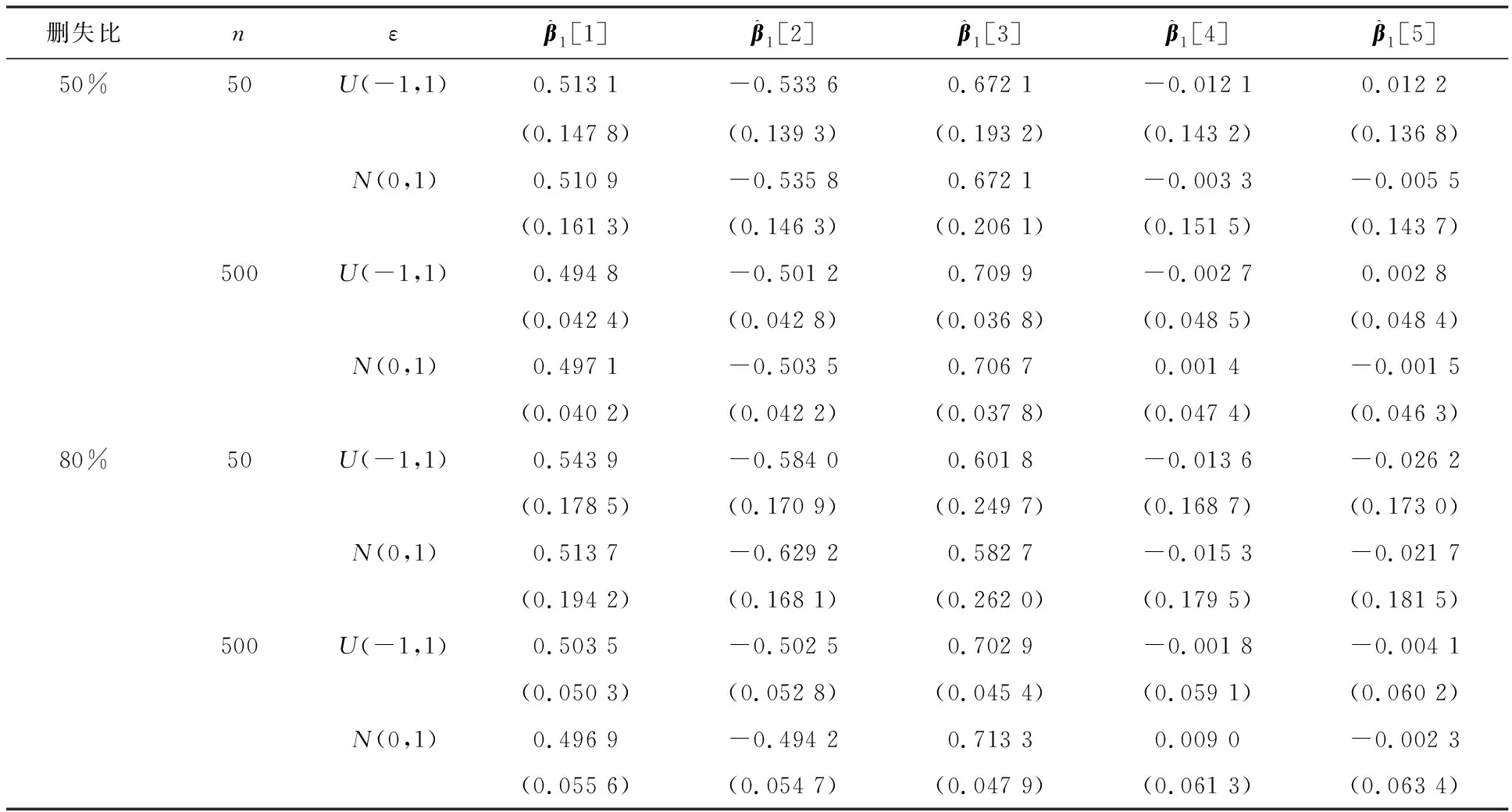
表6 方法2的SIR估计和标准差

续表6

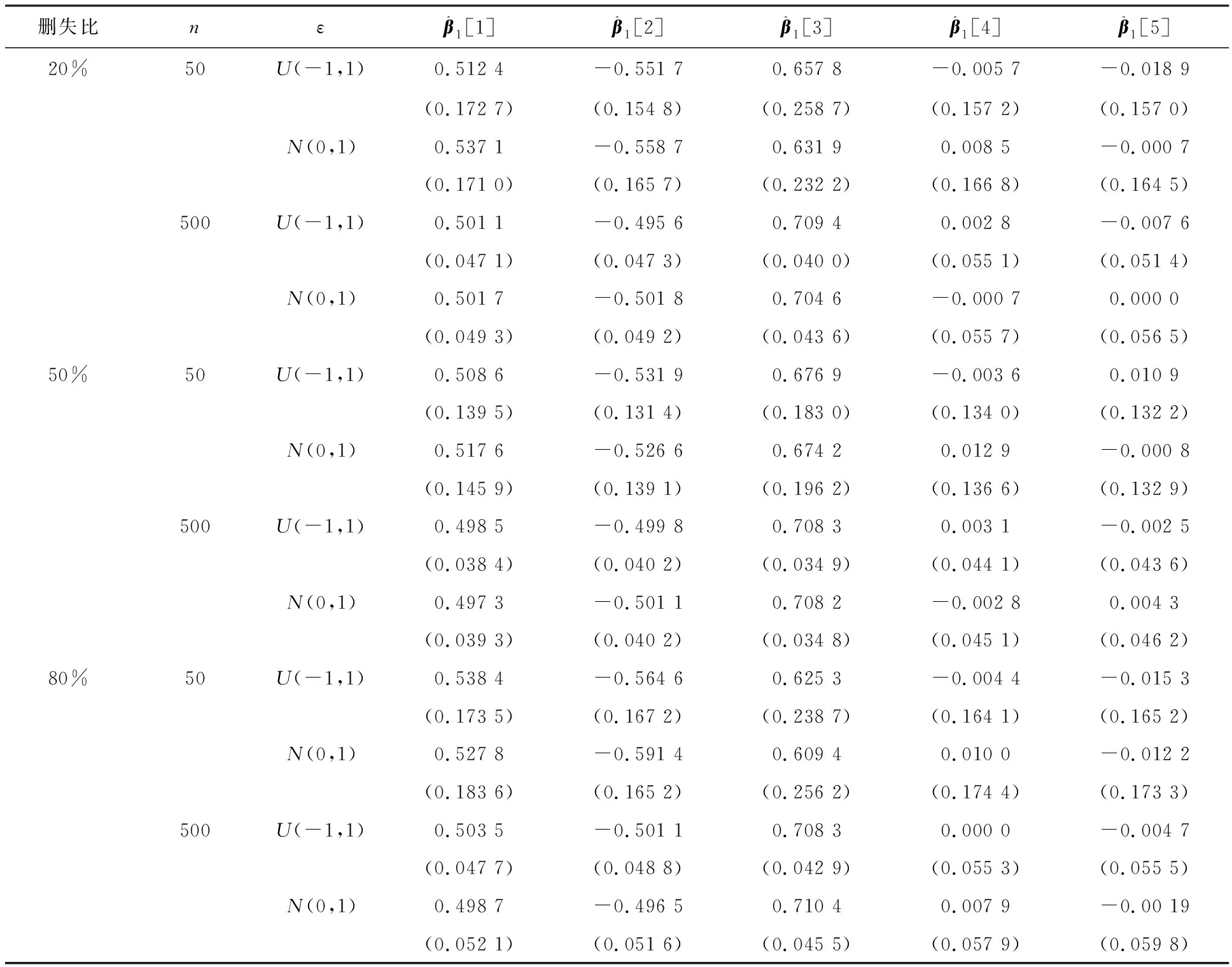
表7 方法3的SIR估计和标准差

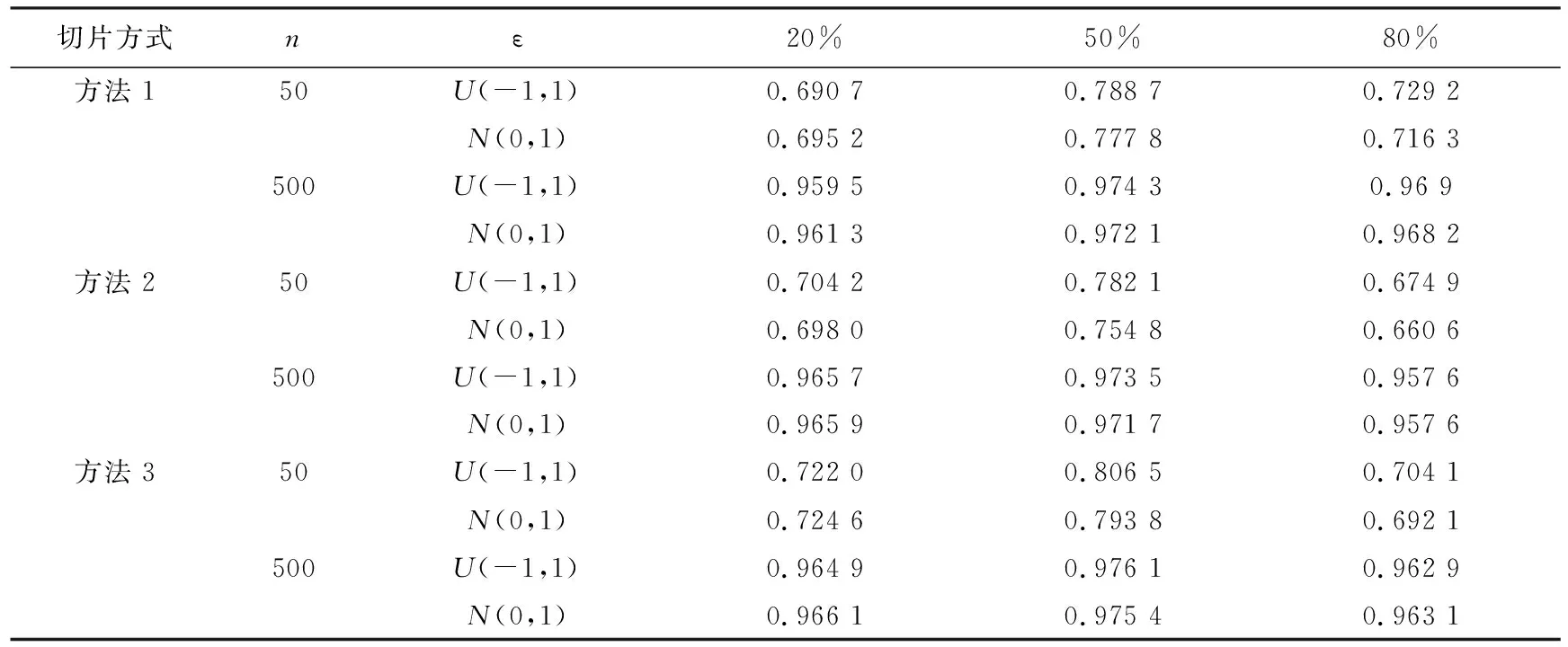
表8 多元相关系数的平方(R2)

表5—7分别展示了在3种切片方式下，SIR估计结果和对应的标准差.从上述结果中可以看出，3种切片方法在不同的删失比下估计值与真实值均较为接近.在不同的误差分布下，估计结果之间的差异不大.随着样本量增大，估计的准确性提高，标准差逐渐减小.

如表8所示，3种切片方法在不同删失比下，R2较大，降维效果较好.在不同的误差设置时，R2数值相差不大.随着样本量的增加，R2也逐渐增大.即样本量越大，估计的中心降维子空间的估计值与真实值更接近.

3 实证应用

本节将SIR方法应用于大鼠胆管增生数据中.数据来源于1977—1980年美国卫生与公众服务部依据国家毒理学计划(NTP)对多溴苯混合物(PBB)进行的毒理学和致癌生物测定实验[14].实验中，对出生7或8周的344只雌雄大鼠分6种剂量注射PBB.其中有314只大鼠的胆管增生患病率数据是可用的.该数据的变量含义如表9所示.

表9 变量说明

使用χ2检验选取1维的中心降维子空间，3种切片对应SIR估计结果如表10所示.

表10 SIR变量选择结果

根据表10可知，3种切片方法下协变量系数相差不大.由系数大小可知，PDD的剂量、大鼠的性别与大鼠的初始体重对胆管增生患病率影响较大，笼子层数的影响较小.在方法2和方法3中，X4的系数接近于0，可以剔除该变量.但在方法1中，该变量系数不能认为接近于0，即不能直接剔除.

4 结语

本文通过赋予等权重方法构造权重矩阵，把切片逆回归方法推广到区间Ⅰ型删失数据中，将重要变量选取出来.研究表明，此方法估计结果与真实值非常接近，标准差较小.在不同切片方法与不同删失比下，其结果相差并不明显.实证分析显示，推广后的切片逆回归方法可以将影响胆管增生患病率的重要变量选取出来.

由于仅讨论区间Ⅰ型删失数据下切片逆回归方法，其他数据类型的切片逆回归方法仍需进一步考虑.本文仅考虑协变量个数小于样本个数的情况，对于超高维数据，可以进一步讨论.