基于极限位移准则和变形预测的滑坡变形潜势分析
2022-05-26李晓斌
李晓斌
1 陕西铁路工程职业技术学院工程管理与物流学院,陕西省渭南市站北街东段1号,714000
黄土坡滑坡是三峡库区具有代表性的滑坡之一,数量多且规模和类型存在一定差异,许多学者对此展开研究,如邓清禄等[1]从变形发育角度出发,构建自重应力条件下的黄土坡滑坡发育模型;简文星等[2]对黄土坡滑坡的成因机制进行分析。上述研究虽然取得一定成果,但多是偏向滑坡结构或成因机制方面,缺乏滑坡变形潜势分析。变形潜势是指滑坡体内部潜在变形能力的强弱,可用于评估潜在滑坡变形的大小。通过变形潜势分析,可为滑坡灾害的变形控制提供一定的理论基础,增加灾害防治的科学性。黄土坡滑坡变形潜势的合理评价可通过两个阶段来实现,分别为滑坡现状变形潜势分析和滑坡变形潜势的发展趋势评价。在滑坡现状变形潜势分析过程中,极限位移准则[3]能有效评价滑坡剩余变形量,因此可利用其进行滑坡现状变形潜势分析;同时,在滑坡变形潜势的发展趋势评价过程中,考虑到变形预测能有效反映滑坡变形的发展趋势,因此可利用其来实现滑坡变形潜势的发展趋势评价。研究表明[4-5],相关向量机(relevance vector machine, RVM)在滑坡变形预测中具有良好的预测效果。为保证预测模型参数的最优性,考虑到模拟退火算法[6]、粒子群算法[7]以及混沌理论[8]在滑坡变形预测中的广泛适用性,利用三者对相关向量机进行优化处理,构建用于滑坡变形预测的优化相关向量机模型。本文以黄土坡滑坡为例,首先利用极限位移准则进行滑坡现状变形潜势分析;然后利用优化相关向量机进行滑坡变形预测,并以预测结果来判断滑坡变形潜势的发展趋势;最后结合两种分析结果,实现黄土坡滑坡的综合变形潜势分析。本文研究可为黄土坡滑坡的变形潜势分析提供一种新思路。
1 基本原理
为准确评价滑坡变形潜势,首先利用极限位移准则分析滑坡现状变形潜势,掌握其既有变形状态;然后以相关向量机为理论基础,构建滑坡变形预测模型,并以预测结果来判断滑坡变形潜势的发展趋势。为保证预测精度,对RVM模型进行核函数优化、模拟退火算法优化、粒子群算法优化和混沌误差弱化处理。基于上述研究思路,具体分析过程如下。
1.1 现状变形潜势模型构建
极限位移准则为:一般情况下可认为滑坡某处的变形破坏具有临界值,即变形达到一定程度时才会出现变形破坏,进而可将该临界值作为滑坡变形的极限位移值Sc,其与现状变形值St的差值大小可作为滑坡变形潜势的现状评价指标,差值越大,表示现状变形潜势越小。但由于滑坡不同位置处的变形条件存在差异,使得极限位移值Sc也随之不同,因此将极限位移值Sc与现状变形值St的差值作为评价指标不合理。鉴于此,本文将相对变形指标Fr作为滑坡现状变形潜势的评价指标,计算公式为:
Fr=St/Sc
(1)
通过变形监测成果可直接统计现状变形值St,因此还需求解极限位移值Sc。研究表明[3],通过双曲线模型可求得极限位移值Sc,即
y=t/(a+bt)
(2)
式中,y为变形拟合值,a、b为拟合参数,t为时间变量。
由式(2)可知,当时间变量趋近于无穷大时,变形拟合值也趋近于极大值,因此利用式(2)可求解极限位移值Sc,即Sc值为1/b。Fr值越大,说明滑坡现状变形的潜势程度越严重,因此可利用Fr值进行现状变形潜势等级划分,具体标准见表1。

表1 滑坡现状变形的潜势等级划分标准
1.2 滑坡变形潜势发展模型构建
滑坡变形预测可用来评价滑坡变形潜势的发展趋势,为保证预测效果,将预测过程分为两步:一是通过RVM模型构建滑坡变形潜势的初步预测模型,同时在预测过程中采用多种算法对参数进行优化处理,以保证预测精度;二是在初步预测基础上,通过混沌理论进行误差修正预测。
相关向量机(RVM)是一种新型预测方法,其首先通过不相干点筛除处理,再保留核心向量,不受Mercer定理约束,因此具有高效的预测能力。在RVM模型的变形预测过程中,若训练样本为{xi,ti,i=1, 2,…,n},则训练过程可表示为:
(3)
式中,wi为权重向量,K(x,xi)为核函数,w0为偏差,zi为噪声。
RVM模型的基本原理参见文献[9-10],限于篇幅,不再赘述。同时,RVM模型虽具较优的预测能力,但其核函数类型及学习因子缺乏客观的确定方法,因此有必要进行寻优处理。
1)核函数优化处理。在RVM模型应用过程中,常用的核函数有Gauss核、RBF核、ERBF核、Sigmoid核,由于构建原理不同,使其在滑坡变形预测中的适用性也存在一定差异,为实现其优化处理,提出对四者均进行试算处理,预测效果最佳者即为RVM模型的核函数。
2)学习因子优化处理。粒子群算法(particle swarm optimization, PSO)已被广泛应用于岩土领域,适用性较强,但其在处理高维复杂问题时易陷入局部极值,而模拟退火算法(simulated annealing, SA)具有概率突跳特性,能在解空间中寻找全局最优解,可有效弥补粒子群算法的缺陷。因此,本文以模拟退火算法优化的粒子群算法(SAPSO算法)进行学习因子优化处理。算法优化步骤如下:
① 初始化设置。规模设置为500,最大迭代次数为600,其余参数随机设置。
② 计算每个粒子的适应度值,并对比所有粒子的适应度值,选取适应度值最优者作为全局适应度值。
③ 确定SA算法的初始温度,并利用交叉验证法计算相应温度条件下的适配值;同时,通过改变温度来更新粒子的位置和速度,以实现粒子的迭代寻优。
④ 计算各粒子的适应度值,并根据模拟退火算法的迭代公式进行退温操作。
⑤ 达到最大迭代次数或期望后停止训练,输出寻优结果,完成学习因子的优化处理。
3)误差弱化处理。前述优化处理虽然可保证RVM模型的参数最优性,但限于滑坡变形的非线性变形特征,前述预测结果仍会存在一定误差,且误差序列具有较强的随机性,混沌特征明显。为进一步提高预测精度,提出利用混沌理论实现误差弱化处理。
首先利用Lyapunov指数法计算误差序列的混沌指数λmax,若λmax>0,说明误差序列具有混沌特性,可利用混沌理论进行误差序列的弱化处理;反之,若λmax<0,说明误差序列不具有混沌特性,无法利用混沌理论进行误差序列的弱化处理。
然后进行误差序列的相空间重构,即
ψi=[εi,εi+τ,…,εi+(m-1)τ]T
(4)
式中,ψi为空间中第i个相点,εi为误差值。以ψi为中心,将其与ψl相点(最近相邻点)间的距离d表示为:
(5)
当d值保持最小时,即可实现误差弱化处理,且误差弱化预测模型可表示为:
‖ψi-ψi+1‖=‖ψl-ψl+1‖eλmax
(6)
最后利用ψl反推出εi+1,即实现误差弱化处理。
将优化RVM模型的预测结果和误差弱化预测结果进行叠加,所得叠加值即为滑坡变形预测值。
通过变形预测结果即可判断滑坡变形潜势的发展趋势,即若滑坡变形增加,说明变形潜势向不利方向发展;反之,变形潜势向有利方向发展。同时,由于不同监测点的变形特征存在一定差异,提出对所有监测点按照不利原则进行变形潜势的综合评价。
2 实例分析
2.1 工程概况
三峡库区黄土坡滑坡区总体呈南高北低的顺向斜坡地形,历史上已经历多次坡体变形影响,致使区内地形具有“陡-缓-陡”特征[11]。据现场调查,区内第四系地层主要分布于斜坡中下部,成因类型主要包括滑坡堆积层、残坡积层和崩滑堆积层;下覆基岩以三叠系巴东组砂、泥岩为主,遇水易软化,并易形成软弱夹层。在三峡库区黄土坡滑坡中,临江1号滑坡是其重要组成部分,据现场调查,滑坡纵向长约770 m,宽约450~500 m,面积约32.5万m2,平均厚度约69.4 m,体积约2 255.5万m3,属超深层巨型滑坡。若临江1号滑坡出现失稳,会严重威胁库区航运安全,因此对其开展变形潜势分析具有必要性。
据现场钻探及调查结果,临江1号滑坡的物质组成具体如下:
1)滑体物质。滑体岩性以碎石土为主,棕红色,中密状态,碎石岩性以泥质灰岩为主,呈次棱角~棱角状,粒间多由粉土充填,土石比例为2∶8~3∶7。
2)滑带物质。滑带岩性主要为粉质粘土,并含有一定的碎石和碎屑,土石比例为6∶4~8∶2,其中粉质粘土多呈可塑状,具稍密~密实状态;碎石和碎屑的母岩成分以泥质灰岩为主。
3)滑床物质。滑坡下覆基岩主要为三叠系巴东组泥质灰岩,中厚层状,层厚为20~40 m,岩体完整性较好,倾向为335°~358°,倾角为34°~47°。
由于临江1号滑坡的潜在威胁较大,为实时掌握其变形状态,对其布设变形监测点,按1次/月频率进行监测,其中,G7监测点位于滑坡体中前部,G9监测点位于滑坡中后部,G11监测点位于滑坡后缘。经多年监测,共得到64期(2006-03~2011-06)变形数据(变形数据为累积总位移数据),结果见图1。可以看出,G7监测点变形最大,变形值达146.87 mm,其次为G9和G11监测点,说明滑坡前部变形要明显大于后部变形。
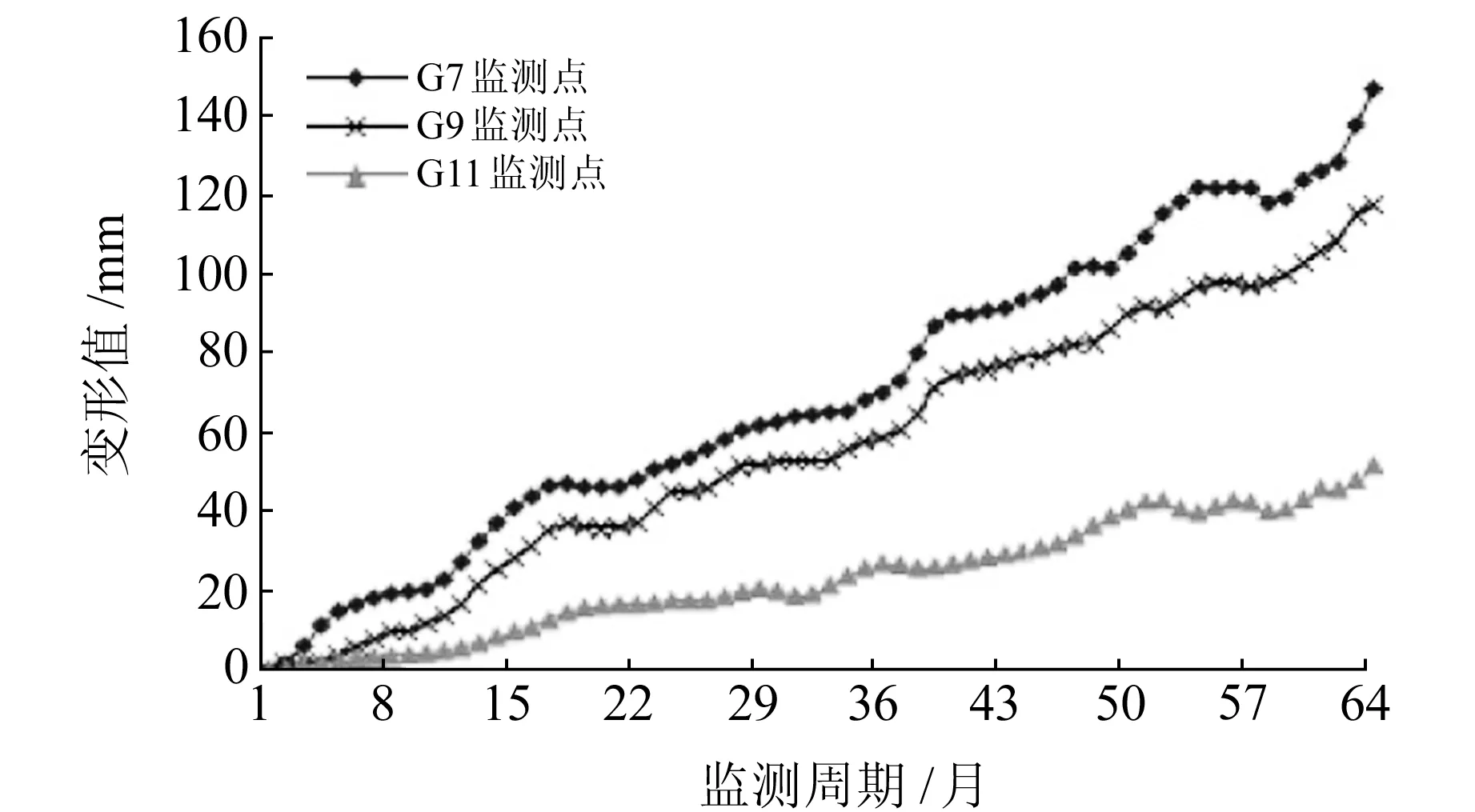
图1 滑坡位移-时间曲线Fig.1 Displacement-time curves of landslide
2.2 现状变形潜势分析
利用极限位移准则进行滑坡现状变形潜势分析,结果见表2。可以看出,3个监测点的拟合度介于0.948~0.973,拟合过程较优;同时,计算得到分级指标Fr值介于0.53~0.77,其中,G7监测点的潜势等级最高,为Ⅳ级,潜势程度属严重;G9监测点的潜势等级为Ⅲ级,潜势程度属中等;G11监测点的潜势等级为Ⅱ级,潜势程度属轻微。

表2 滑坡现状变形潜势分析结果
综合3个监测点的现状潜势分析结果可知,滑坡不同位置处的现状变形潜势存在一定差异:由滑坡后缘至前缘,变形潜势趋于严重。基于不利原则,综合确定临江1号滑坡的现状变形潜势等级为Ⅳ级,潜势程度属严重。
2.3 变形潜势发展趋势评价
利用变形预测进行变形潜势发展趋势评价。为充分验证预测流程的合理性和本文预测模型的滚动预测效果,参照样本分布规律,将预测过程划分为中期预测和后期预测,其中,前者训练集为1~40期数据,验证集为41~46期数据;后者训练集为1~58期数据,验证集为59~64期数据,外推预测4期。
2.3.1 中期预测结果分析
在中期预测结果中,利用G7监测点进行各优化阶段的预测效果对比;再对G9和G11监测点进行中期预测。
1)核函数优化结果分析。按照优化思路,先对4类核函数的预测结果进行统计,结果见表3。可以看出,4类核函数的预测效果存在一定差异,表明进行核函数优化筛选具有必要性;ERBF核函数的的预测精度最好,相对误差均值为2.58%,其次为RBF核、Sigmoid核和Gauss核,因此将ERBF核函数确定为RVM模型的核函数。

表3 不同核函数筛选结果
2)学习因子优化结果分析。在核函数优化基础上,利用SAPSO算法优化RVM模型的学习因子参数,同时为验证SA算法的优化效果,对PSO算法和SAPSO算法的预测结果进行统计,结果见表4。可以看出,在相应验证节点处,SAPSO-RVM模型相较PSO-RVM模型具有更小的相对误差,前者相对误差均值为2.23%,后者相对误差均值为2.47%,说明SAPSO-RVM模型具有更高的预测精度,表明SA算法具有良好的优化效果。
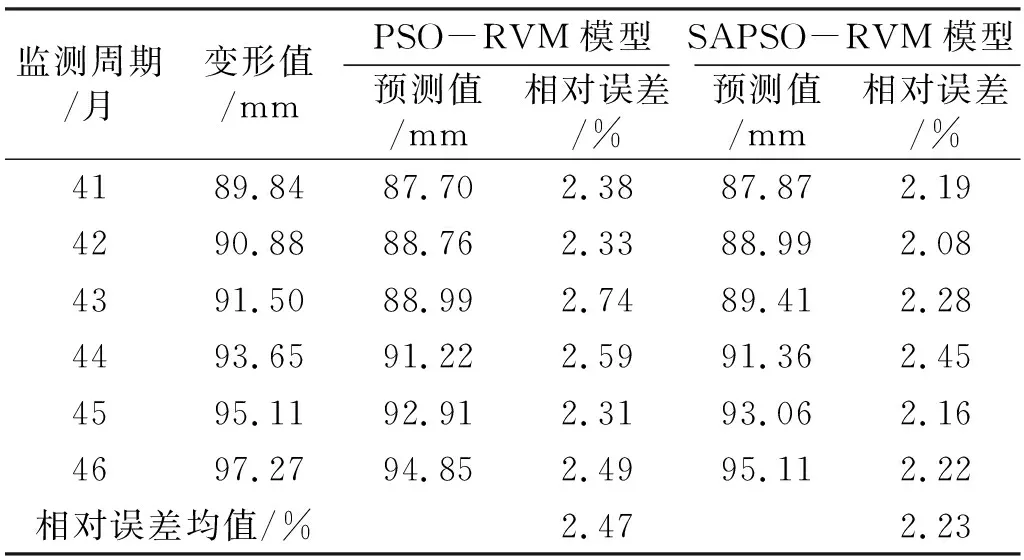
表4 学习因子优化预测结果
为进一步验证SA算法优化处理的必要性,对PSO算法和SAPSO算法在优化过程中的特征参数进行统计,结果见表5。可以看出,SAPSO算法较PSO算法具有更少的迭代次数和更短的训练时间,说明SAPSO算法具有更快的收敛速度;同时,SAPSO算法的局部优化次数为7,PSO算法的局部优化次数为4,表明SAPSO算法具有更强的全局优化能力。

表5 两种算法的特征参数统计
3)误差弱化预测结果分析。利用混沌理论进行误差弱化处理,先利用Lyapunov指数法计算G7监测点误差序列的混沌指数λmax,计算结果为0.052,表明误差序列具有混沌特性,因此可利用混沌理论进行误差序列的弱化处理,误差弱化后的最终预测结果见表6。可以看出,G7监测点预测结果的相对误差介于1.80%~1.98%,变化范围较小,表明预测结果具有较强的稳定性,且相对误差均值为1.92%,具有较高的预测精度。
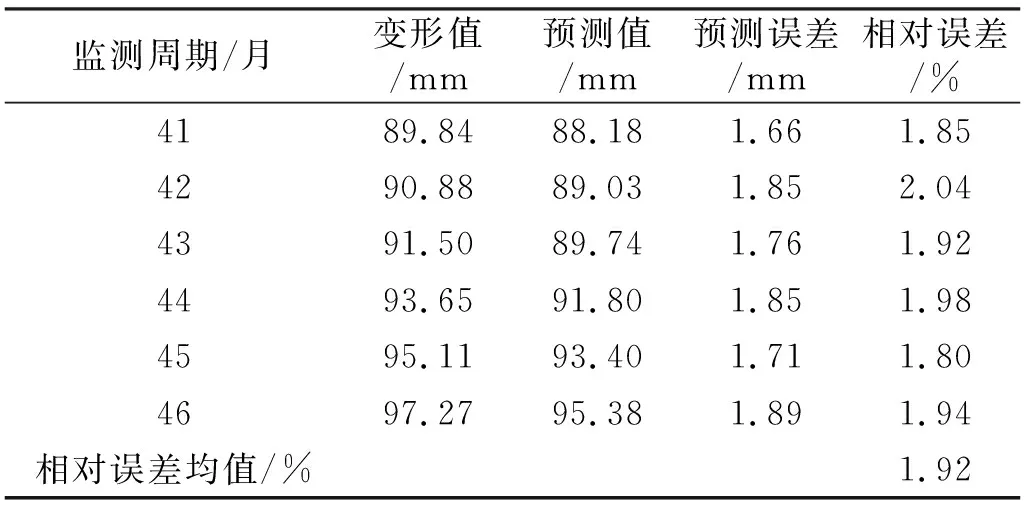
表6 G7监测点最终预测结果
对比前述G7监测点的逐步优化过程可知,递进优化处理能有效提高预测精度,所得最终预测结果的预测效果较优,初步验证本文预测思路的有效性。
4)G9和G11监测点中期预测结果分析。类比G7监测点的预测过程,对G9和G11监测点进行中期预测,表7为预测结果。可以看出,在G9监测点的预测结果中,最大、最小相对误差分别为2.03%和1.76%,相对误差均值为1.89%;在G11监测点的预测结果中,相对误差介于1.73%~2.04%,均值为1.85%,G9和G11监测点的预测结果相当,均具有较优的预测精度。
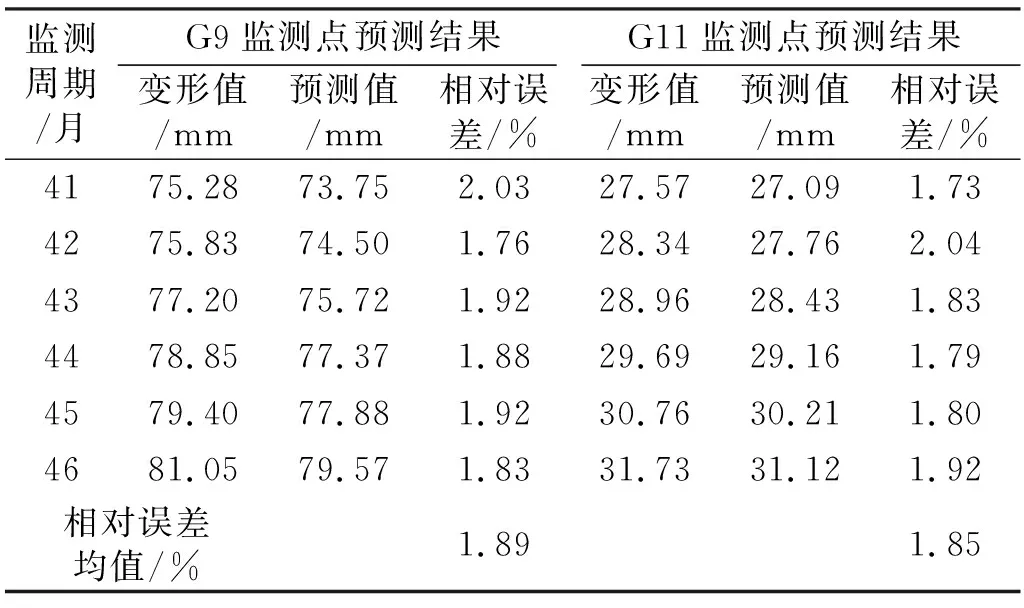
表7 G9和G11监测点中期预测结果
2.3.2 后期预测结果分析
在滑坡中期预测基础上进行滑坡后期变形预测,以进一步验证本文预测模型的合理性,同时实现滑坡变形潜势发展趋势评价。表8为滑坡后期预测结果统计,可以看出,3个监测点的相对误差均值介于1.81%~1.93%,波动范围较小,进一步验证本文预测思路不仅具有较强的稳定性,还具有较高的预测精度。同时,通过外推预测结果可知,滑坡在3个监测点的变形会持续增加,变形潜势向不利方向发展。
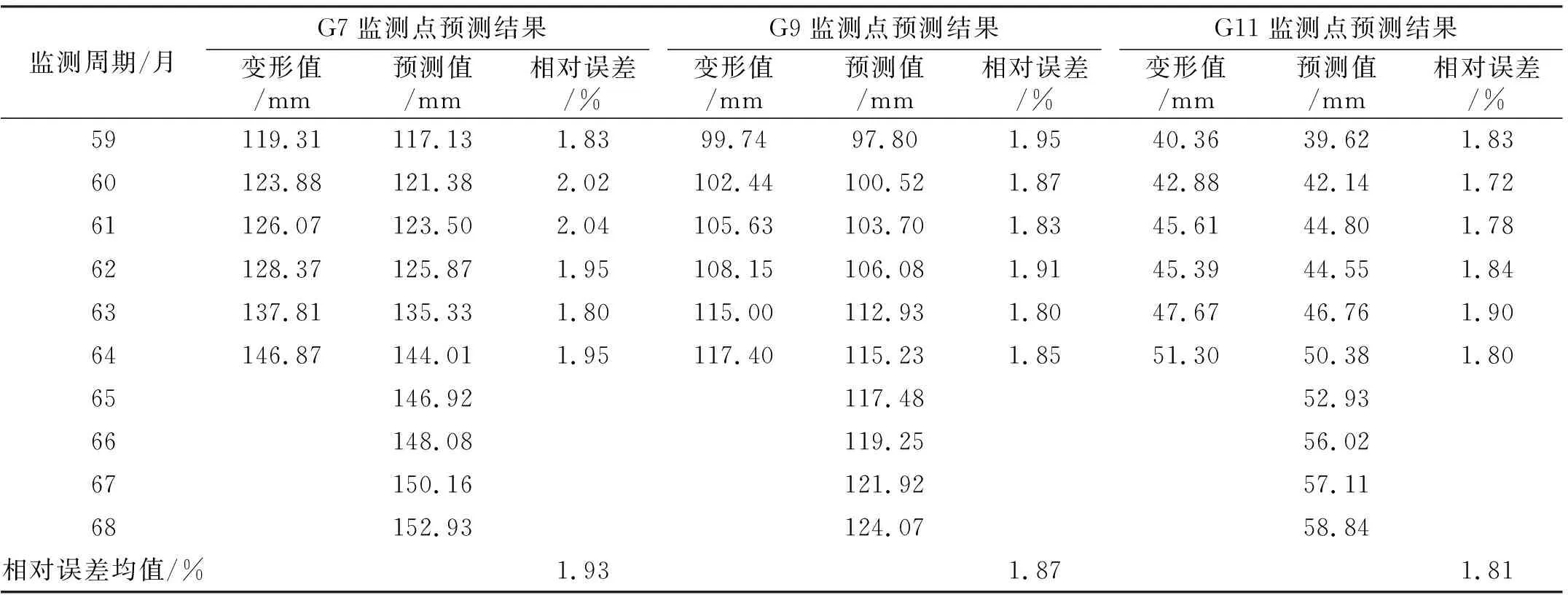
表8 滑坡后期预测结果
通过上述分析可知,本文预测模型在滑坡中期、后期的预测结果均较好,不仅具有较高的预测精度,还具有较强的稳定性;同时,外推预测结果表明,滑坡后续变形仍会进一步增加,变形潜势向不利方向发展。
2.4 滑坡变形潜势综合分析
通过前述滑坡现状变形潜势分析和变形潜势发展趋势评价可知:
1)现状变形潜势分析结果显示,G7监测的潜势等级最高,为Ⅳ级;G9监测点的潜势等级为Ⅲ级;G11监测点的潜势等级为Ⅱ级。基于不利原则,综合确定临江1号滑坡的现状变形潜势等级为Ⅳ级,潜势程度属严重。
2)变形潜势发展趋势评价结果显示,本文预测模型具有较高的预测精度,适用于滑坡变形预测,且由外推预测结果可知,滑坡在3个监测点的变形会持续增加,变形潜势向不利方向发展。
综合上述分析结果可知,临江1号滑坡的变形潜势处于不利状态,后期失稳可能性较大,建议加强灾害防治,避免成灾损失。
3 结 语
通过对临江1号滑坡的变形潜势进行分析,得到以下结论:
1)不同监测点的现状变形潜势状态存在一定差异,大致变化规律为:由滑坡后缘至前缘,变形潜势趋于严重。同时,基于不利原则可知,临江1号滑坡的现状变形潜势等级为Ⅳ级,潜势程度属严重状态。
2)变形预测分析结果表明,滑坡在3个监测点的变形会持续增加,变形潜势向不利方向发展。结合现状变形潜势分析结果可知,临江1号滑坡的变形潜势处于不利状态,后期失稳可能性较大,应加强灾害防治,以保证航运安全。
3)在预测模型构建过程中,传统单一模型已难以满足精度要求,通过递进优化处理能有效提高预测精度,并增加预测结果的稳定性。
