严寒地区飞机温度环境分析与预测方法研究
2022-05-26李贺张建军傅耘石慧万军
李贺,张建军,傅耘,石慧,万军
(1.中国航空综合技术研究所,北京 100028;2.西南技术工程研究所,重庆 400039)
引言
严寒地区是指全年有3个月以上时间冰雪覆盖,月极端气温在-30 ℃以下的区域[1]。我国严寒地区分布广泛,极低的气温和长久的低温持续时间严重影响了航空装备的使用性能,由低温环境引发的飞机故障覆盖发动机、机载电子产品、机械产品及机电产品,涉及起落架、燃油、电线电缆、飞控、液压等各个系统,极大影响了飞机的作战效能。尤其是对于服役于东北、西藏等严寒地区飞机,在服役期间有超过90 %的时间处于地面停放状态[2],长久低温环境使得低温疲劳不断累积,不仅降低了飞机的可靠性,对其寿命也产生了不利影响。另外,当前的实验室低温环境试验条件缺乏针对性,无法准确反映设备所处的极限诱发环境温度。因此,确定飞机真实服役环境条件下各舱室温度变化规律,准确掌握飞机在严寒环境下的全机温度分布,对于解决飞机低温故障频发问题,优化机载设备低温环境试验条件,提高飞机维修保障能力有着重要意义。
限于极限环境出现的窗口期,一般无法获得装备在真实服役条件下的极限温度数据,工程上通常采用温度预测方法,对温度环境条件进行预测,以指导环境适应性设计与试验条件的制定。目前,平台温度数据预测方法主要分为数据驱动法和流体力学计算(CFD)仿真法,其中,数据驱动法又包括统计归纳法[3]、基于物理传热机制的建模方法以及神经网络法[4-7],相较于统计归纳与神经网络等依靠数据本身变化规律的方法,基于物理传热机制的方法同时兼顾的装备的物理状态变化以及实测数据,具有更高的准确度以及泛化能力。S.P.Mahulikar等[8]应用物理传热机制模型对飞机后机身蒙皮温度进行了预测。王浚[9]根据飞机座舱的传热机制推导了座舱温度的数学模型。傅耘等[10]基于实测数据建立了飞机平台动态温度预测模型,通过输入飞机飞行的高度和马赫数,获取飞机后设备舱的温度。罗成等[11]基于热网络模型预测了导弹舱室在贮存环境下的温度变化。PANG等[12]基于热网络模型建立了某型无人机在高海拔长航时过程中的温度预测模型,并通过试验进行验证。国内外对于停放状态下的飞机整机平台环境研究较少,而在真实的严寒服役条件下的研究则基本处于空白。
本文基于某型飞机在我国西南某区域严寒区域下的真实服役停放状态数据,对飞机结构进行二次分区,研究了飞机温度诱发环境的分析方法,确定了整机不同舱室的温度变化规律,并以外界气候环境温度为输入,采用数据统计分析与物理传热机制方法,分别建立飞机温度的双层回归模型和多模式换热模型,实现对飞机各舱室温度的预测,为机载设备的环境适应性设计、试验与精准保障提供支撑。
1 严寒地区全机温度环境实测与分析
本文针对某型飞机开展了全机温度环境实测工作,并对其温度环境进行分析与研究。飞机所处区域为我国西南某地区,属于典型的严寒地区。飞机露天停放于外场停机坪,无遮挡物。为了充分了解全机环境分布,在飞机座舱、设备舱、发动机舱、起落架舱、蓄电池舱、中央设备舱、尾梁、蒙皮等8个区域设置24个温度测点,1个外界百叶箱温度采集点。测量时间选择为温度环境最为严酷的1月份夜间,测量周期1周。
1.1 温度实测概况
严寒环境测量采用IMC SPARTAN数据采集记录系统,T型热电偶进行温度采集,热电偶测量精度小于0.5 ℃,温度响应时间为0.5 s,测量频率1 Hz。详细测点分布如表1所示。
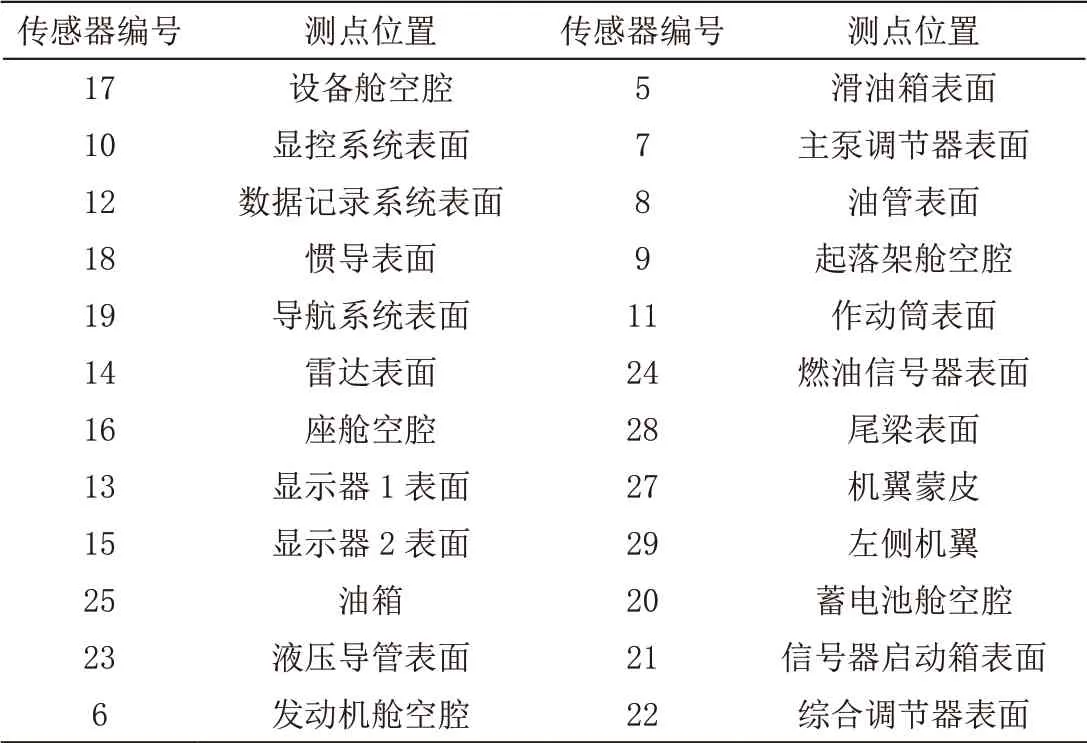
表1 温度测点分布
1.2 全机温度环境分析
环境分区是进行全机温度环境分析的基础。本文环境分区是通过两步完成的:一是根据飞机平台的传热特性,将相似传热结构的舱室进行归类[13];二是在数据分布统计的基础上,对结构分区结果进行调整。最终,全机分为设备舱、座舱、燃油和液压系统、发动机舱、起落架舱、机翼和尾梁六部分,具体如图1所示。
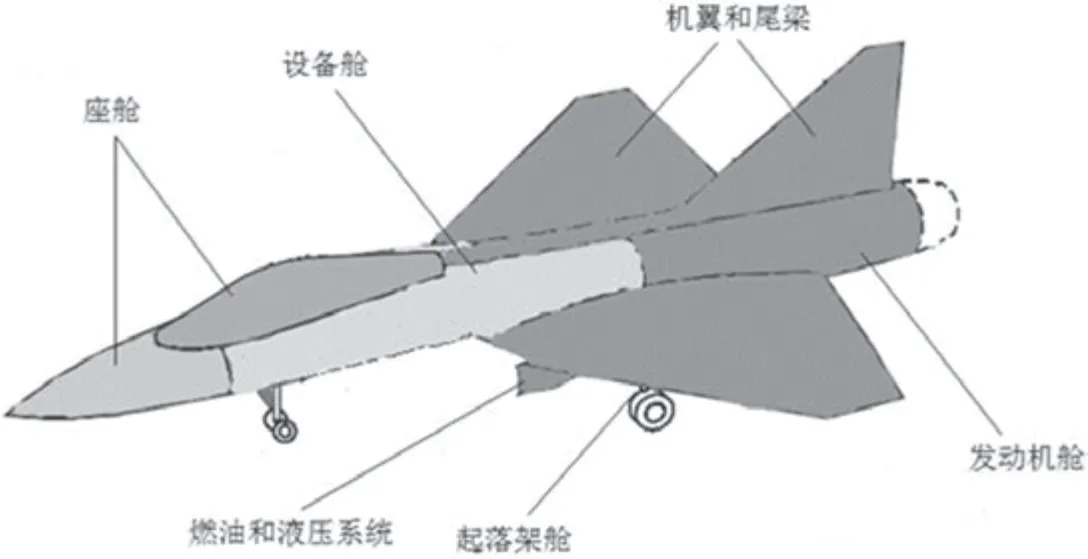
图1 某型飞机温度环境分区示意图
以2020年1月16日为例,按照分区结果给出整个夜间各个区域的温度数据,其中,舱室温度取该舱内各测点温度平均值。为显示各舱室温度与外界温度环境关系,将百叶箱温度也绘入图中,具体温度分布如图2所示。
通过图2温度变化曲线可以看出,飞机在夜间外场停放期间,各区域温度与外界环境正相关,随时间推移呈平稳下降的趋势,最终趋于一定值。其中,发动机舱温度最高,机翼和尾梁温度最低,座舱、设备舱、燃油和液压系统、起落架舱内温度依次降低,平稳时,各区域温差减小,全机温度分布趋于均匀。

图2 1月16日各区域温度变化曲线
发动舱温度明显高于其他舱室,这是因为当日清晨存在试车,燃烧释热使得发动机附近初始温度较高导致的。机翼和尾梁温度最低,甚至低于外界大气温度,主要有以下三方面原因:一是相对于机内设备,蒙皮直接与外界环境接触,无防护措施;二是由于蒙皮为金属材料,热容较小,热量变化较快;三是夜间蒙皮对外空间辐射散热。
整体而言,各舱室设备诱发环境温度相差较大,最大温差>10 ℃,针对不同的舱室内的设备,在进行低温环境适应性设计与制定低温环境试验条件时,应采取不同的方法及量值。
2 双层回归分析温度预测模型
2.1 温度预测模型的建立
双层回归分析是指通过两次回归分析,确定变量之间的函数关系。本部分建立温度预测模型的思路是:以百叶箱温度(即外界气温)T0为自变量,考虑环境因素的影响,建立舱室温度Ti变化的函数关系。
飞机在外场停放时,外界气候环境是其内部温度变化的主驱动力。低温、日照、大风、降雪等也会对飞机内温度环境产生影响。由前文分析可知,外界大气温度为飞机温度变化的冷源,低温将直接导致舱室内温度降低;日照提供了热辐射的热源,可提高飞机温度;大风加快了空气流动,使得强迫对流换热量增加;雪花可以阻碍机体结构的散热,但是融化时又会吸热导致飞机温度降低。除此之外,不同舱室由于所处的位置不同,与外界热交换的情况也有所不同。因此,气候环境因素和结构因素是影响飞机温度环境变化的关键。
为避免气候因素干扰,选取晴朗无风夜间实测数据进行分析,此时建立的模型只与飞机结构相关。数据再现外界气温与机内各测点温度变化情况,可发现各测点温度与外界气温近似呈明显的线性关系。由于发动机存在试车状态,温度远高于正常停放状态,故暂不分析。采用线性回归算法,对上述各测点关系拟合,得到各测点随气温变化关系系数如表2所示。其中,k为斜率,b为截距,r2为拟合优度。

表2 晴朗无风夜晚系数拟合表
根据系数拟合情况,对飞机进行二次分区。各区域回归方程如下:
舱室Ⅰ,T1=0.996T0+0.8425;
舱室Ⅱ,T2=1.670T0+13.8437;
舱室Ⅲ,T3=1.464T0+10.1316;
舱室Ⅳ,T4=2.051T0+23.4483;
舱室Ⅴ,T5=1.115T0+3.7393;
舱室Ⅵ,T6=1.080T0+1.2020。
由此得到晴朗无风夜间飞机各舱室与外界气温之间的定量关系。
考虑到大风、降雪等其他影响因素,需要对上述模型进行修正。选取典型的风雪天气实测数据,对其进行线性回归拟合,得到系数与k、b之间关系分布如图3所示。
由图3可知,添加了风雪影响的系数k2,b2与晴朗无风条件下的系数k,b之间存在很好的线性关系。对其进行回归拟合可得:k2=2.216k-0.9528,b2=1.524b+5.5539。将 其带入晴朗无风环境模型,即可得出飞机舱内温度与外界气温的定量关系。

图3 考虑风雪因素的模型系数与晴朗无风模型系数关系
2.2 模型检验与误差分析
为检验上述模型的准确性,首先任选一未参与参数拟合的无风天气温度数据进行模型精度检验,本文选取1月14日舱室Ⅰ、Ⅵ的温度测量结果,预测结果及误差如图4和图5所示。
由图4和图5可知,基于晴朗无风天气实测数据建立的温度预测模型具有较好的精度,针对不同舱室,预测的最大误差稳定在2 ℃以内。

图4 晴朗无风夜晚舱室Ⅰ温度预测值及误差
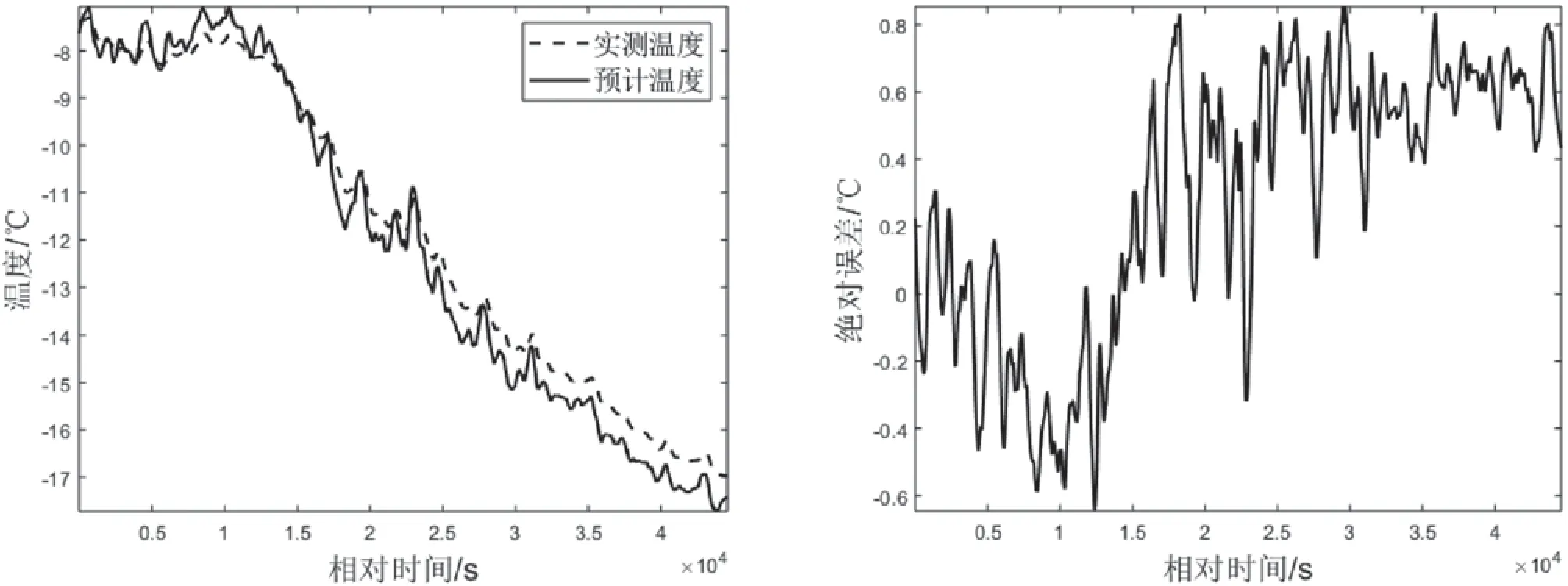
图5 晴朗无风夜晚舱室Ⅵ温度预测值及误差
任选一未参与参数拟合的风雪天气温度数据进行模型精度检验,本文选取1月16日舱室Ⅰ、Ⅵ的温度测量结果,预测结果及误差如图6和图7所示。
分析图6和图7可知,在晴朗无风模型的基础上,考虑风雪因素后,模型的预测精度有所下降,遍历所有区域的预测结果,模型最大误差为3.84 ℃。因此在实际应用过程中,应准确识别飞机所处的气候环境,从而选择相应的温度预测方法。
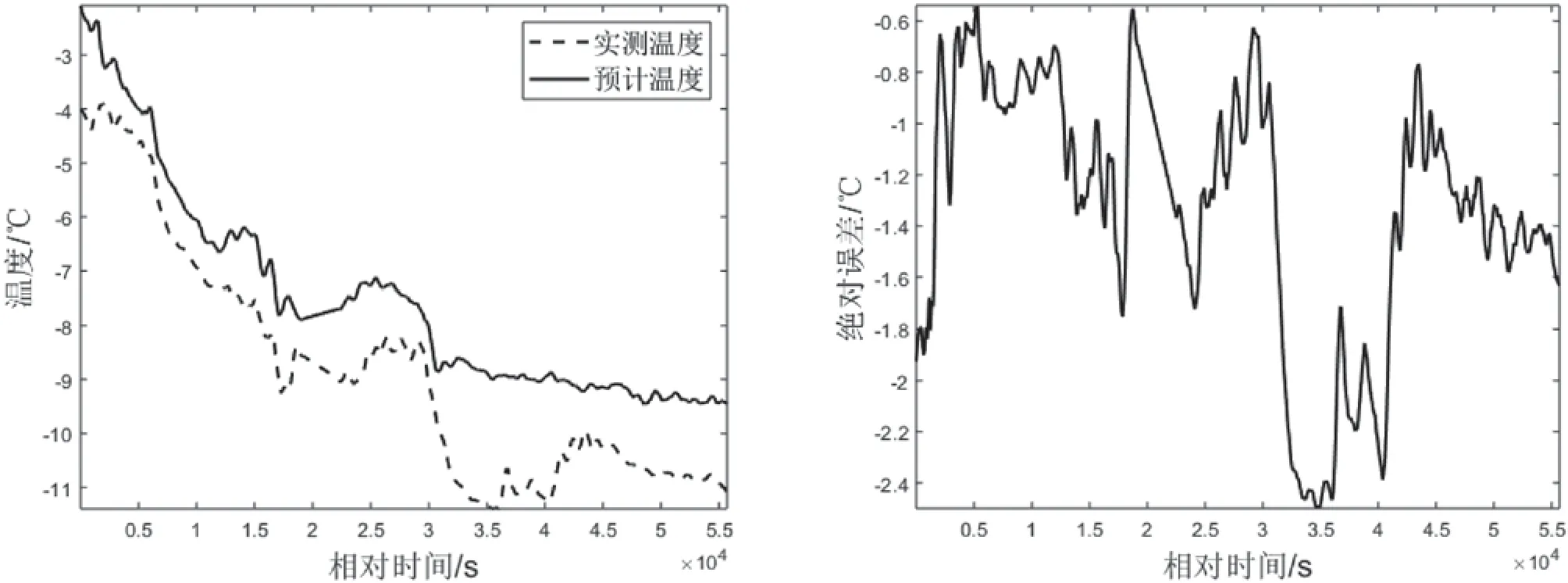
图6 添加风雪因素后的舱室Ⅰ温度预测值及误差
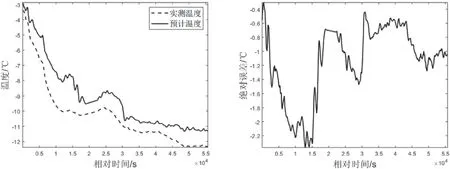
图7 添加风雪因素后的舱室Ⅵ温度预测值及误差
3 多模式换热温度环境预测模型
3.1 温度预测模型的建立
上文利用双层回归算法可以较为准确的预测飞机停放时各舱室的温度,由于数据驱动的特性,未能体现飞机热环境的形成与传递机制,因此模型的应用受到较多限制。为建立更加准确、应用更广的预测模型,本部分对飞机的传热机理进行分析,采用集中参数法,建立温度预测模型。建模的思路是:以某一舱室为研究对象,通过分析其内外传热关系,建立基于传热机制的物理模型,基于实测数据对模型系数进行拟合,最终得到该舱室内温度随外界气温的变化关系。
飞机停放于外界停机坪,其热环境主要由内外环境共同作用决定。内环境是指飞机内部空气、设备、壁面(包括桁架)之间的换热,主要包括舱内设备工作发热、环控系统冷却、设备与设备之间的热辐射、设备与内壁(包括桁架)间的热传导及热辐射、设备与环控冷却气间的对流换热、壁面与空气间的对流换热、蒙皮与内壁之间的导热等。外环境是指以飞机为整体,与外界发生的质量与能量交换,主要包括太阳对飞机表面的辐射、上层空间对飞机上表面的辐射、地表对飞机下表面的辐射、飞行过程中外部气流与蒙皮间产生的气动热等。
以飞机蒙皮为例,由于是夜间停放,且舱内设备和环控系统均不工作,忽略地面辐射,则其热耗散方式主要包括与外部空气对流换热、与外部空气间的热辐射以及与机体内壁面间的热传导。根据能量守恒定律,可获得蒙皮的热流方程如下:
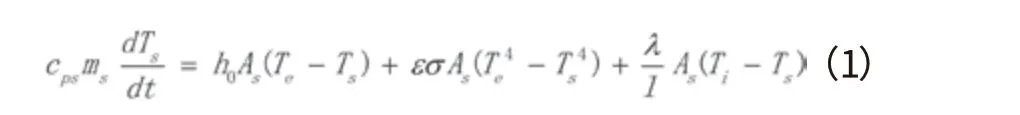
式中:
cps—蒙皮材料的热容;
ms—蒙皮质量;
h0—蒙皮与空气的对流换热系数;
ε—蒙皮发射率(黑度);
σ—斯忒藩-玻尔兹曼常量,其值为5.67×10-8W/(m2·K4);
λ—导热系数;
l—壁面厚度;
AS—蒙皮面积;
t—时间;
TS—蒙皮表面温度;
Ti—壁面内表面温度;
Te—外界气温。
考虑到蒙皮温度主要随外界气温变化,受内部导热影响较小,故忽略壁面导热的影响。又上述各参数中,热容、质量、面积等系数均为常数,故上式可简化为
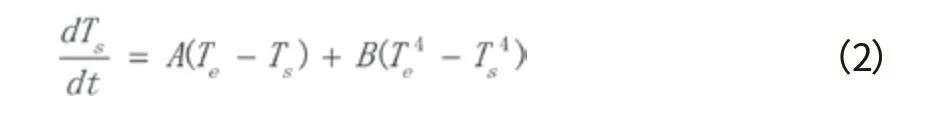
式中:
A、B—常数。

将式(2)进行离散化,得到方程如下:
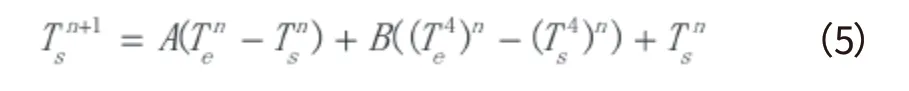
式中:
上标n—第n时刻的取值。
任取三天温度实测数据(含风雪、晴朗天气),对方程(5)进行参数拟合。拟合方法选择逐步回归法,在不断引入自变量的同时,剔除不显著变量,直至方程不再引入和剔除变量即达到“最优”为止。得到参数拟合结果如表3。

表3 参数拟合表
最终获得模型方程如下:
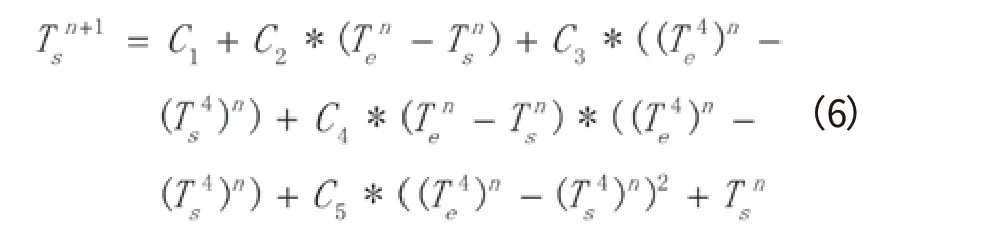
对于飞机内其他舱室的温度,可采取相同办法进行热环境分析,并引入预测的蒙皮温度,最终获得其温度的预测值,由于方法相同,本文不在此赘述。
3.2 模型检验与误差分析
为检验上述模型的准确性,任选一未参与参数拟合实测温度数据进行验证,本文选取1月15日机身蒙皮的测量结果,预测结果及误差如图8所示。
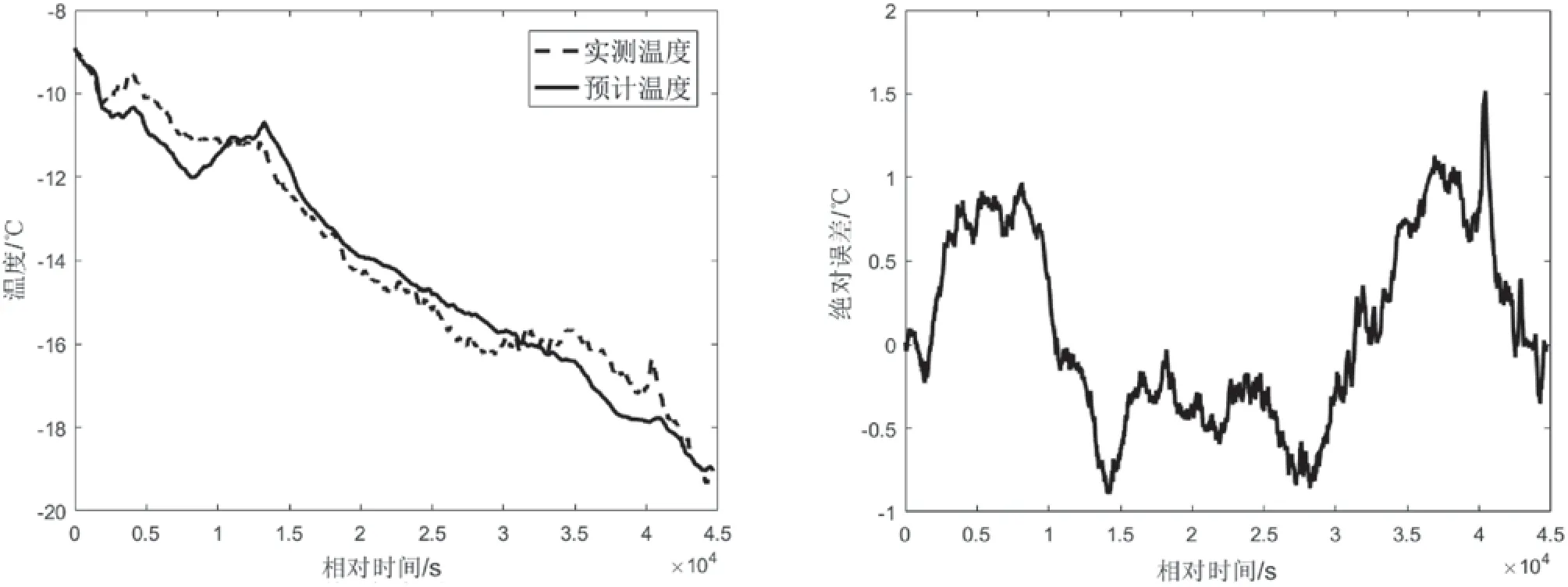
图8 多模式换热模型蒙皮温度预测值及误差
对实测温度与模型预测温度进行统计分析,结果见表4。其中,最大偏差:

表4 数据统计分析结果

平均偏差
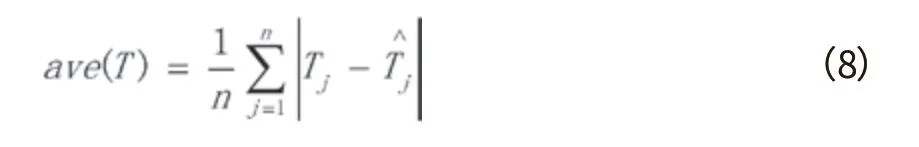
相关系数为
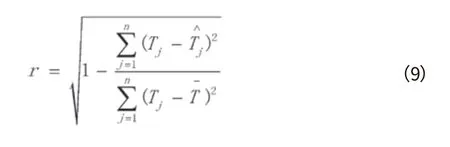
式中:
Tj—第j个温度值;
n—测量的数据点个数,本样本n=44666。
由图8及表4可知,本文提供的温度预测模型具有较好的精度,对于机身蒙皮温度的预测,最大误差不超过2 ℃。以蒙皮温度为输入,建立其他舱室与蒙皮之间的热平衡方程,求解得到各舱室温度分布。统计计算结果,其他舱室预测最大误差不超过3 ℃。相较于双层回归模型,该模型虽然建模过程较为复杂,但是准确度更高,适用范围更广。
4 结论
本文通过对停放于某严寒地区飞机的实测数据进行获取、分析与预测,明确了严寒环境下全机温度环境的变化规律,建立了准确的全机温度诱发环境的预测模型。形成主要结论如下:
1)在进行温度环境分析与预测时,良好的环境分区是工作开展的基础,本文根据飞机不同结构的传热特性与数据分布情况,将全机分为6个区域,分析了不同区域下全机温度变化情况,获得了全机温度变化规律:严寒环境下,飞机在停放过程中,其内部各舱室温度与外界温度变化正相关,同时受到机身结构位置与大风、降雪等气候环境的影响,机翼和尾梁等外露部分是全机温度最低区域。
2)分别基于回归分析与传热分析方法建立了温度预测模型。其中,双层回归模型建模方法相对简单,对于晴朗无风夜晚预测精度较高,在风雪天气精度有所降低,最大误差不超过4 ℃;多模式换热模型建模方法相对复杂,可准确表征飞机的热环境形成与传递机制,预测结果更为准确,最大误差不超过3 ℃。在进行工程应用时,应根据预期精度要求与数据信息情况进行选择,如对精度要求不高,外界气候信息掌握较为全面时,可采用回归分析方法。
3)通过温度环境预测模型,掌握全机温度环境严酷程度,可应用于不同区域舱内设备的环境适应性设计要求准确提出、环境试验条件准确确定和精准保障等方面,对于装备环境适应性与环境试验工作的提升具有一定价值。
