基于MATLAB的前方交会测量在圆曲线主点测设中的应用研究
2022-05-25张培
张 培
(甘肃省庆阳林业学校,甘肃 庆阳 745000)
0 引言
圆曲线主点测设的常规方法是:主点里程计算与测设同时进行,线路的交点里程由丈量得出,主点里程根据交点里程推算,而主点的测设,由交点桩沿后视方向,量取切线长度,得出曲线起点的位置,由交点桩沿前视方向,量取切线的长度,得出曲线终点的位置,由交点桩沿分角线方向量外距,得到曲线中点的位置,分别把标好桩号的木桩打入相应的位置上。由此可见,主点测设的方法中,距离的丈量和测设的关键就是交点位置的确定,但这种方法并不能检核交点的坐标精度,并且数据运算量少。仅能适用于曲线长度小于40 m、地形起伏不大、不需要进行详细测设的圆曲线。
而基于MATLAB的前方交会测量方法,直接测出多个主点的坐标值,特别是对于交点的坐标,可以利用交点落在图形对称轴上的特点,由对称轴两侧的主点推算位于对称轴上的交点坐标值,同一个交点的2组坐标值可以相互检核,只要其精度在点位移e点要求的范围内,就可作为符合工程要求的主点。
1 原理要点与工程意义概述
在道路测量中,曲线道路主点测设的几何模型与交会测量的数学模型类似,因此将求圆曲线道路主点的坐标问题,转化为求交会测量中点(交点)的坐标问题,为此可用前方交会测量方法得出圆曲线主点(交点)坐标,其坐标的精度可用前方交会测量的点位移e点判断,该值不大于测图比例尺的2倍为宜。
道路曲线主点坐标精度的提高,对实际工程而言意义重大。一方面主点测设坐标的精度提高对长距离曲线,进行详细测设的精度提高有很大的帮助;另一方面,在公路或者铁路上,高速行驶的汽车或者火车等,从平面直线路段驶入曲线路段或者由曲线路段驶向直线路段的过程中,在曲线与直线的交汇处,离心力的变化比较大,对交通工具舒适和安全都会产生影响。为了使离心力渐变符合交通工具的轨迹,设置一段曲率半径渐变的曲线在直线和圆曲线之间,有非常重要的工程意义。
1.1 圆曲线道路的基本模型
圆曲线的道路模型图如图1所示,线路改变方向的点在转折点JD处(此点称为交点),即α为转折角,半径为R的圆曲线为构架的圆的半径,圆曲线的第一个关键点是起点,此点称为直圆点ZY,圆曲线的第二个关键点是中点QZ,圆曲线的第三个关键点是终点,此点称为圆直点YZ,这3个点称为圆曲线的主放样点,它们的精确性直接关系到曲线的平滑性。
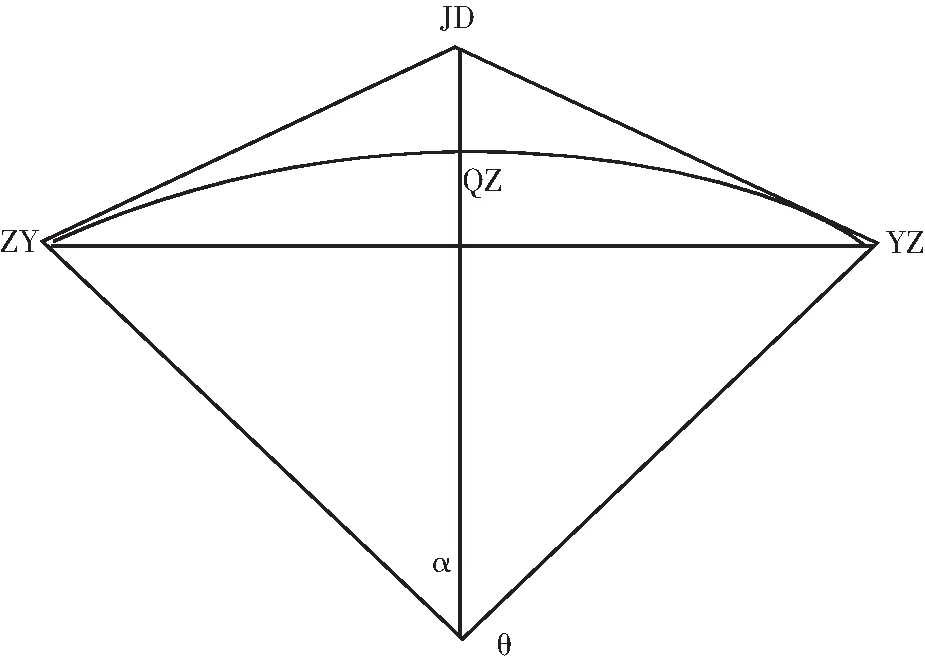
图1 圆曲线主点元素
通过研究圆曲线道路图形的模型特点发现其与交会测量的模型图类似,因此关于求解圆曲线道路中线点坐标的问题,可以转化为前方交会和后方交会的坐标求解问题。
1.2 前方交会测量原理
控制点A、B的坐标已知,在其上分别安置仪器,由此观测得到水平角α和β,然后由相关的公式计算待定点P的坐标,称这种方法为前方交会。
在三角形中,未测定的第三个内角γ,可以由三角形的内角和公式计算得到,即
γ=180°-(α+β)
许多同学认为,和都是H3PO4电离后产生的离子,而且都带负电荷,应该是可以大量共存的。事实上,由于电离出H+的程度大于其水解的程度,使溶液呈现酸性,而在溶液中只能水解结合H+,使溶液呈现碱性,一个呈酸性的离子和一个呈碱性的离子是不能大量共存的,两种离子相遇后,它们之间会发生H+的传递,而最终形成,反应的离子方程式如下:
(1)
然后应用余切公式:
(2)
为了保证交会点的精度,交会角γ应在30°~150°。为了检核精度,进行角度观测时,通常由A、B、C 3个坐标已知的点分别向P点进行,如图2所示,即在3个已知点上观测了2组α1、β1和α2、β2。

图2 三点前方交会

(3)
点位移为:
(4)
规范规定,当位移不大于精度的2倍,即
式中,M为实际测图的比例尺的分母。
取平均值作为p的最后坐标:
(5)
1.3 待求点p坐标的精度指标可作为圆曲线主点测设指标的原因
待求点p是左右两部分的交汇点,当施工作业从两段开始进行时,中间点能够交会在一起成为判断曲线道路平滑性指标的关键因素。
从上述理论分析可知,将圆曲线分为左右两个部分,然后把这两部分转为2个三角形,最后划归为求同一个交点坐标的问题,只要坐标的误差的指标在允许的范围之内,就可以达到精度的要求。
1.4 前方交会测量MATLAB程序实现的主要代码
前方交会测量法是在单三角形法的基础上,由2个相邻的三角形的邻边推算待求点的坐标,该代码的实现方法是以2个对称的三角形为例,对公式(2)余切公式运用了代码实现。
Function[x,y]=QFJH(x1,y1,α,x2,y2,β)
%%前方交会
α=dms_rad(α);
(内角α)
β=dms_rad(β);
(内角β)
x=x1.*cot(β)+x2.*cot(α)+(y2-y1);
(余切公式计算x坐标的分子)
x=x./(cot(β)+cot(α));
(余切公式计算x坐标的分母)
y=y1.*cot(β)+y2.*cot(α);
(余切公式计算y坐标的分子)
y=y./(cot(β)+cot(α));
(余切公式计算y坐标的分母)
2 工程案例验证与分析
前方交会的案例验证与分析如表1所示,前方交会测量数据处理的方法是,求解2个对称三角形位于对称轴上的交点的坐标,两次运用了余切公式,得出同一个点的2组坐标值。这2组坐标值的平方之和的根式的值,在e点要求的范围之内,即该值不大于测图比例尺的2倍。故可以得出该方法得到的坐标精度满足要求,验证了该方法运用于圆曲线道路的主点坐标求解的可行性。

表1 前方交会的案例验证与分析
3 结论
1)基于MATLAB的前方交会测量在圆曲线主点测设中的应用,使距离丈量和主点测设中起关键作用的交点坐标,其精度的判断有了明确的指标。需要明确的是曲线长度小于40 m、地形起伏不大、不需要进行圆曲线的详细测设,这时主点坐标的精度非常重要。
2)初步尝试使用MATLAB软件,提高了该软件解决工程实际问题的能力,进一步拓宽了处理工程测量数据和图形的工程软件。
3)该方法可适当推广,为进一步判断圆曲线道路在高差上的和缓性打下基础,可以考虑应用三角高程控制测量的方法,探究出判断圆曲线道路关键点坐标的精度。
