基于Voronoi图选点法的响应面法
2022-05-25尚昆
尚昆
(中国直升机设计研究所,江西景德镇 333001)
0.引言
在进行结构可靠性分析时,通常使用结构功能函数来表征结构响应值与变量之间的关系。对于简单的现实问题,可以通过解析解或数值分析的方式获得其可靠性指标与设计验算点。但对于复杂的结构系统,其功能函数通常为隐式的。针对这一问题,可采用蒙特卡洛法(Monte Carlo Simulation,MCS)、一阶可靠性方法(First Order Reliability Method,FORM)、二阶可靠性方法(Second Order Reliability Method,SORM)等。但此类方法计算成本较大,特别是失效概率较低的复杂结构问题。
响应面法(Response Surface Method,RSM)作为一种重要的结构可靠性分析方法,其通过简单的响应面函数来近似提到原有复杂的结构功能函数,可以极大地减少结构失效概率的计算量,提高可靠性分析效率。目前,在工程中应用较多的是由Bucher等提出的选代响应面法及其改进[1-2]。该类响应面法使用二次多项式作为响应面的形式,每次迭代响应面均由2n+1个样本点构建而成。Kim等[3]提出了向量映射法,是样本点更加接近于极限状态面,从而加快迭代。以上响应面法,在每次迭代中仅使用本次迭代出的样本点,丢失了很多样本信息。文献[4]采用加权响应面法来近似隐式极限状态,通过权函数对全部样本点进行处理后,使用全部样本点构建响应面,从而加快收敛速度,但容易导致回归矩阵病态[4]。对响应面模型贡献最大的区域为极限状态面和设计验算点周围区域,而基于最小二乘法的响应面法是一种基于全局逼近的模型,无法实现局部近似。
向量映射法以及加权响应面试图通过将样本点选择在极限状态面上以及为贡献大的区域赋予更大权重的方法解决这一问题。文献[5]用移动最小二乘法对曲线曲面进行拟合,利用了全部样本点,在每一次送代时,通过为每个拟合点赋予影响域的方式来选择合适的样本点来拟合[5]。这一方法实现了局部近似,得到了精度高的曲线曲面。
但是样本均匀程度在移动最小二乘法的拟合效果上起着重要作用[6],因此基于移动最小二乘法的影响面模型的关键就是选取均匀性好的样本。常见的实验设计方法通常只能保证本次迭代样本的均匀性,无法保证整体样本分布均匀性的质量且采样过程具有随机性,因此即使使用同一种实验设计方法进行重复试验,也可能产生不同的计算结果。Voronoi图可以在已有样本的情况下,找到距离现有样本最远位置的样本点,通过这种方法选取的样本不会产生聚集,且均匀性较好,且采样过程是确定的,消除了由样本选择的随机性导致样本均匀性质量的波动。
同时,由于响应面模型的精度和效率主要取决于设计验算点附近的近似效果。且随着迭代,响应面模型的设计验算点逐步逼近真实设计验算点,因此,应在设计验算点附近的区域内选取样本。
1.传统响应面法
响应面法的基本思想是通过简单的显式函数来近似替代真实的结构功能函数,传统响应面法使用不含交叉项的二次多项式作为响应面模型的基本函数,假设n维随机变量X=[x1,x2,…,xn],则响应面函数为:

其中,ai,bi,c为系数。

传统响应面法每次迭代只使用本次抽取的样本点,且f的取值对最终结果影响很大[7]。f值越小,则其稳定性较差,反之,则试验设计点附近近似效果难以保证。
2.改进响应面法
2.1 移动最小二乘法的基本原理
考虑在一个n维变量空间中,定义变量X=[x1,x2,…,xn],则其响应面模型可以表示为:

其中,p(X)为该响应面的基函数,本文选用仅含平方项和线性项的二次多项式作为基函数;a(X)是该基函数对应的系数向量,假设样本点个数为N(N≥2n+1),则p(X),a(X)分别表示为:

系数向量a(X)可以通过最小化样本集样本值与拟合值之间的加权误差H(X)获得,其中
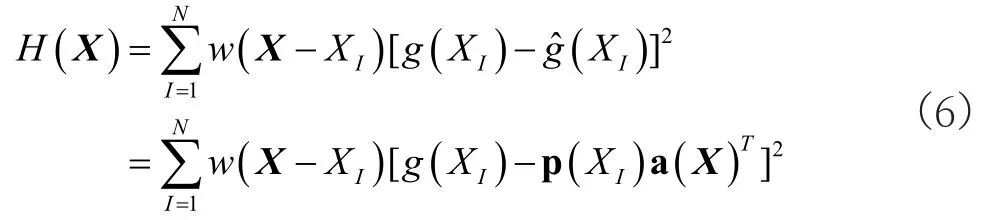
通过对上式进行最小化,即求解H(X)的极值,令∂H/∂a=0,可得系数向量

其中,g,W,P分别为

w(X-Xi)为权函数,本节仅以高斯函数为例进行展示:

式中,α为任意参数,可根据不同模型的拟合效果加以调整,本文取α=1,R为影响域半径,影响域是移动最小二乘法区别于最小二乘法最大的特征,影响域越小,其局部拟合越精确,同时影响域也应足够大,以保证该影响域内具有足够的样本点(N≥2n+1)。
2.2 基于Voronoi图的实验设计
Voronoi图是对空间平面的一种剖分,是由一组连接两相邻样点线段的重直平分线组成的连续多边形,因此该多边形的顶点为距离最近样点最远的位置。选择这些位置的样本可以有效保证空间样本的均匀程度。但由于Voronoi选点法不会在设计验算点附近聚集,导致迭代出的响应面模型熟练速度较慢。为解决这一问题本文同样选择个设计验算点的顶点作为新的样本点。
根据上述推导过程,基于Voronoi选点法和移动最小二乘法的响应面法的计算步骤如下:
步骤1:确定样本空间,选取初始样本点。在标准正态空间中,本文选取以坐标原点为抽样中心点,在坐标轴上距离抽样中心点一定距离f(f=3)的点作为初始样本点。
步骤2:将样本点代入结构功能函数g(X)中,获得其响应值,并代入式(7)中求解系数向量。
步骤4:以设计验算点作为新的抽样中心点,形成Voronoi图,以抽样中心点为样点的多边形顶点构成候选样本集SA,并在样本集SA中选取n个距离抽样中心点最远的多边形顶点构成样本集Sa。并找出样本空间中其余所有顶点构成侯选样本集SB,在候选样本集SB中选取n个距离现有样本点最远的样本作为新的样本Sb。则本次迭代的样本点由Sa、Sb以及抽样中心点构成。
重复步骤2-4直至满足下列收敛条件:

其中,ε为要求的计算精度。
3.算例验证
为了便于对本文方法进行分析和说明,本算例选取文献[7]功能函数:

式中,x1,x2相互独立且均服从标准正态分布。设置收敛条件为ε≤0.01,用一阶可靠性方法计算出的设计验算点作为参考值。其计算结果如表1所示。

表1 计算结果
通过数值算例可以看出,本文方法运算次数(计算效率)相比传统响应面法有明显提高,且试验设计点也更准确,误差小于传统响应面法。
4.结论
移动最小二乘法具有局部计算精度高的优点,但若样本集在拟合点分布不均匀时其拟合误差较大,且容易导致回归矩阵奇异,因此移动最小二乘法对样本的均匀程度要求较高。
针对现有实验设计方法存在的无法根据已有样本点进行抽样,进而导致样本在空间中分布不均匀,且抽样过程中存在随机性的问题。本文将Voronoi图选点法引入响应面模型中,通过Voronoi图的特点在感兴趣的样本空间选择出距离现有样本最远的点作为新的样本,避免样本点集中在少数区域,从而提高了空间样本的均匀程度。算例分析结果表明,本文方法选取的样本更加合理,结合移动最小二乘法有效提高了响应面法的精度和效率。
