有关全等三角形问题的易错点剖析
2022-05-25张伟
张伟
全等三角形及其应用是平面几何的重要内容之一.它涉及两个三角形的位置关系和数量关系.不少同学在求解全等三角形问题时,由于对概念、性质和判定条件的理解不清或对问题考虑不全面,往往会出现各种错误.对此,笔者对全等三角形问题中的易错点进行了归纳,以期同学们能够从中吸取经验教训,避免犯类似的错误.
错解之一:对应關系识别有误
识别全等三角形的对应关系是破解全等三角形问题的重要步骤.许多同学在解题过程中,常常因不能正确地找出全等三角形中的对应边、对应角,致使解题出错.在复杂的图形中寻找全等三角形的对应元素时,一定要将全等三角形分离出来,能重合的元素才是对应元素.
例1如图1,已知在△ABC中,∠A=70°,∠B=60°,AC=20cm;而在△DEF中,∠D=50°,∠E=60°,DE=20 cm,试问:△ABC与△DEF是否为全等三角形?请说明理由.
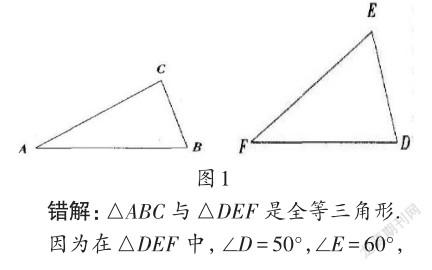
所以∠F=180°-50°-60°=70°.
又因为在△ABC中,∠A=70°,∠B=60°,
所以∠A=∠F,∠B=∠E,
又因为AC=DE=20,
所以△ABC≌△DEF.
剖析:出错的主要原因是对应关系识别有误.在△ABC中,AC是∠B的对边,在△DEF中,DE是∠F的对边,AC的对应边为DF,而不是DE,故而AC=DE这一已知条件无法作为判定△ABC与△DEF全等的条件.
正解:△ABC与△DEF不是全等三角形.
如图1所示,在△ABC中,∠B对应AC,在△DEF中,∠E对应FD,AC=DE≠FD,∠B=∠E≠∠F,由此可知△ABC与△DEF相似,但并不全等.
评注:两边对应相等,是两个三角形全等的重要条件.但相等的两边不一定就是相等两角的对边,故而只相等不对应的两边,并不能用作判定两个三角形全等的条件.
错解之二:忽略定理成立的条件
在利用全等三角形的判定定理去判定两个三角形全等时,很多同学常常忽略或篡改定理成立的条件,在解题中运用的某个条件并不是所证的两个三角形的边或内角,故而造成错解.证明三角形全等,要根据三角形全等的判定方法去寻找边与角对应相等的关系.
例2如图2所示,设∠QMN=∠1,∠QMP=∠2,∠QOP=∠3,∠QON=∠4.已知∠1=∠2,∠3=∠4,求证:MP=MN.
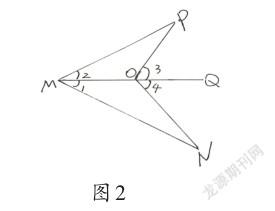
错证:在△MOP和△MON中,∠1=∠2,MO=MO,∠3=∠4,
所以在△MOP≌△MON,所以MP=MN.
剖析:上述证明之所以出错,是因为忽视了全等三角形判定定理成立的条件,解题过程利用的是三角形的边和三角形的外角,而不是三角形的内角.题目中的∠3和∠4恰好是△MOP和△MON的外角,并非内角,故而要证明△MOP≌△MON,不能直接利用∠3=∠4,但可以在此基础上进行转化,先推导出∠MOP=∠MON,再利用全等三角形判定定理去证明.
正解:因为∠3=∠4,且∠MOP,∠MON分别是∠3,∠4的补角,
所以∠MOP=∠MON.
在△MOP和△MON中,∠1=∠2,
MO=MO,∠MOP=∠MON,
所以△MOP≌△MON,
所以MP=MN.
评注:全等三角形的判定定理实质上利用的是三角形的边和三角形的内角的对应等量关系,同学们在证明时切不可忽略或随意篡改全等三角形判定定理成立的条件.
错解之三:判定方法运用不当
不少同学在判断两个三角形是否全等时,常因判定方法运用不当,导致求证错误.判定两个三角形为全等三角形的方法有角边角定理(ASA)、边角边定理(SAS)、角角边定理(AAS)、边边边定理(SSS)以及斜边、直角边(HL)定理等.同学们要牢固掌握这五种方法,切忌凭空臆造判定方法.
例3如图3,已知AC与BD相交于E,且AD=BC,∠C=∠D,求证:AC=BD.
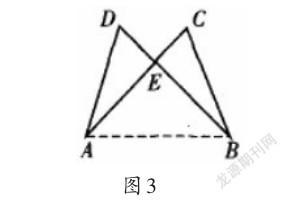
错解:连接AB .
由题意可知,在△ABD和△BAC中,
因为AD=BC,AB为公共边,∠C=∠D,
所以△ABD≌△BAC(SSA),
所以AC=BD.
剖析:上述错误在于判定定理运用不当,臆造了“边边角(SSA)”判定三角形全等.事实上,在两个三角形中,两边及其夹角对应相等的三角形是全等三角形,然而两条边和一角对应相等的两个三角形不一定是全等三角形.此题中,要证明AC=BD,只需要证明AE+EC=BE+ED即可.由已知条件∠AED=∠BEC,∠C=∠D,AD=BC,再根据“角角边AAS”判定定理,很容易得出AE=BE,DE= CE,即可推出AC=BD.
正解:在△AED和△BEC中,
因为∠AED=∠BEC,∠C=∠D,AD=BC,
所以△AED≌△BEC(AAS),
所以AE=BE,DE=CE,
即AE+EC=BE+ED.
又因为AC=AE+EC,BD=BE+ED,
所以AC=BD.
评注:用“边边角”证明三角形全等是一类常见的错误,利用两条边和一个角证明两个三角形全等时,必须强调是“两边的夹角(SAS)”,才能证明三角形全等成立.
