火箭助推器伞降回收系统建模及仿真分析

陈潇然 万寒月 王炳文 邢小军

摘要：在火箭助推器回收过程中，经过降落伞减速，系统将以稳定速度飞行，此时高空风场将成为返回过程的主要影响因素。通过牛顿-欧拉方程建立了火箭助推器-降落伞系统的六自由度模型，并在此基础上建立系统风场模型。通过数值仿真研究了火箭助推器-降落伞受风干扰及外界不确定因素扰动下的运动规律，仿真结果表明：所建模型可以精确描述风场中火箭助推器-降落伞的运动特性;风场对火箭助推器-降落伞系统的飞行轨迹和姿态角有较大影响，为后续的研究提供参考依据。

关键字：火箭助推器;降落伞;风场;动力学建模;飞行特性

一、引言

降落伞是一种可展开式气动减速装置，其产生的气动阻力可使飞行器减速到预定速度并平稳落地。目前，降落伞在越来越多的领域得到应用，如发生自然灾害或战争时，可以通过降落伞空投物资设备、武器弹药;在航空航天领域，降落伞可用于深空探测、航天器减速回收;在民生领域，同样广泛使用到定点跳伞、精准着陆等。近年来，我国航天事业发展取得了显著成绩，火箭发射活动位居世界前列[1] ，使得降落伞系统在火箭助推器回收領域受到广泛关注并成为研究热点。

火箭助推器在实施级间分离后，由于惯性作用仍处于高空高马赫飞行状态，通常速度在1马赫数以上[2] ，若不对其坠落过程施加控制，可能对落区范围内的建筑造成破坏，对地面人员及财产造成威胁。所以，应用降落伞系统对火箭助推器回收过程进行减速，成为当下迫切需要解决的一项命题。20世纪80年代起，各国运载火箭伞控回收工作取得长足发展，如美国Kistler航宇公司开展的两级运载火箭K-1的回收 ，欧洲航空局与俄罗斯合作的“阿里安5”助推器回收以及随后美国进行的“战神I-X”运载火箭试验性发射回收[3] 等。

而我国的研究起步较晚，整体研究尚处于理论到实际应用之中[4] 。国防科技大学进行了火箭助推器回收方面的数字仿真分析[5]。中国运载火箭研究院及空间机电所合作进行了运载火箭分离体安全回收方案设计及演示验证项目，相继进行了系统方案论证和缩比模型的回收试验工作[6]。

在回收过程中，火箭助推器-降落伞系统经过降落伞拉直阶段、充气阶段两个较短过程后，将以稳定速度降落飞行到预定高度。此时，风场作用将成为系统飞行运动特性的主要影响因素。然而，目前对火箭助推器回收伞降过程的研究多集中在无风作用情况下，多数未考虑该阶段风场作用对火箭助推器-降落伞系统姿态轨迹的影响，假设其平稳过渡到翼伞控制阶段。

本文根据牛顿-欧拉方程建立火箭助推器-降落伞系统的六自由度模型，在此基础上，构建组合体在风场作用下的动力学模型，仿真分析了受风干扰及外界不确定因素扰动后对系统飞行轨迹、姿态的影响，研究火箭助推器-降落伞系统实际飞行过程中的运动规律。

二、火箭助推器-降落伞系统六自由度模型

（一）建模前的定义

建立火箭助推器-降落伞系统模型前，做如下假设：

1.降落伞的气动压心位于其几何中心;

2.降落伞与火箭助推器间刚性连接;

3.降落伞完全张开;

4.平面大地。

（二）降落伞气动力和气动力矩

火箭助推器-降落伞系统在稳定飞行段主要受到气动力和重力作用，其中，气动力作用在降落伞压力中心，和降落伞的气动特性相关。

用Fn、Fz和Fa分别表示火箭助推器-降落伞系统沿ox、oy、oz方向的气动力分量，L、M、N表示气动力矩分量，（xc，yc，zc）为降落伞压心在体坐标系中的坐标，vc为降落伞压心的速度，（CA）为降落伞的阻力特征。

CT、CN对应降落伞的轴向和法向力系数，本文参考文献中降落伞气动参数辨识结果[7]，取CT = 0.7，CN为法向力系数，与降落伞的迎角α有关，关系为：CN=0.512α3-0.2652α。

（三）组合体动力学方程

根据火箭助推器-降落伞受力分析，建立用来描述系统质心三个方向线运动以及角运动的六自由度方程：

（1）

（2）

式中，火箭助推器-降落伞组合体质量m=mw+mc+mf，分别对应火箭助推器、降落伞的质量和降落伞附加质量Ixx、Iyy、Izz为系统在各轴上的转动惯量，其中，转动惯量包括降落伞转动惯量和火箭助推器转动惯量两部分，具体计算方法参考文献[11]。uc、vc、wc及pc、qc、rc表示组合体速度在体坐标系内沿x轴、y轴、z轴的速度分量和角速度分量，φc、θc、ψc为对应的姿态角。由式（1）、（2）以及系统初始状态，通过数值积分即可计算分析火箭助推器-降落伞系统稳定飞行段运动参数。

三、风场模型

为研究火箭助推器回收过程中受风影响情况，在建立组合体动力学模型之后，将风速vw在大地坐标下分解为uw，vw，ww叠加在系统空速vc上，即用uk，vk，wk代替uc，vc，wc，建立火箭助推器-降落伞系统风场模型。

四、仿真结果分析

根据火箭助推器-降落伞系统动力学方程，建立组合体的六自由度模型，分析火箭助推器-降落伞系统在稳定下降过程受风干扰及外界不确定因素扰动后的运动规律。

（一）风速影响分析

取降落伞完全充满时刻为系统稳定下降段的起始条件，初始位置（0，0，9000m），初始速度45m/s，火箭助推器-降落伞系统质量为1830kg，伞衣面积为160m^2，得到火箭助推器-降落伞系统的运动轨迹如图1所示。

由图1（a）、（b）可见，在无风情况下，火箭助推器-降落伞组合体的运动轨迹为直线，从稳定下降到翼伞打开前飞行水平距离为204m，同时下降1100m，稳定后系统水平速度为5.5m/s，垂直速度为34.76m/s，合速度为35.3 m/s。

1.水平常值风对系统运动影响

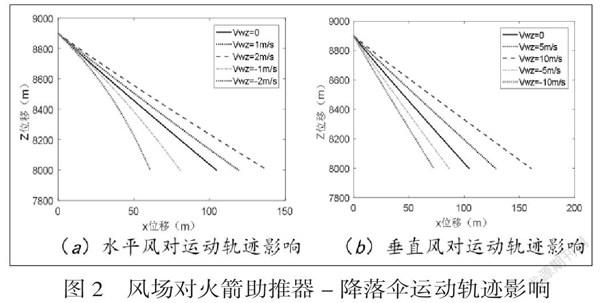
为分析风速对组合体运动情况（主要为前进距离和下降高度）的影响，将无风状态下组合体降落至指定高度的位置设定为目标点，系统运动方向及Z轴方向为正。考虑系统受到无风、常值逆风-1m/s、-2m/s和常值顺风1m/s、2m/s的情况，仿真给出了不同风速下系统运动参数情况及水平风速对运动轨迹的影响，如图2（a）所示，可以得到：

高空中的水平常值风对火箭助推器-降落伞系统的水平速度影响较大，而系统的垂直速度则不受影响。当组合体飞行过程中遇到水平逆风时，前进速度随着风速的增大而减小，逆风风速为0m/s，-1m/s及-2m/s时，所对应的前进速度分别为5.5m/s，4.6m/s及3.5m/s，垂直速度不受风速的改变而改变，仍为34.76m/s。而当组合体遇到水平顺风情况则与之相反，前进速度随风速的增大而增大。在前进距离方面，组合体逆风飞行时前进距离随风速的增大而减小，而顺风飞行时前进距离风速的增大而增大，如风速2m/s时，组合体前进距离138.1m，比无风情况增加33.4m。

2.垂直常值风对系统运动影响

考虑无风、常值逆风-5m/s、-10m/s和常值顺风5m/s、10m/s的情况，仿真给出了不同风速下系统运动参数情况及垂直风速对运动轨迹的影响，如图2（b）所示。

由图2（b）可见，当组合体遇到向上增大或向下减小的垂直风速时，系统的垂直速度随之减小，而水平速度不发生改变。比如，向上风速为0m/s，10m/s时，所对应的垂直速度分别为34.76m/s，23.64m/s，而水平速度均为5.5m/s。在前进距离方面，垂直向上的风速对组合体的运动轨迹影响较大，向上风速为5m/s、10m/s时，对应前近距离为128.8m和161m，且增幅较大。

（二）风场扰动分析

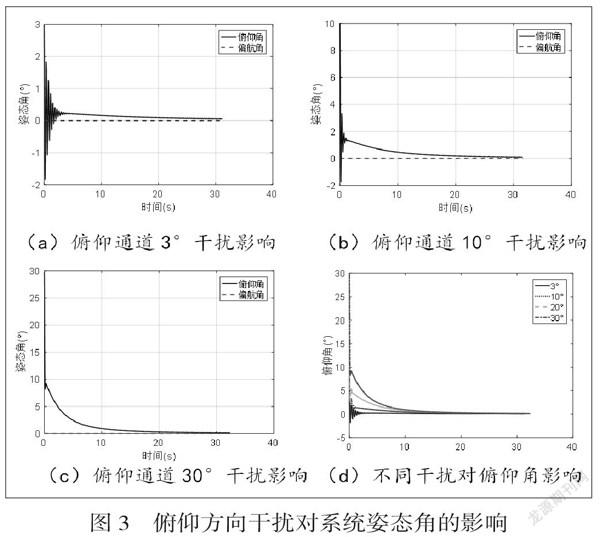
在火箭助推器减速过程中，随着降落伞开伞带来的瞬间阶跃阻力的增大，系统的姿态稳定性会受到影响，本节就系统受到不同程度风场干扰后，分析俯仰、偏航两个通道（系统绕对称轴的滚转运动可忽略）的扰动响应情况。分别给火箭助推器-降落伞组合体俯仰、偏航通道3°、10°、30°的风场扰动，得到系统姿态变化情况如图3所示。

图3（d）是火箭助推器-降落伞系统受到俯仰通道不同程度扰动后，其俯仰角、偏航角的响应情况。由图3 （a）～3（c）可见，在稳定下降段，当系统分别受到俯仰通道3°、10°和30°干扰后，俯仰角的振荡状态均会逐渐减弱，并最终趋向于0°的稳定状态;而偏航角不会受到俯仰通道干扰的影响，一直维持在0°状态。可见垂直方向的扰动对组合体的干扰程度较小，系统最终会回到稳定状态。

图4是火箭助推器-降落伞系统受到偏航通道不同程度扰动后，其俯仰角、偏航角的响应情况。由仿真结果可见，俯仰角受到偏航通道3°干扰后，将以正弦函数的形式进行周期性运动，而偏航角受到小扰动后，会以振荡衰减的形式运动;当系统受到30°的大扰动时，俯仰角会逐渐发散，最终维持在等幅周期性振动状态波动。而偏航角响应与之相反，先以衰减形式振荡，最后以同等周期维持在等幅振动状态波动。由图4 （b）可见，系统稳定后，俯仰角与偏航角在波动过程呈现一定的相位差，可见系统整体将以圆锥运动的形式存在。

五、结束语

（一）数值仿真实验结果表明，本文建立的火箭助推器-降落伞的动力学模型及风场模型，能够准确反映系统在风场作用下的飞行特性。

（二）高空中的水平常值风对火箭助推器-降落伞系统的水平速度影响较大，而系统的垂直速度则不受影响;同样，垂直常值风只对系统的垂直速度产生较大影响。

（三）当火箭助推器-降落伞系统受到俯仰通道的风场扰动后，俯仰角均以振荡衰减的形式运动，并最终趋向于0°的稳定状态，而偏航角则不受影响，一直维持在0°状态。

（四）当系统受到偏航通道的风场扰动后，若干扰影响较小，俯仰角将以小幅度进行等幅振荡，偏航角将以振荡收敛的形式波动;若干扰影响较大，俯仰角运动呈现发散趋势并最终维持在等幅振动状态，而偏航角运动先出现衰减趋势，最终以一定相位差呈现与俯仰角相同运动状态，此时火箭助推器-降落伞系统呈现为圆锥运动形式。

作者单位：陈潇然    万寒月    王炳文    西安航空工业计算技术研究所

邢小军    西北工业大学

陈潇然（1995—），男，陕西西安，硕士研究生，助理工程师，主要研究方向为计算机应用。

参  考  文  献

[1] 曲向芳. 2020成就斐然 2021精彩纷呈——《中国航天科技活动蓝皮书（2020年）》[J]. 卫星应用， 2021（3）：2.

[2] BOS M， OFFERMAN J. Post-flight 503 evaluation of the Ariane-5 booster recovery system[C]. Aerodynamic Decelerator Systems Technology Conference. 2013.

[3] TARTABINI P， STARR B， GUMBERT C， et al. Ares IX separation and reentry trajectory analyses[C]. AIAA Atmospheric Flight Mechanics Conference. 2011： 6462.

[4] 馮韶伟.国外运载火箭可重复使用关键技术综述[J].导弹与航天运载技术，2014（5） ： 82-86.

[5] 江琳. 火箭助推器回收系统初步设计及仿真研究[D]. 国防科学技术大学， 2009.

[6] 张兴宇. 翼伞热气球空投试验技术概论[C]. 第二届进入、减速、着陆（EDL）技术全国学术会议，南京，2014.

[7] 程文科.一般降落伞-载荷系统动力学及其稳定性研究[D].长沙：国防科技大学博士学位论文，2000.