基于稀疏表示的阵列声波测井仪数据无损压缩传输方法
2022-05-24尹时松李波宏庄献华李江山
李 明,尹时松,张 宁,李波宏,庄献华,李江山
(中国石油集团测井有限公司华北分公司,河北 任丘 062552)
作为一种重要的成像测井仪器,交叉多极子阵列声波测井仪[1]将单极发射、接收阵列和偶极发射、接收阵列交叉组合;其中,单极子阵列包括关于井轴对称、全方位的2个发射换能器和8个接收换能器,偶极子阵列包含正交放置的2个发射换能器和16个接收换能器。各个接收换能器记录声源发射后一定时间段内的声波波列,通过时间-慢度相关方法[2]计算地层的纵波、横波和斯通利波慢度,可用于识别岩性、计算岩石力学参数、识别气层和裂缝,而由偶极阵列可得到地层快、慢横波速度和方位,进行地层各向异性分析,已广泛应用于碳酸盐岩油气层[3]、煤层气[4]和致密砂岩气层[5]的勘探开发。
阵列声波测井仪声波发射、接收换能器众多,且采集声波波列,因此仪器上传地面的数据量很大。目前仪器仅有约42 kbit/s的最大电缆上传速率,一旦提高仪器的测井速度,传输队列中当前地层的测量数据在未上传到地面系统的情况下,就会被新地层的测量数据覆盖。因此,在井下仪器采用无损数据压缩上传是在采集数据不失真的同时,增加传输带宽、提升仪器测井时效的有效方法。
目前主流的测井数据无损压缩方法是LZW(Lempel Ziv Welch,蓝波-立夫-卫曲)算法[6-9],但LZW算法在编解码过程中,需要存储编码字典,因此当非平缓变化数据流的信息冗余较少时,压缩率较低;文献[10]针对阵列声波测井仪提出一种预测编码方法,但没有考虑声波波列的数值时序分布规律,预测误差编码码位较长,导致预测器性能不佳;文献[11]提出一种基于BWT(Burrows-Wheeler Transform,伯罗斯-惠勒变换)和PPM(Prediction with Partial Matching,局部匹配预测)算法的阵列声波数据无损压缩传输方法,虽然考虑了声波波列中数据分布规律,但算法复杂程度较高,要求实际应用中使用高性能的DSP硬件,且压缩率最高只有51%,不能达到当前测井作业效率指标。
以上的压缩方法都是基于传统的信息熵减少理论,将声波波列数据尽可能地转换为平缓变化的数据流。如果从信号处理的角度考虑,将声波波列从时间域转换到某一变换域,且在该变换域,声波波列只需极少的量值表征,那么井下上传这些表征量值到地面系统,反变换后,就可恢复原始声波波列。因此,从信号稀疏表示的角度出发,通过稀疏变换将声波波列变换到其稀疏域。选择恰当的稀疏变换矩阵,可使稀疏表示系数中非零元素个数远小于波列长度。这里,采用K-SVD(K-means Singular Value Decomposition,K均值奇异值分解)算法,通过历史声波波列数据训练稀疏变换矩阵。数据上传时,将非零稀疏表示系数和重构波列与原始波列的误差进行压缩编码上传。在地面系统采用相同的稀疏变换矩阵进行反变换,再叠加误差信息,恢复原始波列。通过HB油田阵列声波仿真实验、实测数据压缩率比对和实际作业的应用测试,验证方法在提升数据压缩率和提高测井作业时效方面的有效性。方法的设计和开发有望提升阵列声波测井的施工速度,为油田勘探的提质提效提供有力的技术支撑。
1 阵列声波信号采集和传输原理
交叉多极子阵列声波测井仪在一个深度点记录12道单极子波列和32道偶极波列,包括8道单极子声源T1发射,8个接收器采集的全波波列、4道单极子声源T2发射,前4个接收器采集的全波波列和32道正交的两个偶极子声源交替发射,交叉放置的16个偶极接收器采集的偶极波列。
表1给出了GBG1井阵列声波测量数据在一个深度点的存储格式。由表1可以看到,单极子声源T1发射采集的8道全波波列,存储在曲线TFWV10中,总采样点数为5376,每道波列点数则为672。同样地,单极子声源T2发射采集的4道全波波列,存储在曲线TNWV10中,总采样点数为832,每道波列点数则为208。而TXXWV10、TXYWV10、TYXWV10和TYYWV10则分别为采集的4个偶极分量,每个分量存储8道全波波列,每道波列采样点数为400。

表1 GBG1井阵列声波测量数据存储格式
图1给出了GBG1井TXYWV10曲线在3759.94 m深度处,采集的8道偶极波列。可以看到,各道全波波列具有较高的相似性。
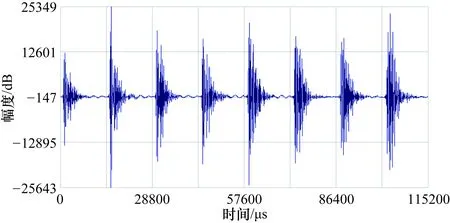
图1 GBG1井3759.94 m处 TXYWV10波形
如图2所示,阵列声波信号的数据上传是通过遥测传输短节实现的。仪器采集的各道声波全波列(一维时间信号)在井下仪器总线控制器的作用下,通过井下仪器总线,传入遥测短节内进行缓存,形成上行数据帧。对数据帧进行PCM编码后,转换为模拟信号,经低通滤波和差分驱动,送入与传输电缆相连的模式变压器,产生电缆中电压的高低变化。地面系统在检测到电缆电压的变化后,经过信号滤波处理和模数转换,以及PCM解码,可接收到上传的阵列声波采集数据。由于高频信号经测井电缆长距离传输后,幅度大幅衰减且信号严重失真,造成测井电缆传输带宽有限。以阵列声波数据传输为例,由表1可知波列每个采样点的值为2 B长度的有符号SHORT型,计算一个深度点的阵列声波采样数据帧大小至少为37.125 KB,电缆上传速率为41.66 kbit/s,则数据传输时间约为0.8911 s,加上声源发射和阵列接收换能器采样时间约为0.2 s,在不计入其他一维、二维采集数据的情况下,一次采集加数据上传的时间至少为1.0911 s,而阵列声波的深度采样间隔为0.1524 m,可知仪器在单位深度地层的工作时长最小约为7.16 s。因此,在数据上传前,对采集数据进行有效压缩编码,可大幅减少数据上传时间,变相增加单位时间内传输的数据量和电缆上传带宽,进而减小仪器在单位深度地层的工作时长。

图2 阵列声波测井仪数据传输原理框图
2 阵列声波采集数据无损压缩方法
2.1 信号稀疏表示原理
由信号稀疏表示理论可知,如果原始信号是稀疏的,则可以将其用一稀疏正交基和非零个数远小于信号序列长度的稀疏系数序列线性组合表示,即稀疏变换[12];而作为稀疏变换矩阵的稀疏正交基,称为稀疏字典,可拓展为超完备的冗余字典。对原始信号f进行稀疏变换:
α=Df
(1)
式中:f∈RN×1为N个采样点的等间隔采样原始信号;D∈RM×N为稀疏变换矩阵;α∈RM×1为f进行稀疏变换的稀疏表示系数,如果M=N,则D为稀疏字典;如果M≫N,则D为超完备冗余字典。反变换有f=DHα,DH为D的共轭转置阵,满足DHD=1。
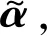
(2)

2.2 基于稀疏表示的声波全波列数据压缩方法
基于稀疏表示的声波全波列数据压缩方法原理如图3所示。
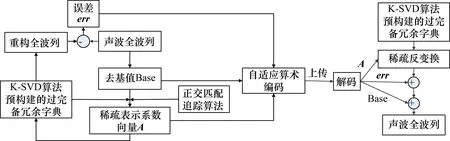
图3 声波全波列数据无损压缩方法原理框图
首先,提取一道的声波全波列数据,去除基值后,根据采用K-SVD算法预先构建的过完备冗余字典B和正交匹配追踪算法,计算稀疏表示系数向量A,对向量A中的数值取整后,再根据稀疏反变换,重构波列,得到原始波列与重构波列的误差向量err。将取整后的向量A和误差向量err中的非零值、索引和基值Base整合,形成二进制数据流,采用自适应算术编码后上传。在地面系统,根据解码后的稀疏表示系数和字典B进行稀疏反变换,得到波列估计值,再加上解码后的误差和基值,就可以完全恢复出原始的声波全波列。由于原始波列值为16位整型数,因此向量A和误差向量err中的非零值和索引值同样为16位整型。
算术编码是一种信息保持型编码,无需向LZW算法传送编码字典,因此压缩率有了明显提升。算术编码符合概率匹配原则:出现概率较大的符号压缩为较短的码字,出现概率较小的符号取较长码字。自适应算术编码根据编码时符号出现的频繁程度动态修改信源符号的概率。当出现某个符号在整个符号流中全局概率较小,但在符号流某一位置集中分布的情况时,宜采用自适应编码;由于符号出现的概率随着符号输入不断变化,输入相同符号数越多,该符号的概率被更新得越大,则该符号压缩后的码字要明显小于需要遍历的整个符号流,统计每个符号全局概率的固定模式算术编码。因此,采用编码过程中动态估计字符概率的自适应算术编码不仅在压缩算法时效上优势明显,而且压缩率也优于固定模式编码。
2.3 基于K-SVD的稀疏变换矩阵训练方法
信号的稀疏度与超完备冗余字典(稀疏变换矩阵)密切相关,选用符合声波波列特征的稀疏变换矩阵,可使声波波列在该稀疏变换矩阵下表示更稀疏。因此,采用K-SVD算法[15],以历史多道声波全波列为训练数据,预构建更符合声波波列特征的过完备冗余字典,可在提高声波波列稀疏度的基础上,进一步提升声波波列的重构精度,减少误差向量非零值数目,从而使编码数据量更小。
稀疏变换矩阵D∈RN×L(L>N),矩阵中列向量为字典原子,训练数据集X∈RN×S,X中的列向量即为一道训练用的声波全波列数据,其中L为字典原子个数,S为训练用声波全波列道数。训练过程中稀疏表示系数向量集为Γ∈RL×S。K-SVD算法的目标函数为

(3)
式中:γi为向量集Γ中第i个列向量;K为稀疏表示系数向量中非零分量个数的最大值。K-SVD算法的训练为一个迭代过程,首先给定初始矩阵D,采用正交匹配追踪算法求解训练数据集X的稀疏表示系数矩阵Γ;再根据Γ,更新矩阵D。重复进行稀疏表示系数矩阵求解和稀疏变换矩阵更新两个步骤,直至满足式(3)的迭代条件。稀疏变换矩阵需要逐一更新矩阵D中的列。假设更新D中的第j个列向量dj,计算去掉该列代表的原子成分在所有S个训练样本中造成的误差

Ej=UΔVT
式中:U为N×N维矩阵;V为S×S维矩阵;U和V是酉矩阵,与本身转置矩阵相乘等于单位阵;Δ为N×S维矩阵,其主对角线上的元素为奇异值,且除主对角线上的元素以外全为零值。更新dj为U的第1列,计算V的第1列和Δ(1,1)的乘积,更新矩阵Γ中与列向量dj对应的第j行中非零元素值。
3 实验结果分析和现场测试
3.1 仿真实验结果和分析
在仿真实验中采用COMSOL软件,模拟阵列声波仪器分别在快速地层(花岗岩)、标准地层(砂岩)和慢速地层(泥岩)的阵列声波单极子接收换能器响应。其中,模拟仪器源距为3.0 m,接收换能器间距为0.15 m,声源采用中心频率为10 kHz的Ricker子波。图4给出了快速地层中仪器8个接收换能器响应波形。

图4 快速地层中8个接收换能器响应波形
如图4所示,最上部的虚线波形为声源发射波形,源距3~4 m处从上至下分别为8道接收换能器波形。实验中,共模拟3种地层接收波形176道,采用175道全波列波形构建K-SVD算法的训练样本集。初始过完备冗余字典采用DCT矩阵,原子数设为128,训练稀疏度上限为50,训练迭代次数为100。图5和图6分别给出了1道未参与训练的声波波列采用正交匹配追踪算法在训练后冗余字典和原始Hadamard字典上的重构波形、稀疏表示系数和与原始波列的误差。
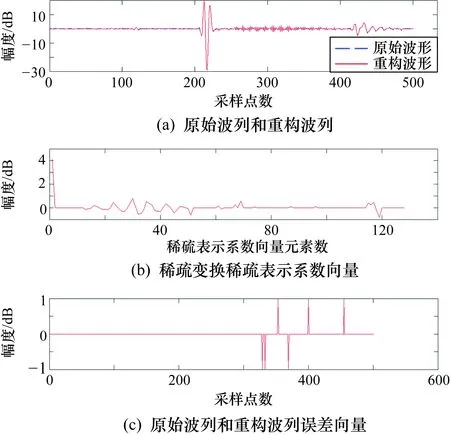
图5 仿真实验训练后冗余字典上的波列重构结果

图6 仿真实验原始Hadamard字典上的波列重构结果
这里,换能器接收波列长度为501,原始Hadamard字典的原子数为512。由图5和图6可以看到,重构波列和原始波列基本一致,但训练后冗余字典上的波列稀疏度为49,明显优于原始Hadamard字典上的波列稀疏度398。由于Hadamard字典的原子数大于K-SVD算法的过完备冗余字典原子数,因此原始Hadamard字典上的波列误差向量为0,优于训练后冗余字典上的误差向量。模拟数据压缩过程,一道原始波列为501×2 B,而经稀疏变换后,稀疏表示系数的非零值与索引值占49×4 B,加上非零误差值和索引的6×4 B,再加上波形基值2 B和标准化用到的波形最大和最小值4 B,共226 B,不考虑二进制数据流最后的自适应算术编码,则一道原始波列的最小压缩率可达到77.45%。仿真实验验证了采用K-SVD算法训练冗余字典的有效性。
3.2 实际测井数据实验结果和分析
本文采用GBG1井TFWV10曲线中4000~4038 m深度范围内的2000道声波全波列数据构建K-SVD算法的训练样本集,初始过完备冗余字典采用Hadamard矩阵,原子数设为1024,训练稀疏度上限为50,训练迭代次数为100。图7给出了该训练样本集上的迭代误差,这里对每个训练样本进行数据标准化,范围为[-1,1]。由图7可以看到,在保证声波全波列稀疏变换稀疏度的情况下,随着字典更新次数的增加,算法的均方根误差逐步减少,说明了K-SVD算法的收敛性。
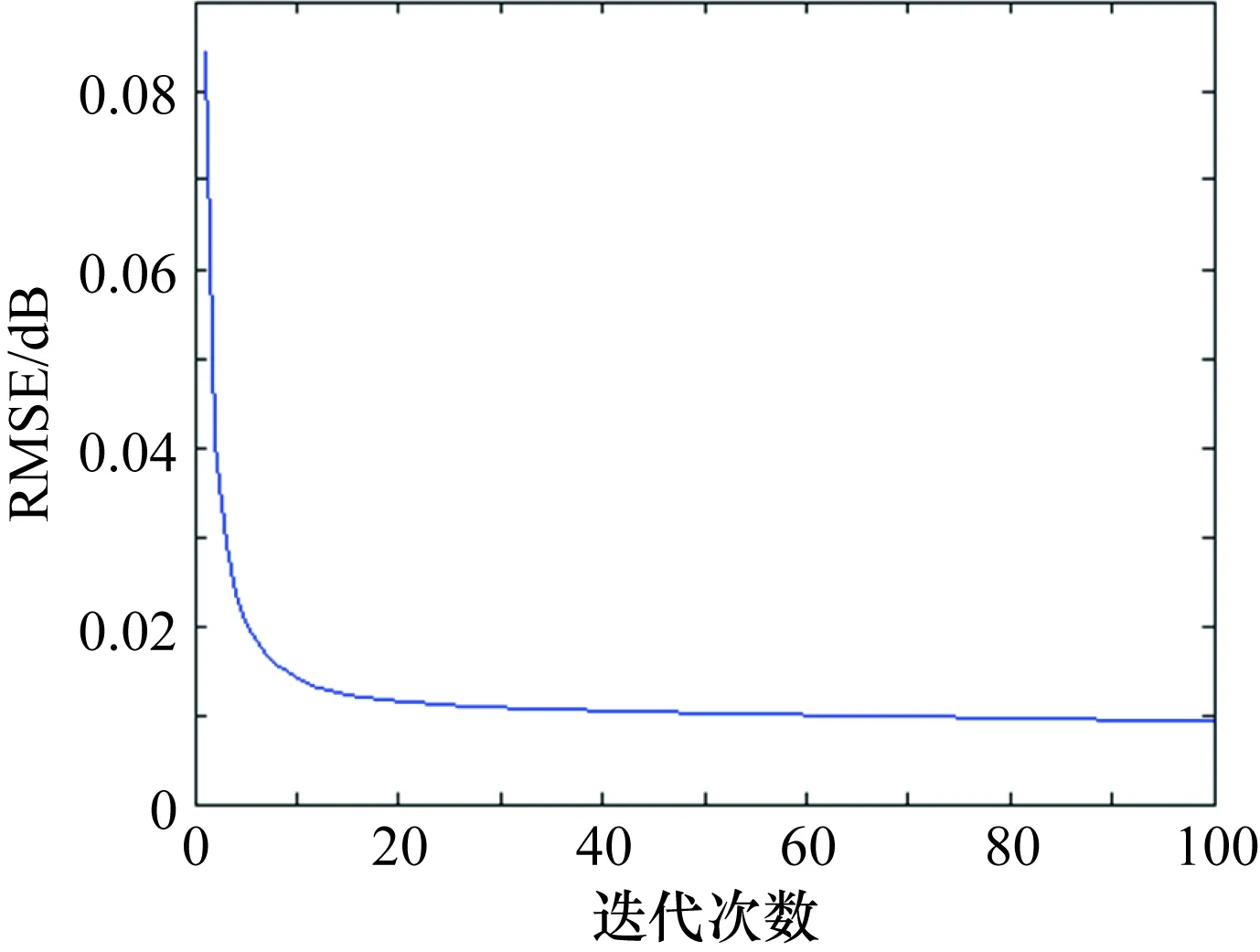
图7 K-SVD算法迭代误差
随机提取GBG1井TFWV10曲线中在训练用全波波形数据深度范围外的一道声波波列,进行数据无损压缩算法实验,验证K-SVD算法的有效性。图8和图9分别给出了该声波波列采用正交匹配追踪算法在训练后冗余字典和原始Hadamard字典上的重构波形、稀疏表示系数和与原始波列的误差。
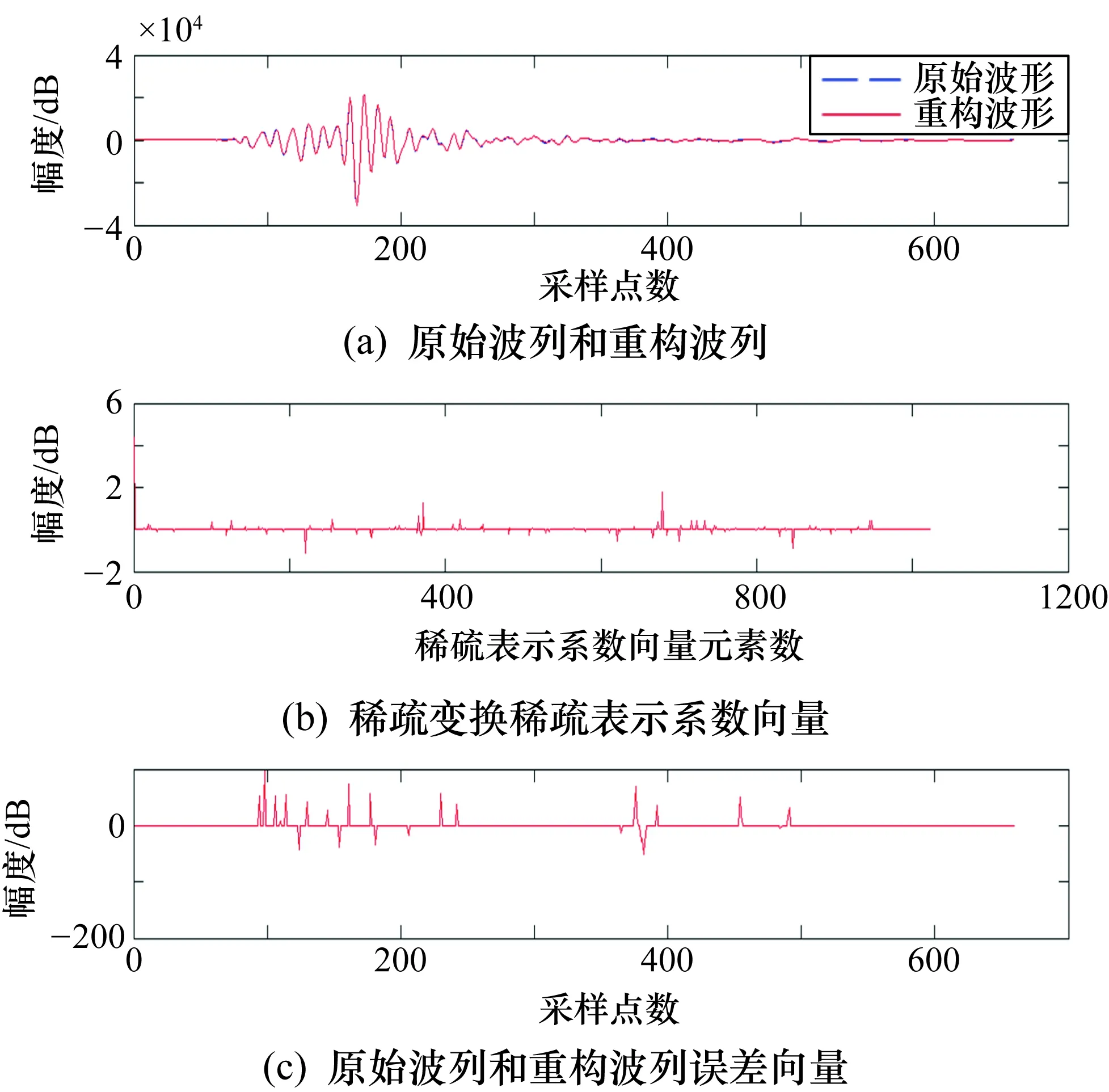
图8 训练后冗余字典上的波列重构结果

图9 原始Hadamard字典上的波列重构结果
由图8和图9可以看到,在两个冗余字典上的重构波列与原始波列基本一致,原始波列和重构波列的误差向量(图8(c)和图9(c))也验证了这一点,统计平均误差分别为0.98%和1.65%;虽然两个误差近似,但比较图8(b)和图9(b)的稀疏表示系数向量,发现在训练后冗余字典上的稀疏度明显优于原始Hadamard字典;在训练后冗余字典上的稀疏表示系数向量中非零值个数为94,而在原始Hadamard字典上的相应值为444,验证了笔者提出的无损压缩算法中对于冗余字典进行预训练步骤的必要性和有效性。模拟数据压缩过程,一道原始波列为660×2 B,而经稀疏变换后,稀疏表示系数的非零值与索引值占94×4 B,加上非零误差值和索引的37×4 B,再加上波形基值2 B和标准化用到的波形最大和最小值4 B,共530 B,不考虑二进制数据流最后的自适应算术编码,则一道原始波列的最小压缩率可达到59.85%。
针对HB油田FY1井等3口井的实测阵列声波数据,比较本算法与LZW算法、算术编码和文献[11]算法的数据压缩率,结果如表2所示。其中,算法分别针对TFWV10、TNWV10两种单极子波列和偶极接收波列,训练3种过完备冗余字典。
由表2可以看到,笔者算法的压缩率在不同数据类型上是最高的,较文献[11]算法的压缩率平均提升了约17.3%。其中,随着数据文件变大,LZW算法的压缩率有所提升,这是由于数据流中重复字符串的增多,使得字典中对应字符串编码缩短导致的。对于笔者算法,可以看到,在TNWV10数据上的压缩率略优于在TFWV10和偶极波列数据上的压缩率,这是由于TNWV10数据的全波波列长度小于256,因此在压缩时,误差的索引值只占用1 B,导致码流长度减少,压缩率增加。同时,P273井4种方法的压缩率较其他两口井在整体上有明显提升。经该井实验数据研究发现,测量井段对应地层中出现各向异性极弱的大段泥岩层,使得单极子接收波列和偶极子接收波列各道全波波列具有高度相似性,则LZW算法构造的编码字典大幅度减小,算术编码由于字符出现概率增大,编码码字缩短,导致两种算法的压缩率明显增加。由于二进制码流中,字符变化的规律性增强,也使得文献[11]算法的压缩率增加。对于笔者算法,波列的高度相似性导致训练的冗余字典更能表征波列特征,使得压缩时稀疏变换的稀疏度和重构精度增加,压缩编码长度进一步降低。
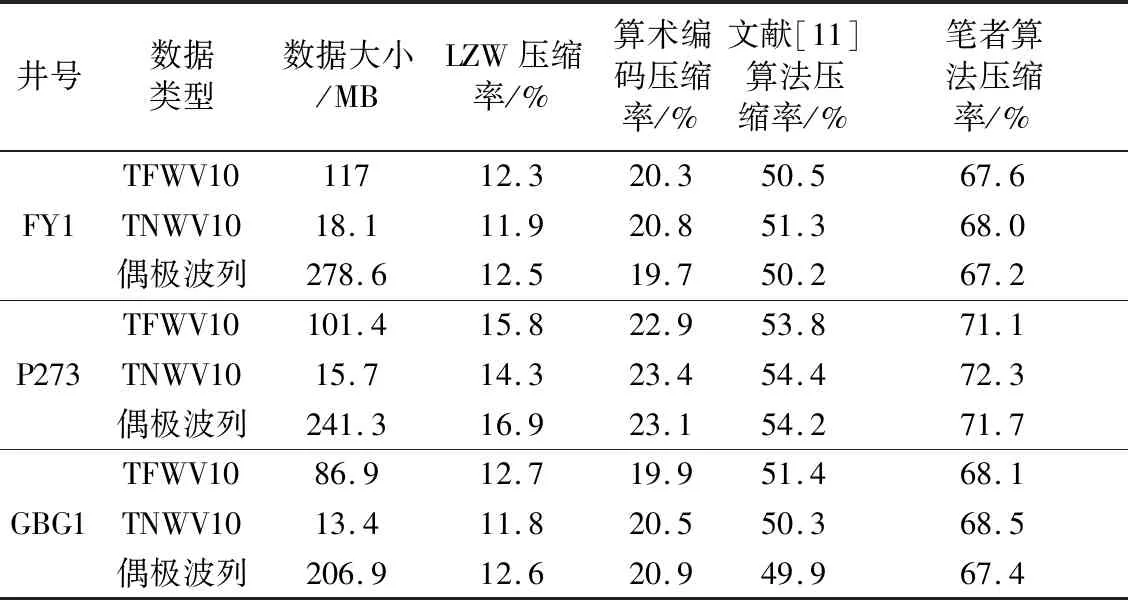
表2 算法压缩率实验结果
3.3 实际作业应用测试
重新设计的SL6680型阵列声波测井仪,应用无损压缩传输方法在HB油田GuGu8井等测井作业井眼环境较好的4口井进行了阵列声波实际作业应用测试。在应用测试过程中,对于同一口井分别采用原有的SL6680型仪器和新系统进行测井时效对比测试,结果如表3所示。
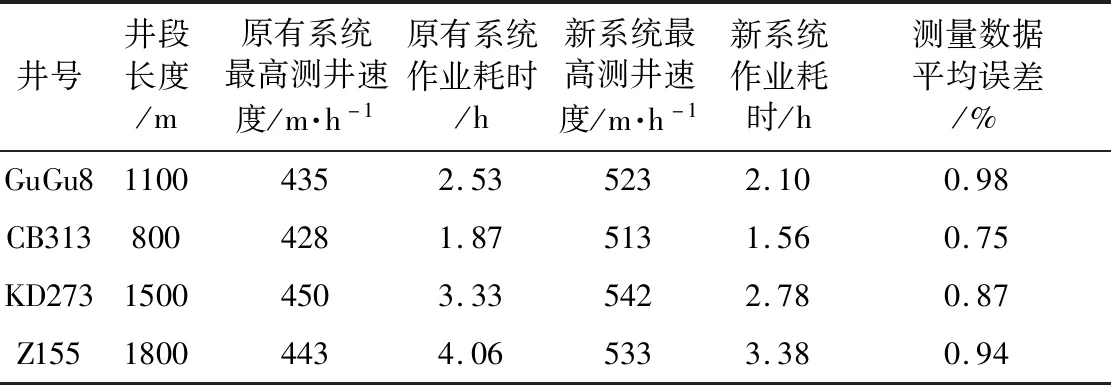
表3 测井时效对比
由表3可以看出,原有仪器和新系统的测量数据平均误差在测井重复测量标准规定的数据误差范围内,说明两者的测量数据几乎相同。在这种情况下,新系统的最高测井速度整体高于原有仪器,测井作业耗时大幅度缩短。经数据统计计算,新系统的测井效率较原有仪器平均提升了约20.2%。
4 结束语
针对阵列声波测井仪器,对采集的多道单极子和偶极子全波波列,采用基于信号稀疏表示的数据无损压缩传输算法,在数据传输带宽受限的情况下,有效提升单位时间内的上传信息量,最终提高了测井时效,使阵列声波测井仪器在保证采集数据不失真的条件下,满足油田勘探提质提效的形势需求。
