有向路径下的一类多智能体系统的能控性分析
2022-05-24张志伟纪志坚
张志伟,纪志坚
(青岛大学 a.自动化学院;b.山东省工业控制技术重点实验室,山东 青岛 266071)
0 引言
近些年,随着计算机网络技术、通信技术的日益发展,系统正逐渐从单一的传统模式演化成智能化的新型模式。智能体系统的发展也是如此,由于单个智能体解决问题的能力十分有限,通过智能体之间的相互联系,彼此协调可以解决超过单个智能体能力之外更复杂的问题,这也就形成了多智能体系统。多智能体系统具有诸多显著优势,目前已经在编队控制[1-3],能控性[4-7],能观性[8-10],一致性[11-13]等方面得到了广泛研究。
在当前世界背景下,普遍受到国内外学者关注的一个问题是系统的能控性问题,能控性是现代控制理论的一个基本概念,是对系统进行研究和分析的基础。有关能控性的研究最早可以追溯到20世纪60年代,由Kalman提出[14-15]。之后学者研究发现将能控性的概念扩展到多智能体系统之中是非常有必要的。多智能体系统的能控性是指选定部分节点作为领导者(leader)施加外部控制输入,通过系统内部个体之间的相互连接关系,可以使跟随者(follower)由任意初始状态转移到所期望的状态。多智能体系统能控性的这一概念首先是在2004年由Tanner提出,同时他还提出了一种基于leader-follower结构(领导者—跟随者结构)的网络模型[16]。在这一结构模型下,多智能体系统能控性的研究得到了进一步的发展。从代数角度出发,Ji等[17]在leader-follower结构下得到了系统能控的充分必要条件是Lf和L不共享特征值。Ji Z等[18]得到了一个基于特征值的系统能控的充分必要条件,即对应领导者位置的特征向量的元素不为0。从图论刻画的角度出发,文献[17]首次提出了等价划分的概念,此后文献[19-21]利用等价划分对不同拓扑条件下的多智能体系统的能控性进行了分析。除此之外,特殊拓扑的能控性研究也一直都是学者们关注的热点。Rahmani等[22]通过对无向路图的研究发现了研究特殊拓扑结构的能控性具有重要意义。Palangeli等[23]进行了进一步研究,得到了无向环图拓扑下多智能体系统能控的相关结论。2018年Liu等[24]综合研究了无向路图和环图下多智能体系统的能控性问题,提出了使系统能控时领导者位置的选取方式。文献[25]基于无向路图和环图研究了无向符号条件下多智能体系统能控性保持问题。
可以看出,上面有关系统能控性的研究主要是在无向无符号拓扑下进行的,即个体之间的信息传递都是双向的,且个体之间的联系权重都为正值,而有向符号拓扑条件下多智能体系统能控性的研究成果相对较少。有向符号条件下系统Laplacian矩阵区别于无向无符号图的地方主要是矩阵不再是实对称矩阵,且矩阵的行和不再一定为零。基于以上两点,许多无向无符号拓扑条件下的性质将不再适用,这也给研究有向符号拓扑条件下多智能体系统的能控性带来了困难和挑战。
本文的贡献主要包含以下3个方面:1)基于有向符号拓扑条件下的leader-follower结构模型,研究发现该模型下增加或删除网络中特定的一类边对于系统的能控性没有影响。2)从特殊拓扑能控性的角度出发,得到了有向路径拓扑下系统单领导者能控的领导者位置的选取方式。在此基础上进一步发现在有向路径中增加逆向边不改变系统的能控性,而这一结果并不适用于增加顺向边的情况,有向路径增加顺向边时系统的能控性取决于跟随者节点中是否存在非平凡胞腔。3)基于上述有向拓扑中特定连接不改变系统能控性的特点以及使得特殊拓扑能控的领导者位置的选取方式,给出了一个有向符号条件下能控复杂拓扑的构造方式。
1 预备知识
将一个包含n个智能体的多智能体系统表示为G=(V,E,A),其中,V={v1,…,vn}表示节点集,E⊆V×V表示边集,A=(aij)∈Rn×n表示邻接矩阵。有向边(vi,vj)∈E表示存在一条从vi→vj的有向边,个体之间的连接关系通过邻接矩阵A∈Rn×n来表示,其中如果(vi,vj)∈E,那么aij≠0,否则aij=0。本文不考虑存在自环的情况。

可得

(1)
假定包含n个个体的节点集V可以分为一个领导者集Vl∈V和一个跟随者集Vf∈V,且Vl∪Vf=V,因此便形成了一个经典的leader-follower结构下的网络模型。不失一般性,假定前m个个体形成跟随者集Vf={v1,…,vm},其它个体形成领导者集Vl={vm+1,…,vn}。则上述的Laplacian矩阵可以划分为
(2)
其中,Lf∈Rm×m,Lfl∈Rm×(n-m),Llf∈R(n-m)×m,Ll∈R(n-m)×(n-m)。基于式(1)和(2),可得
对于跟随者来说
(3)
在leader-follower结构中,领导者通过直接接收外部控制信号受到外部信号的控制,又因为领导者是一阶积分器系统,因此领导者是必可控的。
定义1 leader-follower结构下系统能控性假定领导者接受外部控制信号后是必能控的,leader-follower结构下系统能控的含义是系统中跟随者的状态xf(t)可以从任意初始状态到达期望的状态。
定义2m-领导者能控当使得多智能体系统能控时所选定的领导者的最小数量为m时,称系统是m-领导者能控。特别地,当m=1时,若多智能体系统是能控的,此时称系统是单领导者能控。
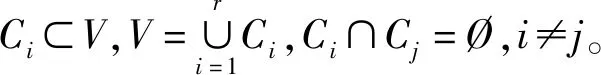
在leader-follower结构下,为判断系统的能控性,给出如下所示系统的能控性判据。
引理1 能控性判据[26]对于式(3)所示的多智能体系统,以下说法是等价的。
1)式(3)所示的多智能体系统在leader-follower结构下是能控的。
3)矩阵[sI-Lf,Lfl],s∈C或[λiI-Lf,Lfl]是满秩的,其中C表示复数域,λi(i=1,…,m)表示对应矩阵Lf的特征值。

从定义1可以看出,不同领导者的选取会使得系统的能控性不同,这也说明有向符号图下使得系统能控的领导者的选取并非任意的。
2 leader-follower结构下系统能控性的图论表征
命题1给定一个有向符号拓扑图G,其中跟随者动力学如式(3)所示,则leader-follower结构下系统的能控性不受领导者和领导者之间以及跟随者指向领导者的连接关系的变化影响。
证明:leader-follower结构下系统的能控性仅取决于Laplacian矩阵L分块中的Lf和Lfl,而不受矩阵Ll和矩阵Llf的影响。在图G中,若改变领导者与领导者之间的连接关系和从跟随者指向领导者的连接关系,矩阵Lf和矩阵Lfl都保持不变,因此leader-follower结构下系统的能控性不变。
命题1说明了单个拓扑图中连接关系出现上述两种情况时系统的能控性不变,不同拓扑图之间增加上述两种连接关系会给系统的能控性带来的影响,我们在命题2中进行论证。
考虑leader-follower结构下的n个有向符号图Gi=(Vi,Ei,Ai),i=1,…,n,其中Gi有一个跟随者集合Vfi={v1,…,vmi}和一个领导者集合Vli={vmi+1,…,vni},且Vfi∪Vli=Vi,Vfi∩Vli=φ,其中子图Gi中跟随者和领导者节点的个数分别为mi和ni-mi,Ei和Ai分别表示子图Gi的边集和邻接矩阵。
命题2给定一系列能控的有向符号图Gi,i=1,…,n,分别都是能控的,且个体状态按照邻居协议进行更新。若图G=(V,E,A)按照如下的规则进行构造,其能控性可以保持:
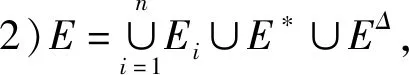
3)A表示图G中个体之间连接关系的邻接矩阵,其中Alifj和Alilj分别表示图G的邻接矩阵中对应从子图Gj中的跟随者指向子图Gi中领导者的连接部分以及从对应子图Gj中的领导者指向子图Gi中的领导者的连接部分,i,j=1,2,…,n,且i≠j。

命题2提供了一个通过能控有向拓扑子图构造复杂有向能控拓扑图的方法,除此之外,也给出了一个保证拓扑图能控的领导者位置选取方式。例如,如果一个给定拓扑图可以分为多个拓扑子图,只要在每个拓扑子图中选择保证每个子图能控的领导者,且不同子图间通过各自的领导者之间的有向边或者跟随者指向领导者的有向边建立连接关系,便可以构成一个更复杂的有向拓扑图,此时该拓扑图在原有领导者位置的选取下仍然是能控的。
3 基于有向符号路径下的一类拓扑的能控性分析
本节研究使得给定特殊有向符号拓扑能控的充分条件。有向路径作为有向拓扑里面最基础且最简单的拓扑结构,本文首先将对它的能控性问题进行分析研究,进而研究更复杂结构的能控性问题。
3.1 有向符号路径的能控性
假定一个由n+1个节点构成的有向路径图,为了便于后面的研究,将初始节点编号为n+1,并依次将初始节点后面的子节点从1到n进行编号。
定理1对于有向符号路径图G,如果选择路径中的初始节点为领导者,那么它对应的多智能体系统是单领导者能控的。
证明:将n+1个节点构成的有向符号路径的Laplacian矩阵按照式(2)的分块形式写作
其中,Lf∈Rn×n,Lfl∈Rn×(n-1)。构造矩阵[λI-Lf,Lfl]∈Rn×(n+1)如下:
该矩阵是n×(n+1)阶的,取该矩阵的前n-1列及最后一列元素构成一个新矩阵Hp∈Rn×n。利用矩阵的初等列变换计算矩阵Hp的行列式
在有向符号路径图中,存在从vn+1到v1,v1到v2,v2到v3,…,vn-1到vn的有向边,即系统中存在这些个体之间的信息传递,aij≠0。即|Hp|=(-1)na1na21a32…an,n-1≠0,矩阵Hp可逆且满秩,rank(Hp)=n。由于矩阵Hp是通过矩阵[λI-Lf,Lfl]去掉第n列得到的矩阵,故rank(λI-Lf,Lfl)≥rank(Hp)=n。且[λI-Lf,Lfl]∈Rn×(n+1),所以rank(λI-Lf,Lfl)=n,由引理1(3)可知系统能控。
3.2 有向路径增加逆向边对系统能控性的影响
假定一个由n+1个节点构成的有向路径,在上述节点编号下,增加逆向边是指增加一条从节点vj指向节点vi的有向边,其中1)跟随者vj指向领导者vi:i=n+1,j=1,…,n或2)跟随者vj指向跟随者vi:i,j=1,…n,且j>i。在有向路径中增加逆向边,相应的Laplacian形式如下:
其中,“*”位置的元素根据拓扑图是否存在相应的逆向边,可能为零可能不为零,即
进一步可以得到定理2。
定理2对于有向符号路径中增加逆向边形成的新拓扑图G,如果选择有向路径中的初始节点为领导者,那么它对应的多智能体系统是单领导者能控的。
证明:1)假定增加的逆向边是从跟随者节点vi,i=1,…,n指向领导者节点,这种情况相当于增加了从跟随者指向领导者的有向边,由命题1可知增加这种连接关系不改变原有系统的能控性,此时系统仍是选择路径初始节点为领导者时系统单领导者能控的。
2)假定增加的逆向边是从节点vj指向节点vi,i,j=1,2,…,n且j>i。跟随者节点的状态按照式(3)更新,此时的能控性与Lf和Lfl有关,利用Lf和Lfl构造矩阵[λI-Lf,Lfl],采用与定理1相似的思路,可以得到该矩阵是满秩的,即rank(λI-Lf,Lfl)=n,所以该系统是选择路径初始节点为领导者时单领导者能控的。
通过上面的分析可以看出在有向路径中增加逆向边形成的新的网络拓扑的能控性等价于未加逆向边时有向路径的能控性。这也给我们在判断一个较为复杂的有向网络拓扑的能控性时,提供了一种新的思路:很多网络拓扑都可以看作是由有向路径增加逆向边而得到的,如图1所示的几类特殊的网络拓扑。

图1 有向路径中增加逆向边形成的几类拓扑图Fig.1 Several classes of topological graphs formed by adding reverse edges to a directed path
图1所示的4个拓扑结构都是通过在有向路径的基础上增加逆向边(图1中的红色边)得到的。以拓扑图1b为例,拓扑图1b是在有向路径9→1→2→…→8的基础上增加一条8→3的逆向边形成的,此时选择有向路径的初始节点9为领导者,给定控制输入信号,对应的多智能体系统是单领导者能控的,这也进一步印证了定理2中的结论。
由以上分析可知,在有向路径中增加逆向边并不会改变系统选择路径初始节点为领导者时系统单领导者能控的性质。
3.3 有向路径增加顺向边对系统能控性的影响
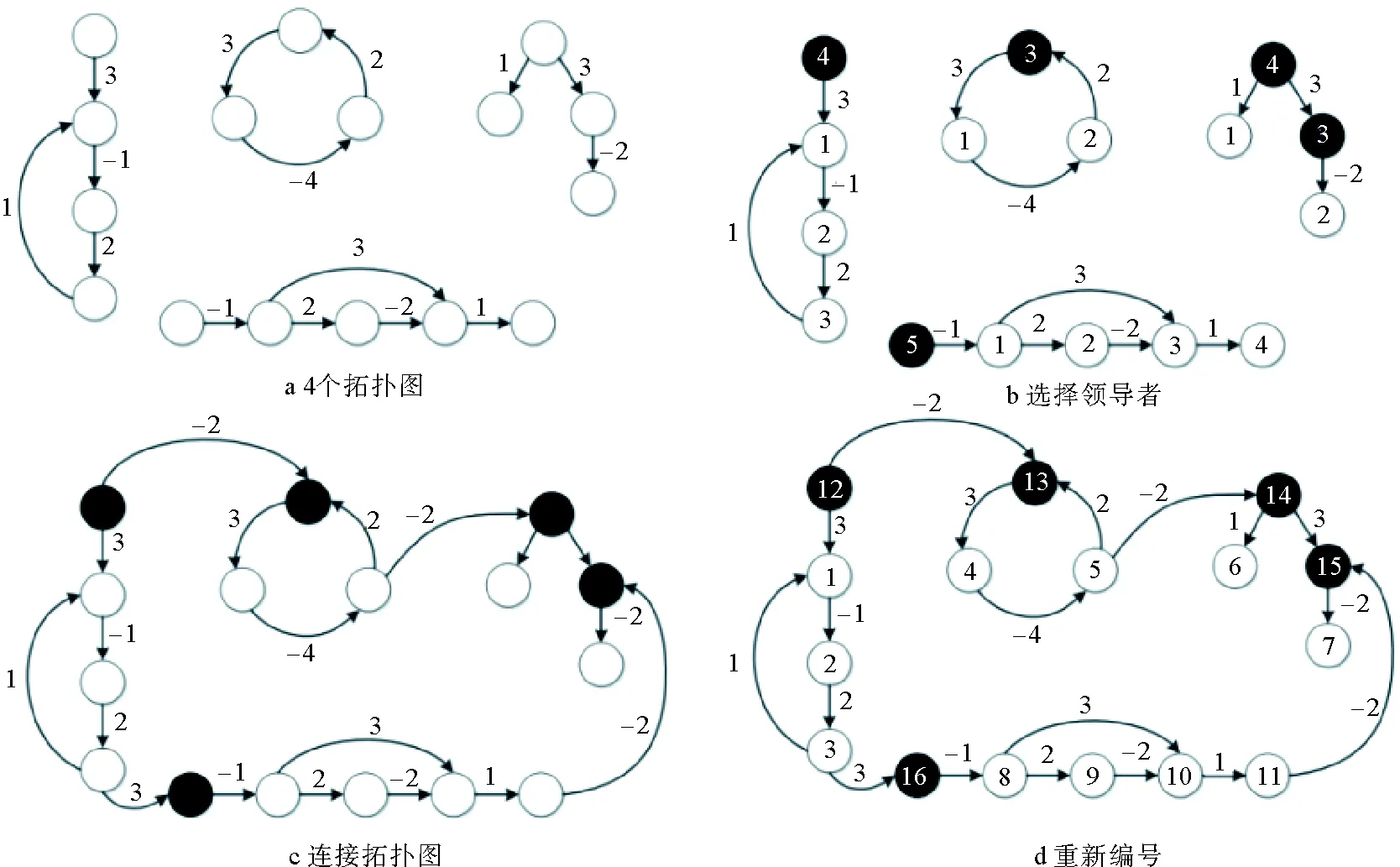
在有向路径中增加顺向边时,选择路径初始节点为领导者的情况下,利用前面的节点编号规则,即在有向路径的基础上,增加一条从节点vi指向节点vj的有向边或者增加一条从节点vn+1指向节点vj的有向边,其中i,j=1,…,n,且i 其中,“*”位置的元素根据拓扑图是否存在相应的顺向边,可能为零也可能不为零。通过Laplacian矩阵的形式可以看出,该矩阵无法利用前面的分析方法得到选择路径初始节点为领导者时对应多智能体系统是单领导者能控的结论。图2为一个由5个节点构成的有向路径拓扑结构,且增加了一条从v2指向v4的顺向边,验证发现此时系统的能控性与权重a32与a42的取值是否相等有关,在其他边权重取值任意的情况下,当a32=a42时系统是不 图2 5节点有向路径增加顺向边拓扑图Fig.2 5-node topology graph formed by adding a forward edge to a directed path 能控的,而当a32≠a42时系统能控。这也可以得出,有向路径增加顺向边形成的拓扑图的能控性是不能直接确定的,根据某些边权重取值的不同,可能导致不同的能控性。有向路径增加顺向边导致系统能控性的不同可以借助图的划分来进行理解,首先给出leader-follower结构下跟随者节点集的几乎等价划分的定义,在此基础上进行分析。 定义4 跟随者节点集的几乎等价划分假定图G=(V,E,A)是一个符号有向图,π=πf∪πl={C1,C2,…,Cr}∪{Cr+1,…,Cn}是图G的一个划分。πf={C1,C2,…,Cr}是对应跟随者节点的一个几乎等价划分,对任意的vs,vt∈Ci,i=1,…,r,j=1,…,r,r+1,…,n,i≠j,下列等式成立: 其中,ask和atk分别表示节点vk∈Cj指向vs∈Ci的有向边权重以及vk∈Cj指向vt∈Ci的有向边权重。 定义5 基于单领导者的跟随者节点集的非平凡划分假定π=πf∪πl={C1,C2,…,Cr}∪{Cr+1}是图G的一个划分,πf={C1,C2,…,Cr}是跟随者集的非平凡几乎等价划分,且Cr+1中仅包含一个领导者节点,那么称此时的划分πf为基于单领导者的跟随者节点集的非平凡划分。 定义6 跟随者特征矩阵跟随者节点集Vf={v1,v2,…,vn}的一个划分πf={C1,C2,…,Cr}的特征矩阵Pf∈Rn×r是由跟随者节点形成的每个胞腔的特征向量作为其列向量形成的矩阵。矩阵Pf中的元素定义为 引理3[26]对于矩阵M∈Rn×n和P∈Rn×r,im(P)是M的不变子空间的充要条件是存在一个矩阵Q∈Rr×r满足MP=PQ。 引理4[27]给定矩阵A∈Rn×n和B∈Rn×r,用〈A,B〉表示包含im(B)的最小A-不变子空间。矩阵对(A,B)是能控的条件是dim(〈A,B〉)=n。 定理3对于有向路径增加顺向边形成的新拓扑图G,如果跟随者节点中存在非平凡胞腔,那么该拓扑结构对应的多智能体系统是选择初始节点为领导者不能控的。 证明:因为πf={C1,C2,…,Cr}是图G中跟随者节点集Vf={v1,v2,…,vn}的一个几乎等价划分,且Pf是划分πf的特征矩阵,根据引理3和引理4,im(Pf)是Lf的不变子空间。由于跟随者节点中存在非平凡胞腔,r 由定理3可以得到若跟随者节点中存在非平凡胞腔,则对应的多智能体系统是不能控的。而如图2所示,增加顺向边会增加出现非平凡胞腔的可能性。 在这一部分中,首先考虑将多个能控有向符号路径图通过特定连接关系进行连接,形成一个能控的有向树图,进而得到有向树图能控时的领导者选择方式。然后将多个有向符号路径图加边形成的能控拓扑图通过特定连接关系进行连接,形成一类更广泛的能控复杂有向符号拓扑图,进而得到该拓扑图能控时的领导者选择方式。 在多个有向符号路径间增加特殊节点之间的连接关系,便可以得到有向树图。需要特别说明的是,之前的许多文献关于有向树图的能控性描述都是基于选择根节点为领导者,系统单领导者能控的充要条件是不同分支上的边权重不同。本文的研究工作将不再规定不同分支边权重不同和选择单领导者使得系统能控这两个条件,而是通过在有向树图中选择多个领导者,得到在任意边权重的情况下有向树图能控的条件。通过命题2和定理1可以直接得到关于有向符号树图的推论1。 例1给定一个如图3a所示的有向符号树图G表示的多智能体系统,该符号有向树图划分为5个有向符号路径子图Gi,i=1,…,5,其中V1={v1,v2,v3,v4},V2={v5,v6,v7,v8},V3={v9,v10,v11},V4={v12,v13},V5={v14,v15}。如图3b所示,选定的领导者集为Vl={v1,v5,v9,v12,v14},在该领导者位置的选取方式下,根据定理1和命题2,该有向符号树图表示的多智能体系统是能控的。 图3 14个节点构成的有向树图Fig.3 A directed tree graph composed of 14 nodes 除了上述多个有向符号路径可以形成有向符号树图之外,我们知道许多有向拓扑图都可以看作是在有向路径图或者有向路径加边形成的拓扑图中增加不同拓扑图之间的连接关系而形成的。具体来说,前面的分析得到了有向路径以及有向路径加边形成的拓扑能控的条件,我们将单个有向路径或者单个有向路径加边形成的拓扑看做是一个个子图,利用前面得到的定理1~3给定使得每个子图能控的领导者位置的选取方式,结合命题2,在不同子图间通过领导者之间以及跟随者指向领导者的有向边连接形成的新的拓扑结构仍是能控的结论,可以得到一类更广泛的能控有向符号拓扑。 图4 能控复杂有向符号拓扑的构造过程Fig.4 The construction process of controllable complex directed signed topology 本文研究的是基于leader-follower结构有向符号多智能体系统的能控性问题。针对leader-follower结构特点,提出了有向拓扑下改变领导者和领导者之间以及跟随者指向领导者的有向边,不改变系统能控性的性质(命题1、2),以有向路径以及有向路径加边形成的新拓扑为基础,给出了有向路径以及加逆向边和顺向边时系统能控的条件。具体来说,首先对有向路径进行了研究,得到选择有向路径中的初始节点为领导者时系统是单领导者能控的(定理1)。进一步,在有向路径的基础上增加逆向边并不改变系统原来的能控性(定理2),但增加顺向边时能控性的情况比较复杂,能控性可能改变,也可能不改变,这取决于选定初始节点为领导者时,跟随者节点中是否存在非平凡胞腔(定理3)。最后,在前面的基础上,给出了一类更广泛的能控复杂有向符号拓扑的构造方法,可以利用简单能控拓扑图通过特殊节点间的连接关系快速得到一类比较复杂的能控拓扑图。文中利用具体的例子进行了相关的解释和说明。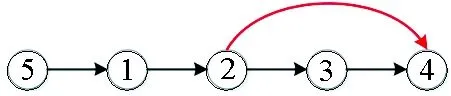

4 能控复杂有向符号拓扑的构造
4.1 有向符号树图


4.2 一类更广泛的能控有向符号拓扑的构造

5 总结
