Evolution Toward the Observational Features of a Stripped Envelope Type IIb Supernova in a Binary System
2022-05-24GangLongHanFengSongRuiYuZhangYingQinLiuYanZhaoShiTaoQiandFangWenWu
Gang Long ,Han-Feng Song ,Rui-Yu Zhang ,Ying Qin ,Liu-Yan Zhao ,Shi-Tao Qi ,and Fang-Wen Wu
1 College of Physics,Guizhou University,Guiyang 550025,China;songhanfeng@163.com
2 College of Physics,Henan Normal University,Xinxiang 453007,China
3 Department of Physics,Anhui Normal University,Wuhu 241000,China
Abstract Type IIb supernovae(SNe IIb)that have a thin layer of hydrogen left in their outer envelope have been believed to belong to core collapse supernovae.Mass transfer via Roche lobe overflow can significantly change the nucleosynthesis and surface chemical elements of the progenitors of SNe IIb.We aim to explore what conditions a close binary can meet with the observational features of SNe IIb.We find that an observed low mass SN IIb cannot be produced by a low mass isolated star with M <20 M⊙due to the existence of a thick hydrogen envelope regardless of rotation.Binaries dominate as progenitors in the mass interval (i.e.,M <20 M⊙) considered in this paper.The 16 M⊙primary with a 14 M⊙companion in a binary system with~10 days <Porb <720 days can reproduce observational features of SNe IIb (i.e.,Teff, With the decrease of the hydrogen-rich envelope mass,the radius of the progenitor shrinks.The associated types of SN IIb progenitors from RSGs and YSGs to BSGs are closely related to the amount of hydrogen left in the envelopes.Rotation can bring the production of the CNO reaction to the stellar surface at an early phase,which would explain the nitrogen-rich circumstellar material of SN 1993J and can also explain the large He/H ratio of supernova ejecta.Rotation can increase the corresponding region of the orbital period which can produce an SN IIb.
Key words:(stars:) binaries (including multiple):close– stars:evolution– stars:rotation– stars:abundances
1.Introduction
A type IIb supernova (SN IIb) has initially faint hydrogen emission in its spectrum.However,at the subsequent stage,the hydrogen line cannot be detected by observers.There is also a second peak in the light curve,whose spectrum is closer to a type Ib supernova.This fact indicates that as the ejecta expands,the hydrogen layer rapidly becomes more transparent and displays the deeper layer.The physical mechanisms that drive the stripping of the hydrogen envelope and the parameter regimes in which they dominate the formation of SNe IIb are still open questions.There are four evolutionary channels which can reproduce a progenitor of an SN IIb.They are the single star evolution,Roche lobe overflow (RLOF) scenario(Gilkis et al.2019;Sravan et al.2019),binary evolution channel with grazing envelope evolution (GEE,Torrey et al.2019) and fatal common envelope evolution (CEE,where the secondary star merges with the core of the giant primary star)(Soker 2017;Lohev et al.2019).The progenitor of an SN IIb might be a more massive star (≥~30 M⊙) that stripped the hydrogen envelope via strong stellar winds.By studying the evolution of massive single stars,Georgy et al.(2012)found a suitable progenitor born with 20 M⊙and ending with the correct core mass,hydrogen content,luminosity and color to explain the complete set of observations of SN 2008ax.Groh et al.(2013) reinterpreted the final stage of the rotating model as a luminous blue variable (LBV) star and suggested that LBVs may be the progenitors of some core collapse supernovae (SNe).However,the observed stripping envelope SN rates are too high to be explained solely by single star evolution.Moreover,wind clumping in stellar winds implies that the lower wind loss rate is not conducive to the production of an SN IIb.
Most of the hydrogen-rich envelope is lost by the interaction with the companions in a binary system,leaving a core composed almost entirely of helium (2 M⊙<MHe<6 M⊙)(RLOF scenario).The stellar evolution of the isolated star requires a very precise adjustment of the initial parameters in order to leave a thin hydrogen envelope before the explosion.The binary evolutionary channel of an SN IIb can be strengthened by two main reasons.First,mass loss can be much more naturally interpreted by the RLOF.Second,the foundation of the companion star in SN 1993J and SN 2001ig can highlight the binary channel.The fatal CEE scenario can also account for some SNe IIb.A low mass main sequence secondary star inspirals inside the giant envelope of the massive primary star and removes most of the giant envelope before it merges with the giant core.However,it has several uncertainties in the calculations,such as the outcome of the CEE,the merger process and wind mass-loss rate.In this scenario,there are some physical processes involving the ejection of a common envelope (Podsiadlowski et al.1992;Yoon et al.2010,2017),thermal nuclear reaction instabilities(Arnett &Meakin 2011;Strotjohann et al.2015),stellar evolution with rotation (Groh et al.2013;Soker 2017) and mass removal via strong winds (Woosley et al.1994;Heger et al.2003;Georgy et al.2012;Groh et al.2013;Soker 2017).Torrey et al.(2019) introduced an enhanced mass loss due to jets that the secondary star might launch,and find that the enhanced mass loss brings the binary system to experience GEE and form a progenitor of an SN IIb.The GEE is an additional mass transfer scenario,different from the RLOF scenario,and hence expands the binary parameter space that can lead to SNe IIb.At present,it is an important task to construct a detailed model which can explain the observational features of the stripped envelope SNe IIb.
Axis rotation is a very important physical process which needs to be fully considered in the evolution of massive stars(Langer 2012;Maeder &Meynet 2012).Rapid rotation can trigger strong stellar winds and it can eliminate a large amount of material from the stellar surface.The faster the rotational speed is,the larger the stellar wind.Note that rapid rotation can drive various instabilities in the star.In particular,meridional circulations and shear turbulence can transfer angular momentum and mix chemical species in the star (Song et al.2013,2016).The mixing of chemical elements might be the most important effect of rotation in massive stars (Zahn 1992;Mathis &Zahn 2004).Thus,fresh nitrogen and helium can appear on the stellar surface and constantly become more abundant over time during the main sequence (Maeder &Meynet 2000,2012).
An interacting binary can change the structure of SN progenitors dramatically.A famous example is SN 1987A.Its surrounding ring can be ascribed to the binary interaction(Podsiadlowski &Joss 1989).SN 1993J and SN 2011dh are SNe IIb and they have experienced significant mass loss (Van Dyk et al.2011).These models often require matter to flow from the primary to the companion at different stages of its evolution.The channel of the binary system can give rise to the low mass of an SN IIb progenitor and the survival of a massive companion near the SN remnant.In contrast to the isolated counterparts,these characteristics can fit with the observations of the SN IIb SN 1993J.
In this paper,we intend to explore what conditions can succeed in producing SNe IIb in the close binary evolution scenario.We aim to explore the following questions in the binary scenario:(1) how rotation has an important impact on the formation of SNe IIb,(2) how surface nitrogen abundance of the progenitor star evolves with evolutionary age,(3) what controls the residual hydrogen under the influence of mass transfer due to RLOF,(4) what is the relationship between SN IIb with other types of SNe,such as SNe IIP,IIL and Ib/c,(5)how the internal structure of the deep core may be influenced by rotation and RLOF and(6)how different theoretical models can explain the surface parameters of SNe IIb,such as the masses of hydrogen envelopes and helium cores,the preexplosion images,the stellar radii and mass loss rates.
2.The Initial Model Parameters Used in the Calculations
We rely on the MESA code to investigate the evolution of the progenitors of SNe IIb (Paxton et al.2011,2013,2015,2018).We adopt the Schwarzschild criterion to dominate the size of the convective zone.The mixing length can be given by lm=1.5HP,where HPdenotes the pressure scale height.An overshooting parameter of 0.12 pressure scale heights is considered as the standard value.We set the initial chemical composition to be the solar one (i.e.,X=0.7,Y=0.28,Z=0.02) (Peimbert et al.2007;Brott et al.2011).We have included the basic.net,coburn.net and approx21.net nuclear networks in MESA.Our initial models are composed of one or two zero age main sequence(ZAMS)components with various parameters which are listed in Table 1.The efficiency of mass transfer via RLOF is then given by βmt=0.5.Half of the transferred mass via RLOF is directly ejected out from the system.The Dutch scheme for both hot and cool wind mass loss rates has been adopted and the Dutch scaling factor is 1.0.The Wolf-Rayet (WR) wind mass-loss rates are calculated according to Nugis &Lamers (2000).The opacities are computed from the OPAL tables (Iglesias &Rogers 1996).
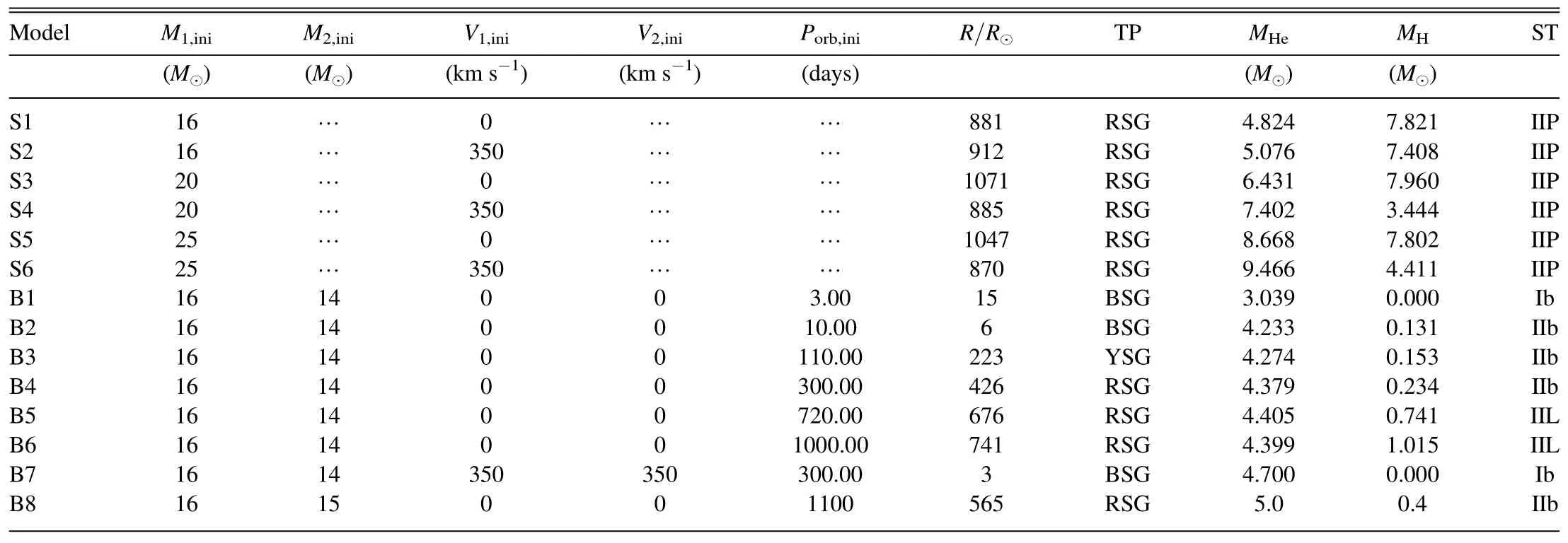
Table 1 The Initial Model Parameters Used in the Calculations
We include various rotationally induced instabilities that lead to the mixing of chemical elements,such as the meridional circulation,secular and dynamical shear instabilities,and the Goldreich–Schubert–Fricke instability.The rotational mixing due to these hydrodynamical instabilities has been considered as a diffusive process according to Heger et al.(2000);Peng et al.(2022).The diffusion coefficients are included in the diffusion equation and they are adopted for the transportation of both the angular momentum and chemical elements.The rotationally induced instabilities are decreased by a factor fc=0.0228.This parameter has been updated to satisfy the observed nitrogen abundances versus the projected rotational velocities for the samples from the Large Magellanic Cloud(Arnett &Meakin 2011).The gradient of the mean molecular weight gradients significantly suppresses the rotational mixing.In order to meet with the observations,the efficiency of rotational mixing can be regulated by the factor fμ.We make use of a value fμ=0.1 as in Yoon et al.(2006) who corrected this factor to be consistent with the observed surface helium.
We treat the model to be an SN IIP or SN IIL when the final hydrogen envelope mass is greater than 0.5 M⊙.Actually,together with extinction and distance uncertainties in progenitor data,it is very difficult to derive an accurate hydrogen envelope mass from the pre-explosion imaging.The amount of hydrogen left in the envelope at the time of explosion is closelyrelated to the mass-loss rate and it also likely involves binary interaction.The weakening of hydrogen lines in an SN IIb implies that the SN IIb progenitor has a tiny hydrogen envelope mass at the time of explosion,MH≈0.03–0.5 M⊙(Woosley et al.1994;Meynet et al.2015;Yoon et al.2017),with a possible smaller mass limit of even down to MH≈0.01 M⊙(Dessart et al.2011;Eldridge et al.2018).Sravan et al.(2018)set the hydrogen envelope of the SN IIb progenitor at the onset of explosion to have a mass of 0.01 M⊙<MH<1.0 M⊙in their population synthesis investigation.Recently,Gilkis &Arcavi(2022) quantify this uncertainty and discovered that available data are consistent with a proposed type Ib-IIb hydrogen mass threshold of MH≈0.033 M⊙,implying that even SN Ib progenitors are not pure helium stars.When the hydrogen envelope mass is less than 0.033 M⊙,the star explodes as an SN Ib or Ic.Models with hydrogen envelope mass between 0.033 M⊙and 0.5 M⊙are considered as SN IIb progenitors in this paper.
The final evolutionary outcomes for an isolated star and the primary in a binary system are also summarized in Table 1.The binary orbit is circular and the Roche lobe radius is taken from Eggleton(1983).We chose several initial orbital periods as the different type of mass transfer via RLOF.Case A mass transfer occurs during the main sequence phase(Porb=3.0 days)while Case B mass transfer happens after core H-exhaustion but before the He-ignition in the core (Porb=10.0 days).Case C mass transfer starts during the core He-burning (Porb>~20.0 days).The progenitors are classified into different types according to their effective temperature and surface hydrogen mass fraction as follows:red supergiant (RSG):Teff<4.8 kK,0.01 ≤Xs;yellow supergiant (YSG):4.8 kK <Teff<7.5 kK,0.01 ≤Xs;blue supergiant (BSG):7.5 kK <Teff<55 kK,0.01 ≤Xs.

Table 2 The Observations of SN 1993J and the Theoretical Values in Models B4 and B8
3.Results of Numerical Calculations
3.1.The Evolutionary Tracks in the Hertzsprung-Russell Diagram
Figure 1(a)illustrates the Hertzsprung–Russell(HR)diagram for all models,grouped by mass and rotation in single stars.At the beginning of evolution,the relation between temperature and stellar mass is Teff∝M0.5–0.6,therefore,the higher the stellar mass,the higher the effective temperature.The effective gravity can be significantly decreased by centrifugal force which can be affected by the internal transportation of spin angular momentum from the interior to the surface.Therefore,a star under the influence of rotation displays the surface luminosity characteristics of a lower-mass non-rotating one.The star,therefore,shifts toward lower luminosity and effective temperature when the initial rotational velocity increases.This is also because rapid rotation increases the stellar volume and the mean radius of a star,which results in a lower effective temperature than the non-rotating counterpart.This effect is considered as the dynamical effect of rotation.

Figure 1.(a)Evolutionary tracks of the isolated stars with initial masses of 16 M⊙,20 M⊙and 25 M⊙in the HR diagram.(b)Evolutionary tracks of the primary with initial mass of 16 M⊙in the binary system with initial orbital periods ranging from 3 to 1000 days.(c) The mass of the hydrogen envelope varies with the effective temperature for all isolated stars.(d)The mass of the hydrogen envelope varies with the effective temperature for the 16 M⊙primary in all computed binary models.
The rotationally driven mixing can also increase the hydrogen convective core,causing the evolutionary track to be more luminous and redder.Moreover,the opacity in the hydrogen envelope can be reduced by the increase of helium in the subsequent evolution.This process can cause the star to be more compact and have higher effective temperature.The tracks shift upward and to the left before bending to the right in the HR diagram when the initial rotational velocity becomes higher(Maeder&Meynet 2000,2012;Chieffi&Limongi 2013).After that,the star evolves toward lower effective temperature.This is a consequence of the increase in mean molecular weight.The post main sequence luminosity of the rapidly rotating star is larger,by about a factor of~2.2,than that of a non-rotating counterpart.The reason is that rotational mixing leads to a more massive helium core.This fact indicates that rotating models will be faced with a violent collapse that heats the central core up to a higher density and temperature.
By core contraction after core helium exhaustion,nonrotating single stars spend their last evolutionary phases as RSGs.Enhanced mass loss by rotation implies that tracks for the stars do not attain as far to the right position on the HR diagram as they do for non-rotating stars.The larger helium core in rotating stars can result in faster redward transition from BSGs to RSGs,and,hence,a larger mass loss rate can be induced by the increased luminosity.Therefore,the model S6 slightly shifts toward higher effective temperature after the RSG star.
Comparing our models of single stars with the counterparts in Georgy et al.(2012),the evolutionary track on the HR diagram is similar,but not identical,to that of stars that start on the ZAMS with a mass range of 15–20 M⊙.For example,Georgy et al.(2012) stated that the track of a rotating 20 M⊙model has an H-content in the ejecta of 0.02 M⊙,and a CO-core mass of 4.73 M⊙.The corresponding hydrogen envelope mass at explosion is much less than our model S4.The main difference might be ascribed to the treatments of convective overshooting and initial rotational velocities.The model of Georgy et al.(2012) removes most of the envelope,and the star becomes somewhat bluer than our model S4 that suffers no rapid mass loss.
We display in Figure 1(b) the evolutionary tracks of the primary star with an initial mass of 16 M⊙in the binary system with the initial orbital periods ranging from 3 to 1000 days.Since the orbital period in model B1 with Porb=3.0 days is so short,the primary star can go through the first event of RLOF during core hydrogen burning.The primary stays in the semidetached state up to the core hydrogen exhaustion.The primary star transfers mass to the companion star so its luminosity falls down rapidly.The primary star deviates from thermal equilibrium.When the rate of mass transfer via RLOF become lower,the stars have enough time to adjust and attain both hydrostatic and thermal equilibrium again.Because of the expansion of the envelope,the primary star experiences the second episode of RLOF until the core helium burning.In the subsequent evolution,the strong stellar wind decreases the hydrogen envelope mass gradually,and the star shifts toward a higher effective temperature in the HR diagram.The shell of hydrogen burning can be extinguished and removed readily.Then,most of the core helium is depleted during the blue excursion.When the core helium is burned out,the burning of helium in the shell can cause the star to expand again.At the same time,the deep layers can experience advanced nuclear reactions before the final collapse.The stellar mass is only 3.04 M⊙when it explodes.The star has lost the whole hydrogen envelope.Therefore,the primary finally appears as a BSG and explode as an SN Ib.It is worth noting that this star is not an SN Ic because the progenitor has a 1.47 M⊙helium envelope.An SN Ic has a small helium envelope mass(MHe<0.1 M⊙).The current orbital period of the system is about 51.6 days and two components are clearly separated because of mass transfer.
In this system,the secondary has obtained a part of the transferred mass,being of 18.87 M⊙.The companion star still burns hydrogen at its core.Because there is a large amount of matter which can transfer from the primary,the central core of the secondary can be enlarged by the structural readjustment.The reason is that the central temperature and the convection core become larger when the central pressure is increased by mass accretion.Fresh hydrogen above the previous core can be mixed by convection and the central hydrogen abundance can be increased accordingly.The star is rejuvenated and then behaves like a younger star.The star does not shift further from the position of the ZAMS.It has not filled its Roche lobe.Another important feature of the companion star is that its internal structure is significantly different from a single star with the same mass,which has not experienced the accretion.The companion star is appreciably over-luminous because of mass accretion when the primary explodes.One of the observational counterparts of an SN Ib progenitor is HD 45166.This system is composed of an enriched helium 4.2 M⊙primary star with R ≈1.0 R⊙and a companion star which evolves on the main sequence.The system has an orbital period of 1.596 days (Boian &Groh 2018).However,the observed low-mass (M=3–5 M⊙) helium star can display a higher effective temperature,but it becomes visually very faint because of a lower luminosity with the evolution of core helium burning.However,the star becomes cooler and more luminous at the final evolutionary stage because there exists a rapidly expanding envelope.
Let us consider the same initial mass 16 M⊙as in the binary system B2 but with an initial orbital period of 10 days.The system goes through the first event of RLOF after the main sequence.The primary can transport most of its mass to the companion at the beginning of the core helium burning(Case B mass transfer).More hydrogen can be retained after RLOF in model B2 in contrast to model B1.The reason is that the stripping process becomes less efficient in an initially wider system.After the mass transfer process,the stripped primary shrinks and attempts to reach a new thermal equilibrium.At the same time,the helium burning has already ignited in the convective core.From the minimum value of the luminosity,the main mechanism of structural adjustment is the carbon burning.The primary star in the initially tighter system B1 becomes hotter and more compact than the one in model B2 because the model B1 has a slight hydrogen envelope.Thus this process can reduce significantly the radius of the primary.Model B1 has a mass of 3.12 M⊙at core helium exhaustion.After that,the star loses all of its remaining hydrogen envelope because of strong stellar winds.Model B2 has a mass of 4.39 M⊙and a hydrogen envelope mass of 0.17 M⊙.Then,it also can form a large blueward excursion because there is helium burning in the core.The evolutionary track of the star returns to the low effective temperature.Then,the star experiences the advanced central nuclear burning and finally blows up as a supernova.The progenitor of the SN has an outermost hydrogen envelope of 0.13 M⊙and the total mass of this star is 4.36 M⊙.This is a YSG progenitor that explodes as an SN IIb.For the system B2,the rate of mass transfer is larger than the one in the system B1.This is because the thermal timescale of the star becomes much shorter at the moment that the RLOF begins.Therefore,the final orbital period of the system is about 89 days.
The system B6 with a longer initial orbital period of 1000 days can give rise to Case C mass transfer.The RLOF occurs at a central helium fraction of 0.974.The occurrence of Case C mass transfer is closely related to the evolution of stellar radius.One can find that the peak value of mass transfer rate via RLOF can reach 6.6×10-3M⊙yr-1.Carbon can be ignited at the subsequent stage and results in a higher luminosity.When the explosion occurs,the progenitor has a mass of 5.414 M⊙whereas its companion grows to 18.139 M⊙.This model can account for the luminosity of an SN IIL progenitor in the HR diagram.Furthermore,one also notices that both extended blue loops and blueward excursions can be increased by rotation in the binary system B7.
3.2.Comparison with the Other Binary Works
Our theoretical results differ from the other work on modeling the progenitor of SN 1993J.Claeys et al.(2011)also found channels to SNe IIb via Case A and early Case B mass transfer.The difference between the two results is slightly large due to the adopted wind mass-loss prescription.Claeys et al.(2011) adopted the prescription of de Jager et al.(1988)during the entire stellar evolution,which is about two orders of magnitude lower than our WR mass-loss prescription of Nugis&Lamers (2000) and drives most of the stripping in our case.More recently,Yoon et al.(2017)extended the analysis for SN IIb progenitors to low metallicity.They found a significant difference in the availability of early Case B mass transfer channels toward SNe IIb between solar and low metallicities.The star with lower metallicity is prone to generate the blue supergiant SN IIb progenitors with a more compact structure and it can contain a very tiny hydrogen envelope mass at the time of SN explosion.Sravan et al.(2019) investigated theeffect of mass ratio and mass transfer efficiency on binary SN IIb channels at both solar and low metallicities.They found that the viability of the evolutionary channels mentioned above increases with increasing initial mass ratio and decreasing mass transfer efficiency.
So far,five SN IIb progenitor candidates have been identified in pre-explosion images:SNe 1993J,2008ax,2011dh,2013df and 2016gkg.They are the important fundamental factors for constraining the evolution of SN IIb progenitors.In order to compare the theoretical results with observations,we have marked the positions of five SNe IIb in the HR diagram.There are also some evidences for binary companions of the progenitors of SN 1993J,SN 2001ig and SN 2011dh.At present,only the effective temperature and luminosity of the companion star of SN 1993J have been identified.They are listed in Table 2.The observational position of two component stars in the HR diagram can provide us with a good tool to constrain the theoretical model and the evolutionary characteristics.The evolution of two components in the HR diagram can be traced by the model B4.At the time of SN explosion,the primary star fits well with the the pre-explosion observationsHowever,the secondary star in model B4 is approximately consistent with observations.The secondary has the right luminosity to match the observations,but it is too blue.The star is shifted to a higher effective temperature by just(see Table 2).Stancliffe &Eldridge (2009)demonstrated that it is extremely difficult to obtain the secondary in the right place in the HR diagram.The observational position indicates that the secondary is extremely close to (or just beyond) the end of its main sequence.They find that this can only be done in a very narrow range of initial masses and periods.The position of the companion star also heavily depends on the value of accretion efficiency β(Benvenuto et al.2013).The effective temperature and luminosity of the companion star of SN 1993J decrease for lower accretion efficiencies.Stancliffe &Eldridge (2009)noticed that if mass transfer is conservative,the observations can be reproduced by a system consisting of a 15 M⊙primary and a 14 M⊙secondary in an orbit with an initial period of 2100 days.However,they used a high metallicity model with Z=0.04.We simulate the system SN 1993J composed of a 16 M⊙primary and a 15 M⊙secondary in an orbit with an initial period of 1100 days.The metallicity is Z=0.04 and the accretion efficiency is set to be β=0.15.The final positions for two components in the HR diagram agree well with observations (see Table 2 and Figure 2).
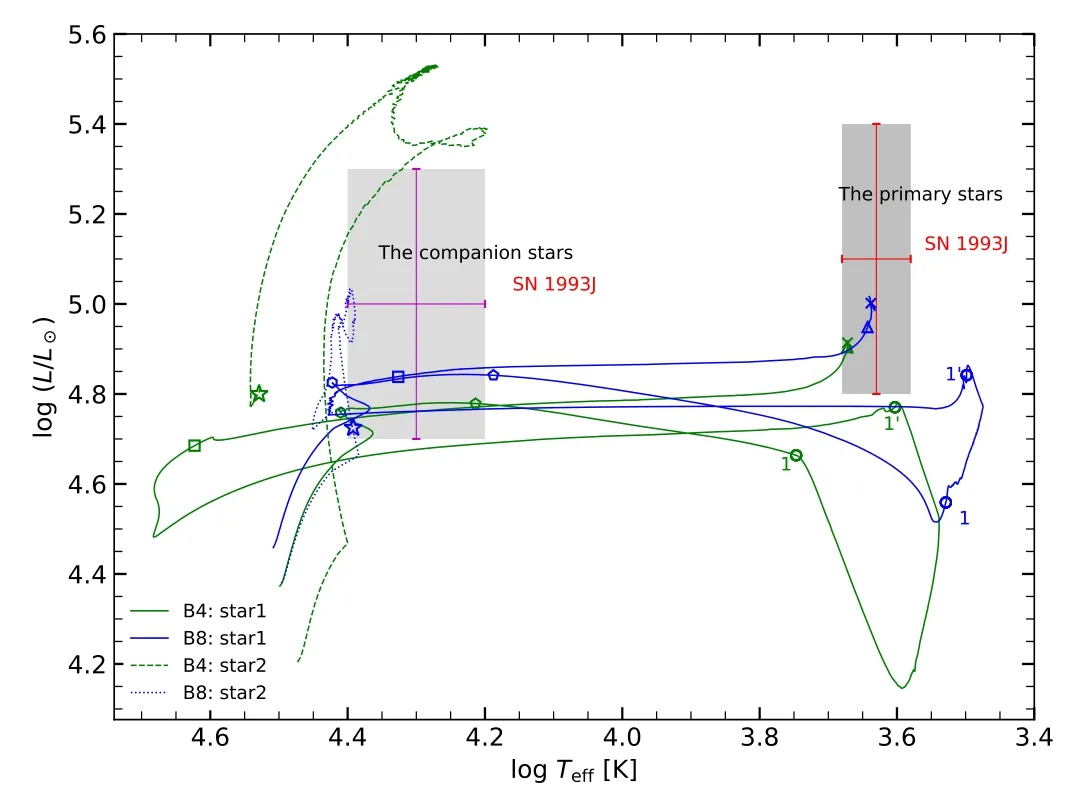
Figure 2.Evolutionary tracks of two component stars with the initial mass of 16 M⊙in the binary systems B4 and B8.
Figure 3.(a)The surface helium mass fraction varies with the effective temperature for all single stars.(b)The surface helium mass fraction varies with the effective temperature for the 16 M⊙primary star in all binary models.(c)The surface mass fraction ratio of nitrogen to carbon varies with the effective temperature for all single stars.(d) The surface mass fraction ratio of nitrogen to carbon varies with the effective temperature for the 16 M⊙primary star in all binary models.
3.3.The Variation of Hydrogen Envelope Mass
Figures 1(c)and(d)illustrate how the mass of the hydrogen envelope varies with effective temperature in an isolated star and the primary in binaries.The hydrogen envelope mass is an important criterion for distinguishing from various types of SNe.In the single star scenario,all models finally explode as RSGs because of the existence of a thick hydrogen envelope(see Figure 1(a)).This fact indicates that stellar winds are too weak to remove the hydrogen envelope.Actually,an evolution to blue after the RSG star occurs when the core mass fraction is greater than a lower limit value by about 70% of the stellar mass.This implies that the yellow or BSG will have a hydrogen envelope that is less than about 30% of the total mass.In the binary scenario,the physical mechanisms of the mass loss via RLOF are governed by the orbital separation and stellar radius.The rate of mass transfer via RLOF heavily depends on the radius excess (i.e.,the difference between stellar radius and radius of the Roche lobe).The mass transfer terminates when the radius of the primary is smaller than its Roche lobe.Interestingly,depending on the two different physical mechanisms for mass removal,the stellar structure is quite different at the pre-SN stage.Our results affirm that mass transfer via RLOF can give rise to a much thinner hydrogen envelope than stellar winds.The smaller the orbital period is,the less thick the hydrogen envelope becomes.There is a decreasing trend of the hydrogen envelope mass in the sequence from SNe IIP and IIL to IIb.The SN IIb progenitor has a tiny hydrogen envelope mass at the time of explosion,MH⋍0.033–0.5 M⊙.When the hydrogen envelope mass is lower than this mass threshold or range,the progenitor would be a WN star.After the WN stage,the star would explode as an SN Ib.The leftover hydrogen envelope mass in the envelope has an important impact on progenitor properties,such as temperature and photospheric radius,in non-trivial ways.In fact,a peak in progenitor envelope mass translates to a peak in radius,and vice versa.The extended model produces a pronounced spike at the early stage (at the time 5 days after the SN explosion) of the observed bolometric light curves of the SN IIb while the compact progenitor displays a much weaker bump.The difference is mostly due to the extra amount of energy required to expand a more compact structure.Moreover,the more extended the progenitor structure is,the higher the luminosity and temperature of the emitting region right after shock breakout,and the slower the subsequent decline (Bersten et al.2012).
We find that for MH>~0.1 M⊙,with the decrease of the leftover hydrogen envelope,the stellar radius becomes smaller while the effective temperature becomes larger.This difference might be a way to distinguish between the isolated and binary channels for producing yellow or red progenitors of SNe (see Table 1).However,for MH<~0.1 M⊙,the evolution of the radius has no relevance to the mass of the hydrogen envelope but is closely related to the expansion of the helium envelope.Thus,the relationship between SNe IIb and other types of SNe,such as SNe IIP,IIL and Ib/c,strongly depends on the hydrogen envelope leftover.
3.4.The Evolution of the Surface Chemical Elements
Figures 3(a) and (b) illustrate that the chemical enrichments vary with the evolutionary age in isolated stars and the primary in binaries with various initial orbital periods.In non-rotating stars S1,S3 and S5,chemical mixing occurs only in the core due to convection and convective overshooting.However,these stars do not develop a convective envelope during the core hydrogen burning.Therefore,there are no other physical mechanisms which can bring nuclear material to the surface.Figures 4(a) and (b) display the evolution of the hydrogen abundance for single stars and the binary system with various orbital periods.One can find that the surface hydrogen abundance in non-rotating single stars drops slightly at the core hydrogen exhaustion.This indicates that the convective dredge-up can increase helium and other heavy elements (i.e.,14N)from the deep layers to the surface.We find in Figure 4(a)that during the post-main sequence,surface hydrogen in model S1 drops from 0.7 to 0.65 while it falls down from 0.65 to 0.45 in model S5.This implies that convective dredge-up is more efficient in the more massive star than in the less massive counterpart.

Figure 4.(a) The surface hydrogen mass fraction varies with the evolutionary age for all isolated stars.(b) The surface hydrogen abundance varies with the evolutionary age for the 16 M⊙primary in all binary models.(c) The mass of helium cores varies with the evolutionary age for single stars.(d)The mass of helium cores varies with the evolutionary time for the 16 M⊙primary in all binary models.
Rapid rotation in a star can give rise to meridional circulation and shear turbulence,which can mix nuclear products from the convective core all the way up to the surface in models S2,S4 and S6.The first element to illustrate an enriched abundance is nitrogen,produced by the CNO cycle while carbon is depleted during the main sequence.Rotation-induced mixing can also bring central helium to the surface while hydrogen in the envelope can be transferred to the core (see Figure 4(a)).One can find that helium and the ratio of nitrogen to carbon N/C goes up while surface hydrogen reduces with the increase of stellar mass and initial rotation velocity(Song et al.2018).This can also result in a higher He/H ratio.However,the helium enrichment on the surface is much slower than the nitrogen abundance,as the inner helium gradient is much smaller than the nitrogen gradient(see panels(a)and(c)).A steeper nitrogen gradient is beneficial to give rise to nitrogen diffusion.The ratio of N/C goes up with the evolutionary age because more new nuclear reaction products can reach the surface.Therefore,rotation brings CNO products to the surface at an early time in contrast to the non-rotating counterpart.Rotational mixing is the strongest at the main sequence phase because the rotational velocity can maintain a higher value.At the post main sequence stage,the star can be spun down by stellar expansion,or it loses spin angular momentum significantly via strong stellar winds.Although rotational mixing can be decreased slightly,nitrogen enrichment is obvious because of the combined effect of the convective dredge-up and the enhanced wind.The convection region can extend to the upper region above the hydrogen burning shell.
The strong RSG wind can also expose the enriched nitrogen layer.Much of the difference in the chemical structure of the rotating pre-SN and non-rotating one arises during the evolution of the main sequence evolution.The lifetime of the advanced stage is too short to allow significant effects for most rotational instabilities.Including rapid rotation in the progenitor model has many advantages.It can explain the N-rich circumstellar material.For example,the ultraviolet line of SN 1993J is wide with a box shape,originating from the ejections and a cold and dense shell.The shape of the line is well fitted by a fast moving shell with inner velocity~7000 km s-1.A strong signal of nitrogen enrichment is noticed in the shell,with the ratio of N/C ≈12.4 in the SN IIb SN 1993J.The ejecta of SN 1987A,with a velocity of ≥30,000 km s-1,has an unexpectedly large He/H ratio of 0.2 by number,i.e.,Y=0.4.The high ratio of nitrogen to carbon in the ejecta of SN 1993J can be easily explained because the rotational mixing can bring central nitrogen to the surface and take the fresh carbon in the envelope to the central core.The large He/H ratio can be reproduced by rotational mixing which can bring the helium from the core to the surface.Furthermore,the nonspherical structure implies that the star had a strong aspherical wind,probably because of rapid rotation at the phase of RSG.
In contrast to single stars,the enrichment of N/C and helium in the primary star can attain a higher value and heavily depends on the orbital period.For example,the quantityincreases from -0.53 to 2.14 for model B1 while it goes up from -0.53 to 1.92 for model B3.Therefore,nitrogen enrichment can attain the highest value during the first episode of RLOF in the tightest system B1.The main reason is that the hydrogen burning shell can be exposed early because more of the hydrogen envelope can be extremely stripped by RLOF.The rotating binary system B7 can reach a larger value of nitrogen before RLOF due to the efficient rotational mixing.At the end of evolution,the quantitydecreases rapidly because the carbon can be produced by 3α in the bare helium core.Moreover,nitrogen can be depleted by the nuclear reaction
3.5.The Evolution of the Helium Core Mass
Figures 4(c)and(d)illustrate that the helium core varies with time for an isolated star and a binary system with various orbital periods.Single star models suggest that SNe IIb arise in stars of modestly low mass,about <20 M⊙solar masses.A more massive initial star can give rise to a larger helium core(>6.0 M⊙).This provides us a clear clue of the initially low mass of the progenitor in the binary system because the mass of the collapsing core is only several solar masses.Moreover,the thick hydrogen envelope of low-mass stars must be removed by mass transfer via RLOF.Regardless of a single or binary star,rotation can significantly increase the helium core mass because the convective core at the stage of the main sequence can be significantly enlarged by rotational mixing.As the hydrogen shell burning surrounding the core consumes hydrogen and produces the helium ash falling to the core,the helium core mass grows slowly.However,the development of the helium core can be greatly restricted by RLOF because the hydrogen burning shell may be extinguished or eliminated by mass transfer via RLOF.The tighter the binary system is,the smaller the helium core mass.This indicates that the helium core of model B1 is most affected by the RLOF.
Actually,the helium core mass can essentially determine the type of SN events.The light curve of SN 1993J was fitted well by the model with an explosion of a helium core mass of 4–5 M⊙and a residual low mass hydrogen envelope(of around 0.2 M⊙)(Nomoto et al.1993;Woosley et al.1993,1994).The low mass progenitor with a radially extended~500 R⊙hydrogen envelope is required to give rise to the initially sharp peak in the light curve and this qualitatively explains the transformation of the spectral evolution from an SN II to an SN Ib.
The timing of the second SN peak of the light curve imposes an important constraint on the helium core mass.More massive helium stars reach the light curve maximum at later times because the heat produced by radioactive decays takes a longer time to diffuse out.The wind mass-loss rate of a single main sequence mass ≥30 M⊙is large enough to remove the hydrogen envelope and this star can generate an SN IIb(Heger et al.2003;Georgy et al.2009).However,this type of star has a helium core mass ≥8 M⊙previous to the explosion.An 8 M⊙helium core is too massive to produce the second maximum at~20 days as observed for SN 2011dh,even assuming the most extreme56Ni mixing (Bersten et al.2012).As a result,the helium core mass region of SN IIb is about 2.0–6.0 M⊙which has been listed in Table 2.
Our model suggested the primary with an initial mass about 16 M⊙turns into a helium core-burning RSG.It fills its Roche lobe and transfers about 10 M⊙during RLOF.A part of the remanent hydrogen envelope can be eliminated by strong stellar wind.
3.6.The Evolution of the Rate of Mass Transfer
Figure 5(a)shows the rate of mass transfer via RLOF varies with evolutionary time in the binary systems B1,B2 and B4.As matter flows from the more massive star to the less massive companion star in model B1,the orbital separation becomes short.The transfer of an amount of mass leads to shrinkage of the donor radius,moving it back within its Roche lobe.Moreover,the shrinkage of the Roche lobe of the primary indicates that it can transport mass at a maximum rate of~2×10-4M⊙yr-1(see Figure 5(b)).Due to this high rate of mass transfer,the thermal equilibrium is broken.The orbital separation stops shrinking when the star becomes the less massive of the two.From then on,continuing mass transfer will increase the orbital separation.The primary star,which remains on the main sequence,is still filling its Roche lobe so matter keeps flowing to the secondary,albeit at a lower rate<3×10-6M⊙yr-1.At the evolutionary age of 9.6 Myr,the primary has lost about 7.33 M⊙so M1=8.67 M⊙and M2=17.53 M⊙.Therefore,the rate of mass transfer has been decreased to the nuclear timescale of the primary.The mass transfer ceases at the end of the main sequence because the stellar radius shrinks briefly.At the subsequent hydrogen shell fusion phase,the star expands again and the resulting highmass transfer rate~4×10-4M⊙yr-1happens in the Kelvin–Helmholtz timescale.
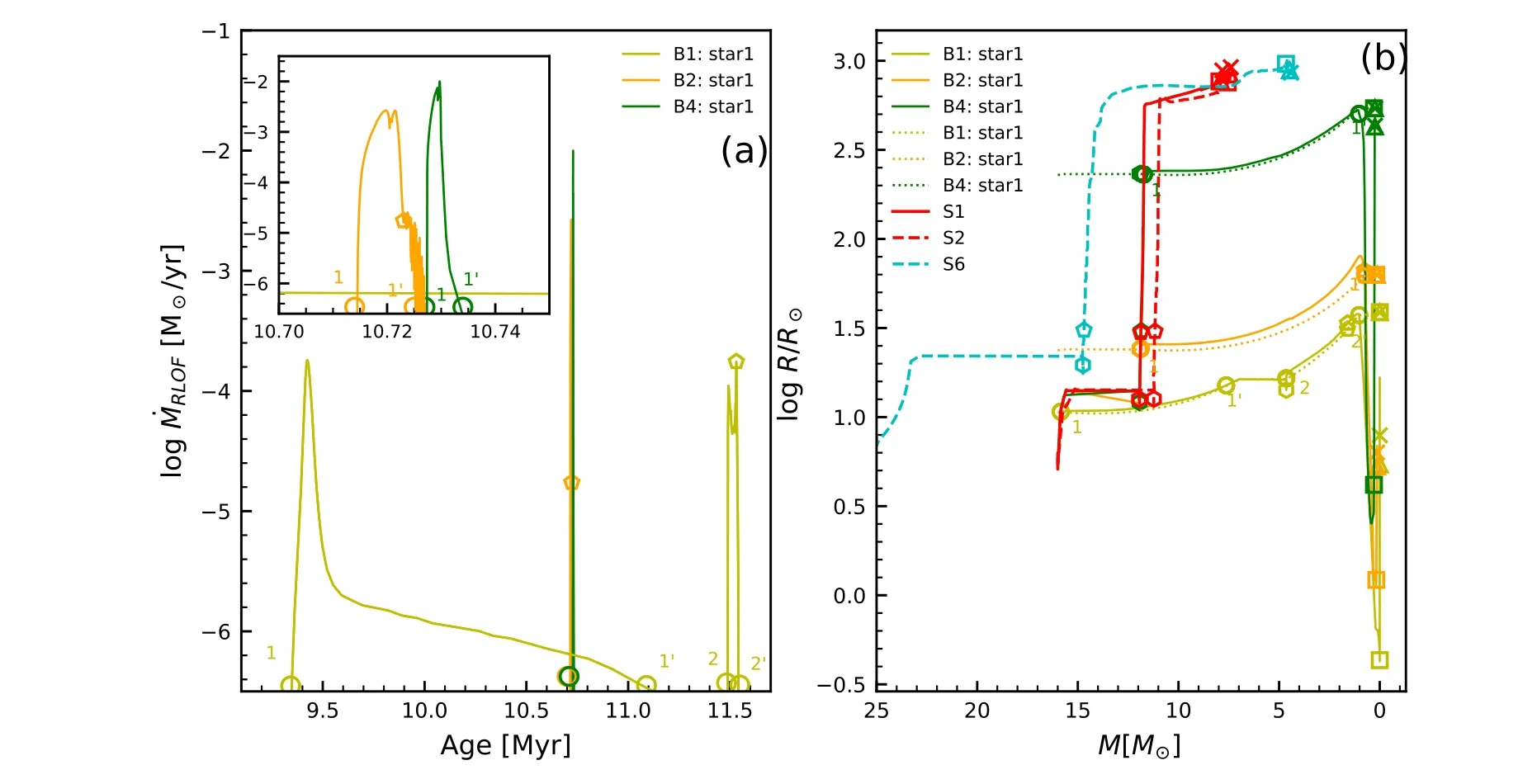
Figure 5.(a)The rate of mass-transfer via RLOF varies with evolutionary age in models B1,B2 and B4.(b)The variation of stellar radius with its stellar mass in the single and binary models.The dotted lines correspond to the Roche lobe in three binary models.
The primary in model B2 fills its Roche lobe during the hydrogen-shell fusion phase when it crosses the Hertzsprung gap.Then it starts to transport matter to the companion star.The expansion of the primary occurs on the Kelvin–Helmholtz timescale.As the orbit shrinks,this brings about a higher rate of mass transferin contrast to model B1 and a steep drop in luminosity in the HR diagram.The reason is that the mass transfer is so rapid that the star deviates from thermal equilibrium.Simultaneously,the central core cannot produce enough nuclear energy to keep pace with the expansion of the envelope,so the luminosity of the star drops dramatically during RLOF.
When the donor in model B4 evolves on the Hayashi line,mass transfer occurs.The rate of mass transfer is expected to be unstable because the RSG star has developed a deep convective envelope.This will lead to rapid shrinking of both the orbital separation and the size of the Roche lobes,while the donor star keeps expanding.This results in a very high rate of mass transfer of~1.0×10-2M⊙yr-1and thus the companion has no time to adjust.The mass transport flows in the dynamical timescale.Unstable mass transfer via RLOF generally results in the formation of a common envelope but the model B4 does not.The main reason is that the high initial mass ratio M2/M1can cause the system to avoid this phase.The accretion process happens after the secondary star has left the main sequence.This will increase its total envelope mass relative to its core mass.The secondary star is more likely to burn helium as BSGs instead of RSGs.The secondary star may explode as a BSG just like SN 1987A.One can find in Figure 1(b) that the binary system with the orbital period range of 110 days <Porb<720 days can evolve into observable RSG (i.e.,progenitors of SNe IIb.Rotation can shift the region of the orbital period toward the higher value because it tends to increase the mass loss.The effect of rotation on the range of the initial orbital period will be discussed in future work.
The less massive single star(i.e.,<~25 M⊙)ends its lifetime as an RSG (see Table 1) while the more massive single one(i.e.,>~25 M⊙) evolves into yellow-BSGs.Yellow or BSG progenitors can be produced by strong mass losses occurring at the stage of RSGs.For example,the high mass loss can be triggered by the interaction between radiation and dust.Rotational mixing enhances the stellar luminosity and thus favors a more efficient mass loss.Also yellow/BSGs may be produced by RLOF in a binary channel.In this binary case,RLOF does not necessarily merely happen at the RSG stage.It can occur at an earlier phase.A very good example is given by the case of SN 2011dh.The observations indicate that SN 2011dh is a YSG which represents a great challenge to the evolution of the isolated star.If the progenitor star were a single star,for it to attain the pre-SN state as a YSG,it would have suffered from a very strong stellar wind.The evolutionary track is very sensitive to the stellar wind and the RSG wind needs to be increased enormously.If the progenitor of SN 2011dh is a member of the binary system,we can naturally explain the main observational features of this star without increasing the stellar wind.
3.7.The Evolution of Stellar Radii
Figure 5(b) shows that the stellar radius changes with the evolutionary age for isolated stars and the primary stars in binaries.The radius goes up slightly during the core hydrogen burning.The more massive star S6 has a larger radius because the mass–radius relationship scales as R ∝M0.46at Z=0.02.In contrast to the non-rotating counterpart S1,rotation can help the star attain a larger size in model S6.The reason is that the centrifugal force becomes stronger at the equator than the pole.The star becomes oblate and the mean radius increases accordingly.When the single star crosses the Hertzsprung gap before core helium ignition,it swells dramatically.It tends to expand slightly after helium core burning.The radius of single stars can attain a maximum value of~103R⊙.One can notice that the total amount of mass loss is larger at the stages of both main sequence and RSG.This is because the lifespan of core hydrogen burning is the longest during the whole evolution.Moreover,the stellar wind of RSGs can attain a high value of~10-5M⊙yr-1.
The evolution of radius in the binary has two important features.First,the radius is constrained within the Roche lobe and is smaller than the single counterpart.The radius of the Roche lobe strongly depends on the orbital separation between two components and is less correlated with mass ratio.Thus,the shorter the initial orbital period is,the smaller the constrained stellar radius in the Roche lobe.Second,the radius expansion is non-monotonic and is followed by a contraction and re-expansion phase.This feature is associated with the process that the primary star attempts to restore thermal equilibrium after RLOF.In order to enter the observed effective temperature range (i.e.,3.6 and 4.1 in logarithm) of an SN IIb progenitor,the hydrogen envelope mass must be between 0.033 and 0.5 M⊙.SN 1993J and SN 2013df are RSG type SNe IIb and their radii are~600 R⊙.The corresponding hydrogen envelope mass is MH=0.2–0.4 M⊙.SN 2011dh (YSG progenitor,~200 R⊙) has a mass of hydrogen envelope of MH~0.1 M⊙while SN 2008ax (BSG progenitor,30–50 R⊙)has a mass of hydrogen envelope of MH~0.06 M⊙(Yoon et al.2017).This indicates that when the hydrogen envelope mass of the progenitor falls down,its radius decreases accordingly.The star become hotter and more compact.The mass of the residual hydrogen in the stellar envelope is clearly continuous,which also indicates the continuous transformation of the associated types of SN IIb progenitors from RSG and YSG to BSG.
We see large differences between an initially tight model B1 and a single star model S1 in the last evolutionary phase.The radius of the single model S1 can attain a maximum of 870 R⊙whereas it reaches 7.94 R⊙in model B1.The smaller radius of the SN progenitor implies that the star might be a component star in the binary system.The radius of an SN IIb covers the range from~50 R⊙of the BSG progenitor to~600 R⊙of the RSG progenitor.
The mass-loss rate prior to the explosion of SN IIb contains important information about their the associated evolutionary paths.The mass-loss property is reflected in the density of circumstellar matter.Maeda et al.(2015)noticed that there exists a close relationship between the progenitor radius and the average mass-loss rate shortly before the explosion.They reported that more extended progenitors (~600 R⊙;e.g.,1993J,2013df) have a very large mass-loss rate of~10-5M⊙yr-1before the explosion,while less extended progenitors(~200 R⊙;e.g.,SN 2011dh) have a moderate mass-loss rate(~3×10-6M⊙yr-1).Ouchi &Maeda (2017) explained that less extended progenitors have not only a smaller envelope mass to transfer but a larger value of equilibrium index ξeq.The larger ξeqmeans that the progenitor shrinks faster in response to the mass loss.However,mass loss rates can attain as high as~10-4M⊙yr-1from some RSGs which have been reported(van Loon et al.2005).It may also be possible that this extensive mass loss for the more extended progenitors can be explained by an RSG with strong stellar winds after RLOF in our models B4 and B8.In model B4,the radius of the primary has a value of 426 R⊙and its stellar wind is 2.58×10-5M⊙yr-1(RSG progenitor of SNe IIb).In the theoretical model B3,the radius of the primary has a value of 223 R⊙and its stellar wind is 3.4×10-6M⊙yr-1(YSG progenitor of SNe IIb).These theoretical results from model B4 are approximately consistent with observations of the SN IIb SN 1993J (see Table 2).
4.Conclusion and Summary
SNe IIb can be produced by stellar winds but the intensity of stellar winds needs to be well regulated.Therefore,it is very difficult for the less massive star(i.e.,<20 M⊙)to give rise to an SN IIb.Mass transfer in a binary system provides an alternative channel for mass loss.Interacting binaries can naturally interpret the presence of relatively low-mass SNe IIb.In particular,a binary evolutionary channel might allow the formation of yellow or BSG stars to originate from relatively less massive stars.In order to enter the observed effective temperature range between (in logarithm) 3.58 and 3.8 of the progenitor,the hydrogen envelope mass must be located in the range between 0.033 and 0.5 M⊙.A 16 M⊙primary with a 14 M⊙companion in a binary system with an initial orbital period range of 10 days <Porb<720 days can evolve into the observed range of SNe IIb.The type of the progenitor(i.e.,BSG,YSG and RSG progenitors of SN IIb) is closely related with the initial orbital period.The BSG type SN IIb progenitor originates from a system with an initial Porb~10 days while the YSG progenitor evolves from a system with an initial Porb~100 days.The RSG progenitor is from a system with 300 days <Porb<700 days.An initially tighter system leads to a larger peel of the hydrogen envelope via RLOF.With decreasing mass of the hydrogen envelope,the radius of the progenitor shrinks accordingly.The star becomes hotter and more compact.
It is extremely difficult for a system with an initial orbital period of Porb>700 days to produce an SN Ib/c without a hydrogen envelope (or even an SN IIb) in our RLOF scenario because the residual hydrogen envelope is sufficiently large.The star can maintain the RSG structure and explode as an SN IIP.However,other evolutionary channels (i.e.,CEE) or mass transfer implementations might change the evolutionary state in the initially wider system.It might be possible to reproduce the large radii SNe IIb in some other codes which have employed different physical factors or processes.This study is beyond the scope of this paper which focuses on the progenitor evolution of SN IIb via our RLOF scenario.Case B/A mass transfer in this orbital region can make the helium core be covered with a small amount of hydrogen envelope.Because the duration of Case B/C mass transfer is very short,a thick hydrogen envelope of MH>0.033 M⊙can be retained in the envelope.The envelope mass is larger than the one which is calculated from the binary model B1.Such a primary star may ultimately blow up as a type SN IIb SN 1993J,with a much extended envelope (1013–1014cm).Case A mass transfer in model B1 can produce an SN Ib because its hydrogen envelope is absent.
Rapid rotation can produce three favorable conditions to generate SNe IIb.First,rapid rotation can enlarge the helium core mass significantly and thus reduce the hydrogen envelope mass accordingly.Second,rotation can shift the lower limit of the initial orbital period which can produce SN Ib to a higher value because the centrifugal force tends to increase the mass loss via stellar winds.For a rapidly rotating component in the binary system,less hydrogen envelope mass,therefore,needs to be removed by the RLOF.Finally,rapid rotation significantly affects the stellar radius.Moreover,the transformation between spin angular momentum and orbital angular momentum can slightly affect the orbital separation and the size of the Roche lobe.These variations have a very important impact on the rate of mass transfer via RLOF because the mass transfer rate is closely related to the excess radius (i.e.,the difference between the stellar radius and the Roche lobe).
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant Nos.11863003 and 12173010),Science and technology plan projects of Guizhou province(Grant No.[2018]5781).Dr.Y.Qin gratefully acknowledges the Science Foundation of University in Anhui Province(Grant No.KJ2021A0106) .We are very grateful to ananonymous referee for his/her valuable suggestions and very insightful remarks,which have improved this paper greatly.
杂志排行
Research in Astronomy and Astrophysics的其它文章
- Discovery of Extended Structure Around Open Cluster COIN-Gaia 13 Based on Gaia EDR3
- Constraining Brans-Dicke Cosmology with the CSST Galaxy Clustering Spectroscopic Survey
- The First Photometric Study of AH Mic Contact Binary System
- Detections of Gamma-Rays from Globular Clusters ESO 452-SC11,NGC 6380,Palomar 6 and UKS 1 with Fermi-LAT
- Crust Cooling of Soft X-Ray Transients-the Uncertainties of Shallow Heating
- Quasi-periodic Oscillation Analysis for the BL Lacertae Object 1823+568
