公路钢桥正交异性钢桥面板抗疲劳设计研究

摘要 钢结构具有容重小、韧性好的优点，在桥梁工程中有着十分突出的应用优势，但在长期荷载循环作用下，同时受到焊接应力、截面变化等的影响，很容易导致疲劳破坏的发生，甚至还会引发结构断裂。因此，针对钢结构桥梁展开疲劳研究尤为重要。文章以我国某桥梁工程为例，借助ANSYS有限元分析软件对其正交异性钢桥面板展开了疲劳分析。结合计算及分析结果，从疲劳设计准则、疲劳细节分类以及疲劳荷载三个层面展开研讨，为我国桥梁工程的技术完善提供理论支持。

关键词 公路钢桥;正交异性钢桥面板;疲劳设计

中图分类号 U443.31文献标识码 A文章编号 2096-8949（2022）09-0111-03

引言

钢结构是我国基础工程建设的重要材料，尤其是在桥梁工程中应用广泛，决定着结构强度、耐久性等多项重要指标。但受到焊接施工、加工工艺等的影响，疲劳问题是桥梁设计必须考虑的一项因素[1]。在桥梁设计中，正交异性钢桥面板不仅可以直接承载上部荷载作用，同时也能与主梁形成良好搭接共同工作，表現出材料用量省且工程性质稳定的优点。但受构造要求及焊接效应的影响，长期使用状态下纵肋与面板交界位置很容易产生开裂[2]。针对这一问题，着力于改善桥面抗疲劳能力，优化抗疲劳设计尤为关键，具有突出的应用价值。

1 工程实例概况

该文以我国某桥梁工程为例，采用正交异性钢桥面板纵向U肋与顶板焊接、横隔板与U肋焊接处典型疲劳细节。按照现行疲劳规范完成设计与验算，比对不同标准疲劳车辆下面板内所产生的损伤情况。

主梁选用单箱三室箱形截面钢箱梁，标准段长10.5 m。顶板及底板宽度分别为29.5 m、17.5 m，主桥中心线位置的箱梁高3.5 m。在箱梁内设计有两块腹板，设计间距为1.7 m。

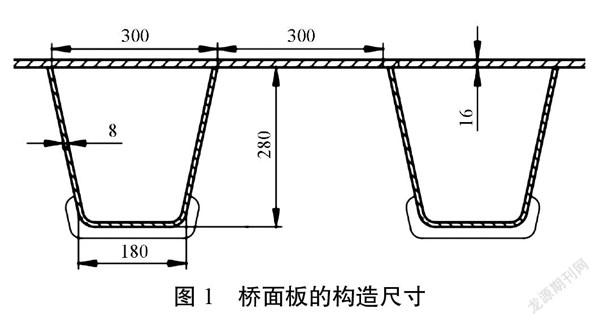
各箱梁段内分别留有三道横隔板，其中两侧横隔板分别距梁端1 m、2.5 m，三道横隔板的间距定为3.5 m。正交异性钢板各尺寸如图1所示，箱梁隔板选用实腹式设计，且有普通横隔板和端横隔板两类，厚度均为12 mm，加劲肋厚度均为10 mm。

2 建立有限元分析模型

该文借助ANSYS有限元分析软件建立计算机模型进行分析[3]，分析对象选为两个长度为21 m的标准钢箱梁，考虑到箱梁截面沿桥轴线中心呈中心对称，因此设定1/2截面面积。模型中所有构件均使用三维板壳单元Shell63模拟，钢材为Q345钢，弹性模量为206 GPa、泊松比选为0.3。该模型整体划分为了92 898个单元，在对称界面上附加对称约束，两侧仅释放绕X方向的扭转约束，模型荷载根据车辆单轴重量及接地面积进行计算。

3 疲劳荷载施加及计算工况

对A、B、C点的疲劳强度进行验算，应当先得出疲劳荷载作用下这些位置各自的应力幅值，并基于最大拉、压应力所对应的加载点确定最不利加载位置。所以，在确定位置时就需要反复调整使得疲劳车辆在纵向及横向上移动。已有的研究表明受到车轴直接作用时，正交异性钢桥面板的关键疲劳细节都会达到最大值，且当车轴远离时将快速下降。

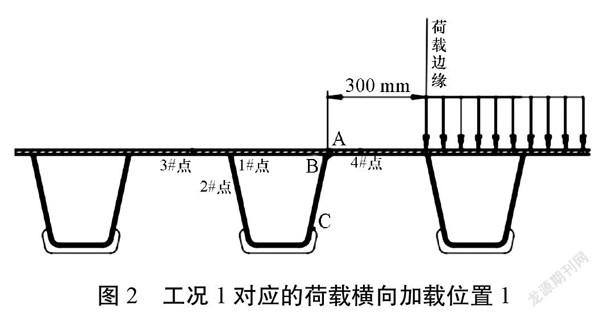
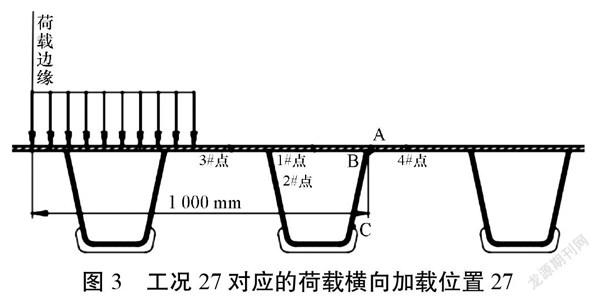
不同地区对于疲劳车辆的规范要求不尽相同，因此在确定轮压面积、轴距等基本参数时也将依照不同的标准，由此测得的A、B、C点最大应力加载位置也就不可避免地存在一定偏差。在确定各个关键节点的应力状态时需要把握疲劳车辆的影响规律，灵活调整测量方法。将A点作为测量原点，且以A点右侧作为正方向，控制疲劳车辆在横向?1 000～300 mm的范围内移动，移动步长以50 mm为标准，由此总共可得27个不同的计算工况[4]。图2及图3分别为第1个工况和第27个工况。记录下疲劳车辆移动过程中A、B、C及其他关键点的应力水平变化，得到各点应力与横向位置之间的关系并绘制相应图表。

基于A、B、C三点与纵向位置的关系曲线即可确定疲劳车辆最不利的加载位置。将A点作为测量原点，车辆移动控制在?500～1 500 cm的范围内，并记录A、B、C三点的应力水平，根据分析结果得到各点应力与纵向位置之间的关系并绘制相应图表。最后即可在基础上计算得到A、B、C三点的最大应力幅。

4 计算结果分析

4.1 各关键点受力对比分析

有限元分析发现，比对时以A点作为原点建立坐标系，疲劳车辆与A点之间的相对位置作为X轴，各关键点的应力水平作为Y轴。

4.1.1 1#点应力水平对比

对不同疲劳车辆位置下1#点的横、纵向应力水平变化作为研究对象展开分析，主要工况条件下的应力分析值如表1所示。1#点所对应的X坐标为?300。

在疲劳车辆的移动下，1#点的应力水平发生了较为明显的变化，且在X=?400位置出现了最大压应力值，其横向压应力峰值与纵向压应力峰值分别为?33.80 MPa、?15.73 MPa。而在当X800或X0时的区段内，1#点的应力则呈现出不断下降的趋势。在疲劳车辆不断移动过程中，1#点大多数都处于受压状态下，只在0～300的区段内存在部分拉应力，拉应力在X=0位置处达最高水平，横向拉应力峰值与纵向拉应力峰值分别为2.68 MPa、0.96 MPa。

4.1.2 2#点应力水平对比

对不同疲劳车辆位置下2#点的横、纵向应力水平变化作为研究对象展开分析，主要工况条件下的应力分析值如表2所示。2#点所对应的X坐标在?250～?300的区间内。

疲劳车辆移动过程中2#点应力水平的变化与1#点比较类似，都大致为曲线关系。竖向应力的最小值在X=?500位置附近出现，约为?10.74 MPa;而最大值在X=0位置附近出现，约为0.57 MPa。同时纵向应力的最小值在X=?400位置附近出现，约为?3.62 MPa;在X800或X0的区段内，2#点的应力则呈现出不断下降的趋势。根据不同疲劳荷载位置下1#与2#点的应力变化趋势可以得出，车轮轮压作用于纵向U肋腹板位置处时其受力最为不利。

4.2 A、B、C点应力水平对比

4.2.1 A点应力水平分析

不同横向荷载作用位置下A点应力幅的变化趋势与1#点基本类似。横向、纵向应力的最大值均在X=?300位置附近出现，是结构最为不利的状态。所以，可将X=?300 mm定为疲劳车辆作用的最不利横向位置。将A点作为分析原点，当疲劳车辆位于?300～1 500 cm的区段内以20 cm作为行驶步长移动时，疲劳荷载作用于A点所产生的应力要远高于作用于其他位置时。当作用点与A点间距大于1 m时，应力则处于接近于0的水平，当作用点位于A点上时，应力达到最大水平，这也表明A点处的纵向影响线比较短。

4.2.2 B点应力水平分析

B点表征着正交异性钢桥面板纵向U肋与顶板之间的焊缝位于U肋焊趾处的疲劳细节[5]。分析结果表明，这一位置发生疲劳破坏的形式大多为焊趾的纵向开裂，且可将裂缝分布方向与竖向正应力看作近似垂直。

B点竖向应力最大值出现在X=?600 mm的位置附近，所以，可将X=?600 mm定为疲劳车辆作用的最不利横向位置。将B点作为分析原点，当疲劳车辆位于?500～

1 500 cm的区段内以20 cm作为行驶步长移动，其他布置与A点相同，发现疲劳荷载作用于B点所产生的应力要远高于作用于其他位置时的水平。当作用点与B点间距大于0.3 m时，应力则处于接近于0的水平，当作用点位于B点上时，应力达到最大水平。

4.2.3 C点应力水平分析

C点表征着正交异性钢桥面板横隔板与纵向U肋焊接端部的疲劳细节。这一位置存在比较严重的应力集中与初始缺陷问题，在较高水平荷载作用下容易产生疲劳裂纹，裂缝分布方向与主应力基本垂直。由计算可以得知C点处的横向应力xσ相较于竖向应力yσ与纵向应力zσ较小，为简化分析可不纳入考虑范围。

C点竖向、纵向应力最大值出现在X=?200 mm和X=?700 mm的位置附近，所以可分别将X=?200和X=?700 mm定为疲劳车辆作用的最不利横向位置。将C点作为分析原点，当疲劳车辆位于?600～600 cm的区段内以20 cm作为行驶步长移动时，疲劳荷载作用于C点直至破坏的循环次数比A点更多，导致这一现象的原因在于横隔板处影响线比较短，在循环荷载作用下循环次数就会更多。

5 结束语

该文以我国某工程案例为基础展开分析，借助有限元分析法计算分析了结构的受力特点及疲劳强度，得到主要结论有：

（1）对1#和2#两个不同关键点的分析可以发现，1#点分析得到的应力幅远高于其他关键点，且同时伴随产生应力集中问题;1#关键点的横、纵向正应力与恒载横向位置之间存在明显的线性相关性。当横向荷载作用在A点位置时，2#点才受到荷载作用的影响，而当X=?800，横向荷载的影响则十分微弱。当荷载作用位置从X=?300靠近时，2#点的应力水平处于不断上升的状态，且在X=0位置达到峰值;当荷载作用位置从X=?800向远离2#点方向移动时，2#点处应力可视为0。

（2）对细节A、B、C及主要关键点的疲劳强度分析可以得出正交异性钢桥面板顶板与U肋焊缝的焊趾、横隔板与U肋焊接处的疲劳细节的横向、纵向影响线均很短。这些位置在疲劳荷载作用下表现出十分突出的敏感性，应力幅比较大，是疲劳裂纹的高发位置[6]。由于横隔板与U肋焊接处疲劳细节影响线比U肋与顶板焊接处疲劳细节影响线更短，所以在疲劳荷载下C点的循环次数明显高于A、B点，且其应力变化趋势也更缓。

参考文献

[1]屠义伟， 赵际军. 大纵肋钢桥抗疲劳设计方法研究[J]. 公路工程， 2019（3）： 69-73.

[2]张清华， 卜一之， 李乔. 正交异性钢桥面板疲劳问题的研究进展[J]. 中国公路学报， 2017（3）： 14-30+39.

[3]李芹子. 公路鋼结构桥梁抗疲劳设计方法研究[D]. 西安： 长安大学， 2014.

[4]韦伟， 陈齐风. 轮载下钢桥正交异性桥面板疲劳应力分析[J]. 西部交通科技， 2015（10）： 41-46.

[5]黄祖慰， 雷俊卿， 桂成中， 等. 斜拉桥正交异性钢桥面板疲劳试验研究[J]. 浙江大学学报（工学版）， 2019（6）： 1071-1082.

[6]李自林， 连延金， 刘治德. 公路桥梁正交异性钢桥面板关键部位疲劳应力分析[J]. 铁道建筑， 2013（11）： 13-15.

收稿日期：2022-01-14

作者简介：刘冉（1988—），男，本科，工程师，研究方向：道路桥梁工程设计。