基于问题式教学的高中数学教学案例探究

郭嘉祥

(福建省漳州市第三中学 363000)

高中新课程标准(2017版)的实施，人教版高中新教材(2019版)的使用，信息技术与学科教学的深度融合，对教师的教学方法提出了更高的要求，以学生为主体的问题式教学法在课堂教学中被广泛采用.问题式教学法是教师按本节课的教学目标和教学内容，设计出一系列相互关联的问题串，通过这些问题串来引导学生进行课堂学习，学生通过思考、小组讨论、解答问题，总结、掌握知识点，完成教学目标.教师对问题设计的好坏，是问题式教学有效与否的关键，因此，笔者以几个教学案例，谈谈问题式教学过程中问题串的设计思路.

1 通过问题设计引导学生探究新知识

高中数学有很多知识的研究方法是相似的，教师可以通过问题设计让学生类比之前的学习方法进行自主探究.例如《对数函数的图象与性质》一课，学生已学习过函数的图象和性质，并且通过《指数函数的图象与性质》一课的学习，掌握了研究指数函数的图象与性质的方法，于是，笔者设计了以下问题，引导学生进行类比探究.

问题1：同学们，我们学习过函数的哪些性质？

问题2：如何研究函数的这些性质？

问题3：回顾一下指数函数图象与性质的研究过程？

问题4：类比研究指数函数图象与性质的方法，我们应该如何研究对数函数的图象与性质？

追问4.1：先画哪几个具体的对数函数图象？

追问4.2：这些对数函数图象有哪些关联？你能画出一般的对数函数图象吗？

追问4.3：观察图象，对数函数有哪些性质？

问题5：对比指数函数与对数函数的图象与性质，有何异同点？

2 通过问题设计引导学生寻找新方法

上面的案例是类比旧知识的学习方法来探究新知识，笔者再举一个案例《正切函数的性质与图象》，则是不同于旧知识的学习方法，教师引导学生寻找新方法来探究相关联的新知识.在这节课之前，学生已经学过了正弦函数和余弦函数的图象与性质，研究方法是先图象再性质，但为了培养学生的学科素养，本节课并没有采用这种思路，而是先研究正切函数的性质，再作出图象，对这种研究顺序的改变，教学设计时就应辅于一定的问题串作为铺垫，帮助学生更顺利的进行探究.

问题1：同学们，今天我们将学习正切函数的性质与图象，但不同于我们之前学习正弦函数和余弦函数的图象与性质的研究方法，我们打算先研究正切函数性质，再研究正切函数图象，大家思考一下，如果先研究正切函数图象，有没有什么困难？

设计意图：让学生明白为什么没有采用以往常见的方法，先研究图象，再研究性质，其实是培养学生在遇到困难时要善于转换思路，寻找更快捷的方法来解决问题，为此，教师必须让学生了解先研究正切函数图象的困难在哪里，同时这样的设计也让学生对函数性质的研究方法有更深刻的理解.

问题2：既然我们先研究正切函数的性质，应该先研究什么性质？

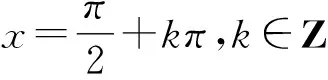
问题3：我们是如何研究正弦函数的周期的？你能类比研究正切函数的周期吗？

问题4：如何判断正切函数的奇偶性？

设计意图：类比正弦函数周期性和奇偶性的研究方法，即利用定义研究正切函数性质.

问题5：我们应该选择哪个区间来研究？这种选择对研究正切函数的图象及其他性质会有什么帮助？

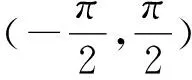
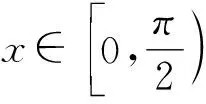
问题7：结合已得到的正切函数的周期和奇偶性，画出正切函数在定义域内的图象，观察图象，说说正切函数的图象有哪些特征？

问题8：利用正切函数的图象，你能归纳出正切函数的性质吗？

问题9：通过这节课学习，同学们能否归纳出研究正切函数的性质与图象的方法？获得关于正切函数的哪些基本知识、技能？在应用中有哪些经验？

设计意图：利用图象归纳性质是之前研究函数性质常用的方法，学生比较熟悉，所以教师在这节课的总结时要更关注数形结合思想的渗透.数学核心素养的培养就是要落实到平时的教学活动中，通过问题设计来提高学生的思维能力.

3 通过问题设计引导学生突破重难点

高中数学公式的推导往往比较抽象，令学生无从下手，如果教师只是把书本上的公式推导过程演绎给学生看，学生大多只是看懂了过程，记住了公式，但对于为何要使用这样的方式证明知之甚少，不利于培养学生的核心素养.例如《等比数列的前n项和》一课，如果教师只是采用从特殊到一般的思想方法，引导学生先求1+2+22+23+…+2n-1，再求一般等比数列的前n项和，那么学生往往会觉得很跳跃，也许能记住这种操作方式叫错位相减法，但对于为什么要同时乘以公比，在学习初期是比较茫然的.为此，笔者设计如下问题引导学生探索等比数列前n项和的求法，从中引出错位相减法.

问题1：通过实例，引出求和问题：1+2+22+23+…+2n-1.

追问1.1：观察这列数字的特点，是否为特殊数列？

追问1.2：类比等差数列前n项和的推导方法，能否采用倒序相加法求等比数列的前n项？

追问1.3：求前n项和的精髓是消项，对于等比数列，有没有办法出现相同项以达到消项的目的？

设计意图：学生之前刚学过等差数列的前n项和，常见的错误就是对于非等差数列求和也套用等差数列的求和公式，为此设计追问1.1，提醒学生在套用求和公式之前要注意数列的类型.既然等比数列不能套用等差数列的求和公式，那学生在寻找新的求和方法时，最先考虑的就是能否采用推导等差数列前n项和公式的方法，即倒序相加法，来求等比数列的前n项，为此设计追问1.2，不仅复习倒序相加法，也提醒学生注意，只有满足倒序相加法的适用条件，才能达到消项的目的.为了帮助学生寻找新的求和方法，教师再抛出追问1.3，让学生观察这个等比数列各项的特点，即从第二项起，每一项都是前一项的2倍，所以只要对这个等比数列的每一项都乘以2，就可以使前一项变成与原来的后一项相同，由此归纳出错位相减法.接着，利用从特殊到一般的思想方法，笔者又设计了问题2作为铺垫.

问题2：求1+q+q2+q3+…+qn-1.

问题3：求等比数列{an}的前n项.

设计意图：如果从问题1直接跳跃到问题3，学生探究起来是有难度的，而增设了问题2，既是对问题1进行了一般化，又提示了问题3的求和方法.

问题4：对于问题3中的错位相减法，能否将“同时乘以公比”改为“同时除以公比”？

设计意图：让学生进一步明确，求和的精髓是消项，错位相减法“同时乘以公比”的目的是消项，而“同时除以公比”也能达到消项的目的，同样是可行的.

通过这一系列的问题串，学生学到的不只是错位相减法这一种方法，学生会更清楚到的认识到错位相减法的目的是为了消项，将来遇到新的问题，学生会去寻找消项的方法，这样学生的思维就得到了拓展.

总之,问题式教学法是如今很流行的一种教学方法，也是我校数学教研组的特色，需要教师对课程标准和教材内容有深刻的理解，能根据学生的实际学情设计合适的问题串，引导学生在解决问题的过程中学习知识，提高学科素养.在今后的教学过程中，笔者也将继续探索，力图更好地将问题式教学法应用于课堂中.