含折线型裂隙砂岩试件翼型裂纹起裂与扩展机制研究

张 科，潘 哲，刘享华

（1.昆明理工大学电力工程学院,云南 昆明 650500；2.昆明理工大学建筑工程学院,云南 昆明 650500）

在漫长的地质构造作用下，岩石内部往往赋存着大量产状不同、性质各异的不连续结构面。在外部荷载作用下，这些结构面周围易产生裂纹起裂、扩展和贯通，进而威胁岩石工程的安全稳定性[1]。因此，研究含不同裂隙几何分布的岩石力学特性和断裂机制，已成为岩石力学与工程领域的重点问题。

学者们已对裂隙岩石的力学问题进行了系统研究，取得了卓有成效的成果。Wong 等[2]对含不同裂隙倾角的单裂隙岩石和类岩石试件进行室内试验，结合前人研究成果，更为系统地总结了7 种裂纹类型。郭奇峰等[3]采用单轴压缩试验研究了含单裂隙花岗岩的强度和破坏特征，发现裂纹起裂角随着裂隙倾角的增大而单调增大。罗可等[4]探索了加载速率对含单裂隙类岩石力学特性的影响效应，总结了峰值强度、峰值应变和弹性模量与加载速率之间的关系。还有学者采用数值方法研究了裂隙岩石的断裂机制。Zhang 等[5]构建平行黏结模型并对含单裂隙的岩石进行单轴压缩试验，基于矩张量方法区分初始裂纹和次生裂纹。Yang 等[6]、王星辰等[7]采用颗粒流数值研究了含2 条预制裂隙岩石的裂纹扩展过程，总结了应力-应变曲线、裂纹扩展以及裂纹数量之间的关系。随着监测技术的快速发展，任建喜等[8]结合CT 扫描技术，实时观测了含单裂隙岩石的变形破裂过程。张科等[9]结合数字图像相关方法追踪试件加载过程中应变场演化，并引入分异速率，识别翼型裂纹起裂时的异常前兆特征。张国凯等[10]采用声发射-声波一体化装置监测单裂隙岩石裂纹扩展规律，建立了裂纹扩展、贯通与声波及声发射之间的对应关系。

受限于传统的试件制备工艺，上述学者将自然裂隙形态简化为直线型，而在实际工程中，岩体内部赋存的裂隙普遍表现为非线性结构，如图1所示[11]。近年来有学者对含非直型裂隙岩石的力学特性进行了初步探索。Ma 等[12]以光敏树脂为打印基材，通过3D 打印技术打印含S 型裂隙的类岩石试件，并结合RFPA 数值模拟探究了裂纹扩展特征。朱栋等[13]在黄砂岩中预制弧形裂隙，研究了弧形高度和直径比值对试件力学参数、起裂形式和破坏形式的影响规律。王桂林等[11]通过PFC2D 数值模拟含Z 型裂隙试件的强度和变形破裂行为，将破坏模式分为张拉破坏、剪切破坏和拉剪复合破坏。刘新荣等[14]对含V 型裂隙砂质泥岩进行单轴压缩试验发现，随着裂隙夹角的增加破坏模式可分为台阶式拉剪复合破坏、八字形张拉剪切破坏以及台阶式剪切破坏。上述研究表明，非直线型裂隙试件的强度和变形破裂特征不同于直线型裂隙试件。而岩体内部的裂隙结构面往往表现为非光滑起伏形态，因此本文基于前人的研究设计了更接近工程实际的折线型裂隙。

图1 岩质边坡中的折线型裂隙[11]Fig.1 Folded fissure in a rock slope[11]

数字图像相关方法（digital image correlation method，DIC）是一种非接触式、全场变形测量方法，在裂隙岩石试验研究中得到广泛应用[9,15]。基于此，本文综合室内试验、DIC 方法和数值模拟，深入研究折线型裂隙裂纹起裂和扩展机制。对含直线型和含折线型裂隙砂岩进行单轴压缩试验，利用数字图像相关方法追踪裂纹起裂和扩展过程，根据位移场计算结果从细观力学角度揭示翼型裂纹形成机制。运用扩展有限元法（XFEM）对试验结果进行验证，并通过试件应力场分布特征解释裂隙形态对裂纹起裂位置的影响机制。研究成果有助于深入认识含非直线型裂隙岩石的断裂机制。

1 试件制备与试验过程

1.1 物理试件制备

本次研究选取红砂岩为研究对象，取自云南省禄劝彝族苗族自治县。岩块均匀致密，无明显宏观缺陷，自然状态下呈红褐色。将岩块切割成尺寸为长×宽×厚=120 mm×60 mm×20 mm 的长方体试件，采用高速水刀切割技术制备折线型裂隙，折线型裂隙试件的几何分布如图2（a）所示。裂隙中心与试件形心重合。裂隙长度l定义为裂隙两端点连线的长度，本文设置为24 mm。裂隙倾角α定义为裂隙两端点的连线与水平方向的交角。在许多工程实际中发现，缓倾角裂隙易诱发地质灾害[16]，故将裂隙倾角α设置为30°。裂隙起伏度β定义为裂隙终端边与裂隙两端点连线的夹角。目前，学者们系统地研究了压缩荷载作用下含不同几何分布特征的直线型裂隙试件变形破裂特征，但鲜有涉及裂隙起伏度的影响效应。已有学者[17-18]探索了剪切作用下含不同起伏度的裂隙力学特性，起伏度变化范围为10°～45°。借鉴前人的取值，本文将裂隙起伏度设置为20°。

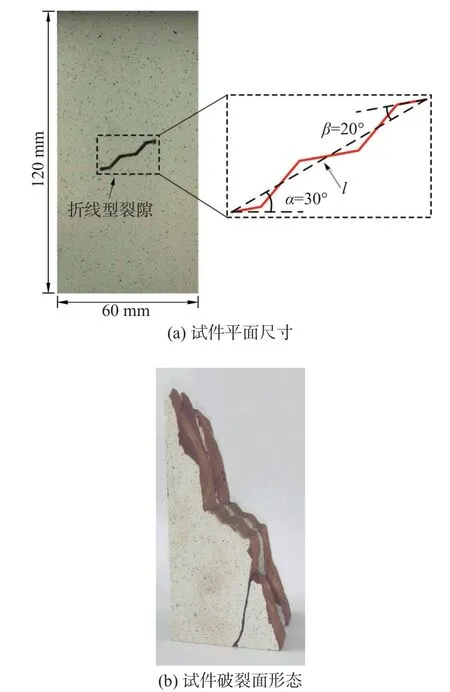
图2 含折线型裂隙砂岩试件示意图Fig.2 Sketch of the sandstone specimen containing a folded fissure

此外，还制备了含30°倾角的直线型裂隙砂岩用于对比分析，其裂隙长度l也设置为24 mm。制备含折线型、含直线型裂隙砂岩试件各2 块，试件编号规定为“试件类型-序号”，其中F 代表含折线型裂隙试件，S 代表含直线型裂隙试件，如“F-1”代表含折线型裂隙的砂岩试件1。试件几何参数见表1。

表1 砂岩试件几何参数Table 1 Geometric parameters of the sandstone specimen

1.2 数字图像相关方法

DIC 技术的原理如图3所示。假设试件变形前数字散斑图像的灰度特征值函数为I1=F1(x，y)，变形后为I2=F2(x，y)。首先在变形前的图像中选取1 个包含待测点P(x，y)的参考子区，然后在变形后的图像中按照预先给定的相关函数搜索与之匹配的目标子区，从而得到该测点的水平和垂直位移分量u、v[9,15]。

图3 数字图像相关方法的基本原理Fig.3 Principle of the digital image correlation method

在进行DIC 测试前，需要对试件观测面进行处理：首先对试件正面均匀喷涂1 层白漆，待其干透后，喷洒黑漆并使黑漆颗粒均匀地落在白漆表面，从而形成人工散斑场。

本次研究采用Ncorr 数字图像相关计算软件[9,15]，该软件集成子区变形、互相关系数、非线性优化和可靠性引导等算法，计算高效、准确，已广泛应用于岩石力学测试。将试验过程中采集的数字散斑图像导入Ncorr 软件，以加载初始时刻的数字散斑图像作为参考，计算试件变形破裂过程中的水平应变场(εxx)和垂直应变场(εyy)。

1.3 数值试件

学者们常将岩板试件的力学问题简化为二维平面应力问题[19-20]，而试件正面和背面裂纹扩展形态几近相同（图2b），进一步说明这种简化的合理性。扩展有限元法（XFEM）是一种有效求解断裂力学问题的数值方法[21]，本文将其应用于模拟含直线型和折线型裂隙试件的翼型裂纹起裂与扩展过程。采用ABAQUS软件建立二维平面应力模型，数值试件尺寸为长×高=120 mm×60 mm，其预制裂隙布置方式与物理试件一致以保证模拟结果的可靠性。数值模型材料的基本物理力学参数为：密度ρ=2 380 kg/m3，弹性模量E=7.08 GPa，泊松比v=0.3，抗拉强度σt=7.51 MPa。采用四节点双线性平面应力四边形单元进行网格划分，共划分13 998 个单元。选择最大主应力准则作为破坏判据，通过裂纹面水平集函数追踪裂纹扩展路径[21]。

1.4 试验装置和试验结果

试验装置如图4所示。单轴压缩试验设备采用WDW-100E 万能试验机，最大试验力100 kN，精度±0.5%。采用位移控制加载，加载速率设置为0.3 mm/min，加载至试件破坏。试件上、下两端涂抹凡士林以减少摩擦效应。利用CCD 工业相机（2592×1944 像素）实时记录试件正面的数字散斑图像。试验开始前，将加载设备和采集系统的时间同步。

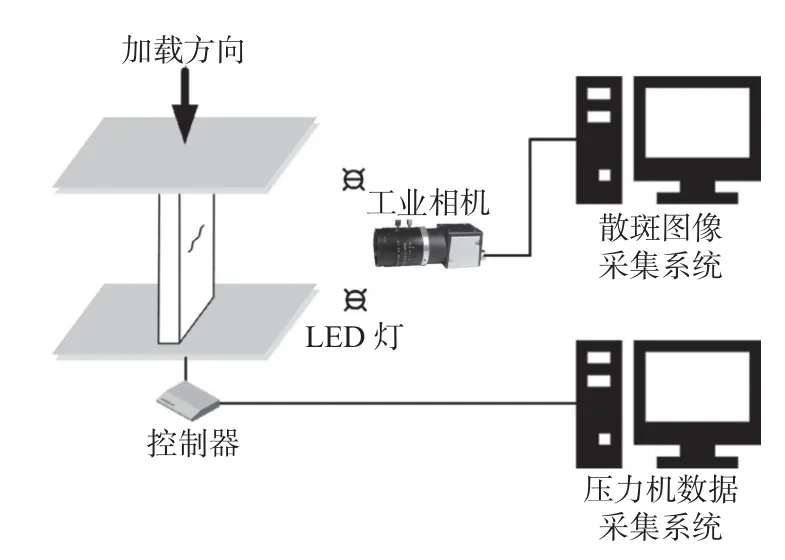
图4 试验装置Fig.4 Experimental setup

直线型裂隙和折线型裂隙试件的典型应力-应变曲线如图5所示，这2 种试件的变形破裂过程大体相同。应力-应变曲线中的A、B和C对应不同的应力水平，下标“S”和“F”代表试件类型。其中，标记点AS(σ/σc=0.58)和AF(σ/σc=0.52)对应翼型裂纹起裂点，标记点BS(σ/σc=0.72)和BF(σ/σc= 0.78)对应着翼型裂纹扩展，标记点CS(σ/σc= 0)和CF(σ/σc=0.02)对应试件最终破坏。

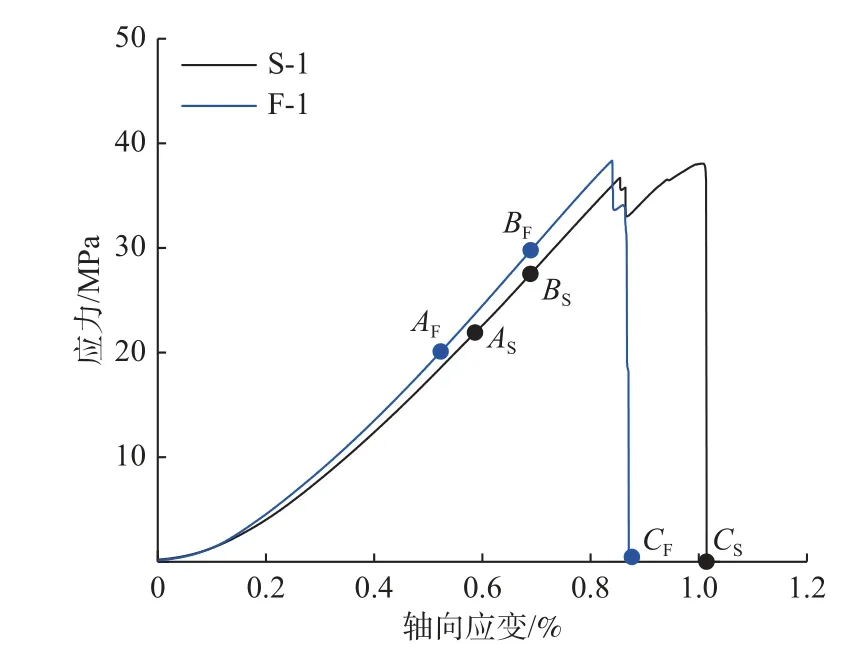
图5 典型应力-应变曲线Fig.5 Typical stress-strain curves

各试件的力学参数统计结果如表1所示，其中σc和E分别代表单轴抗压强度和弹性模量。从表1 中可知，直线型裂隙和折线型裂隙试件的平均抗压强度分别为38.67，37.31 MPa，平均弹性模量则分别为5.71，5.16 GPa。各项力学参数的变异系数小于0.02，表明试件的力学性能离散性较小，均质性较好。

2 含裂隙砂岩裂纹扩展演化机制

2.1 裂纹起裂过程及其机制解释

对于含直线型裂隙砂岩试件，当加载至标记点AS时，预制裂隙尖端周围出现与裂隙近似垂直的翼型裂纹（图6a），记为T，这与前人的试验结果一致[22]。而对于含折线型裂隙试件，加载至标记点AF时，裂纹起裂位置位于靠近裂隙端部的折角处，新生裂纹近似向折角的角平分线方向起裂，如图7（a）所示。

结合DIC 计算结果可知，2 类试件翼型裂纹处的水平应变场均出现了应变局部化带，其水平位移场则出现了位移不连续，如图6（b）（d）和图7（b）（d）所示。从裂纹周围的水平位移分布还可以发现，左侧和右侧位移符号相反，发生相背运动，也会出现两侧位移符号相同，都为正，但右侧位移大于左侧，这2 种情况都说明翼型裂纹处于受拉状态，见图6（d）和图7（d）。

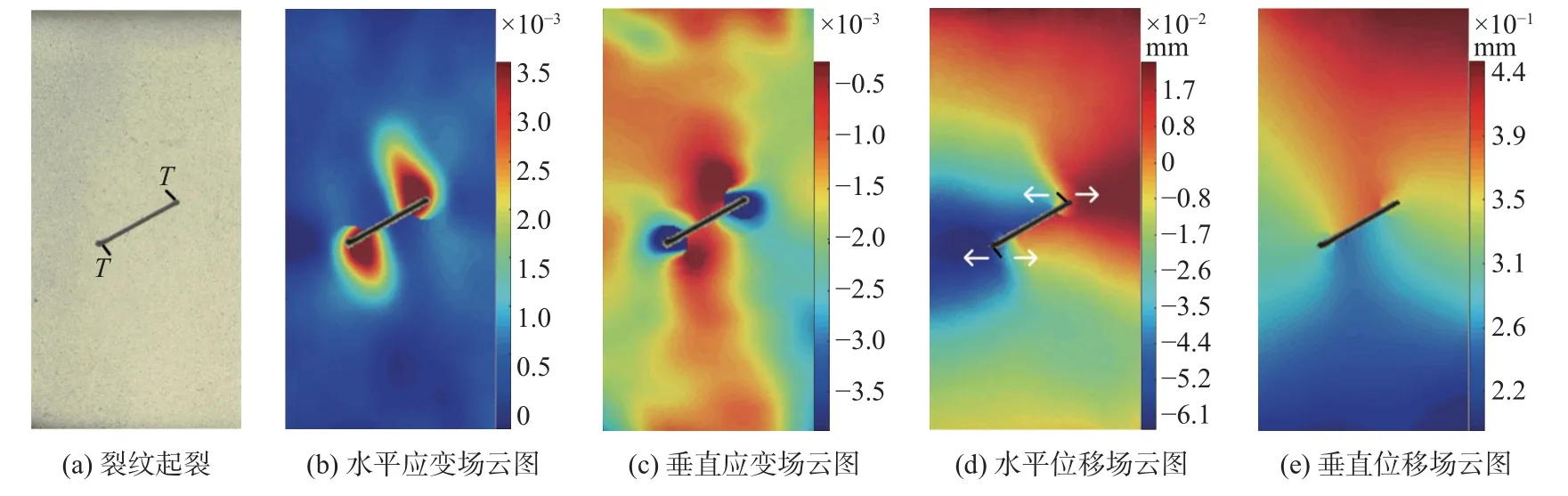
图6 含直线型裂隙试件裂纹起裂及变形场（标记点AS）Fig.6 Crack initiation and deformation fields of the specimen containing a straight fissure (Point AS)

图7 含折线型裂隙试件裂纹扩展及变形场（标记点AF）Fig.7 Crack initiation and deformation fields of the specimen containing a folded fissure (Point AF)

起裂应力是岩石力学性质的宏观体现，能够反映岩石的非均质性和结构差异。Yang 等[23]建议将宏观裂纹首次出现对应的轴向应力作为起裂应力，本次研究据此统计所有试件的起裂应力，结果如图8所示。从图8 中可知，含折线型裂隙试件的起裂应力小于含直线型裂隙试件，前者平均起裂应力为19.97 MPa，后者则为21.46 MPa。因此，相比于直线型裂隙，折线型裂隙的存在加剧了岩石非均质性。为探究这2 类试件起裂位置和应力差异的力学机制，采用ABAQUS 有限元软件计算数值试件的应力场。图9 为轴向位移0.04 mm 时的试件最大主应力云图以及局部放大图，软件规定拉应力为正。从图9（a）中可以看出，含直线型裂隙试件的拉应力集中区分布于裂隙端部周边。从图9（b）中可以看出，含折线型裂隙试件的应力分布不同于含直线型裂隙试件，拉应力集中于裂隙折角处。最大主应力最大值所处的位置就是裂纹起裂处，有限元计算结果表明预制裂隙几何形态会影响应力场分布，进而使得裂纹起裂位置发生改变。

图8 起裂应力与最大主应力最大值Fig.8 Crack initiation and maximum principal stress

图9 数值试件最大主应力云图Fig.9 Contours of the maximum principal stresses of the numerical specimens

2.2 裂纹扩展过程及其机制解释

图10 和图11 给出了同一轴向应变水平下含直线型和折线型裂隙试件的裂纹扩展。当加载至标记点BS和BF，这2 类试件的裂纹扩展路径均先弯曲，随后逐渐近似平行于轴向加载方向朝着试件上、下两端以稳定的方式扩展，裂纹扩展一定长度后即停止，如图10（a）和图11（a）所示。结合DIC 计算结果可知，应变局部化带和位移不连续也随着裂纹扩展而逐渐延伸，应变和位移明显大于裂纹起裂时的数值。从裂纹扩展路径周围的水平位移分布还可看出，2 类试件裂纹两侧的位移符号相反，处于相背运动状态，说明扩展过程中的裂纹依然处于受拉状态，见图10（d）和图11（d）。

图10 含直线型裂隙试件裂纹扩展及变形场（标记点BS）Fig.10 Crack propagation and deformation fields of the specimen containing a straight fissure (Point BS)

图11 含折线型裂隙试件裂纹扩展及变形场（标记点BF）Fig.11 Crack initiation and deformation fields of the specimen containing a folded fissure (Point BF)

图12 和图13 分别为扩展有限元法模拟的含直线型和折线型裂隙试件裂纹扩展过程及其最大主应力云图，与试验结果大体一致，见图6（a）、图7（a）、图10（a）、图11（a），这说明扩展有限元法能够实现裂纹扩展过程的数值再现。从图中还可以看出，拉应力集中区始终出现在新生裂纹尖端，这是引起裂纹起裂、扩展的驱动力。对比图12（a）（b）和图13（a）（b）可知，裂纹尖端的最大主应力最大值逐渐变小，这是因为在裂纹扩展过程中拉应力逐渐释放，直到裂纹尖端的拉应力小于岩石抗拉强度，翼型裂纹便停止扩展，这从应力场的角度证明了翼型裂纹以稳定的方式扩展。

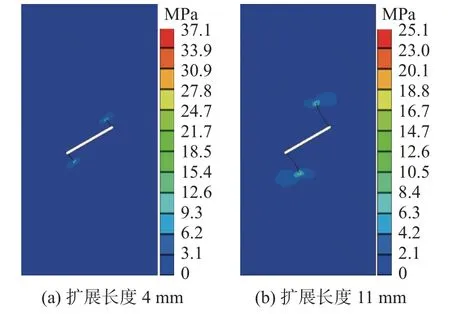
图12 含直线型裂隙试件裂纹扩展数值模拟Fig.12 Numerical simulation of crack propagation for the specimen containing a straight fissure

图13 含折线型裂隙试件裂纹扩展数值模拟Fig.13 Numerical simulation of crack propagation for the specimen containing a folded fissure

2.3 破坏模式

含直线型和折线型裂隙试件最终发生对角剪切破坏，如图14所示，分别对应于应力-应变曲线中的标记点CS和CF，这说明裂隙几何形态并未改变试件最终破坏模式。裂隙左、右尖端周围出现剪切裂纹(记为S)，分别沿着试件的左下角和右上角迅速扩展，形成贯通破裂面，导致试件发生失稳破坏。

图14 含裂隙砂岩试件最终破坏模式Fig.14 Ultimate failure mode of the sandstone specimens containing a fissure

3 讨论

为分析不同裂隙起伏度的影响效应，本次研究还制备了起伏度β= 10°和β = 30°的含折线型裂隙砂岩试件。物理试验和数值模拟所得的裂纹扩展路径如图15、图16所示，再次说明扩展有限元方法在模拟岩石裂纹扩展问题的有效性。从图中还可以发现，裂纹均未在预制裂隙尖端处起裂，与起伏度β= 20°的试件结果一致，进一步说明裂隙起伏形态会影响岩石裂纹起裂与扩展行为。

图15 起伏度10°时的含折线型裂隙砂岩试件裂纹扩展Fig.15 Crack propagation for the specimen containing a folded fissure with β = 10°

图16 起伏度30°时的含折线型裂隙砂岩试件裂纹扩展Fig.16 Crack propagation for the specimen containing a folded fissure with β = 30°

4 结论

（1）通过数字图像相关方法追踪应变局部化带演化，成功识别出新生裂纹的扩展路径。位移场计算结果进一步表明，在试件加载过程中，翼型裂纹两侧的岩石发生相背运动，或者发生相向运动，但是一侧位移量大于另一侧，即都呈张开状态。

（2）含直线型和折线型裂隙试件的裂纹萌生位置不同，前者萌生于预制裂隙尖端，而后者则出现在预制裂隙折角处，这是因为裂隙几何形态会显著影响试件应力场分布。有限元数值计算结果表明，含直线型和折线型裂隙试件的最大拉应力集中区域分别分布于预制裂隙尖端和折角处，这是裂纹萌生的发源点，解释了裂纹起裂位置与裂隙几何形态之间的相关性。

（3）含折线型裂隙试件的起裂应力小于含直线型裂隙试件，这是也与应力分布特征密切相关。有限元数值计算结果表明，相同加载条件下含折线型裂隙试件的最大拉应力大于含直线型裂隙试件，即折线型裂隙周围更容易产生裂纹。

（4）含直线型和含折线型裂隙试件的翼型裂纹分别沿着垂直于预制裂隙方向和裂隙折角角平分线方向扩展，逐渐发生弯曲，最后均近似沿着轴向加载方向延伸。扩展有限元能够数值再现这一断裂过程，计算所得的裂纹扩展路径与试验结果大体一致，裂纹尖端集中的拉应力是驱动裂纹扩展的动力。宏观剪切裂纹最终贯穿这2 类试件，导致试件失稳破坏，说明裂隙几何形态未改变最终破坏模式。

需要指出的是，本文着重研究了含30°裂隙倾角、20°起伏度的折线型裂隙砂岩翼型裂纹起裂与扩展。下一步将设计更多的裂隙倾角和起伏度组合，增加更多的相同试件数量，并开展三维裂纹扩展模拟，以使研究结论更具普适性。