基于伪地震数据模式学习的多次波自适应相减方法

姜博午,刘金朋,陆文凯

(1.北京化工大学机电工程学院,北京100029;2.智能技术与系统国家重点实验室,北京 100084;3.北京信息科学与技术国家研究中心,北京 100084;4.清华大学自动化系,北京 100084;5.中海油田服务股份有限公司物探事业部特普公司,广东湛江524057)

工业界常用的基于伴随算子的地震偏移成像算法假设地震数据中只存在一次反射波(一次波),而多次反射波(多次波)的存在不符合传统成像算法的假设条件,造成有效波振幅、频率、相位畸变,影响地震解释[1]。多次波广泛存在于陆地和海洋地震数据中,特别是在海洋地震数据中,由于存在海面和海底两个强反射界面,因而导致海洋地震数据的表面多次波干扰问题更为严重。对于陆上地震数据而言,当地下存在强反射界面,诸如基岩面、火成岩侵入体、不整合面等,地震波在强反射界面间或其内部发生多次反射,形成层间多次波[2]。由于多次波传播路径更加复杂,因而压制层间多次波更有挑战性。多次波压制方法主要分为两类:滤波法和预测相减法[3]。滤波类方法利用一次波和多次波在变换域内的差异压制多次波,包括F-K滤波[4]、Radon变换滤波方法[5-8]等。通常当一次波和多次波速度差异较大时,滤波类方法效果较理想;但当地下介质复杂时,滤波类方法很难在保护有效信号的同时压制多次波。预测相减法首先基于波动理论得到预测多次波模型,然后通过自适应相减压制多次波。这类算法更加适用于复杂介质情况。BERKHOUT等[9]与VERSCHUUR等[10]基于反馈迭代模型,提出了表面多次波去除方法(SRME),该方法已经成为工业上成熟应用的表面多次波去除方法。针对层间多次波的复杂波场特征,诸多国内外地球物理研究人员发展了相应的层间多次波压制方法,包括逆散射级数法[7,11-13]、共聚焦点技术[14-15]和Marchenko层间多次波压制技术[16-17]等。

但是,在实际地震数据采集过程中,观测系统往往存在缺陷,震源子波常常不一致等。这些因素使得预测多次波模型往往存在相位、频带、振幅的差异[9]。因此,自适应相减方法作为预测相减法不可或缺的关键步骤,能够校正预测多次波模型中的误差。工业界最常用的基于最小二乘匹配滤波器的多次波自适应相减方法[10]利用预测多次波直接匹配观测数据,以去除多次波后的数据的L2范数最小为优化目标。该方法效率很高,可以快速估计出观测数据中的多次波。但是其仅在一次波和多次波正交假设下,才能取得较好的效果。随后,基于L1范数的匹配滤波器方法被提出[18]。该方法可以更好地处理一次波和多次波不正交的数据。独立成分分析方法也被应用于多次波自适应相减问题[19-20]。

基于模式学习的多次波自适应相减方法相继被提出[21-24]。模式学习方法首先从预测多次波中学习多次波特征,然后利用学习到的多次波特征去重构原始数据,这样就可以得到原始数据中的多次波,进而将其从原始数据中减去即可得到一次波数据。模式学习方法将多次波衰减分为多次波模式学习和自适应相减两个独立过程,能够更好地保护有效信号。本文基于混合L2-L1范数模式学习方法[24],衰减地震数据中的多次波。同时,针对预测多次波模型中存在的相位和频带误差,引入伪地震数据[25-28],在不损伤有效信号的同时,进一步减少多次波残留。最后利用模拟数据和实际数据验证本文方法的有效性。

1 技术方法

1.1 混合L2-L1范数模式学习方法

采用SRME预测多次波模型m∈h×w,其中,w表示地震道数,h表示地震道采样点数。我们利用主成分分析(Principle Component Analysis,PCA)方法来提取预测多次波的关键模式。首先将预测多次波模型m划分为n个互相重叠的大小为d=k×l的图像块,再将这些图像块向量化之后合成一个矩阵M∈d×n,其中,n=(h-k+1)×(w-l+1)。对该矩阵进行PCA特征编码,有:

(1)

式中:B∈d×p表示学习到的p个d维特征向量构成的特征矩阵;X∈p×n表示对应的特征系数。特征矩阵B的构建过程如下。

算法1:SVD求解公式。

1)初始化:通常λ=0.1。

2)对数据矩阵M作SVD分解,有[U,Σ,V]=SVD(M)。

3)设Σ=diag({σi}1≤i≤N),选择前p个最大的特征值,使得σp+1<λσ1,且σp≥λσ1。

4)设U=[u1,u2,…,un],选择前p个最大的特征值对应的特征向量,构成特征矩阵B=[u1,u2,…,up]。

考虑分频编码策略,用带通滤波器将预测多次波模型分为低、中、高3个不同的频段,即mLF,mMF,mHF。相应的低、中、高频数据矩阵记为MLF,MMF,MHF。利用算法1学习分频段特征矩阵BLF,BMF,BHF。

最终的分频特征矩阵为:

B=[BLF,BMF,BHF]

(2)

由此,我们可以得到预测多次波m的特征矩阵B[24]。在完成模式学习并学习到多次波的特征之后,我们便可以利用学习到的特征去重构观测数据中包含的多次波,进而分离出观测数据的一次波,即自适应相减过程。本质上是估计一组系数,使得多次波关键模式线性组合后,与观测数据的差异最小。

与模式学习过程相对应,我们将观测数据s(包含多次波和一次波)划分为若干个大小为k×l的重叠图像块,再将这些图像块向量化之后组合成一个矩阵S∈d×n。在数据矩阵S中,每个列向量对应一个原数据s中的图像块。我们用L1范数来重构多次波[24]:

(3)

令P=S-BY即一次波数据矩阵,其中P∈d×n,公式重写为:

(4)

由拉格朗日乘数法,引入一个罚函数,我们将公式(4)转化为一个无约束的优化问题:

(5)

其中,μ为惩罚系数,且μ>0。当μ较小时,公式(5)求解不准确;当μ较大时,公式(5)求解数值不稳定。为避免μ调参复杂,我们利用裂步Bregman算法[29]求解公式(5)。引入中间变量Ak,且A1=0,则:

(6)

Ak+1=Ak+S-BYk+1-Pk+1

(7)

在裂步Bregman算法[29]中,公式(7)用来添加约束,避免选择一个较大的μ带来的数值不稳定问题。通常,我们选择μ=1。公式(6)两个变量P和Y是解耦的,我们可以利用交替下降法近似求解公式(6):

(8)

(9)

公式(8)和公式(9)的解析解为:

Yk+1=(BTB)-1BT(S+Ak-Pk)

(10)

(11)

裂步Bregman算法[29]求解自适应相减问题(公式(3))的步骤总结如下。

算法2:裂步Bregman算法[29]求解公式。

1)初始化:k=1,A1=0,P1=0,P0=S,D=(BTB)-1。

2)While‖Pk-Pk-1‖2>γdo。

3)Yk+1=DBT(S+Ak-Pk)。

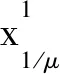
5)Ak+1=Ak+(S-BYk+1-Pk+1)。

6)k=k+1。

7)End while。

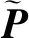
1.2 基于伪地震数据的模式学习

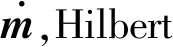
(12)

在得到特征矩阵B后,利用算法2重构观测数据中的多次波,进而分离一次波和多次波。图1展示了基于伪地震数据的多次波模式学习和自适应相减方法流程。

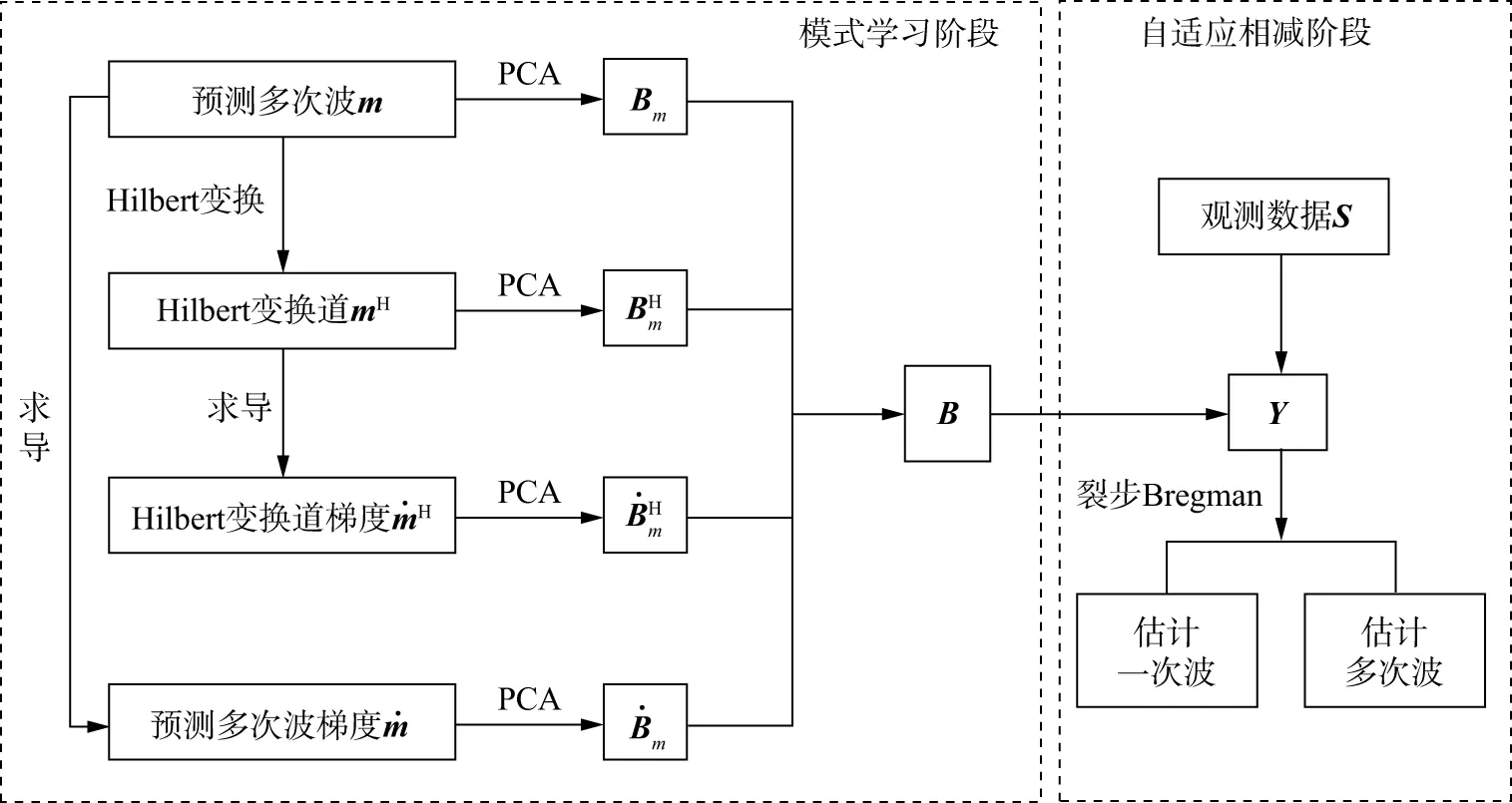
图1 基于伪地震数据的多次波模式学习和自适应相减方法流程

2 应用实例

2.1 Sigsbee模拟数据

采用Sigsbee模拟数据验证算法的有效性[23]。图2a,图2b和图2c分别展示了真实一次波、预测多次波模型和观测数据。我们对真实多次波进行如下处理生成预测多次波模型:纵向错动3个网格,横向错动2个网格,然后与主频20Hz,长30个单位网格的雷克子波进行褶积。图3a,图3b和图3c分别展示了采用分频模式学习方法估计的一次波、多次波和误差。图4a,图4b和图4c分别展示了采用伪地震数据模式学习方法估计的一次波、多次波和误差。对比图3c 和图4c可以发现,伪地震数据模式学习方法误差更小,在未损伤一次波的基础上,多次波残留更少。定量来看,分频模式学习方法和伪地震数据模式学习方法估计的一次波信噪比分别为19.03dB和20.06dB,伪地震数据模式学习方法的信噪比提升了1dB。图2中箭头所指位置强能量多次波造成分频模式学习方法存在多次波残留,而伪地震数据模式学习方法明显残留更少。为了更清晰地对比,我们将图2 至图4中红色框部分放大显示(图5至图7)。由于绕射多次波预测不准,分频模式学习方法残留绕射多次波严重。伪地震数据模式学习方法几乎完全压制了绕射多次波。因此,相比于分频模式学习方法,伪地震数据模式学习方法在不损伤一次波的基础上,能够有效避免多次波残留,特别是对绕射多次波压制效果更佳。

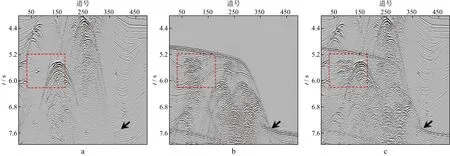
图2 Sigsbee模拟数据a 真实一次波;b 预测多次波;c 观测数据

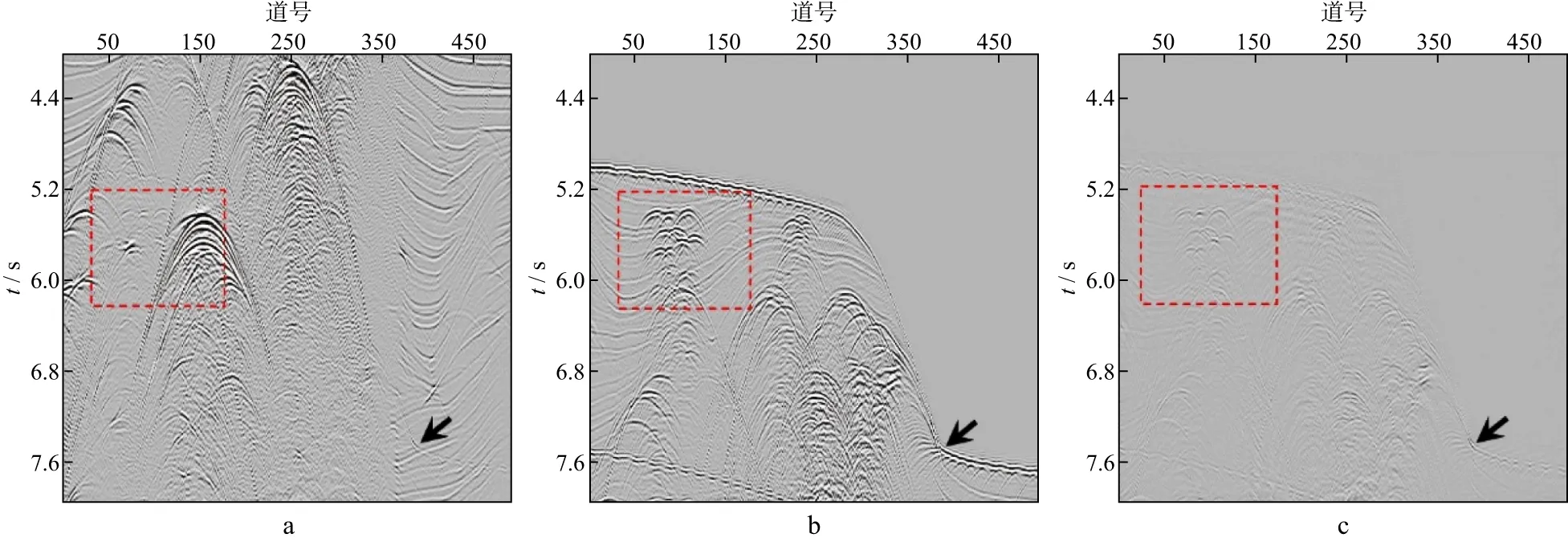
图3 采用分频模式学习方法估计的一次波(a)、多次波(b)和误差(c)

图4 采用伪地震数据模式学习方法估计的一次波(a)、多次波(b)和误差(c)

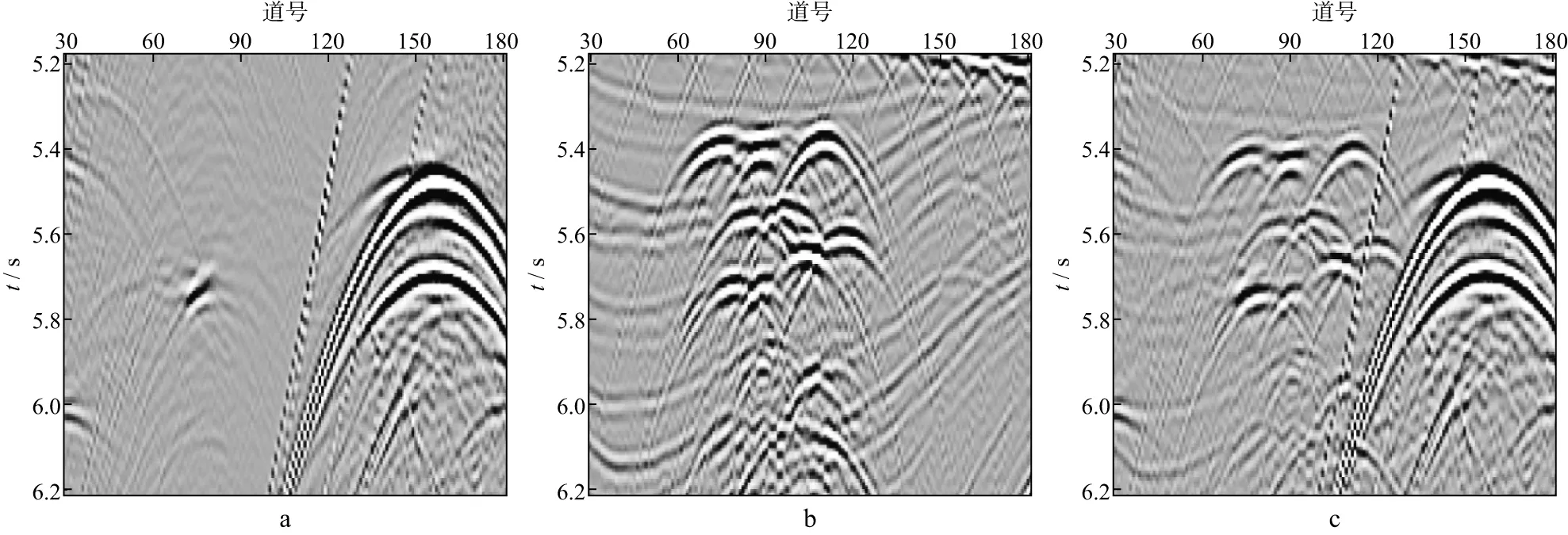
图5 图2红色框位置的放大显示结果a 真实一次波;b 预测多次波;c 观测数据

图6 图3红色框位置的放大显示结果a 分频模式学习估计的一次波;b 分频模式学习估计的多次波;c 分频模式学习的误差

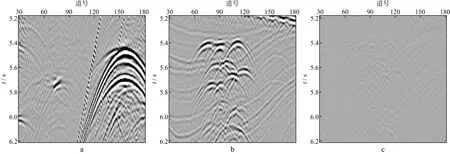
图7 图4红色框位置的放大显示结果a 伪地震数据模式学习估计的一次波;b 伪地震数据模式学习估计的多次波;c 伪地震数据模式学习的误差

2.2 海上实际数据

我们对海上实际地震资料进行了多次波压制。图8a和图8b分别显示了观测数据和预测多次波模型;图9a和图9b分别显示了采用分频模式学习方法估计的一次波和多次波;图10a和图10b分别显示了采用伪地震数据模式学习方法估计的一次波和多次波。对比图8 至图10中箭头所指处可以看出,强能量多次波导致分频模式学习方法存在一个低频残留;而伪地震数据模式学习方法不存在这一问题。放大显示图8至图10中的矩形框1和矩形框2,如图11至图16所示。图11至图13中箭头所指位置尖灭构造生成复杂多次波。由于多次波预测过程中多次褶积的影响,存在相位误差。分频模式学习方法存在一个明显和多次波走势相同的残留。伪地震数据模式学习方法减少了多次波残留。图14至图16中箭头所指位置绕射多次波发育。但由于大角度绕射多次波预测误差较大,导致分频模式学习方法并没有很好地压制掉大角度的绕射多次波,而伪地震数据模式学习方法能够缓解这一问题。但是对于更大角度处,预测多次波时移误差更大,仍然存在部分残留。

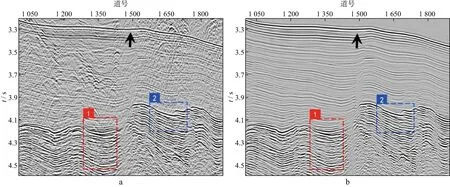
图8 海上实际地震资料a 观测数据;b 预测多次波

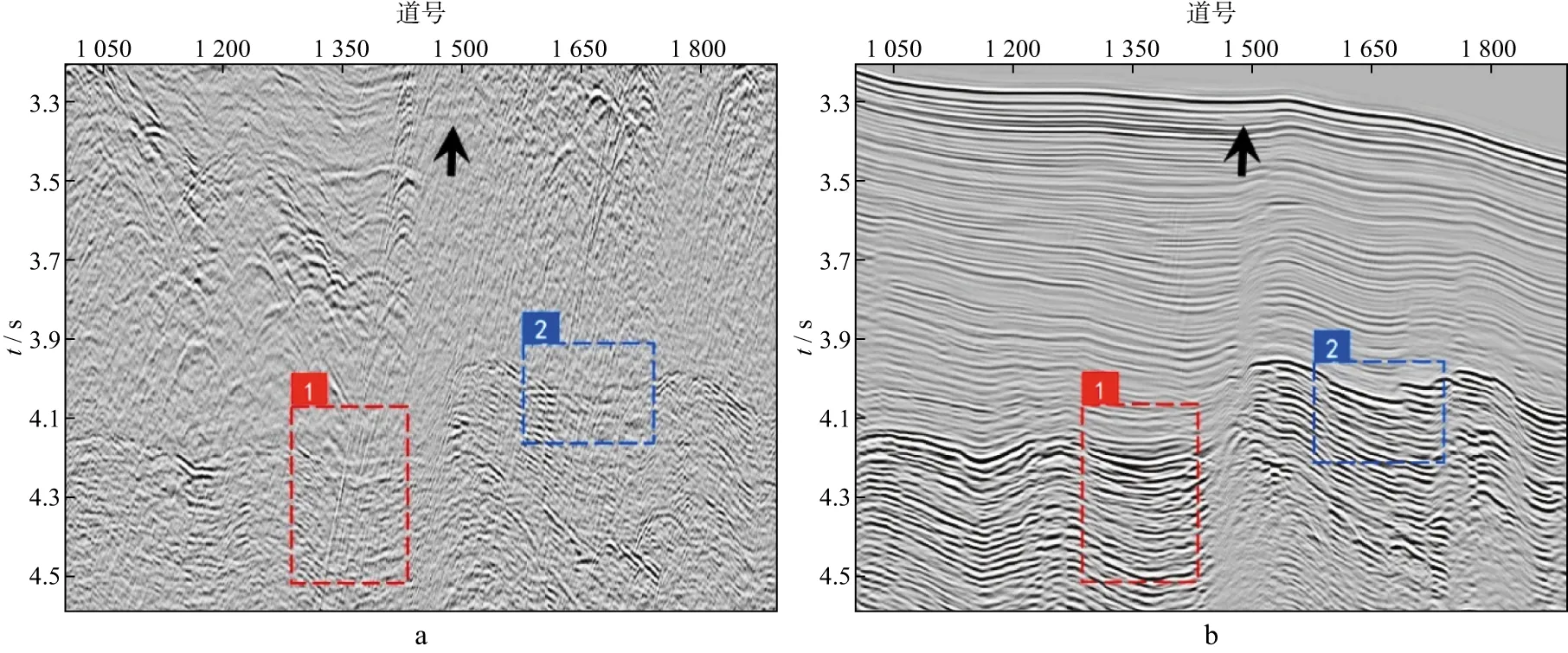
图9 采用分频模式学习方法估计的一次波(a)和多次波(b)

图10 采用伪地震数据模式学习方法估计的一次波(a)和多次波(b)

图11 图8中矩形框1的放大显示a 观测数据;b 预测多次波

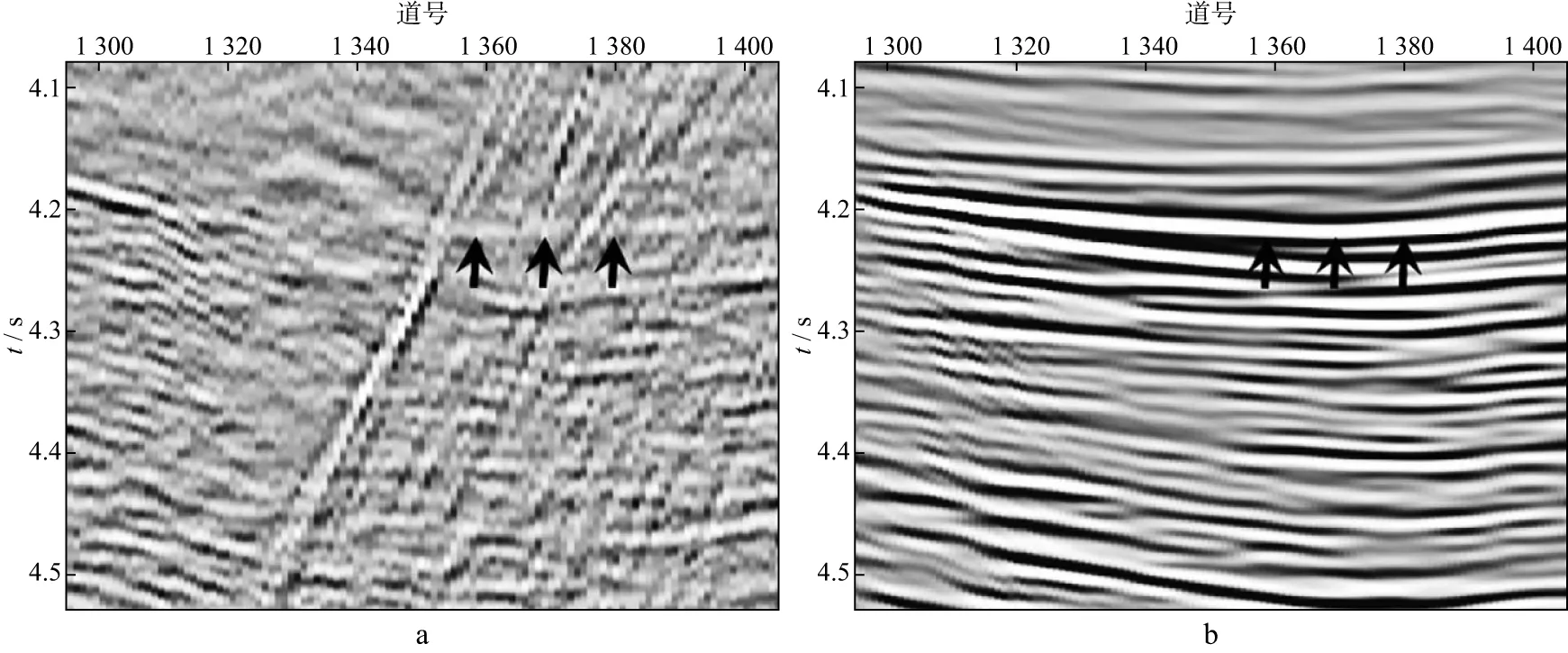
图12 图9中矩形框1的放大显示a 分频模式学习估计的一次波;b 分频模式学习估计的多次波

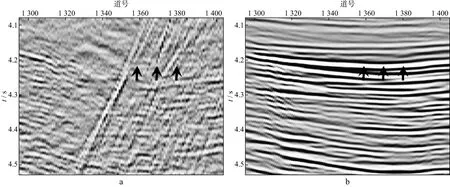
图13 图10中矩形框1的放大显示a 伪地震数据模式学习估计的一次波;b 伪地震数据模式学习估计的多次波

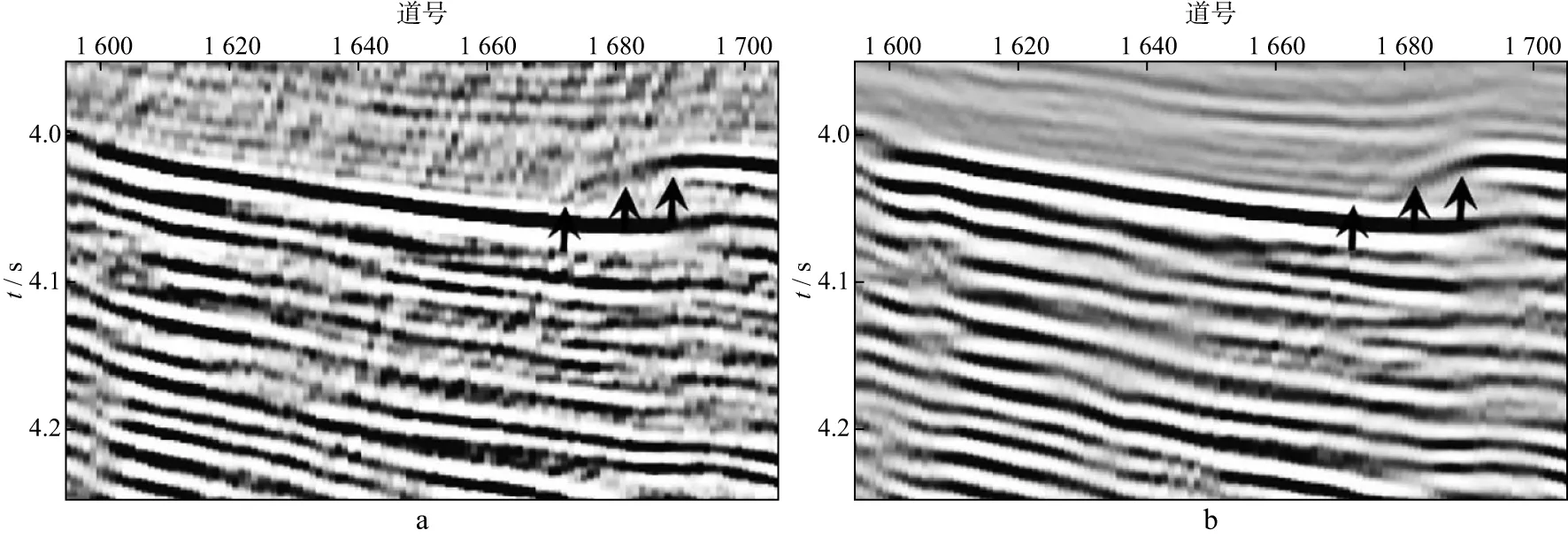
图14 图8中矩形框2的放大显示结果a 观测数据;b 预测多次波

图15 图9中矩形框2的放大显示结果a 分频模式学习估计的一次波;b 分频模式学习估计的多次波

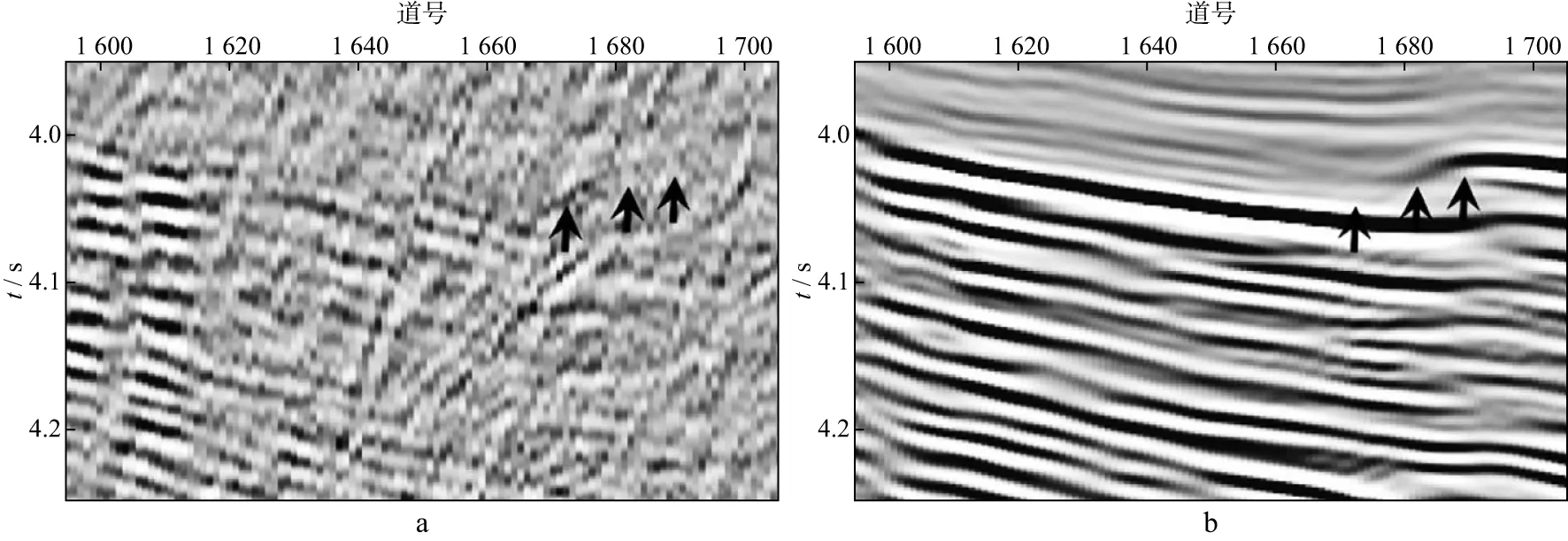
图16 图10中矩形框2的放大显示结果a 伪地震数据模式学习估计的一次波;b 伪地震数据模式学习估计的多次波

3 结论

本文提出了一种基于伪地震数据的多次波模式学习和自适应相减方法。该方法一方面能够继承模式学习方法的优势,更好地保护有效信号;另一方面,利用了伪地震数据中额外的相位和高频信息,避免了多次波残留。Sigsbee模拟数据实验结果表明,相比于分频模式学习方法,本文提出的伪地震数据模式学习方法一次波信噪比能够提升1dB。海上实际数据应用结果表明,分频模式学习方法在多次波复杂情况下效果不佳,本文方法能够更好地消除大角度的绕射多次波。但是当绕射多次波预测时移误差更大时,仍然存在一定残留。事实上,可以通过进一步调参来消除更大时移误差,但会损伤部分有效信号。因此,对于实际地震数据,多次波预测误差变化较大时,必须要在保护一次波和压制多次波之间进行折衷处理。