地震岩石物理驱动的裂缝预测技术研究现状与进展(Ⅱ)——五维地震裂缝预测技术

印兴耀,马正乾,宗兆云,商 硕

(1.中国石油大学(华东)地球科学与技术学院,山东青岛266580;2.海洋国家实验室海洋矿产资源评价与探测技术功能实验室,山东青岛266071)

正如“地震岩石物理驱动的裂缝预测技术研究现状与进展(Ⅰ)”的引言所述,地震预测技术的探测深度大、范围广等特征是地质、岩心和测井技术等非地震手段所不具备的,而且地震P波振幅[1]、阻抗[2-4]、衰减[5-6]等属性随入射角和方位角变化(五维地震)技术较其它地震裂缝预测技术具有更高的分辨率和抗噪性,可获得更多的储层信息且纵波数据易获得。所以在第(Ⅰ)部分[7]综述了裂缝储层等效各向异性岩石物理理论研究现状与进展的基础上,第二部分(Ⅱ)主要阐述地震P波属性随入射角和方位角变化(五维地震)的裂缝预测技术研究现状与进展。

五维地震数据较常规叠后数据增加了方位和偏移距维度,蕴含着更加丰富的储层裂缝等各向异性信息[8-9],所以基于五维地震数据的裂缝信息解耦与提取得到了越来越多的关注[10-14]。根据裂缝指示因子的差异,目前基于五维地震数据的裂缝预测技术可大致分为基于椭圆分析的裂缝预测方法和基于岩石物理理论的裂缝参数反演方法,前者利用拟合椭圆参数指示裂缝分布,后者利用反演得到的岩石物理参数及其组合实现裂缝参数的空间描述。所以我们将从两方面阐述基于五维地震数据随方位角和入射角变化的裂缝预测理论与方法的研究现状。

1 基于椭圆分析的裂缝预测方法

基于椭圆分析裂缝预测方法的科学实质是裂缝介质诱导的地球物理响应在方位角域呈周期性变化,且这种变化的极值点与裂缝对称轴构成映射关系。目前研究中,可用于椭圆分析的参数主要包括运动学参数和动力学参数,运动学参数包括动校正速度[15-17]和各向异性剩余时差[18-19]等,动力学参数包括AVO梯度和杨氏模量等。前者主要利用地层裂缝诱导的地震波旅行时方位差异实现裂缝参数预测,目前在HTI型[17-19],OA(orthorhombic medium)型[15]、TOA(titled orthorhombic medium)型[16,20]裂缝储层中均有研究和应用;后者的理论基础是地震波振幅的方位差异,目前主要应用于HTI型裂缝储层。所以我们将以各向同性背景中包含一组垂直平行裂缝介质(parallel vertical fractures in isotropic background,VFI)为例,详细介绍基于AVO梯度椭圆拟合[21]和方位杨氏模量椭圆拟合[22]的裂缝预测技术。

1.1 基于AVO梯度椭圆拟合的裂缝预测方法

RÜGER[23]给出了HTI介质反射系数近似公式,可将其简写为:

(1)

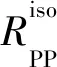
(2)

根据公式(2),可逐方位对五维地震数据进行AVO分析[24],将估计的多方位AVO梯度进行椭圆拟合[25],拟合椭圆的主轴指示裂缝对称轴方位(后文简称裂缝方位),椭圆率指示裂缝密度分布特征。但逐方位AVO分析获得的自激自收反射系数P很难保证相等,影响AVO梯度G(φ)的提取精度,所以可联合五维地震数据构建反演方程,以保证自激自收反射系数P在方位角域的常值特征[26]。此外,如图1所示,对于不同模型参数(表1),裂缝走向和裂缝对称轴方向的AVO梯度相对大小不同,即AVO梯度拟合椭圆的长轴对应裂缝走向还是裂缝对称轴方向不明确,通常将此现象称为90°模糊性。导致90°模糊性的根本原因为AVO梯度可表达为G(φ)=A+Bcos[2(φ-φsym)],呈现周期为π的余弦变化规律,式中:A,B均为介质弹性参数和各向异性参数的函数;φsym为裂缝对称轴。当参数B为正数时,裂缝对称轴方向的AVO梯度取最大值,即G(φsym)=A+|B|;当参数B为负值时,裂缝对称轴方向的AVO梯度取最小值,即G(φsym)=A-|B|。由于B可为正数,也可为负数,取决于岩石弹性参数和各向异性参数,而且周期为π的余弦曲线最大函数值和最小函数值的相位差为90°,所以在岩石性质未知的情况下,利用AVO梯度椭圆拟合的裂缝方位预测值存在90°模糊性,需要在先验方位约束下开展裂缝方位预测。图2是利用所述方法在A工区目的层裂缝参数预测结果,与测井解释结果相符,说明了方法的合理性。

表1 3层模型参数

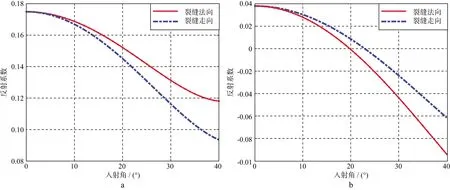
图1 表1所示模型的反射系数随入射角变化规律a 上界面;b 下界面

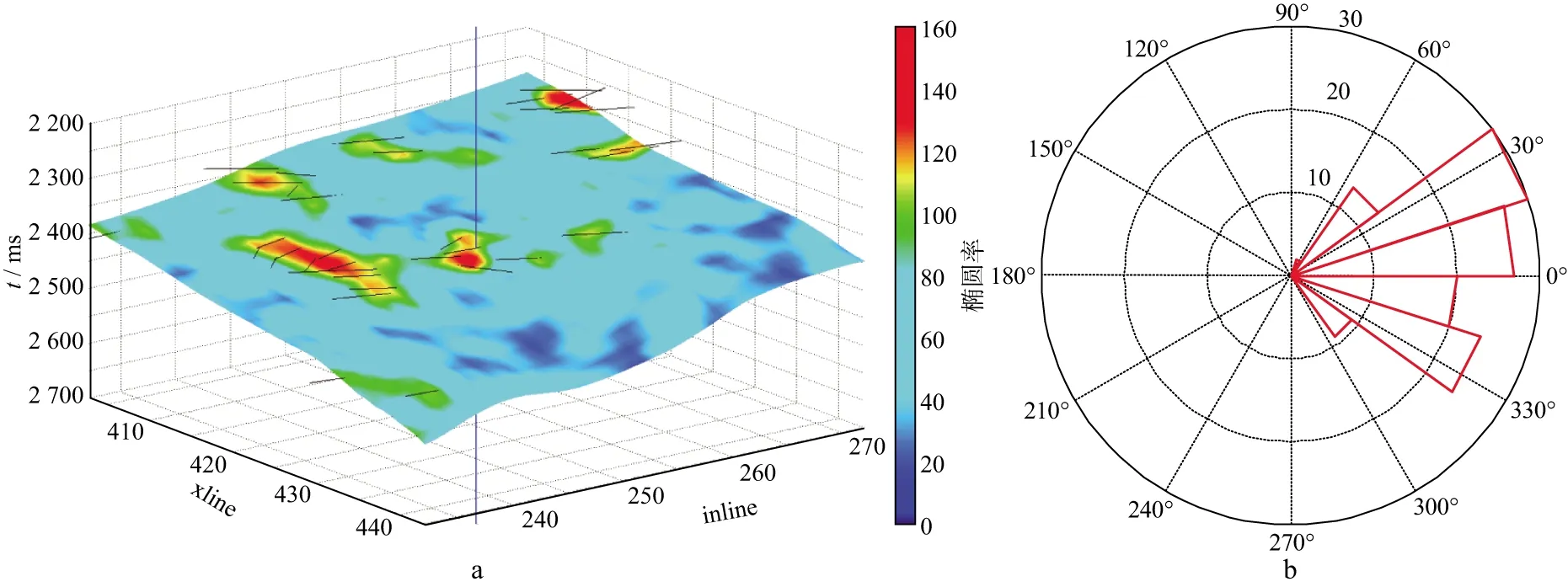
图2 基于AVO梯度椭圆拟合的A工区目的层裂缝预测结果a 裂缝密度(黑线代表裂缝走向);b 裂缝方位预测结果[26]

1.2 基于方位杨氏模量椭圆拟合的裂缝预测

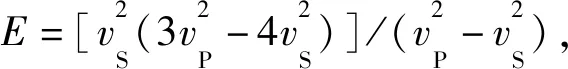
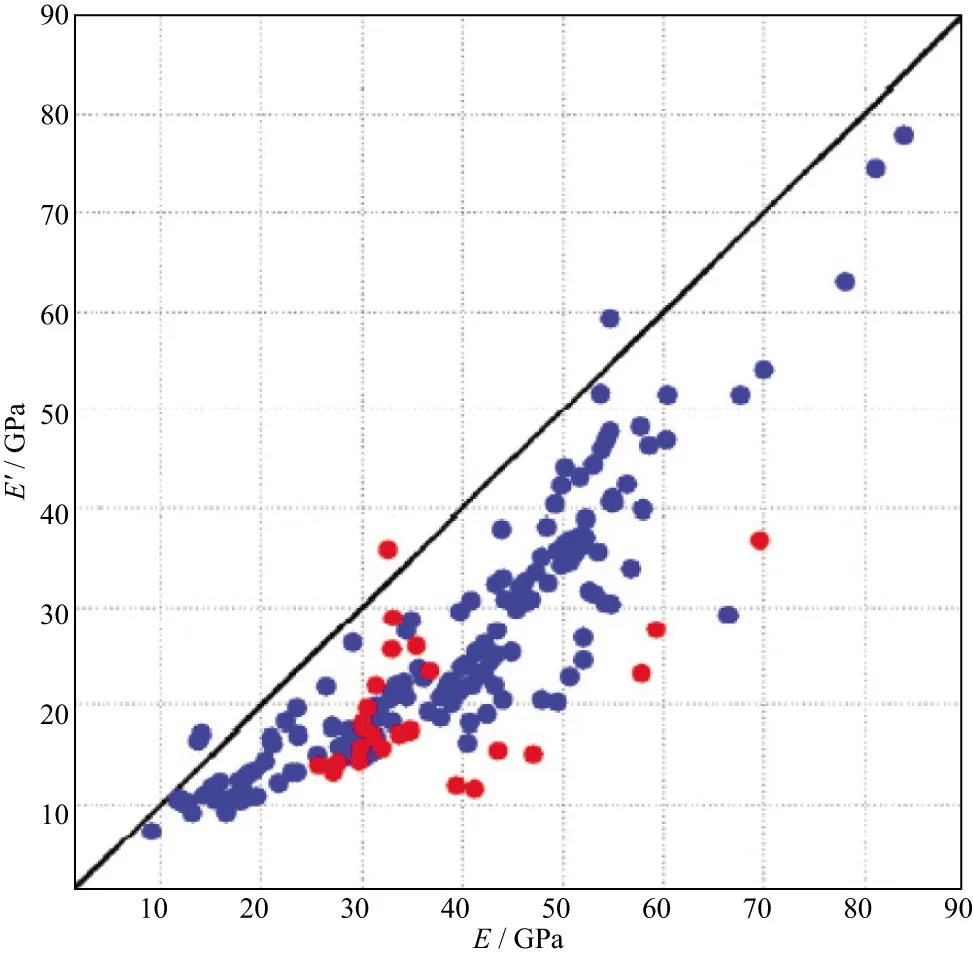
图3 VFI介质对称轴方向杨氏模量(Y轴)和对称面上杨氏模量(X轴)关系(红色代表静态测量结果,蓝色代表动态测量结果)

宗兆云等[28]推导了杨氏模量表示的反射系数方程和相应的弹性阻抗方程[29]:

(3a)

其中,

(3b)

(3c)

(3d)

式中:γ=β2/α2;α和β分别为纵、横波速度;EI为弹性阻抗;E、σ和ρ分别代表杨氏模量、泊松比和密度;下角标0代表归一化常数,一般为各弹性参数的平均值。基于公式(3),采用岩石物理驱动的阻尼最小二乘算法[30]或贝叶斯反演算法[31]等即可求得每个方位的杨氏模量,然后利用方位杨氏模量拟合椭圆参数实现储层裂缝预测。图4为基于方位杨氏模量椭圆拟合的A工区裂缝预测结果,与测井解释结果基本吻合。但和图2对比发现,基于AVO梯度与基于方位杨氏模量椭圆拟合的裂缝预测结果不完全相同,可能是由于两种方法的抗噪性不同和AVO梯度受子波影响较大等原因导致的。

图4 基于方位杨氏模量椭圆拟合的A工区裂缝预测结果a 椭圆率(指示裂缝密度);b 裂缝方位预测结果[26]

2 基于等效各向异性岩石物理理论的裂缝预测方法

地下储层物性特征复杂多变,根据储层空间的连通性,可分为孤立孔缝型储层、连通孔缝弹性储层及连通孔缝衰减型储层。针对不同类型储层,应采用不同的岩石物理模型进行表征(如前文[7]所述),即其模型参数化方法不一样。所以,本节将以等效各向异性岩石物理理论为基础,分别介绍这3种储层的模型参数化方法及裂缝参数预测的研究进展。

2.1 基于孤立孔缝岩石物理理论的裂缝预测方法

2.1.1 基于各向异性梯度的裂缝预测

在Schoenberg理论指导下,BAKULIN[32-33]指出各向异性梯度是很好的裂缝密度指示因子,为实现稳定的裂缝方位和各向异性梯度反演,李春鹏等[13]根据DOWNTON等[34]的分析,将公式(2)改写为:

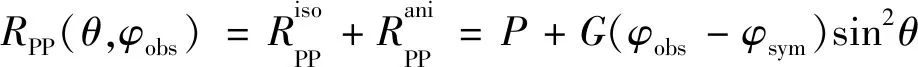
(4a)

其中,

(4b)

C=Ganicos2φsym

(4c)

D=Ganisin2φsym

(4d)

式中:Giso和Gani分别称为各向同性梯度和各向异性梯度。根据公式(4),在贝叶斯理论框架下,利用多方位地震数据便可实现P,B,C和D的反演[13]。然后,可估计各向异性梯度绝对值和裂缝方位,即:

(4e)

(4f)

从公式(4f)可发现,裂缝方位估计值存在90°模糊性,这是由于公式(4e)中的各向异性梯度符号难以确定而导致的,为此需要裂缝方位先验信息约束以消除90°模糊性。图5为该方法的模型测试结果。模型信噪比为4∶1,可以看出各向异性梯度分布能很好地预测裂缝密度分布,裂缝对称轴方位预测结果与模型也具有较高的吻合度。XIE等[17]又重新改写了公式(4a),利用最小二乘算法实现了裂缝方位和各向异性梯度的估计,但依旧存在90°模糊性问题。陈怀震等[35]基于弹性阻抗反演思想对该方法作了进一步发展,得到了更加稳定的结果。

图5 基于各向异性梯度的裂缝预测方法模型测试结果a 模型裂缝密度分布;b 模型裂缝方位玫瑰统计分析;c 各向异性梯度预测结果;d 裂缝对称轴方位预测结果玫瑰统计分析[26]

由于AVAZ反演(P-wave amplitude versus angle and azimuth inversion)的抗噪性比弹性阻抗反演低[36-37],所以基于公式(4)的裂缝参数直接反演很不稳定。曲寿利等[2-3]提出了阻抗随方位角变化(impedance versus azimuth,IPVA)的裂缝预测技术以提高稳定性。他们将阻抗写为观测方位角的余弦函数,即:

IP(φ)=AIP+BIPcos[2(φ-φsym)]

(5)

式中:IP(φ)为观测方位为φ的波阻抗,AIP和BIP为介质弹性参数和各向异性参数的函数,且BIP是裂缝密度的指示因子。在获得不同方位阻抗数据的基础上,利用公式(5)进行拟合,便可获得AIP,BIP和φsym的估计值,从而实现裂缝特征的刻画。季玉新等[4]将构造正反演裂缝预测技术与IPVA技术进行对比,发现二者预测结果基本吻合,进一步说明IPVA技术的有效性。但该技术依旧存在90°模糊性,而且裂缝诱导的各向异性比较弱,裂缝信息在阻抗数据中的比重较小,降低了裂缝参数预测的稳定性。为了弱化90°模糊性,进一步提高预测合理性,MA等[38-39]基于傅里叶级数展开,将裂缝方位先验信息作为约束条件,构建一个新的VFI介质方位弹性阻抗方程:

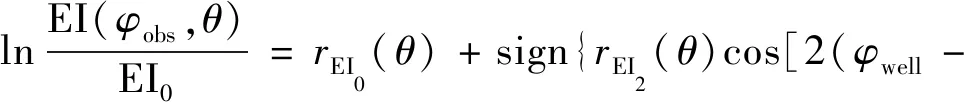
(6)

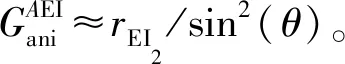
图6为B工区基于傅里叶级数的VFI介质裂缝参数预测结果。图6a为方位弹性阻抗各向异性梯度层位切片,黑线代表裂缝方位,预测结果与该地区的地质构造相契合。图6b为裂缝方位预测结果玫瑰统计,与图7所示的测井解释结果基本一致。MA等[41]基于傅里叶级数展开,也实现了VTI(vertically transverse isotropy)背景包含一组垂直定向裂缝诱导的OA介质(orthorhombic anisotropy)的裂缝参数预测,并取得较好的应用效果。

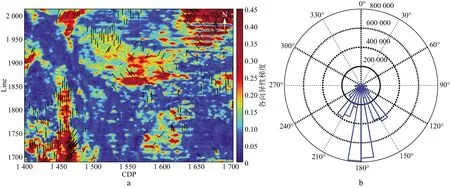
图6 B工区基于傅里叶级数的VFI介质裂缝参数预测结果a 方位弹性阻抗各向异性梯度层位切片(黑线代表裂缝对称轴方位);b 裂缝对称轴方位玫瑰统计分析[38]

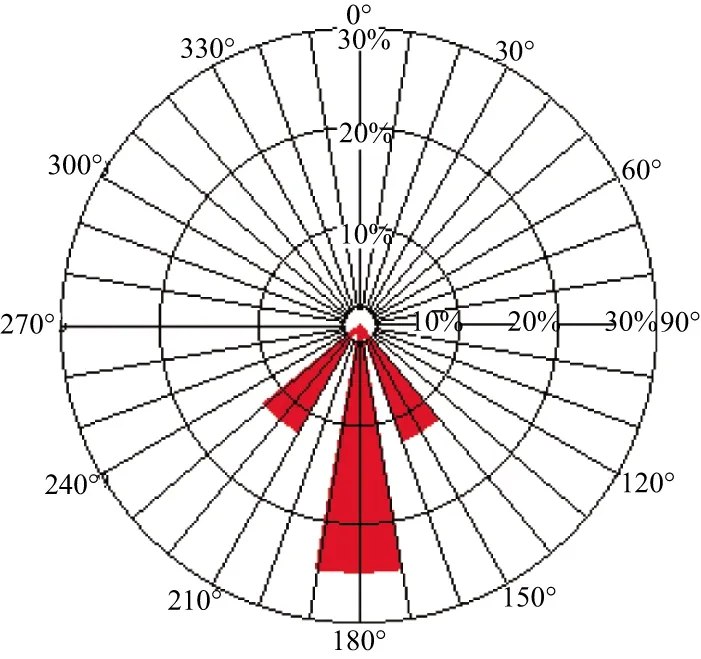
图7 B工区裂缝对称轴方位测井解释结果[38]

通过地震属性提取也可以直接获得各向异性梯度和裂缝对称轴方位[42]。以VFI介质为例,陈怀震[42]首先根据公式(4a)对3个观测方位φ1,φ2和φ3的地震数据进行AVO分析,提取截距P1,P2,P3和梯度属性G1,G2,G3,然后估计裂缝方位φsym,则有:

Dcos(2φ2)+Dcos(2φ1)]/[Dsin(2φ2)-

Dsin(2φ1)-sin(2φ3)+sin(2φ2)]}

(7a)

或

Dcos(2φ2)+Dcos(2φ1)]/[Dsin(2φ2)-

Dsin(2φ1)-sin(2φ3)+sin(2φ2)]}+90°

(7b)

其中,

(7c)

将估计值φsym带入Gani=(G3-G2)/[cos2(φ3-φsym)-cos2(φ2-φsym)]完成各向异性梯度Gani的估计。从公式(7)中发现,裂缝方位估计也存在90°模糊性[43],需要裂缝方位先验信息作为约束。MESDAG[44-45]指出,在多数情况下,各向异性梯度为正值,将其作为约束,也可弱化90°模糊性(注:文献[44]原文有误,后与作者讨论,确认大多数情况下各向异性梯度为正值)。对于OA型储层,也可采用相似的方法实现各向异性梯度和裂缝方位的估计[42]。但该方法提取的各向异性梯度属性分辨率较低,且抗噪性较差,只能作为勘探前期裂缝发育区的圈定手段,或为后期裂缝参数的稳定预测提供低频约束。

2.1.2 基于岩石物理参数的裂缝预测

1)各向同性背景中包含一组垂直定向裂缝(VFI)假设。从公式(6)可以看出,当孤立裂缝充填流体时,VFI介质裂缝切向弱度δT仅与裂缝密度有关,与裂缝充填流体类型无关,所以可利用切向弱度直接计算裂缝密度[32]:

(8)

印兴耀等[37,46-56]已经研究了多种流体识别方法,针对孤立定向裂缝介质,SCHOENBERG等[57]提出了一种有效识别裂缝流体类型的指示因子,即:

(9)

式中:ZN和ZT分别为裂缝法向和切向柔度参数。可以看出,裂缝密度e和流体指示因子ZN/ZT与裂缝弱度参数δN,δT和背景横、纵波速度比的平方γb有关,所以只要反演出裂缝弱度参数即可实现裂缝密度预测及流体识别。

CHEN等[30,58-59]将VFI介质反射系数方程舍去密度项后,改写为:

RPP(θ,φ)=sec2θRP-8γbsin2θRS-(γbcos2φ
sin2θ)(1-2γb)ΔδN+(γbcos2φsin2θ)ΔδT

(10)

(11)

公式(11)中的黑体变量代表与时间相关的函数,即地震道记录。在得到γb=(β/α)2=(IS/IP)2后,便可实现裂缝密度预测和流体识别。图8为C工区裂缝流体因子预测剖面,低值区代表饱含水层,高值区代表高含气层,中间值从小到大依次代表油水层和气水层。预测剖面很好地勾勒出含气区域的边界,与测井解释结果一致。陈怀震等[60-61]基于弹性阻抗反演思想对该方法作了进一步发展,以获得更加稳定的结果。

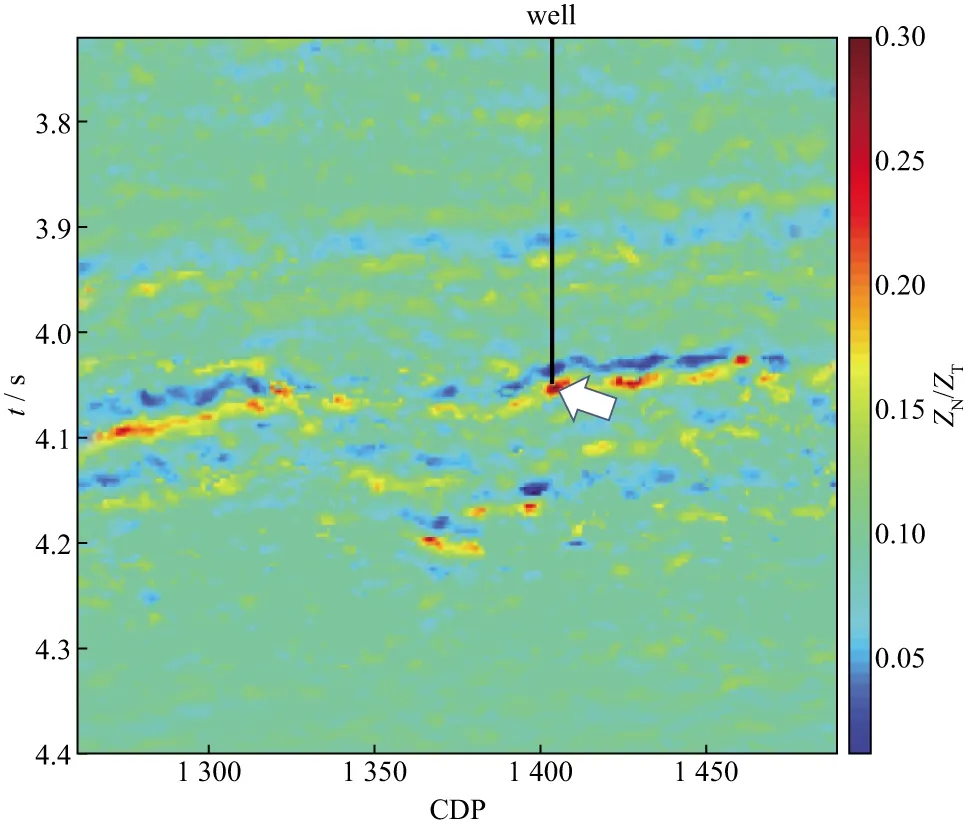
图8 C工区裂缝流体因子预测剖面[42]

VFI介质裂缝诱导的弱各向异性信息在地震数据中的比重远远小于各向同性信息,很容易被各向同性信息掩盖,所以CHEN等[62]根据SHAW等[63-64]提出的散射系数与反射系数的关系推导了VFI介质反射系数方程,即

(12)

根据振幅方位差异思想,得到不同观测方位反射系数差异表达:

ΔR(θ,φ)=[a(θ,φ2)-a(θ,φ1)]ΔδN+
[b(θ,φ2)-b(θ,φ1)]ΔδT

(13a)

其中,

(13b)

b(θ,φ)=-γb(sin2θtan2θsin2φcos2φ-sin2θcos2φ)

(13c)

公式(13)实现了裂缝各向异性信息与各向同性背景信息的解耦,可提高裂缝弱度参数预测稳定性。同时,法向弱度与切向弱度参数的相关性可能影响二者反演的稳定性,CHEN等[62]通过岩石物理分析,获得二者的线性关系δN=ξδT+Γ,代入公式(13),消除待反演参数的相关性,最后利用贝叶斯反演方法获得裂缝弱度参数,实现裂缝储层描述。PAN等[65]基于类似的思想,采用马尔科夫-蒙特卡洛反演算法(MCMC)进行裂缝储层描述。为了消除待反演参数的空间相关性,PAN等[66]也采用多尺度频率域反演方法,将地震数据变换到傅里叶频率域,再反演裂缝弱度参数。

LI等[67]将方位弹性阻抗方程写为傅里叶级数形式,即

LEI(φobs,θ)=a0(θ)+a2(θ)cos(2φobs)+b2(θ)·
sin(2φobs)+a4(θ)cos(4φobs)+b4(θ)sin(4φobs)

(14)

其中,

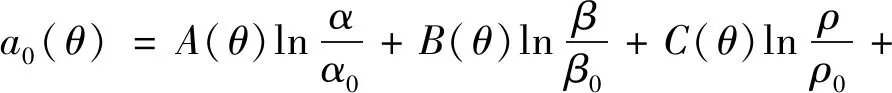
a2(θ)=H(θ)cos(2φsym)δN+I(θ)cos(2φsym)δT

b2(θ)=H(θ)sin(2φsym)δN+I(θ)sin(2φsym)δT

a4(θ)=J(θ)cos(4φsym)δN+K(θ)cos(4φsym)δT

b4(θ)=J(θ)sin(4φsym)δN+K(θ)sin(4φsym)δT

A(θ),B(θ),C(θ),F(θ),G(θ),H(θ),I(θ),J(θ)和K(θ)均是横、纵波速度比的平方γb和入射角θ的函数。公式(14)同样解耦了裂缝信息与背景信息,提高了裂缝弱度参数反演稳定性。此时,裂缝方位被估计为:

(15)

但仍存在90°模糊性。LI等[67]采用各向异性岩石物理建模方法减弱该效应。类比于方位弹性阻抗,MESDAG等[44]通过重组反射系数方程,提出等效弹性参数,并将其表达为傅里叶级数形式:

A′=b0+b1cos[2(φobs-φsym)]+b2cos
[4(φobs-φsym)]

(16)

式中:A′代表等效弹性参数;bi代表等效弹性参数第i阶傅里叶系数。对于不同弹性参数,bi具体表达不同。MESDAG等[45]分析发现,公式(16)中二阶傅里叶系数一般为正值,所以基于公式(16)可实现无90°模糊性的裂缝方位估计及裂缝密度预测。

以上方法通常要求方位分扇叠加数据,JENNER[68]指出,方位分扇叠加数据会造成:①丢失了部分方位信息;②即使某个方位扇具有较低的覆盖次数,即该方位扇叠加数据具有较低的信噪比,但反演时依旧认为每个方位扇具有相同的权重,③方位扇分析结果经常受到采集系统的影响。据此,JENNER改写Ruger反射系数方程为:

R(θ,φobs)=P+[W11cos2φobs+2W12cosφobs
sinφobs+W22sin2φobs]sin2θ

(17)

式中:Wij是裂缝弱度和方位的函数。基于不分扇的方位数据,采用最小二乘算法,估计参数Wij和截距P,各向异性梯度和裂缝方位依次可估计为:

2)各向同性背景中包含一组倾斜定向裂缝(TTI)假设。CHEN等[69]利用Bond变换研究了倾斜定向裂缝分布在各向同性基岩情况(图9)的刚度矩阵,然后利用逆散射理论,在小入射角和裂缝倾角大于70°的假设下,推导了反射系数方程,即:

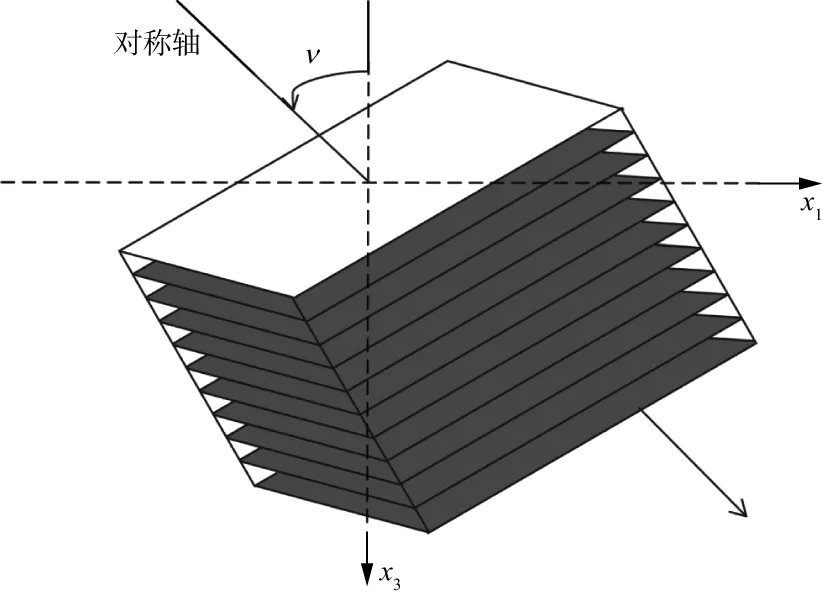
图9 裂缝诱导TTI模型[70]

γ(sin2θtan2θsin2φobscos2φobs+sin2θcos2φobs+

sin2θcos2φobs+cos2φobs)βT+

γ(sin2θsin4φobs-tan2θcos4φobs-cos2θ)δT

(18)

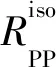
3)裂缝诱导的正交各向异性介质(OA)假设。裂缝诱导正交各向异性包括:①VTI背景包含一组垂直定向裂缝;②各向同性背景包含两组垂直定向旋转不变裂缝;③VTI背景包含两组垂直定向旋转不变裂缝;④各向同性背景包含一组水平旋转不变裂缝和一组垂直定向旋转不变裂缝等情况,如图10所示。

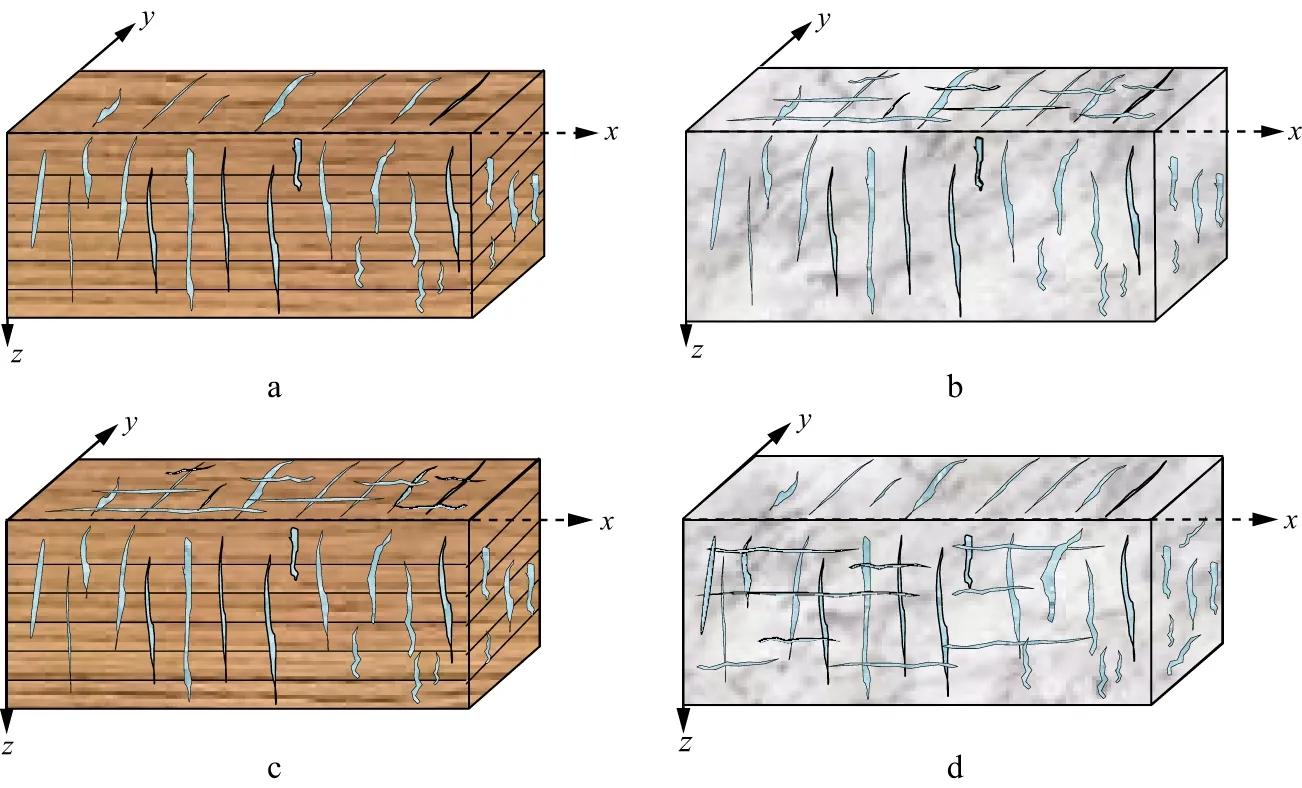
图10 裂缝诱导正交各向异性模型a VTI背景包含一组垂直定向裂缝;b 各向同性背景包含两组垂直定向旋转不变裂缝;c VTI背景包含两组垂直定向旋转不变裂缝;d 各向同性背景包含一组水平旋转不变裂缝和一组垂直定向旋转不变裂缝

针对情况①,CHEN等[71]采用逆散射理论可以获得反射系数方程,即

(19)

其中,

a(θ)=sec2θ,b(θ)=-8γbsin2θ
c(θ)=4γbsin2θ-tan2θ

e(θ)=sin2θtan2θ,f(θ)=sin2θ

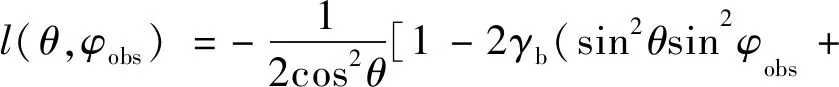
m(θ,φobs)=2γbsin2θcos2φobs

n(θ,φobs)=-2γbsin2θtan2θsin2φobscos2φobs

CHEN等[71]进一步推导了弹性阻抗方程,并基于方位地震数据,采用马尔科夫-蒙特卡洛反演算法实现了各向同性背景模量、背景各向异性参数和裂缝弱度参数的反演。PAN等[72]引入准弱度参数和相对各向异性参数来线性化方位弹性阻抗方程,提高参数反演稳定性。对于情况②和③,PAN等[11]利用散射理论分别推导了线性化反射系数方程。

对于情况④,ZHANG等[73]推导了线性化反射系数方程,并将其表达为傅里叶级数形式,即:

RPP(θ,φobs)=a0(θ)+a2(θ)cos(2φobs)+b2(θ)·
sin(2φobs)+a4(θ)cos(4φobs)+b4(θ)sin(4φobs)
=r0(θ)+r2(θ)cos{2[φobs-φsym]}+
r4(θ)cos{4[φobs-φsym]}

(20)

其中,加权振幅表示为:

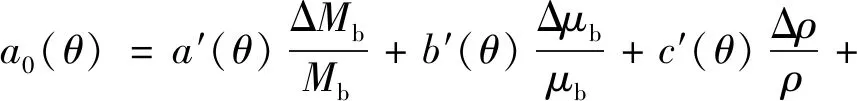
(21a)

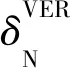
(21b)

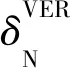
(21c)

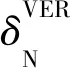
(21d)

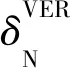
(21e)

2.2 基于连通孔缝低频岩石物理的裂缝预测方法

本节将从裂缝诱导VFI介质(一种HTI型介质)、TTI介质、OA介质三个角度分别阐述没有衰减特征或衰减特征不明显、孔缝连通储层的裂缝参数五维地震预测方法研究进展。

2.2.1 各向同性背景中包含一组垂直定向裂缝(VFI)假设

(22a)

(22b)

(22c)

(22d)

(22e)

(22f)

然后利用逆散射理论可推导流体体积模量表征的反射系数方程[77]:

(23)

其中,

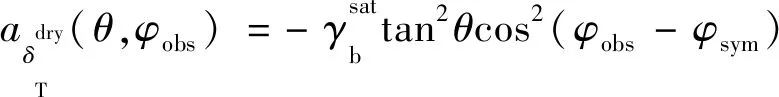
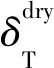
(24a)

(24b)

(24c)

(24d)

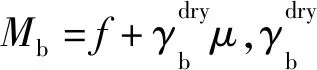
2.2.2 各向同性背景中包含一组倾斜定向裂缝(TTI)假设

对于TTI型裂缝储层,PAN等[70]仅考虑背景孔隙之间的流体流动,采用各向同性Gassman方程,将VFI介质的各向同性背景岩石模量写为Gassmann流体因子与干岩石骨架模量的和,然后利用Bond变换得到TTI介质刚度系数,即:

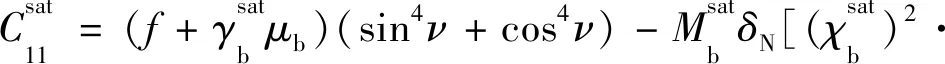
(25a)

(25b)

(25c)

(25d)

(25e)

(25f)

(25g)

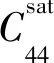
(25h)

(25i)

(25j)

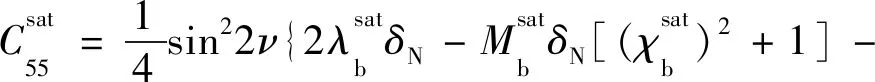
(25k)

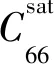
(25l)

然后推导出Gassmann流体因子f和裂缝弱度参数线性表征的反射系数方程和弹性阻抗方程,在获得裂缝倾角ν先验信息的前提下,实现TTI型裂缝储层流体分布和裂缝特征的线性化反演[70]。

2.2.3 裂缝诱导的正交各向异性介质(OA)假设

对于各向同性岩石中包含两组垂直正交定向裂缝系统的情况,可以假设每组定向裂缝系统诱导的各向异性比较微弱,则岩石整体的等效刚度系数可表达为等效流体体积模量和裂缝弱度参数的函数[79]:

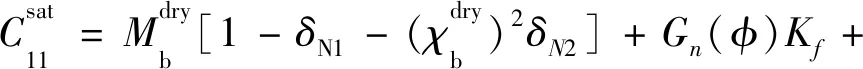
(26a)

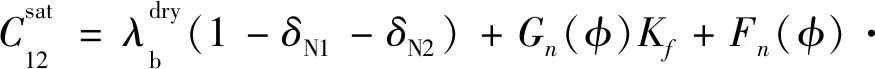
(26b)

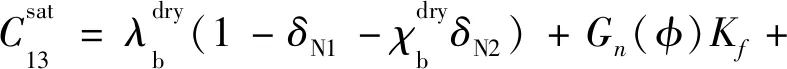
(26c)

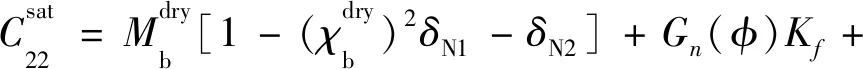
(26d)

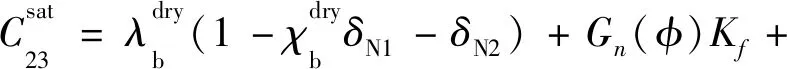
(26e)

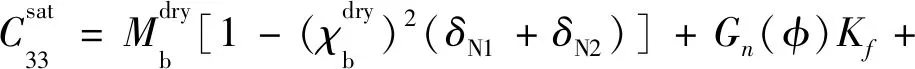
(26f)

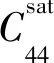
(26g)

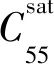
(26h)

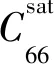
(26i)

(27)

式中:fm=φμb。基于公式(27),采用合理的反演算法便可实现裂缝储层定量表征。类似于TTI介质和VFI介质,对于各向同性背景包含两组垂直正交裂缝系统或VTI背景包含一组垂直裂缝系统诱导的OA介质,我们也可将背景各向同性部分的饱和岩石模量分解为Gassman流体因子与干岩石骨架部分,再推导Gassman流体因子与裂缝弱度参数表征的刚度矩阵和线性化反射系数方程[82],最后采用合理的反演算法实现裂缝储层表征和流体预测。

2.3 基于衰减岩石物理理论的裂缝预测方法

MAULTZSCH等[5,83]在研究Clair油田VSP资料时发现,沿裂缝法向和走向传播的地震波能量衰减值不一样,如图11所示。EKANEM等[84]和尹志恒等[85-86]通过物理模型模拟方法也发现裂缝走向的品质因子大于裂缝法向。所以在包含定向裂缝的岩石里品质因子将随观测方位变化而变化,将这种现象称为衰减各向异性(Q-factor versus offset and azimuth,QVOA)[87-91]。VASCONCELOS等[92]也证实,衰减各向异性特征要强于速度方位各向异性,因此,利用QVOA反演有利于改善裂缝预测精度[93]。

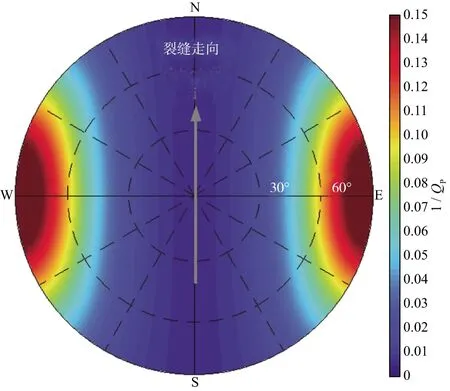
图11 地震波在垂直裂缝介质中传播时衰减随观测方位角的变化[5]

对于VFI介质,CHICHININA等[94-98]利用复值弱度、ZHU等[99-100]利用衰减各向异性参数均将衰减因子αQ近似表达为:

αQ≈A+B(φobs)sin2θ+C(φobs)sin4θ

(28)

其中,

B(φobs)=B0+B1cos2(φobs-φsym)

C(φobs)=C0+C1cos2(φobs-φsym)+
C2cos4(φobs-φsym)

并且很多数值实验和分析表明,在大多数情况下,裂缝法向的衰减系数大于裂缝走向的衰减系数。所以结合不同方位的衰减系数预测值和公式(28),利用最小二乘算法,可实现裂缝方位φsym的预测[90,101]。其中,不同方位衰减系数可以采用谱比法提取[98],具体地讲,计算地层上下界面同相轴频谱振幅比的自然对数,即:

(29)

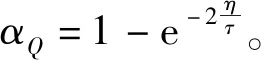
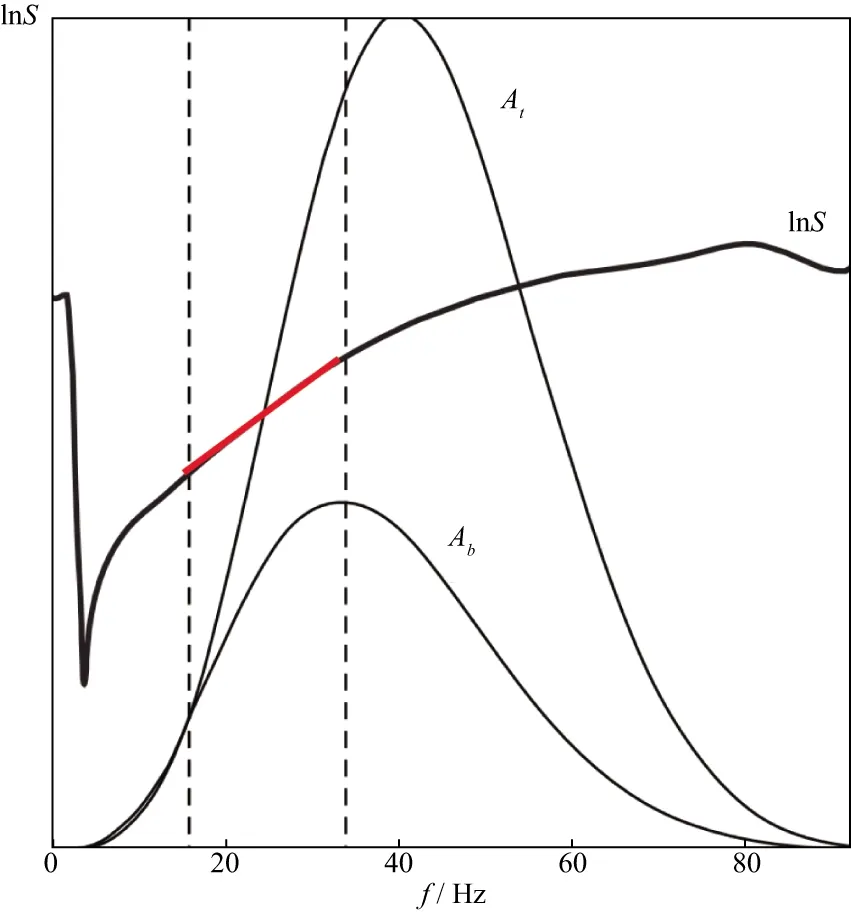
图12 目的层顶底界面同相轴的频谱振幅(At和Ab)及其振幅比的自然对数lnS随频率变化关系(红线标注代表频段,即lnS随f的线性变化段[101])

图13为衰减系数αQ与sin2θ的关系曲线。由图可见,衰减系数αQ对sin2θ的依赖性并非是二次的,所以基于公式(28)的裂缝方位预测结果可能存在较大的误差。因此,SABININ[101]和CHICHININA等[98]分别采用更为精确的衰减系数方程,即:

αQ=A+sin2θ[B0+B1cos2(φobs-φsym)]+

sin4θ[C0+C1cos2(φobs-φsym)+C2cos4(φobs-

φsym)]/{1+sin2θ[D0+D1cos2(φobs-φsym)]+

sin4θ[E0+E1cos2(φobs-φsym)+

E2cos4(φobs-φsym)]}

(30)

结合多方位衰减因子估计值,利用最小二乘算法实现裂缝方位估计。公式(30)中,A,B0,B1,C0,C1,C2,D0,D1,E0,E1和E2分别为储层属性的函数,为未知变量。

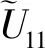
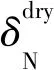
(31a)

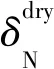
(31b)

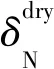
(31c)

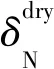
(31d)

C44=μb

(31e)

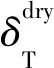
(31f)

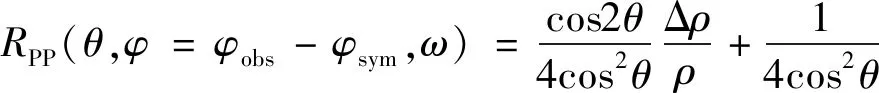
(32)

基于公式(32),采用分频地震反演方法[103]即可实现流体因子Ψn和干裂缝弱度参数的预测。

3 应用实例

某工区内A井钻遇优质页岩储层,该层段表现出早期水体较深、后期持续海退的沉积序列,水平层理、水平微断层以及高角度裂缝较为发育,可以将其等效为正交各向异性介质。所以我们采用MA等[41]提出的基于傅里叶级数展开的正交各向异性介质裂缝参数预测方法进行裂缝特征空间刻画。

首先,需要进行叠前方位地震数据处理。主要包括精细的排线扩散处理、震检组合效应的校正、反Q滤波、地表一致性处理、叠前剩余振幅补偿、精细的初至切除处理,分方位角道集集成处理、宽方位速度分析、分方位各向异性叠前偏移处理,方位叠前道集转换以及部分角度叠加等。最后得到6个方位地震叠加道集(0°～30°,30°～60°,60°～90°,90°～120°,120°～150°,150°～180°)以及每个方位包含一个入射角信息(16°)。采用约束稀疏脉冲反演将得到的五维地震数据转换为方位弹性阻抗体,利用电成像测井数据及地质先验信息模拟得到工区裂缝方位先验数据体,然后开展相关的裂缝密度和方位预测。

图14为该工区过水平井的地震剖面,白色箭头所指的地震同相轴为目的层反射轴。从地震剖面中很难看到裂缝密度的横向变化。图15为对应于图14 的裂缝密度预测结果,图中红色曲线代表水平井,曲线上的编号代表压裂段。图16为水平井各压裂段的破裂压力统计分析,显示第11段～第21段的破裂压力值较低,由于高裂缝密度将导致低的破裂压力,所以第11段～第21段的裂缝较为发育,与图15显示的裂缝密度预测结果比较吻合,说明裂缝密度预测结果较为合理。图17 为A井目的层段裂缝方位玫瑰统计分析,图17a 为成像测井解释结果,图17b为地震预测结果,可以发现预测结果和测井解释结果较为吻合,说明预测结果的正确性。

图14 过水平井的地震剖面

图15 过水平井的裂缝密度预测结果

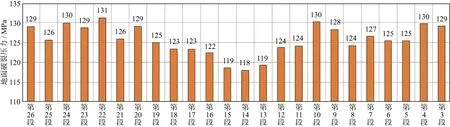
图16 水平井各压裂段的破裂压力统计分析

图17 A井目的层段裂缝方位玫瑰统计分析a 成像测井解释结果;b 地震预测结果

4 挑战和机遇

目前,随着缝洞发育的碳酸盐岩储层和页岩储层等非常规油气藏勘探开发的不断深入,裂缝参数五维地震预测已是国内外研究的热点和难点之一。同时,地震勘探目标从浅层迈向深层、从勘探迈向开发,从均匀弹性介质迈向非均匀复杂介质,由此对裂缝参数地震预测技术的精度和可靠性提出了新的要求。所以,根据目前油气勘探开发需求和现状以及五维地震裂缝预测技术的瓶颈问题,未来我们应该在以下3个方面开展进一步的研究。

1)五维地震数据中的裂缝信息比较微弱,在地震噪声的干扰下,实现复杂储层裂缝信息的准确提取是裂缝空间描述的难题之一,所以构建合理稳定的地震反演策略[38,104-106]是未来裂缝参数稳定预测的有效途径之一;

2)五维地震数据中包含丰富的方位、偏移距、振幅、频率和相位等信息,是地下储层裂缝、流体、孔隙度和矿物等物性参数的综合体现。探索这些信息与储层物性参数之间的关系,研究地震数据中地层物性参数的解耦方法,将有助于充分挖掘五维地震数据,有效提高裂缝检测和流体识别的精度;

3)裂缝储层反演技术目前基本假定介质弱各向异性和小弹性差异,从近似各向异性反射特征方程出发实现裂缝参数预测,然而地下介质复杂多变,各向异性程度范围较广,所以基于精确各向异性拟Zoeppritz方程[107-108]的裂缝储层描述将是未来油气勘探领域发展方向之一,以适应页岩等各向异性程度较大的目标。