四旋翼无人机旋翼对机身非定常气动干扰特性

朱毅飞 ,林德福 ,莫雳 ,叶建川

(1.北京理工大学 宇航学院,北京 100081;2.北京理工大学 无人机自主控制技术北京市重点实验室,北京 100081)

0 引言

目前,随着科技的发展和需求的不断增长,无人机产业迅速发展,在军用和民用方面,无人机的地位日益提高。多旋翼无人机作为无人机中最为广泛的一个种类,被广泛应用于军事侦查、军事打击[1-3]、灾害救援[4-6]、植物保护、物流运输、勘探等领域。由于这类飞行器旋转升力面多,耦合干扰强烈,非定常流动明显,亟需深入分析其气动特性的机理。然而当前多旋翼无人机虽然工程化样机及产品众多,但是机理研究尚有待进一步深化。

Hwang 等[7]采用数值计算方法,对不同构型无人机的气动特性和旋翼之间的气动干扰作了研究,采用滑移网格的方法来建立旋转的计算域,所得结果表明,气动干扰存在于悬停工况和前飞工况下,对于“+”构型和“×”构型,由于旋翼尾流诱导出的上洗气流和下洗气流特性不同而导致气动干扰的程度不同。进而对两种不同构型无人机旋翼之间的气动干扰进行了分析与对比,却未对旋翼与机身的干扰进行探究。

Barcelos 等[8]用势流法通过对比单独的旋翼,发现有关“+”构型和“×”构型之间力和力矩存在差异。结果表明,“+”构型无人机在顺时针旋转的前旋翼下有向右滚转的趋势,在逆时针旋转的前旋翼下有向左滚转的趋势。对于高前进比的“×”构型无人机,Breaststroke 布局(无人机对称面附近的前桨桨尖为后行)的旋翼效率略高于Bear-hug 布局(无人机对称面附近的前桨桨尖为前行),俯仰力矩配平需求较小。这种现象是由前行桨叶和后行桨叶诱导的上洗气流和下洗气流不对称导致的。“+”构型无人机比“×”构型无人机有更高的旋翼效率;“+”构型无人机比“×”构型无人机需要更多的滚转配平力矩,而“×”构型无人机则需要更多的俯仰配平力矩。

Luo 等[9]通过理论推导和计算流体动力学(CFD)仿真,得出了一种考虑尾迹干扰的四旋翼无人机前飞的数学模型,可用于飞行控制。研究表明,高速前飞模型可以通过Glauert 高速近似法[10]模拟为圆形固定翼,简化了旋翼在前飞过程中诱导处的复杂涡系,推导出了前飞状态下推力系数的计算公式,建立了考虑相互干扰的四旋翼前飞模型。但该研究未考虑非定常的气动干扰影响。

Fu 等[11]对旋翼进行补充实验,探究了滑流的气动特性,同时将拼接结构网格、滑移网格和雷诺平均纳维-斯托克斯(RANS)方程的计算研究作为依据来证明结论。结果表明,旋翼气动计算结果与实验结果吻合较好,能正确预测旋翼的滑流特性,旋翼之间的干扰对飞行器的性能有重要影响。

Misiorowaski 等[12]采用包含分离涡仿真模型和滑移网格的求解器AcuSolve 来求解Navier-Stokes 方程,以验证四旋翼无人机在侧向飞行条件下的性能。在10 m/s 前飞和低头5°俯仰角的工况下,开展2 个不同构型无人机——“×”构型无人机和“+”构型无人机的实验。在“×”构型无人机中,由于前桨的下洗作用,后桨存在拉力和扭矩损失,同时俯仰力矩也有所减小。在“+”构型无人机中,相比于单旋翼而言,东侧和西侧的旋翼由于北侧旋翼的上洗作用产生额外的拉力。由此可见,由于“×”构型无人机中南部旋翼的前部拉力损失较大,后桨需要更高的转速。

综合上述研究结果,气动干扰对无人机的气动特性将产生重要影响,其中作用在机身上的力和力矩是影响无人机飞行性能优劣的重要因素[13-16],然而目前,对无人机旋翼与机身瞬态气动干扰的研究仍显不足,无法获得无人机旋翼与机身气动干扰在时间上的分布规律及干扰的产生机理。

本文通过CFD 计算方法[15]对无人机旋翼和机身的气动干扰的瞬态变化进行分析,总结无人机旋翼和机身气动干扰的基本规律,并获得适用于不同需求下不同精度的拟合方程。

在计算方法上,一是采用四面体非结构网格划分计算域;二是使用滑移网格方法建立旋转域[9,17-19,23],模拟旋翼的旋转;三是在壁面附近采用棱柱网格,将第1 层网格节点布置在黏性底层之内,令y+＜5(y+为无量纲壁面距离,选取合适的y+值可以提高边界层的求解精度),来提高湍流的计算精度[21],捕捉流动细节。其次假设无人机机身及旋翼为刚体,忽略桨叶的形变及挥舞[12,20]。另外采用非定常计算方法[9,19],计算机身在旋翼旋转的每个周期内所受的力和力矩。最后,通过分析CFD 方法计算所得到的数据,获得了机身所受力和力矩的变化规律,并给出机身升力系数、阻力系数和俯仰力矩系数的拟合方法。本文结论是基于某一典型前飞工况得出的,但在不同飞行工况下无人机机身气动干扰特性的分析方法是一致的。本文可以为相似构型和工况的无人机机身气动干扰分析提供基本方法和参考。

1 模型及坐标系定义

无人机模型使用三维计算机辅助设计软件Solidworks 生成,其三视图以及轴测图如图1 所示。图1(c)中,R为旋翼半径,R=259.08 mm,d为旋翼中心到无人机纵向对称面的距离,d=313.85 mm,yh为机身宽度的一半,yh=45.00 mm,Ωf为前旋翼转速,Ωr为后旋翼转速。

图1 给出了无人机模型的部分尺寸和旋翼编号及旋转方向。在该模型中,螺旋桨选用中国TMOTOR 公司生产的MF2009 型多轴旋翼碳纤维塑料聚合物正反折叠桨,直径为20.4 in(518.16 mm)。螺旋桨旋转域直径为550 mm,厚度为30 mm。在图1(c)中,旋翼1、旋翼3 为逆时针旋转,旋翼2、旋翼4 为顺时针旋转[8]。无人机前飞时,为了保持其前飞姿态,需要额外的低头力矩来抵消恢复力矩,因此前飞时的无人机后旋翼转速一般高于前旋翼,而由于无人机的对称性,旋翼2 和旋翼3的转速相同,旋翼1 和旋翼4 的转速相同。需要特别说明的是,本文的研究是基于图1(c)中所标注的旋翼转向进行的。在该转向下,前旋翼靠近纵向对称面的一侧为前行桨,桨尖的局部速度大;后旋翼靠近纵向对称面的一侧为后行桨,桨尖的局部速度小。然而,若无人机的旋翼转向与本文所规定的相反,则前旋翼靠近纵向对称面的一侧为后行桨,后旋翼靠近纵向对称面的一侧为前行桨。在这种情况下分析出的最终结果有可能与本文所述结论有所不同,但计算和分析方法通用。因此,对于旋翼反转的情况,本文的内容仍然具有参考意义。

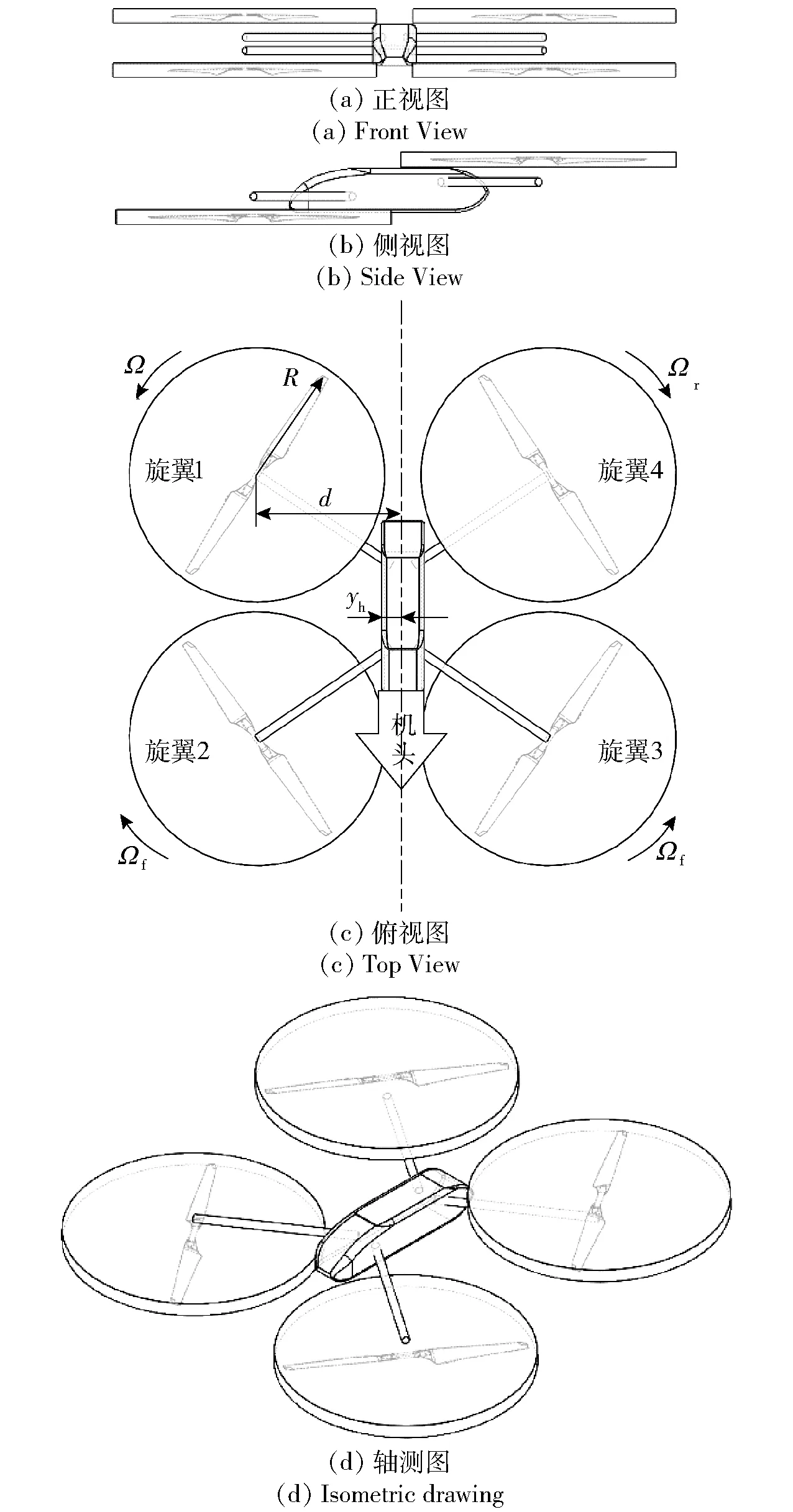
图1 无人机模型Fig.1 Quadcopter model

无人机机体坐标系Obxbybzb的定义如图2 所示:坐标系原点Ob位于无人机的质心处,xb轴指向无人机尾部,zb轴垂直于桨盘平面指向无人机上方,yb轴方向遵循右手定则。

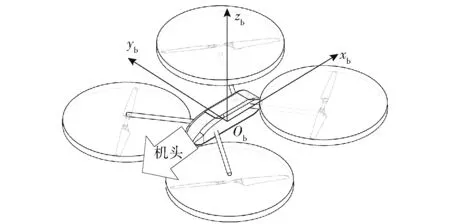
图2 无人机机体坐标系Fig.2 Body fixed coordinate

假设无人机无侧滑和滚转,速度坐标系Ovxvyvzv可以由机体坐标系Obxbybzb通过绕机体坐标系yb轴旋转α得到,α为攻角。

无人机在机体坐标系Obxbybzb和速度坐标系Ovxvyvzv下的力、力矩、速度、角度定义如图3 所示。图3 中:分别为无人机机身受力在机体坐标系xb轴、yb轴、zb轴上的分量;分别为无人机机身所受力矩在机体坐标系xb、yb、zb轴上的分量;Lf为无人机机身所受升力;Df为无人机机身所受阻力;分别为旋翼受力在机体坐标系xb轴、yb轴、zb轴上的分量;分别为旋翼所受力矩在机体坐标系xb轴、yb轴、zb轴上的分量;Lb为无人机旋翼所受升力;Db为无人机旋翼所受阻力;T为旋翼拉力;H为旋翼Hub 力;Q为旋翼扭矩;v∞为来流速度。

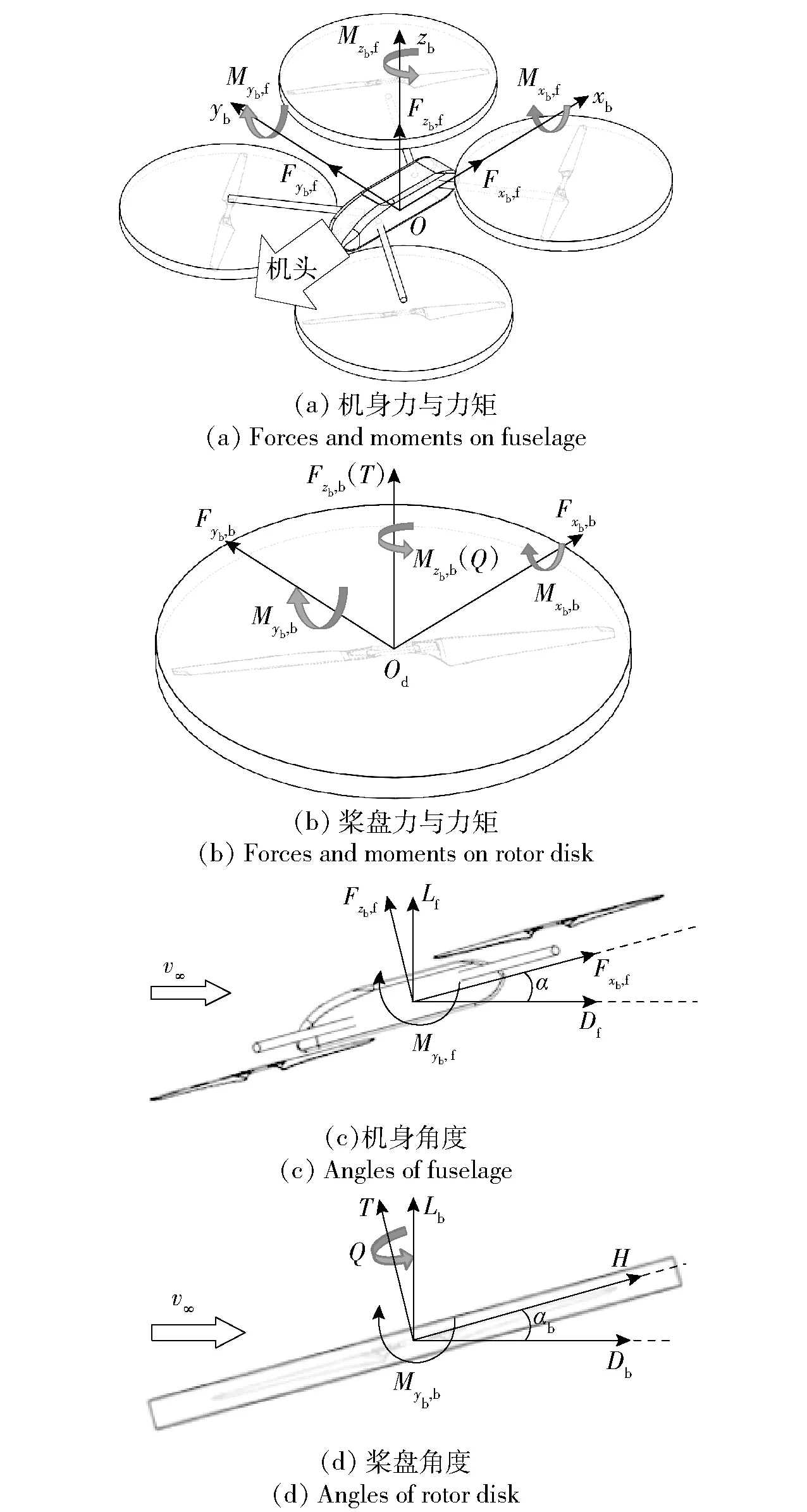
图3 无人机力、力矩、角度定义Fig.3 Definition of force,moment and angle

图3(a)、图3(c)为无人机机身的力、力矩、角度定义,图3(b)、图3(d)为无人机某一桨盘的力、力矩、角度定义。对于机身,机身所受力和力矩的方向与机体系正方向一致,阻力方向与来流方向一致,升力与阻力垂直,并且指向无人机上方。攻角为来流方向与机体坐标系xb轴之间的夹角,无人机低头时为正。对于桨盘,由于旋翼与机身之间没有安装角,机身攻角也是桨盘攻角,桨盘的力的方向定义与机身相同。

因此,可得机体坐标系与速度坐标系下相关力和力矩与攻角的转换关系:

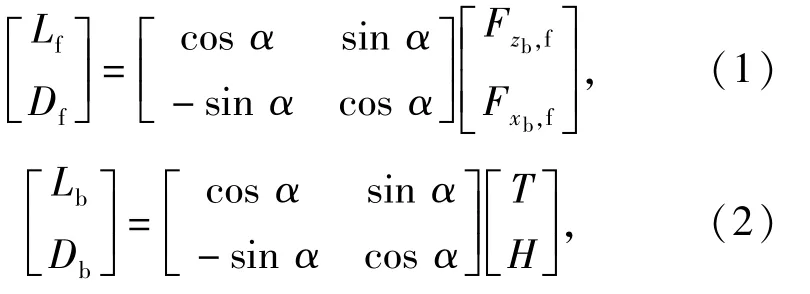
正升力提供的是使无人机上升的力,正俯仰力矩的作用效果使无人机抬头。由于无人机前飞时始终处于低头状态,单独机身的升力一般为负值。

由于本文是对无人机的非定常气动干扰进行探究,需要对于初始状态,即t=0 s 时刻下的状态进行特别说明。

图4 为无人机的初始状态,其中φf为前旋翼的方位角,φr为后旋翼的方位角,前、后旋翼的初始角度分别为φf0=55°、φr0=55°。

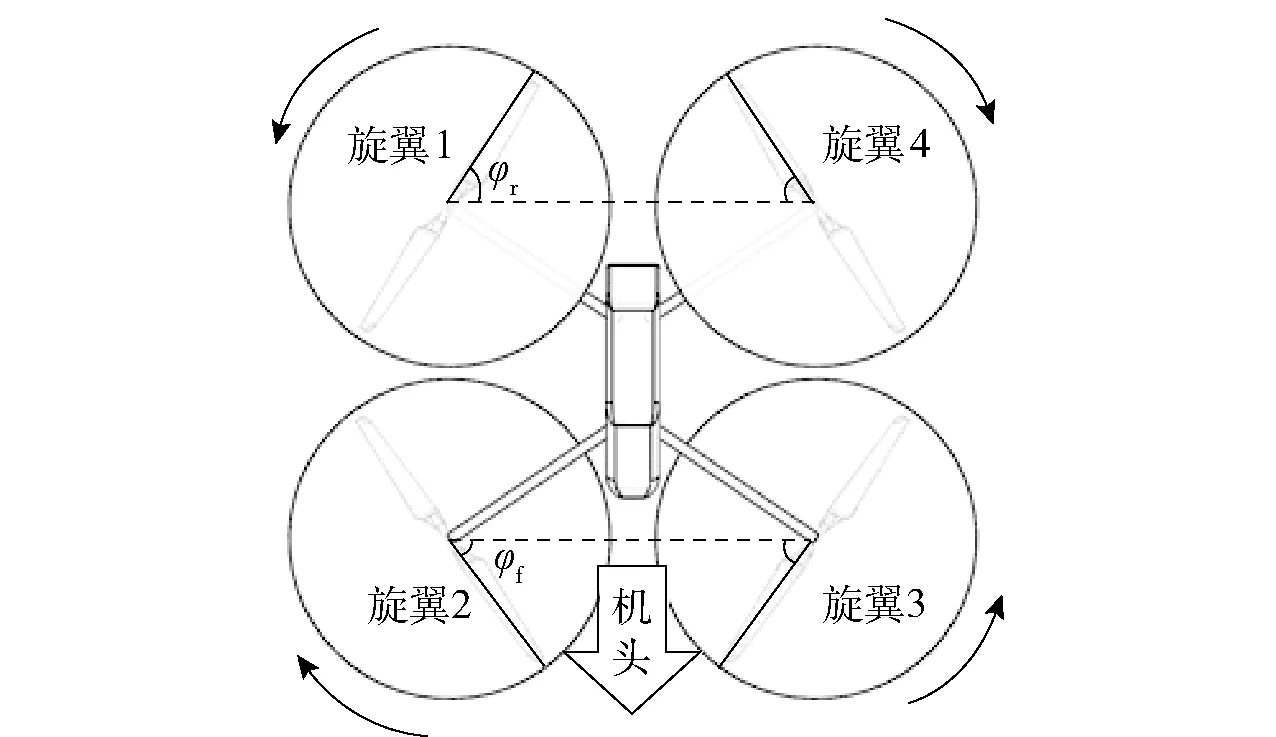
图4 无人机初始状态Fig.4 Initial state of UAV

2 CFD 计算方法

下面首先介绍本文采用的CFD 计算工况、求解模型以及网格生成策略,并进行网格敏感性分析,然后验证计算域划分的合理性,最后进行风洞实验验证以验证CFD 计算的准确性。

2.1 CFD 计算工况

无人机所处的飞行工况如表1 所示。表1 中,ff为无人机前旋翼的旋转频率,fr为无人机后旋翼的旋转频率。

表1 无人机飞行工况Tab.1 Flight conditions

定义f为无人机旋翼的旋转频率:

由于每片旋翼由2 片桨叶组成,旋翼每旋转半周即可被视作一个周期,旋转一周则对应2 个周期。

CFD 计算方法采用非定常流动模型,流动介质为不可压缩假设下的空气,气体密度为1.225 kg/m3,采用Pressure-Based Solver 求解器进行求解,湍流模型为可实现k-ε二方程湍流模型[9],该模型在标准k-ε模型的基础上提供了旋流修正,对旋转流动、流动分离计算有更好的性能,并采用半隐式压力速度耦合(SIMPLE)算法和2 阶迎风格式进行计算[23]。采用四面体的非结构网格来划分计算域,在靠近壁面处以及流动较为复杂的区域进行了加密处理,边界层通过棱柱网格来进行较为精确的模拟[21],保证近壁面处的y+＜5。采用滑移网格[9],用真实的运动对旋翼旋转进行相对精确的模拟。图5 通过对计算域中某一切面的展示说明了网格划分方法,展示了网格划分的效果。

图5 计算域网格划分Fig.5 Mesh generation of computational domain

由于需要对无人机旋翼对机身所产生的影响进行分析,基于图6(a)有旋翼模型建立了如图6(b)所示的纯机身模型,并在相同的计算条件下进行计算。

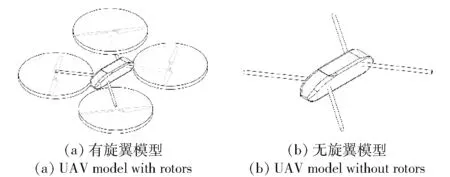
图6 有旋翼、无旋翼无人机模型Fig.6 UAV models with/without rotors

2.2 网格敏感性分析

为了提高计算效率,要求在保证精度的情况下网格数量尽可能少。因此,将2 种不同尺寸的网格在相同计算条件下进行结果对比,计算条件采用表1 中所示的速度和攻角。为了缩短计算时间,采用无旋翼的纯机身模型进行对比,计算结果如表2 所示。其中,CL,f、CD,f、CM,f分别为无旋翼无人机的机身升力系数、阻力系数、俯仰力矩系数。

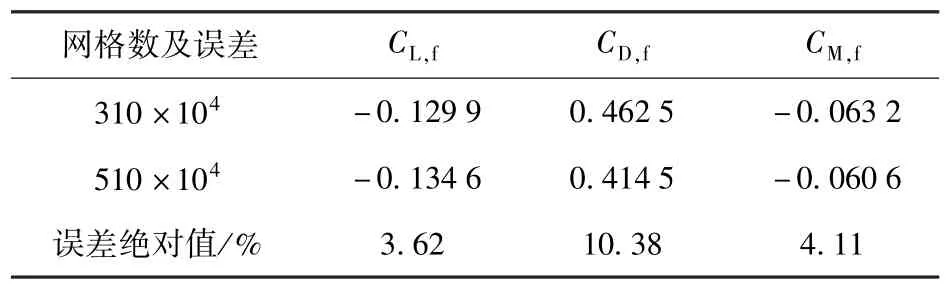
表2 网格敏感性分析结果对比Tab.2 Comparison of mesh sensitivity analysis results

由表2 可知,2 组网格数量分别为310 万和510 万,计算所得升力系数误差的绝对值为3.62%,阻力系数误差的绝对值为10.38%,俯仰力矩系数误差的绝对值为4.11%,因此可认为310 万网格计算的结果精度满足要求。

2.3 风洞实验验证

风洞实验在天津大学航空航天研究院进行。该风洞的截面尺寸为1.2 m×1.2 m,能提供的最大风速为30 m/s。由于风洞尺寸的限制,全尺寸无人机模型无法进入风洞进行实验,因此采用无人机所配螺旋桨进行单个旋翼的风洞测试,通过记录并对比单个旋翼的受力情况来验证CFD 计算方法的准确性[22]。

图7 为风洞和实验用旋翼。单个旋翼的测试条件如表3 所示,风洞实验时旋翼攻角与图3(d)中桨盘攻角的定义相同。

图7 风洞和实验用旋翼Fig.7 Wind tunnel and test rotor

表3 风洞实验测试条件Tab.3 Wind tunnel test conditions

采用德国ME-Meβsysteme 公司生产的MEK6D40 传感器来测量单个旋翼所受的拉力T,采样率为1 000 Hz,并对风洞实验数据和CFD 计算方法得出的数据进行对比,结果如表4 和图8 所示。

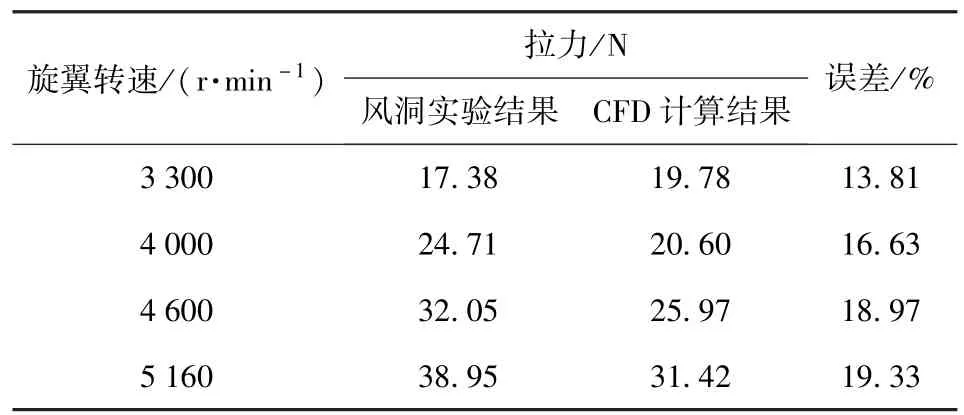
表4 风洞实验拉力对比Tab.4 Comparison of tensile forces T

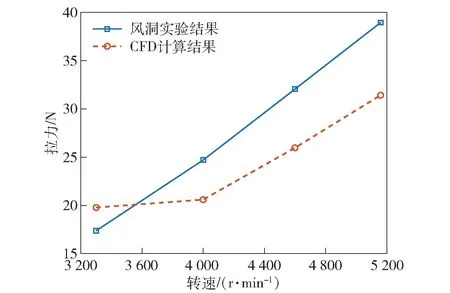
图8 不同转速下风洞实验与CFD 计算结果对比Fig.8 Comparison between wind tunnel test result and CFD calculated result at different rotation speeds

由表4 和图8 可知:CFD 计算结果与风洞实验数据误差在15%～20%之间,并且随着转速升高误差逐渐增大。本文中无人机旋翼的转速在3 200 r/min 左右,在该转速下误差大约控制在15%以内,满足精度要求,因此可以认为CFD 计算方法结果可靠。

3 气动特性分析

对无人机旋翼-机身气动干扰特性进行分析,包括机身的升力特性、阻力特性和俯仰力矩特性。对机身而言,若忽略旋翼所产生的诱导速度,则升力系数、阻力系数、俯仰力矩系数可以由(4)式～(6)式求得:

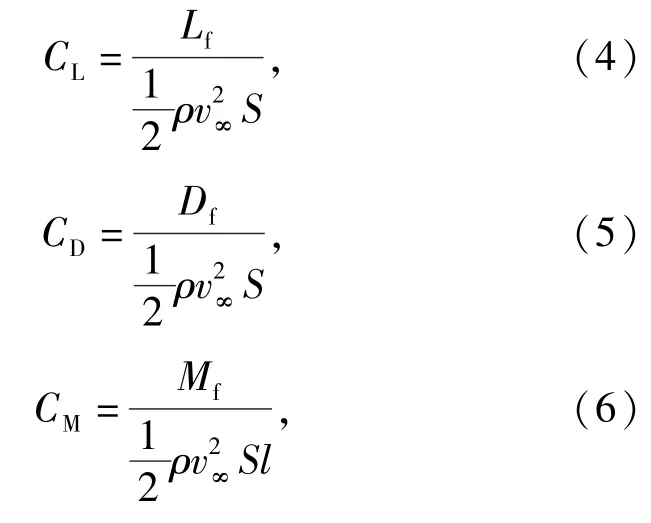
式中:ρ为空气密度;S为参考面积,取无人机机身前视图的投影面积;l为参考长度,取无人机机身的长度;Mf为俯仰力矩。对于CFD 计算结果,气动干扰产生的力和力矩系数可以通过将两个无人机模型各自的CFD 计算数据相减获得:

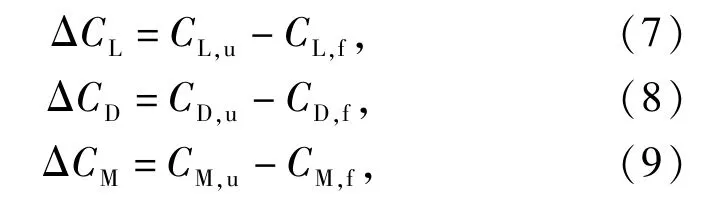
式中:CL,u、CD,u和CM,u分别为有旋翼无人机的升力系数、阻力系数、俯仰力矩系数。

3.1 升力特性分析

图9 为ΔCL快速傅里叶变换(FFT)后的结果。由图9 可知,频率最低的峰值出现在103.8 Hz 和111.1 Hz 处,且频率峰值都是成对出现,高频分量与最低频率呈倍数关系,且高于2 阶的模态其对ΔCL周期变化的贡献以近似线性的规律逐渐减小。对比表1 的结果,可以发现2ff=104.30 Hz≈103.8 Hz,2fr=110.77 Hz≈111.1 Hz。

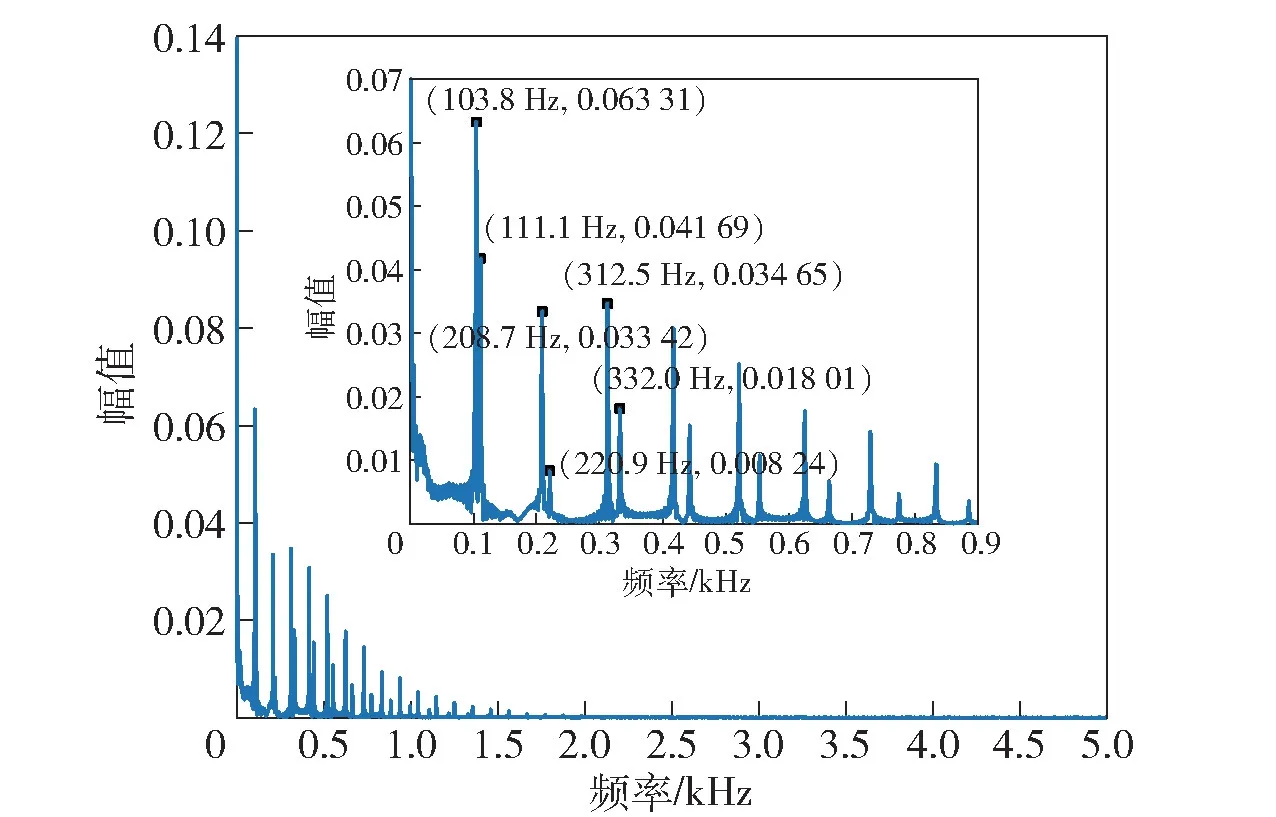
图9 ΔCL FFT 结果Fig.9 FFT results of ΔCL

FFT 结果的最低频分量与无人机前后旋翼的转速频率的2 倍近似相等,即ΔCL变化的1 阶模态与无人机旋翼的转速有直接关系。从结果的幅值来看,前旋翼对于机身升力的影响显著大于后旋翼;频率越高,对应分量的影响越小。因此,旋翼对升力的影响可以用傅里叶级数来表示如下:

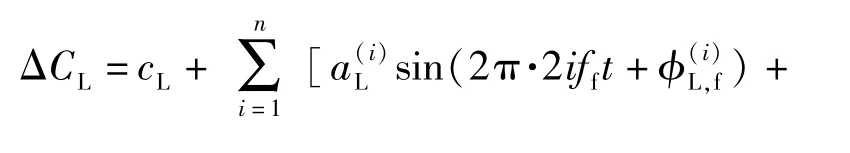
表5 和表6 对FFT 所得到的幅值结果与拟合方程中的系数做了对比,为了使结果更直观,取拟合方程系数的绝对值进行比较,计算出的误差为两项变化的绝对值。结果表明,拟合系数与FFT 获得的幅值误差普遍在7%以下,最大不超过15%,吻合情况良好。故推测,前5 阶模态的信息能够反映ΔCL变化绝大部分信息,忽略高于5 阶模态不会对拟合精度造成大的影响,前5 阶模态能够精确地体现出旋翼对机身的气动干扰特点。

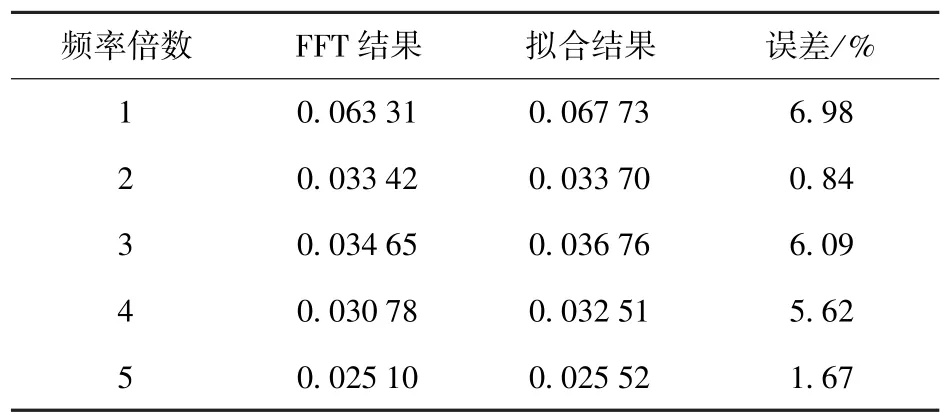
表5 前旋翼拟合系数对比Tab.5 Comparison of fitting coefficients of front rotor

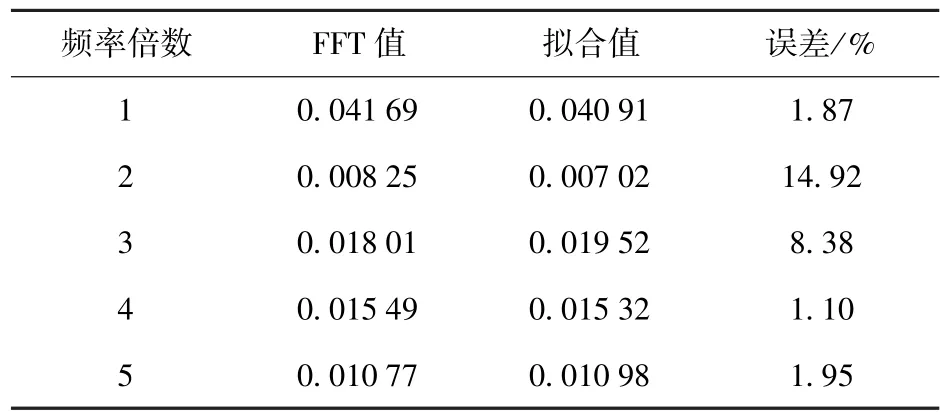
表6 后旋翼拟合系数对比Tab.6 Comparison of fitting coefficients of rear rotor

根据时间t和前后旋翼转速的关系

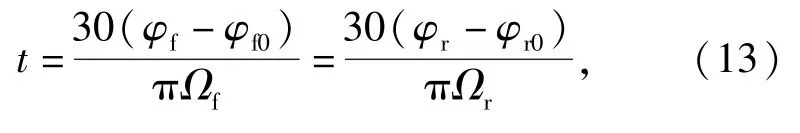
可得拟合后的结果,如图10 所示。

图10(a)为前旋翼方位角在2 000°～8 000°之间ΔCL的傅里叶级数拟合结果以及原始数据。由图10 可知,1～5 阶模态傅里叶级数能够很好地描述无人机机身ΔCL的影响,拟合曲线能反映原始数据的大部分信息,并且描述原始数据的变化细节。

为了进一步简化方程的形式,在只保留单独1 阶模态信息的情况下,ΔCL可以写为

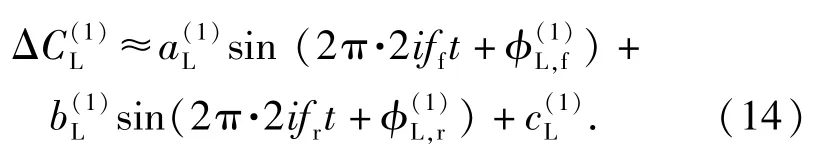
因此,拟合方程可写为

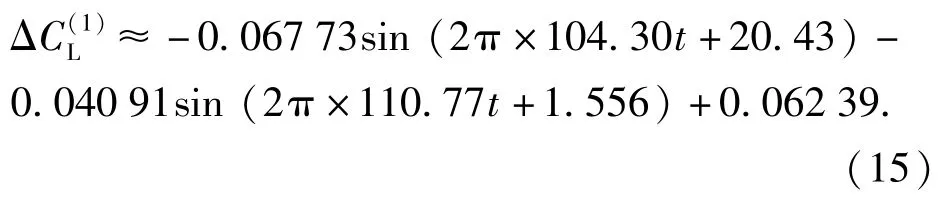
在忽略2 阶及更高阶模态以后,ΔCL的拟合结果如图11 所示。与图10 相比,图11 中拟合曲线的变化幅值有所减小,这是因为高阶模态信息被剔除后,拟合曲线失去了这一部分对幅值的贡献,从而导致了变化幅值的减小。同时可以发现,拟合曲线中的诸多细节被忽略。例如图11(b)中红圈所示的部分,其变化趋势在图10(b)中能够通过高阶模态项在一定程度上被表达出来,但单1 阶模态无法描述该变化情况。然而,虽然单1 阶模态相比1～5 阶模态的拟合结果而言无法描述出原始数据的一些细节变化情况,但仍能反映出ΔCL的总体变化趋势,即ΔCL总体上由2 个周期性变化构成,其中,短周期描述了ΔCL随旋翼旋转的变化规律,长周期描述了前、后旋翼转速差的影响,ΔCL的长、短周期均以正弦规律随时间变化。

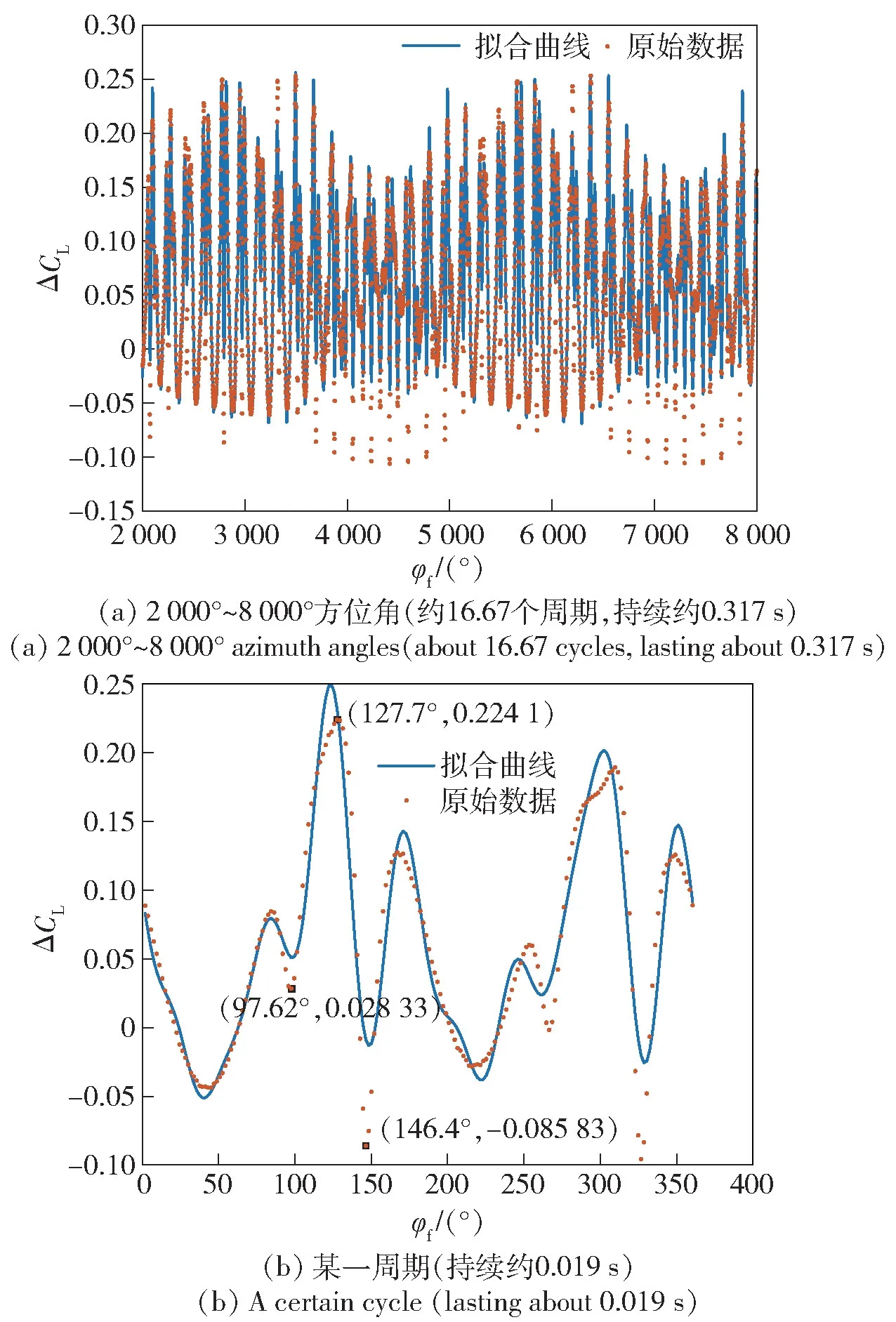
图10 ΔCL的1～5 阶傅里叶级数拟合结果Fig.10 Fitting result of the first-fifth-order Fourier series of ΔCL

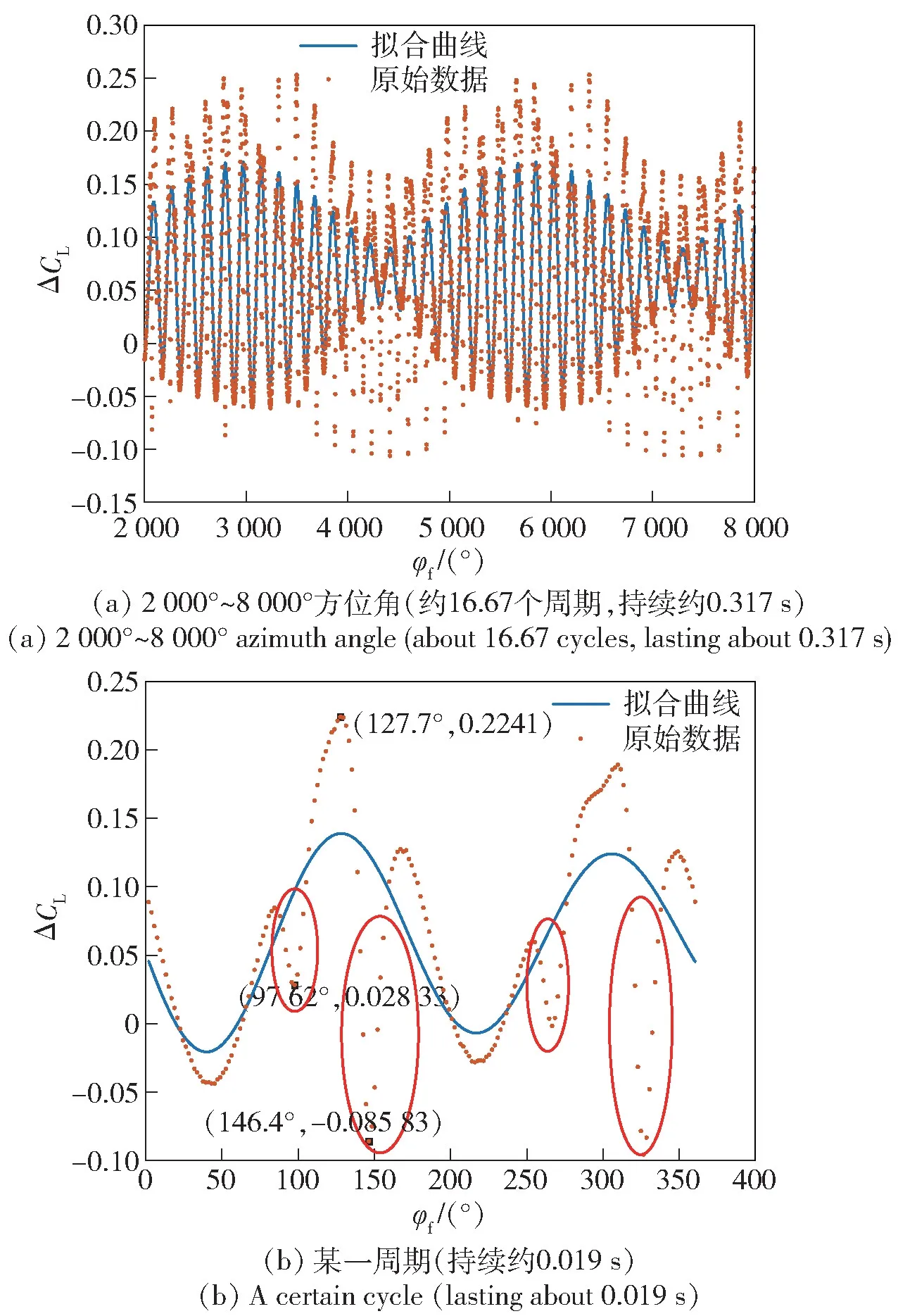
图11 ΔCL的单1 阶傅里叶级数拟合结果Fig.11 Fitting result of single first-order Fourier series of ΔCL

3.2 阻力特性分析

ΔCD的拟合结果如图12 所示。由图12 可以看出,ΔCD与ΔCL有相似的频率分布,1 阶模态和2 阶模态对ΔCD的贡献相似,高于2 阶的模态其对ΔCD周期变化的贡献以近似线性的规律逐渐减小。ΔCD的傅里叶级数可以写为

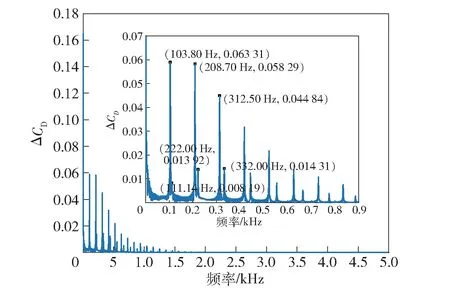
图12 ΔCD的FFT 结果Fig.12 FFT results of ΔCD

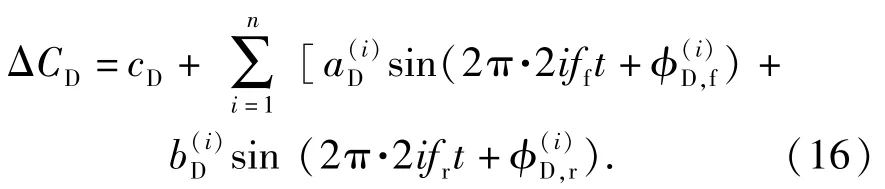
同样,保留前5 阶模态的信息,(16)式可以写为

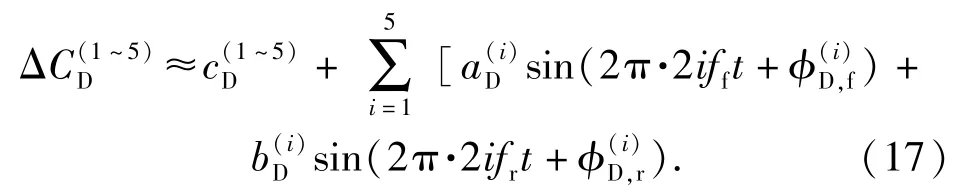
经拟合,可得(17)式的具体表达式为

图13 为前旋翼方位角在2 000°～8 000°之间ΔCD的傅里叶级数拟合结果以及原始数据。由图13中可知,包含1～5 阶模态的拟合曲线能够很好地与CFD 计算方法结果吻合,能反映出ΔCD变化的细节部分。从原始数据的走势分析,若采用单1 阶模态的方程拟合,则拟合曲线与原始数据之间会存在较大的差别。

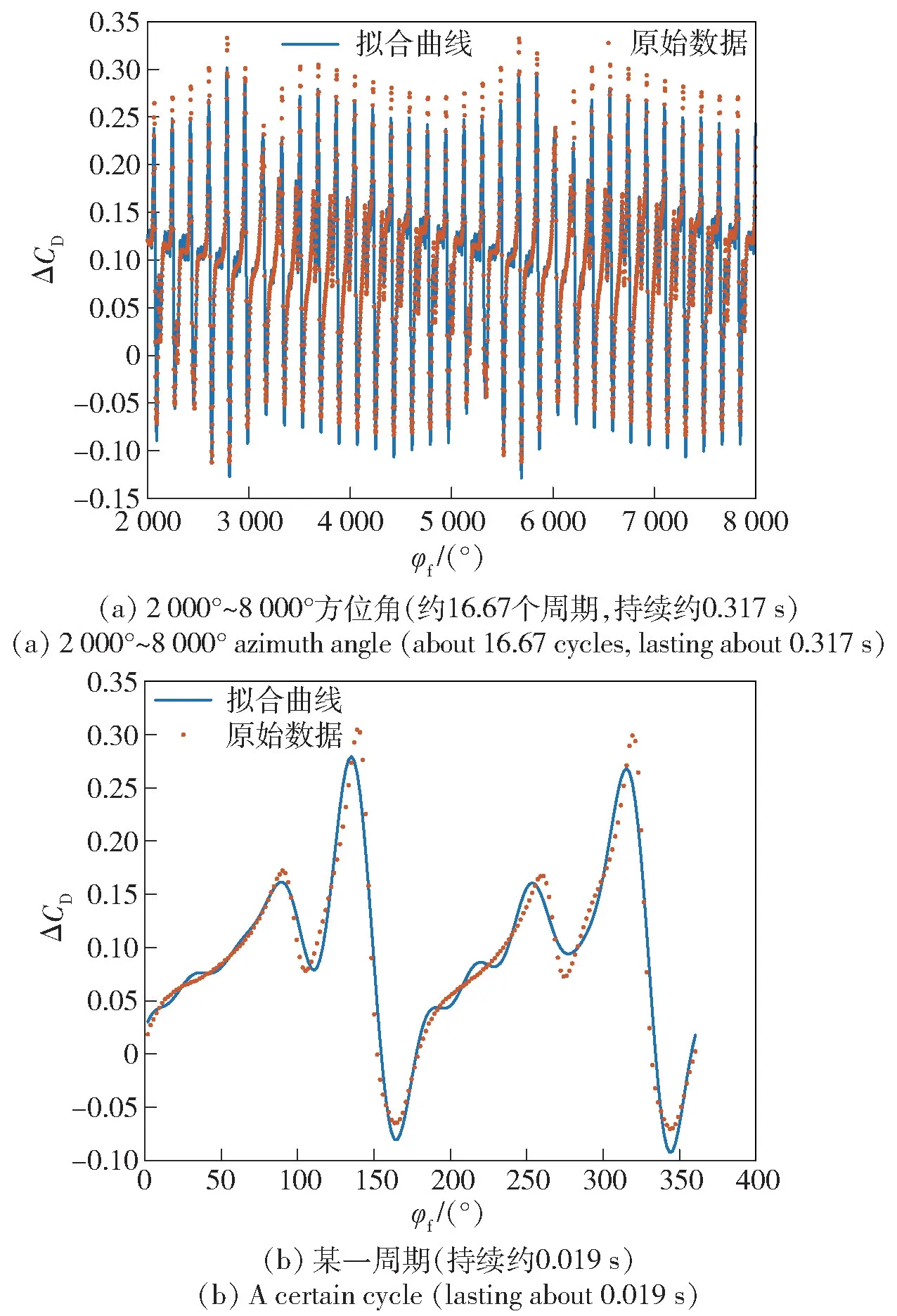
图13 ΔCD的1～5 阶傅里叶级数拟合结果Fig.13 Fitting result of the first-fifth-order Fourier series of ΔCD

表7 计算并归纳了1～5 阶模态傅里叶级数拟合结果与原始数据的R2值。从表7 中数据来看,1～3 阶模态下的拟合结果所对应的R2值为0.816 0,大于0.8。因此,为简化拟合方程形式同时保证拟合精度,保留1～3 阶模态信息,经拟合,包含1～3 阶模态信息的ΔCD傅里叶级数拟合结果可以写为

表7 ΔCD各阶模态傅里叶级数拟合结果R2值Tab.7 R2 of fitting results of ΔCD with different Fourier series

图14 为包含1～3 阶模态信息的ΔCD傅里叶级数拟合结果,与ΔCL相比,结果更为复杂。图14(b)与图13(b)的周期相同,图14(c)为另一周期内的结果。由图14 可知,相比于1～5 阶模态的傅里叶级数的拟合结果,1～3 阶模态能够在一定程度上描述ΔCD的变化规律,但在幅值上有所损失,并且1～3 阶模态拟合曲线的峰值所对应的相位与原始数据之间存在少量偏差。通过对比图14(b)和图14(c)不难发现,随着时间的推移,ΔCD在不同周期内的变化规律也有所不同。图14(b)中,ΔCD的第1 个突变出现在φf=105.1°,第1 个峰值出现在φf=138.9°;在图14(c)中,ΔCD的第1 个突变出现在φf=65.71°,第1 个峰值出现在φf=140.8°。图14(b)、图14(c)所对应的周期中,突变出现的位置存在大约40°的相位差,但峰值与谷值的相位差距很小。表明ΔCD的变化中,波峰和波谷的变化是由于前旋翼的旋转所造成的,而突变的产生与其他高阶模态的信息有关。因此,1～3 阶模态能够反映出ΔCD的总体变化,但无法准确地描述突变的产生。根据图13 中的结果,对于产生突变的高阶模态,至少需要1～5 阶傅里叶级数才能进行较为准确的拟合。

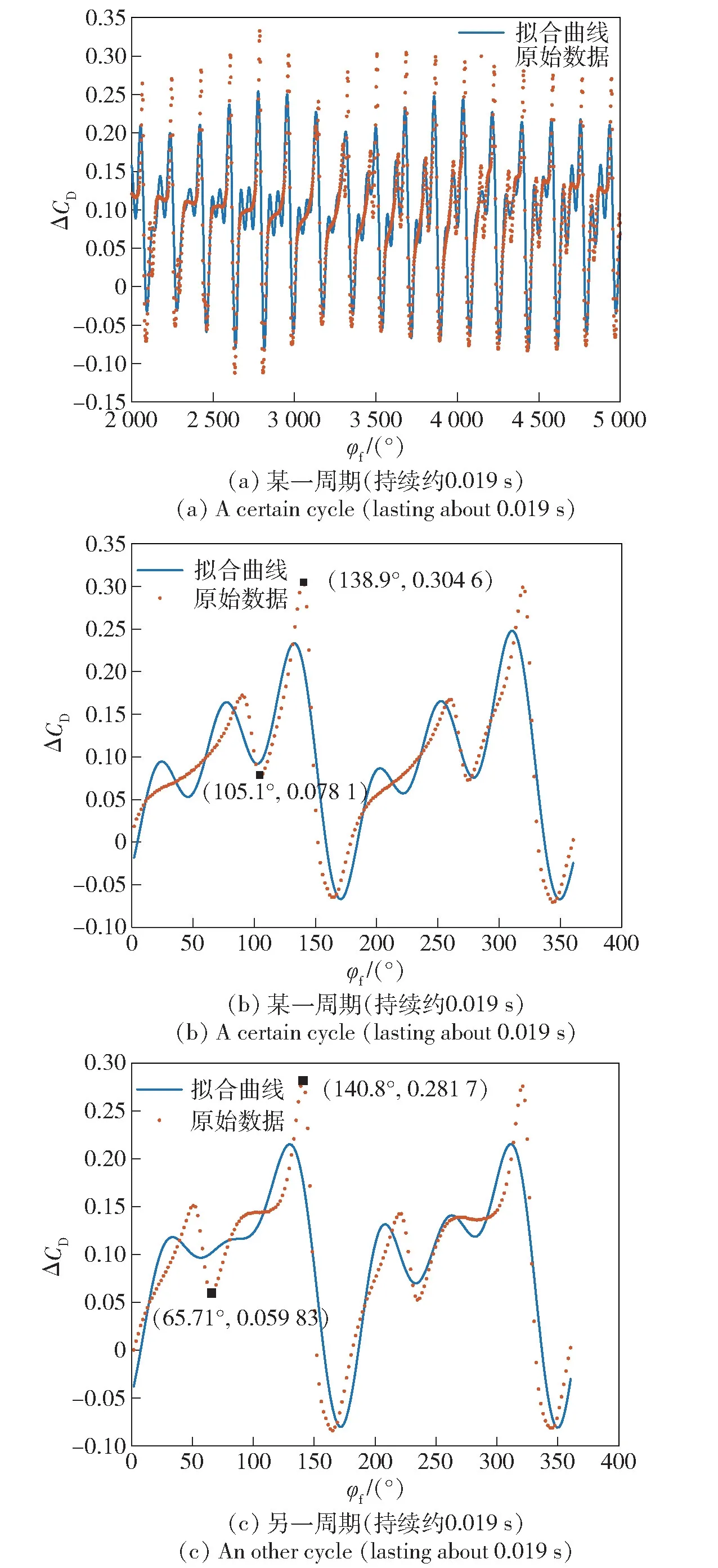
图14 ΔCD的1～3 阶傅里叶级数拟合结果Fig.14 Fitting result of the firsst-third-order Fourier series of ΔCD

3.3 俯仰力矩特性分析

图15 为ΔCM在FFT 后得到的频率分布。由图15 可知,ΔCM的频率分布与ΔCL和ΔCM的规律一致,最低频分量都为103.8 Hz 和111.1 Hz,且高频分量为最低频分量的倍数,高于2 阶的模态其对ΔCM周期变化的贡献以近似线性的规律逐渐减小。但不同的是,1 阶模态对ΔCM产生的影响小于2～5 阶,且对于1 阶模态而言,后旋翼的贡献略大于前旋翼。同样,ΔCM可以用形如(20)式的傅里叶级数描述出来:

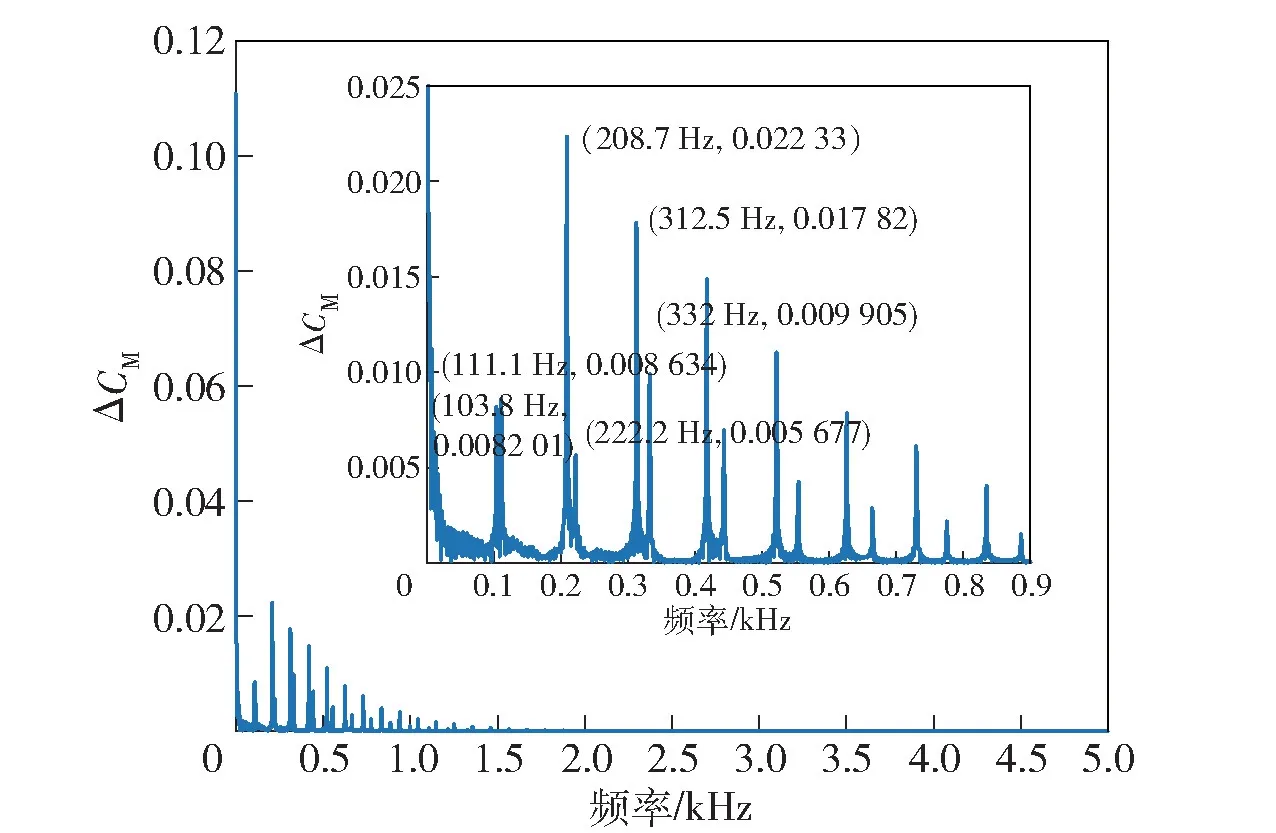
图15 ΔCM的FFT 结果Fig.15 FFT result of ΔCM

图16(a)为前旋翼方位角在2 000°～8 000°之间ΔCM的傅里叶级数拟合结果以及原始数据,图16(b)为图16(a)中某一个周期结果的局部图,该周期与图10(b)中的周期相同。由图16 可知,除最小值附近的某些数据点外,1～5 阶傅里叶级数能够较好地反映出ΔCM的变化规律,包括一些变化细节。与图8 中的ΔCL对比,发现图16(b)中ΔCM第1 个波峰和第1 个波谷出现的相位与ΔCL相同。由此可以推断,ΔCM在φf=97.62°和φf=146.4°出现的突变是由于机身升力的突变所引起的,在φf=97.62°时,造成机身升力减小的因素出现在无人机质心后部;在φf=146.4°时,造成机身升力减小的因素出现在无人机质心前部,因此造成了ΔCM先突然增大、后突然减小的现象。

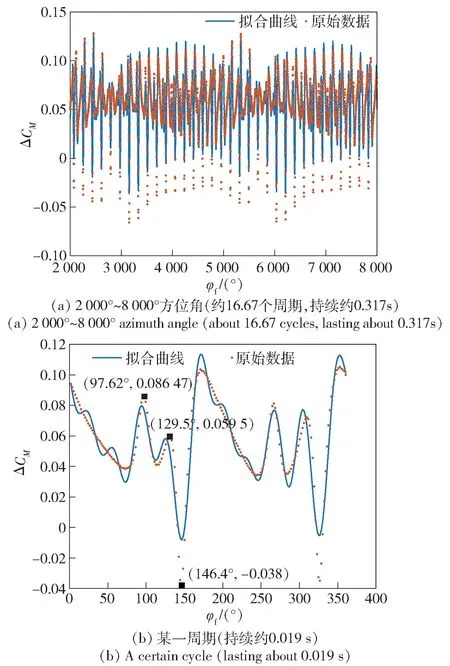
图16 ΔCM的1～5 阶傅里叶级数拟合结果Fig.16 Fitting result of the first-fifth order Fourier series of ΔCM

由图15 所得结论,ΔCM受2 阶模态的影响显著大于1 阶模态,因此为简化拟合方程,在只保留单2 阶模态信息的情况下,ΔCM的傅里叶级数拟合结果为

图17 所示的拟合结果表明,单2 阶模态傅里叶级数的拟合结果能够反映ΔCM的变化趋势,但无法准确描述出波峰和波谷的幅值,并且在相位上也有误差。总体上来说,ΔCM与正弦函数的变化趋势相似,并且变化频率与基频的2 倍相关性较高。

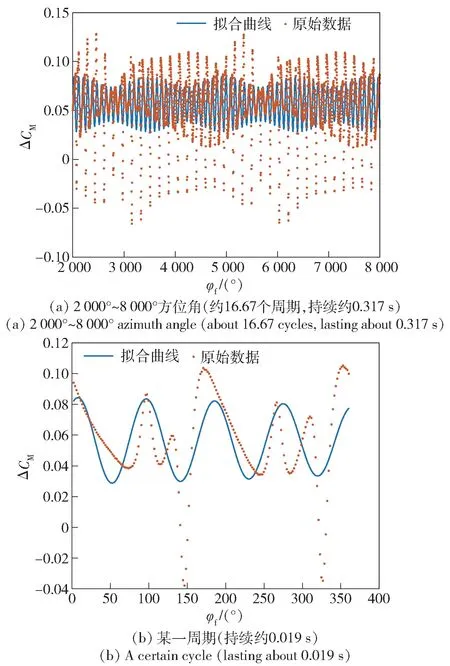
图17 ΔCM的2 阶傅里叶级数拟合结果Fig.17 Fitting result of the second-order Fourier series of ΔCM

为了更精确地描述出ΔCM的变化,总结了包含各个模态方程拟合结果的R2值,如表8 所示。

表8 ΔCM各阶模态傅里叶级数拟合结果R2值Tab.8 R2 of fitting results of ΔCM with different orders of Fourier series

从表8 中数据来看,1～4 阶模态的拟合结果所对应的R2值0.818 7 大于0.8。这说明方程至少包含1～4 阶的模态信息才能够以较高的精度反映原始数据的变化情况。保留1～4 阶模态信息,经过拟合,ΔCM的傅里叶级数拟合结果为

图18 为1～4 阶模态傅里叶级数的拟合结果。从图18 中可以看到,拟合结果能够较为精确地描述ΔCM的变化趋势。与图17 中的拟合曲线相比,1～4 阶模态包含的信息能够更好地描述波峰和波谷的幅值,反映出了无人机机身升力突变对俯仰力矩造成的突变影响,并且拟合曲线在相位上的误差也有所减小。因此,对于ΔCM而言,最少需要1～4 阶模态的信息才能反映变化的细节,而单2 阶模态只能够描述出ΔCM在周期变化上的规律。若只对ΔCM的周期变化感兴趣,则2 阶模态可以满足要求;若需要获得更多关于ΔCM的变化信息,则最少需要1～4 阶模态。

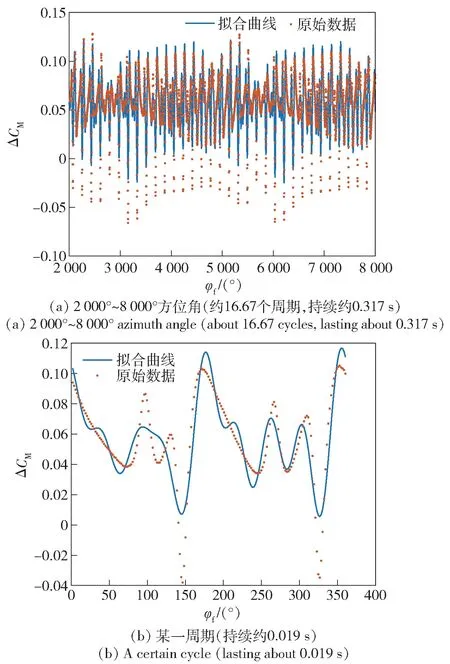
图18 ΔCM的1～4 阶傅里叶级数拟合结果Fig.18 Fitting result of the first-fourth-order Fourier series of ΔCM

4 结论

本文采用数值计算方法,对典型构型的四旋翼无人机旋翼与机身之间的非定常气动干扰进行了分析。通过对CFD 计算结果的拟合与分析,得出如下主要结论:

1)无人机机身升力系数的变化ΔCL与无人机旋翼的旋转周期密切相关,并且前旋翼的影响程度显著大于后旋翼。ΔCL变化的1 阶模态频率为无人机前、后旋翼的旋转频率的2 倍,而更高阶模态的频率则是1 阶模态频率的整数倍频。

2)无人机机身升力系数变化ΔCL可以用1～5 阶傅里叶级数较为精确地描述。单1 阶模态的傅里叶级数能够描述出ΔCL的总体变化趋势。总体上说,ΔCL由2 个周期变化构成,其中,短周期描述了ΔCL随旋翼旋转方位角的变化规律,长周期描述了前后旋翼转速差的影响。ΔCL的长短周期均以正弦规律随时间变化。

3)无人机机身阻力系数的变化ΔCD可以用1～5 阶傅里叶级数较为精确地描述出来。其中1～3 阶傅里叶级数能够描述出ΔCD的总体变化情况。前旋翼对于ΔCD的影响较大,影响ΔCD曲线的波峰和波谷,但其中的突变需要更高阶模态的信息来体现。

4)无人机机身俯仰力矩系数的变化ΔCM可以用1～5 阶傅里叶级数较为精确地描述出来。ΔCM的突变是由于机身升力的突变所引起的。ΔCM受2～5 阶模态的影响较大。其中2 阶模态能够描述出ΔCM在周期变化上的规律,而1～4 阶模态包含的信息能够更好地描述波峰和波谷的幅值,反映出了无人机机身升力突变对俯仰力矩造成的突变影响。总体而言,ΔCM与正弦函数的变化趋势相似,并且变化频率与基频的2 倍相关性较高。

5)对于无人机机身升力、阻力、俯仰力矩受旋翼气动干扰影响的规律,可以根据实际应用中所关注的重点来灵活选取拟合模型。若重点关注其细节变化,则需要采用包含更多模态信息的高阶傅里叶级数拟合结果;若只关心其周期变化的规律,不着重考察变化中的细节,则可以采用相对简化的模型来代替。