基于Total-FETI法的混凝土损伤分析子区域剖分研究

邱莉婷 马福恒 沈心哲

摘要：在整体有限元撕裂对接法和隐式梯度损伤模型结合的基础上，针对损伤子区域模拟的高精度要求和混凝土损伤扩展路径的不确定性问题，通过引入基于非局部损伤应变的子区域自适应更新方法，结合子区域更新误判修正，实现了混凝土损伤失效过程非线性子区域的高精度有限元网格自适应更新。同时，对L型混凝土试件进行不同子区域剖分数量和子区域分解形式的数值试验对比分析。研究结果表明：模型不存在子区域分解敏感性;子区域剖分数量越多，或者子区域分解方式与损伤扩展路径相适应时，高精度有限元网格子区域的自适应更新数量越少，模型计算规模减小明显;此外，子区域界面节点的增加对计算规模削减的影响较小，模型整体计算效率提高明显。研究结果可为混凝土损伤分析的并发多尺度数值计算提供参考。

关 键 词：混凝土损伤; 隐式梯度损伤模型; 整体有限元撕裂对接法; 子区域自适应更新; 子区域分解形式; 计算效率

中图法分类号： TU43

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2022.04.028

0 引 言

混凝土结构服役过程中在结构突变区域容易出现局部应力集中现象，其工程结构的失效往往源于局部构件的细观缺陷和损伤局部化行为[1-2]。进行混凝土结构的稳定性和强度分析时不仅要把握结构整体力学响应，同时也应该重视混凝土的损伤萌生、扩展和失效过程[3]。损伤力学作为模拟连续介质逐步劣化过程的有效分析方法，可反映结构从完整连续介质结构体到局部损伤萌生直至整体失效的全过程[4]。随着损伤的不断积累，混凝土因其准脆性特性将出现应变局部化和应变软化行为[5]，为保证计算精度，该区域有限元网格的精细化程度也需要不断提高。混凝土作为典型的准脆性材料[6]，其细观结构由骨料、硬化水泥砂浆和二者间的界面黏结带组成[7-8]。混凝土的断裂破坏是细观层次上损伤积累与宏观尺度上裂紋失稳扩展交织发展的复杂过程[9]。混凝土结构的损伤扩展路径具有不确定性[10]，数值计算过程需要不断地进行网格自适应更新，以满足对损伤局部化区域力学特性的准确把握。

本文将整体有限元撕裂对接法和隐式梯度损伤模型相结合，在损伤子区域高精度有限元网格自适应更新的基础上，开展混凝土损伤失效过程自适应、多尺度区域分解模拟，并开展子区域分解影响研究，为模型混凝土损伤区域的高精度模拟和损伤扩展路径的不确定性问题研究提供解决途径。

1 混凝土损伤分析的Total-FETI法

1.1 基于隐式梯度损伤模型的Total-FETI法

隐式梯度损伤模型属于特殊的非局部损伤模型[11-12]，其将非局部模型中的权函数替换成格林（Green）函数[13]，该模型结合了空间相互作用与梯度公式的计算效率，操作更为简单，也称修正的Helmholtz’s方程：

εeq-clSymbolQC@2εeq=ε（1）

式中：非局部等效应变εeq不是由等效局部应变ε和它的导数显式描述的，而是作为包含方程（1）的边值问题和近似边界条件的解[14];梯度参数为内部长度参数l的函数。

有限元撕裂对接法（finite element tearing and interconnecting method，FETI）属于采用局部边界条件的不重叠区域分解法[15-16]，其并行计算的收敛速度与子区域的数量相互独立，可以将原求解问题划分成更多的子区域进行求解，且可以保证较高的求解效率[17]。整体有限元撕裂对接法（Total-FETI）在有限元撕裂对接法基础上将拉格朗日算子同时用于子区域界面连接和狄利克雷边界条件的施加[18-19]，可简化子区域刚度矩阵的求逆过程。非线性有限元撕裂对接法的线性方程系统和子区域Ω（s）间的位移连续条件可表述为

A（s）kδu（s）k+1+B（s）Tδλk+1=f（s）ext-B（s）Tλk-f（s）int，k（u（s）k）（2）

Nss=1B（s）u（s）k+Nss=1B（s）δu（s）k+1=0（3）

式中：A（s）是切线刚度矩阵;δu（s）和δλ（s）分别为位移增量和拉格朗日乘子增量;布尔矩阵B（s）由子区域界面的布尔矩阵和狄利克雷边界条件对应的布尔矩阵按行串连构成;f（s）ext为外力向量;f（s）int为内力向量;Ns为子区域数量。

隐式梯度损伤模型的非局部等效应变εeq在Total-FETI中可通过对给定子区域界面的拉格朗日算子进行修正实现：

λd=λλεeq（4）

式中：λεeq为非局部等效应变对应的自由度。

再通过扩展布尔矩阵B（s）将λd装配到相应位置，布尔矩阵Bd （s）由原来Total-FETI的子区域界面的布尔矩阵B（s）和非局部等效应变对应的布尔矩阵B（s）eq按行串连构成：

B（s）d=B（s）B（s）eq（5）

1.2 FETI的局部子区域自适应更新

本文混凝土结构的损伤分析采用隐式梯度损伤模型。对于各个非线性子区域的实时判别，可以根据特定加载步的各子区域的非局部等效应变最大值ε（s），maxeq与损伤发生时的应变阈值k0的相对关系进行。仅当子区域的非局部等效应变最大值ε（s），maxeq大于等于应变阈值k0时，损伤才会发生。这里，对子区域Ω（s）遍历其所有节点n得到其非局部等效应变最大值ε（s），maxeq，t和非局部等效应变最小值ε（s），mineq，t：

ε（s），maxeq，t=max（εeqi），i=1，2，…，n（6）

ε（s），mineq，t=min（εeqi），i=1，2，…，n（7）

记加载步t和加载步t+1所对应的非局部等效应变差值的预测值为Δε（s）t，则加载步t+1的非局部等效应变最大值ε（s），peq，t+1的实时预测值为[20]

Δε（s）t=max（ε（s），maxeq，t-ε（s），mineq，t-1，ε（s），mineq，t-ε（s），maxeq，t-1）（8）

ε（s），peq，t+1=ε（s），maxeq，t+Δε（s）t（9）

引入基于层级多尺度的子区域自适应更新方法[21]进行非线性子区域实时更新。首先，通过边值问题求解以获取被替换子区域的最近变形;然后，进行整体区域的重新平衡迭代以消除由于子区域更新导致的残余应力;进一步地，采用尺度间的线性多点约束（interscale linear multi-point constraints，ILMPCs）[21-22]进行子区域更新后的非协调界面连接，使得不同精细度有限元网格子区域可在同一个有限元计算模型中共存。

对于两个网格精细度不一致的子区域，其尺度间的线性多点约束用矩阵形式可表示如下[23]：

Pu=[P（1） P（2）]u（1）u（2）=0 （10）

式中：u（s）为子区域Ω（s）的位移向量;矩阵P（s）由线性多点约束组成，建立了子区域更新后新增界面节点与邻接子区域节点间的联系，即高精度有限单元的节点自由度通过邻接子区域交界面处单元的形函数插值求得。

这一系列尺度间的线性多点约束施加可以通过在Total-FETI中用拉格朗日乘子添加额外数量的方程完成。通过定义一个修正的布尔矩阵B（s）来实现。修正后布尔矩阵B（s）由B（s）d和约束矩阵P（s）按行串连组成：

B（1）B（2）=B（s）dB（s）dP（1）P（2）（11）

扩展后的拉格朗日乘子U包含邻接子区域间节点的界面约束λd以及与更新子区域新增节点间的约束η：

U=λdη（12）

基于修正后的布尔矩阵B（s），非线性整体有限元撕裂对接法方程（2）和方程（3）可以改写为

A（s）kδu（s）k+1+B（s）TδUk+1=f（s）ext-B（s）TUk-f（s）int，k（u（s）k）（13）

Nss=1B（s）u（s）k+Nss=1B（s）δu（s）k+1=0（14）

1.3 非线性子区域误判修正

为防止出现某个非线性子区域的误判，在加载步t+1迭代收敛后，每个子区域Ω（s）的非局部等效应变预测值ε（s），peq和非局部等效应变计算值ε（s），maxeq都将与损伤发生的非局部等效应变阈值k（s）0进行对比分析：

Δε（s），peq，t+1=ε（s），peq-k（s）0（15）

Δε（s）eq，t+1=ε（s），maxeq-k（s）0（16）

一旦出现Δε（s），peq，t+1<0且Δε（s）eq，t+1≥0的情况，则表明子区域Ω（s）的非线性出现误判，此时应该将子区域Ω（s）判定为非线性子区域，再返回上一个加载步t进行重新迭代计算，以修正加载步t+1的求解。

2 L型混凝土试件损伤分析的数值试验

2.1 Total-FETI模型及计算参数

为分析子区域分解方式对模型计算结果和计算效率的影响，对图1所示的三维L型混凝土试件采用3种不同的子区域分解方式进行计算对比。试件几何尺寸如图1所示，边界条件为在x=100 mm的R面上施加约束，ux=0 mm和uz=0 mm;在y=0 mm的B面上施加约束uy=0 mm和uz=0 mm;在y=100 mm的顶面施加ux=-0.6 mm和uz=-0.6 mm的位移约束。计算采用隐式梯度损伤模型，其参数说明如下：采用修正的von Mises模型计算等效应变，其混凝土的压缩和拉伸强度比值η为10;采用Mazars模型[24]中的损伤演化法则，其控制软化速率的β取值为50，控制残余应力的α取值为0.999，损伤发生时的应变阈值k0取值为0.000 5;弹性模量E取值为40 000 MPa，泊松比υ为0.2，梯度参数c=1 mm2。将各个子区域的刚度方程和描述各子区域界面和边界条件的布尔矩阵直接组装成有限元支配方程的整体系数矩阵。线性方程组系统采用直接求解法进行求解，求解器为并行直接求解器Pardiso[25]。同时，采用1.3节所述非线性子区域误判修正对每个加载步非线性判断进行复核。

多尺度计算采用粗网格和细网格两套有限元模型，其中细网格模型是在粗网格模型上进行细分得到，如图2所示，均采用八节点六面体单元进行网格剖分。粗网格模型图2（a）的节点总数为3 000，单元总数1 536;细网格模型图2（b）节点总数117 912，单元总数98 304。

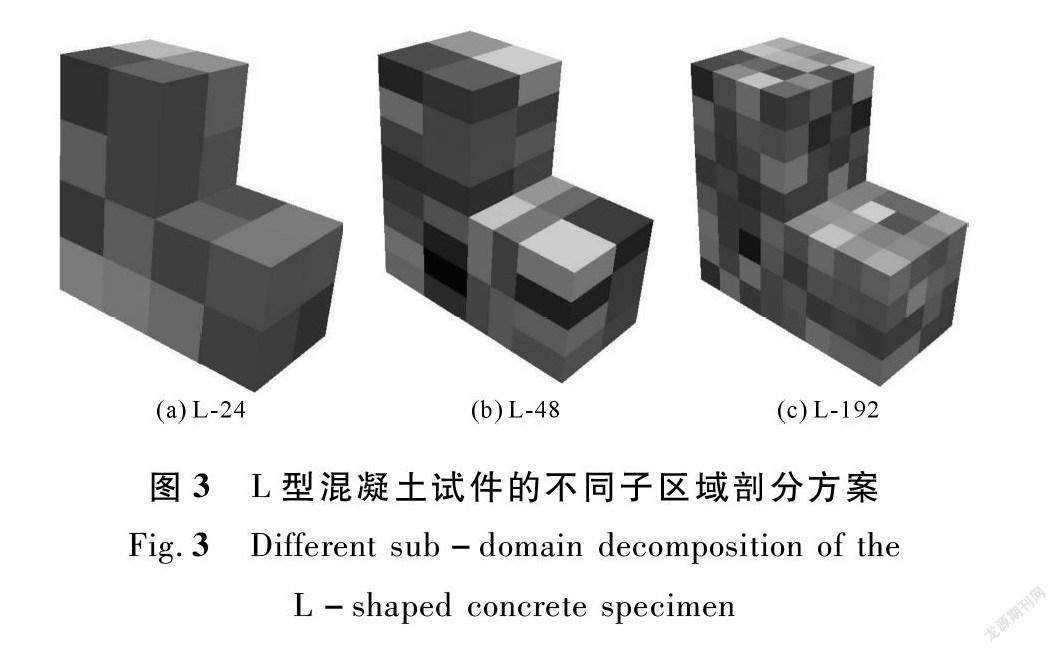
为对比三维情况下不同子区域剖分方式对子区域自适应更新、计算内存和计算时间的影响，将L型混凝土试件分别分解为如图3所示的24个正方体子区域试件，48个长方体子区域试件以及192个正方体子区域试件。需要指出的是，图3（b）所示试件缺口两侧的长方体子区域分别采用水平向布置和竖直向布置，这与其他区域均采用水平布置有所不同。

2.2 试验结果分析

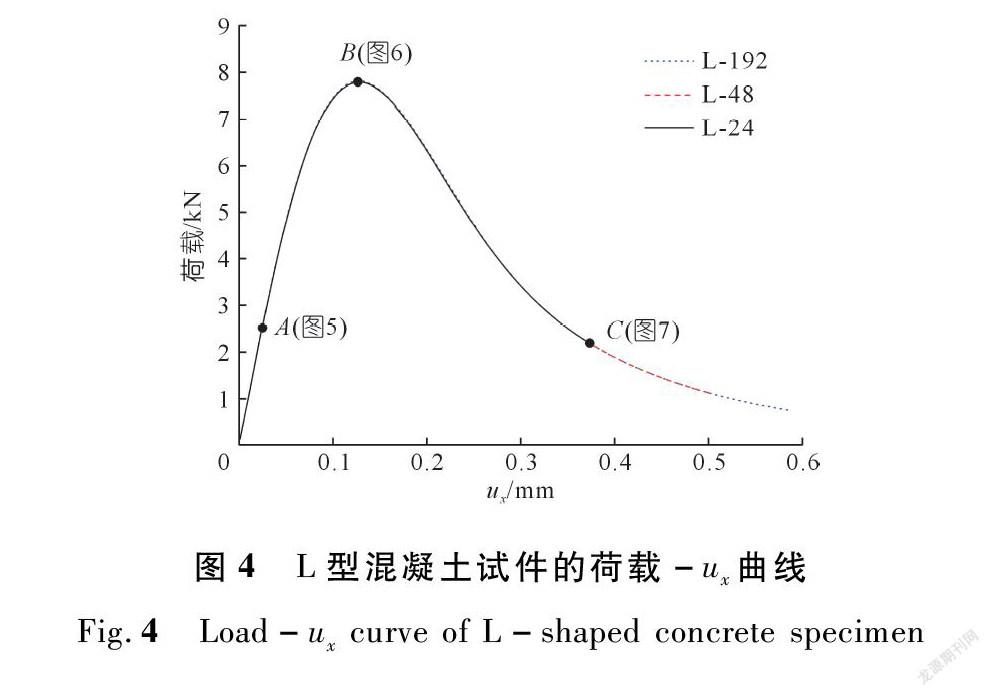
各试件在其y=100 mm试件顶面位置的荷载-ux曲线如图4所示。可以发现，3种不同子区域分解方式下试件的荷载-ux曲线保持基本一致，子区域分解数量增加时，试件刚度呈现微小幅度地增大。接下来，通过选取曲线上的各试件的第一次子区域网格自适应更新的A点、峰值荷载所对应的B点和试件基本完全破坏所对应的C点的各子区域网格自适应更新情况进行对比分析。

如图5所示，3个试件的第一次基于子区域的自适应网格更新数量不一样。直观来看在这个阶段呈现的规律是子区域分解数量越多，则自适应更新的网格数量越少。定量分析表明：其中该阶段L-24的网格总数为13 632，为全局细观网格总数的13.87%，内存占用量2 286 MB;L-48的网格总数为7 584，为全局细观网格总数的7.71%，内存占用量1 542 MB;L-192的网格总数为3 048，为全局细观网格总数的3.10%，内存占用量1 785 MB。定量分析结论和直观規律基本一致，但是内存占用量反而是L-192较L-48增大了15.8%，可见在此阶段大幅增加子区域分解数量会使得界面自由度加大，削减了其减少自适应网格更新数量带来的效率。

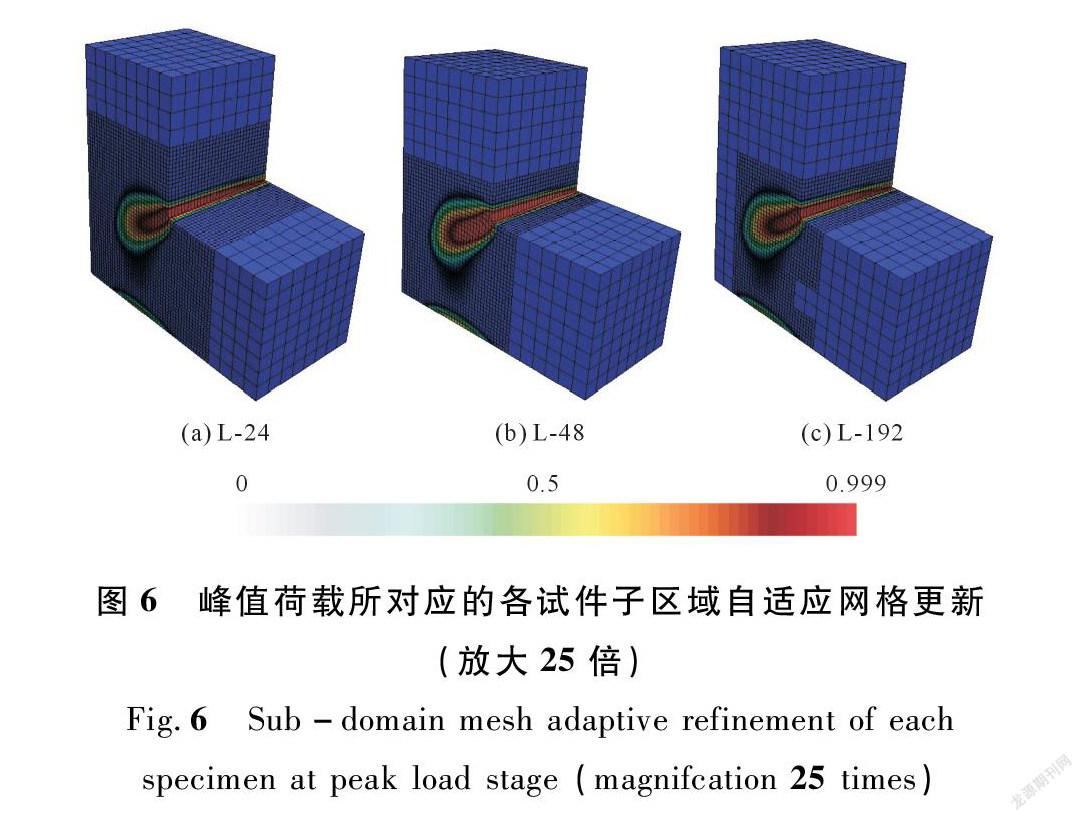
如圖6所示为3个不同子区域剖分形式试件在峰值荷载阶段的自适应网格更新数量。直观来看仍是随子区域分解数量加大自适应更新的网格数量减少。定量分析表明：该阶段L-24的网格总数为45 888，为全局细观网格总数的46.68%，内存占用量7 358 MB;L-48的网格总数为33 792，为全局细观网格总数的34.38%，内存占用量5 728 MB;L-192的网格总数为20 184，为全局细观网格总数的20.53%，内存占用量4 607 MB。定量分析结论和直观规律一致，同时内存占用量也呈现随子区域剖分数量增加而递减的情况，说明子区域界面自由度增加所导致的计算效率下降影响在子区域数量更新中期已经不再明显。

如图7所示，3个不同子区域分解形式试件在基本完全损伤阶段的自适应网格更新总数量与前述阶段的规律一致，即均随子区域数量递增而减少。定量分析表明：L-24的网格总数为57 984，为全局细观网格总数的58.98%，内存占用量9 271 MB;L-48的网格总数为43 872，为全局细观网格总数的44.63%，内存占用量7 338 MB;L-192的网格总数为34 800，为全局细观网格总数的35.40%，内存占用量7 014 MB。定量分析结论和直观规律一致，子区域分解数量的增加可明显减小计算网格模型规模以及内存使用量，子区域界面自由度增加对计算效率降低的影响较小。同时，图7（b）可解释为何将L-48试件缺口两侧子区域分别设置为水平向和竖直向布置，因为本文自适应网格更新是基于子区域网格更新进行的，根据损伤可能的扩展形式将两侧子区域设置为不同方向可使得损伤影响的子区域尽量少。再从计算时间来看，L-24计算时间为13.79 h，L-48计算时间为10.68 h，L-192计算时间为8.72 h。可知L-48和L-192的计算时间相差较小，进一步说明了合理划分子区域形式也是提高计算效率的有效手段。

综上可知，不同子区域分解方式的损伤扩展模式以及荷载-ux曲线均保持良好的一致性，子区域的不同形式以及不同数量的分解对计算结果影响不大，模型不存在子区域分解敏感性。对比分析不同子区域分解数量的网格更新结果和计算内存需求可知，子区域网格分解数量越多所需要的计算网格数量越小，计算所需内存也呈现同样规律，且此优势在子区域自适应更新的中后期更为明显。因为从网格增长速率来看，L-24和L-48网格在后期增长较慢，说明自适应更新中期精细网格已经基本上被替换，整体计算效率要自然比L-192网格更新随损伤发展均匀替换要低。

3 结 论

本文采用隐式梯度损伤模型作为混凝土损伤分析的本构模型，并采用Total-FETI方法进行混凝土损伤失效过程的自适应并发多尺度区域分解模拟。针对混凝土损伤子区域的高精度模拟要求和损伤扩展路径的不确定性问题，通过L型混凝土试件数值试验开展了子区域分解对模型规模及计算效率的影响研究，主要得出以下结论。

（1） 对混凝土试件采用不同的子区域分解形式和分解数量进行对比分析，计算所得损伤模式一致，可知模型无区域分解敏感性。

（2） 由于模型各子区域均采用粗网格，仅局部非线性子区域进行高精度细观网格替换，界面节点数量增加对计算规模和计算效率影响较小。

（3） 子区域数量分解越多，自适应更新的高精度子区域越少，有限元模型网格数量减少，从而计算效率提高。

（4） 子区域分解方式与损伤可能扩展路径相适应，损伤区域涉及的高精度子区域越少，模型耗费计算资源削减，计算效率改进。

综上可知，子区域分解方式和子区域分解数量对自适应网格更新总数及计算所需内存影响显著，合理的子区域剖分方式和适当的子区域分解数量可以有效降低计算规模和计算内存需求。

参考文献：

[1] 吴佰建，李兆霞，汤可可.大型土木结构多尺度模拟与损伤分析：从材料多尺度力学到结构多尺度力学[J].力学进展，2007，37（3）：321-336.

[2] 胡少伟，陆俊，范向前.混凝土损伤断裂性能试验研究进展[J].水利学报，2014，45（增1）：10-18.

[3] 林皋，刘军，胡志强.混凝土损伤类本构关系研究现状与进展[J].大连理工大学学报，2010，50（6）：1055-1064.

[4] 张立，李广凯，马怀发.混凝土类材料弹塑性损伤问题的全隐式迭代法[J].水利学报，2020，51（8）：947-956.

[5] 汪忠明，牛晓玉，杨伯源.基于隐式梯度公式的各向异性混凝土损伤研究[J].工程力学，2011，28（2）：159-164.

[6] 任宇东，陈建兵.基于一类非局部宏-微观损伤模型的混凝土典型试件力学行为模拟[J].力学学报，2021，53（4）：1196-1211.

[7] 肖诗云，朱梁.混凝土初始损伤细观结构特性数值试验研究[J].大连理工大学学报，2017，57（1）：78-86.

[8] 徐青，周祥森，程志诚.基于Ansys的混凝土随机骨料模型及细观力学分析[J].武汉大学学报（工学版），2019，52（12）：1035-1040，1047.

[9] 王康，吴佰建，李兆霞.损伤跨尺度演化导致的混凝土强度尺寸效应[J].东南大学学报（自然科学版），2014，44（6）：1230-1234.

[10] 程道辉，王苗，卿龙邦，等.混凝土Ⅰ型裂缝随机损伤断裂分析研究[J].混凝土，2020（11）：40-42，56.

[11] PEERLINGS R R.Enhanced damage modelling for fracture and fatigue[D].Eindhoven：Technische Universiteit Eindhoven，1999.

[12] SIMONE A，WELLS G N，SLUYS L J.From continuous to discontinuous failure in a gradient-enhanced continuum damage model[J].Computer Methods in Applied Mechanics and Engineering，2003，192（41-42）：4581-4607.

[13] 汪忠明，牛曉玉，杨伯源.基于非局部隐式梯度模型的混凝土断裂损伤[J].中国科学技术大学学报，2010，40（6）：651-656.

[14] 汪忠明.基于非局部增强梯度模型的混凝土断裂损伤研究[D].合肥：合肥工业大学，2010.

[15] FARHAT C，ROUX F X.A method of finite element tearing and interconnecting and its parallel solution algorithm[J].International Journal for Numerical Methods in Engineering，1991，32（6）：1205-1227.

[16] 张云鹏，杨新生，邵定国，等.基于自适应区域分解的电磁场有限元求解方法研究[J/OL].高电压技术.https：∥doi.org/10.133361/j.1003-6520.hev.20201807.

[17] 张晓虎，孙秦.结构非匹配网格区域分裂的并行数值计算研究[J].西北工业大学学报，2019，37（4）：650-655.

[18] DOSTL Z，HORK D，KUERA R.Total FETI—an easier implementable variant of the FETI method for numerical solution of elliptic PDE[J].International Journal for Numerical Methods in Biomedical Engineering，2006，22（12）：1155-1162.

[19] ERMK M，HAPLA V，HORK D，et al.Total-FETI domain decomposition method for solution of elasto-plastic problems[J].Advances in Engineering Software，2015，84.

[20] LLOBERAS-VALLS O，RIXEN D J，SIMONE A，et al.Domain decomposition techniques for the efficient modeling of brittle heterogeneous materials[J].Computer Methods in Applied Mechanics and Engineering，2011，200（13-16）：1577-1590.

[21] LLOBERAS-VALLS O，RIXEN D J，SIMONE A，et al.Multiscale domain decomposition analysis of quasi-brittle heterogeneous materials[J].International Journal for Numerical Methods in Engineering，2012，89（11）：1337-1366.

[22] HAIKAL G，HJELMSTAD K D.An enriched discontinuous Galerkin formulation for the coupling of non-conforming meshes[J].Finite Elements in Analysis & Design，2009，46（6）：496-503.

[23] LLOBERAS-VALLS O，RIXEN D J，SIMONE A，et al.On micro-to-macro connections in domain decomposition multiscale methods[J].Computer Methods in Applied Mechanics and Engineering，2012，225-228：177-196.

[24] 柯杨，姜胜涛，李佳，等.不同骨料体积率的轻混凝土损伤-断裂分析[J].混凝土，2020（7）：15-19，24.

[25] 曹大志，强洪夫，任革学.基于OpenMP和Pardiso的柔性多体系统动力学并行计算[J].清华大学学报（自然科学版），2012，52（11）：1643-1649.

（编辑：郑 毅）

Research on sub-domain meshing of concrete damage analysis based on Total-FETI method

QIU Liting，MA Fuheng，SHEN Xinzhe

（Nanjing Hydraulic Research Institute，Nanjing 210029，China）

Abstract：

Based on combination of total finite element tearing-interconnecting method and gradient-enhanced continuum damage model，aiming at the high-precision requirements of the damage sub-domain simulation and the uncertainty of concrete damage propagation path，through introducing the sub-domain adaptive updating method based on non-local equivalent strain，and incorporating the sub-domain update misjudgment correction，the high-precision finite element mesh adaptive update of nonlinear sub-domain during concrete damage and failure process simulation were realized.Moreover，numerical tests having different domain meshing numbers and domain meshing forms were carried out on L-shaped concrete specimen.The results show that there was no sub-domain meshing sensitivity for the model.When the number of sub-domain subdivision increased or the meshing mode of sub-regions was adapted to the damage propagation path，the number of adaptive updating of the sub-domain with high-precision finite element mesh decreased，and the calculation scale of the model was significantly reduced.In addition，the increment of sub-regional interface nodes had little effect on the reduction of calculation scale，and the overall calculation efficiency of the model was significantly improved.This study can provide reference for concurrent multi-scale numerical calculation of concrete damage analysis.

Key words：

concrete damage;gradient-enhanced continuum damage model;total finite element tearing-interconnecting method;sub-domain adaptive updating;sub-domain decomposition pattern;computational efficiency