挂治电厂2号机在线监测振摆数据降噪处理方法
2022-05-21杨峰雄付向涛袁翔
杨峰雄,付向涛,袁翔
(五凌电力有限公司挂治电厂,湖南 长沙 410000)
近年来,随着大型水轮机组的投运,机组振动问题变得愈发突出,并具有很高的危害性,并可在过流部件中传播、引发共振、大轴摆动、并降低水轮机组某些部件的使用寿命等,甚至可能引起厂房振动。因此,对运行机组振摆进行实时监测是确保机组安全运行的重要手段[1-5]。水轮机组的在线监测由于水电机组的结构复杂,水轮机组的故障机理尚不明确,而且运行中的水轮机组的振动大多由于水力、电磁、机械以及环境噪声等因素耦合叠加的结果。直观的数据判断和简单的分析很难找到振动具体原因。为了为更好保证系统监测数据的真实性以及后续信号特征分析的有效性,发掘更多有用信息,在分析数据之前需要对信号进行降噪处理[6-9]。
目前很多国内外的学者对旋转机械信号处理进行了研究并取得了很大的进展。
文献[10-12]采用小波阈值方法对齿轮超声信号进行降噪处理,其在一定程度上可以对信号进行降噪,但传统的小波阈值降噪等方法不能自适应的对信号进行降噪处理,同时在处理这类非线性非平稳性信号时存在小波基和分解层数选择上的局限性。文献[13]采用VMD进行水电机组故障信息提取,但VMD分解本身不具备自适应分解能力,需要进行分解层数的设定。文献[14]提出基于EMD水轮机空化声发射信号特征提取方法研究,该方法将EMD用于水轮机空化非平稳信号处理中,将关联维数作为水轮机空化的特征,其表征的特征明显,这表明EMD可以用于非平稳信号的处理。
水轮机组振动信号具有明显的非线性、非平稳性特征,在进行特征提取过程中,受电磁环境等噪声干扰,其故障特征不明显。因此,在小波阈值降噪方法的基础上,结合EMD算法的自适应性特征,不需要事先确定基函数和分解层数,整个分解过程完全是由信号自身决定。从而有效地克服了小波降噪的固有缺陷,目前该方法已被应用于非平稳信号的降噪处理。
本文提出一种基于EMD与小波阈值相结合的降噪方法,对实际信号有很强自适应处理能力以及较高的信噪比,并与小波阈值降噪方法进行了比较。
1 基于EMD与小波阈值降噪处理方法
1.1 EMD分解方法
EMD算法是近年来发展起来的一种新型自适应性视频分析算法[15-17],它依据信号自身特点,自主选取信号内在的本征固有模态函数,是一种适用于处理非平稳、非线性信号的算法。该方法是对以线性和平稳假设为基础的傅里叶分析和小波变换等相关传统时频算法的重大突破。频率是建立在以傅里叶变换为基础与时间无关的物理量,其实质是信号在一段时间以内的总体特征,这种方法对于平稳线性信号的分析是有效的。但是,在工程实际中,对于非平稳信号,其频率是随时间变化的,传统方法就不再适用。EMD就是将原有信号分解为许多窄带分量,这种理念的本质就是通过非线性,非平稳信号的分解获得一系列表征信号特征时间尺度的IMF,将非平稳非线性信号分解为许多平稳信号。信号分解过程中,每个IMF需要满足2个条件[18-20]:①在整个数据序列中极值点数量与过零点的数量相等或者相差一个;②在任何时间点上,由局部极大值和极小值所构成的包络均值为0。IMF函数的求取步骤如下:
(1)首先,找到原信号X(t)所有极大值点,通过三次样条插值你和出极大值点的包络线e1,同理,找到原信号X(t)所有极小值点,用三次样条插值拟合原数据序列的极小值包络线e2,求出包络均值m1。
(1)
(2)用原数据序列x(t)减去m1后得到一个去掉低频的新数据h1:
x(t)-m1=h1
(2)
(3)判断h1是否满足IMF函数的两个条件,若满足,则h1为第一个IMF函数,把它赋给c1。若不满足条件,则把h1当作原序列,重复上述步骤k次,直到找到第一个IMF函数。
(4)当原始数据x(t)减去第一个c1得到一个去掉高频成分的剩余序列r1。
r1=x(t)-c1
(3)
(5)当r1被当做原始序列重复上述步骤,找出c2,如此循环j次,直到rj小于给定误差或者趋于单调函数的时候停止。
最终信号x(t)经过EMD处理后可以表示为:
(4)
1.2 小波阈值降噪
小波变换的一个重要应用之一就是信号降噪。
对信号降噪的本质是通过抑制信号中的无用信息,增强信号中有用信息的过程[21-22]。
采用标准的正交小波基,建立一个N*N的正交矩阵W,然后进行离散小波变换(the discrete wavelet transform,DWT):
C=WX
(5)
其中,X=[X(1),X(2),X(3),……,X(N)],C=[C(1),C(2),C(3),……,C(N)],以及重构的小波系数。
小波阈值降噪的思想就是对小波分解后的各层系数中模大于和小与某一阈值的相关系数进行处理,然后对处理过后的小波系数进行反变换,重构出降噪后的信号[23-25]。其阈值计算方式为:T=VC,其中C为常数。常用阈值函数主要有硬阈值函数和软阈值函数,其函数定义如下:
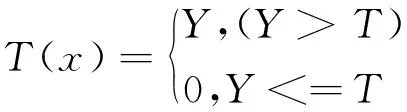
(6)
和
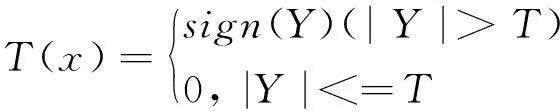
(7)
通常情况下软阈值法较硬阈值法能更好地保留信号的有用信息,所以多用于对工程信号的降噪。本文采用软阈值函数,得到的降噪信号的估计值为:
(8)
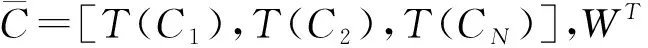
在最小最大估计值的限制下得出的最优阈值为:
(9)
其中δ是噪声标准方差,N是信号长度,根据上式得到信号噪声的标准差估计值,即:
(10)
降噪的效果采用信噪比SNR和均方根误差(RMSE)进行衡量,SNR的定义为:
(11)
均方根误差(RMSE)定义为:
(12)
1.3 EMD与小波阈值降噪处理方法
EMD分解后噪声模态分量主要集中在前3阶IMF中,直接利用小波(包)阈值降噪难以摆脱基函数和分解层数选取对降噪效果的影响。若对其进行传统EMD降噪,将EMD分解后的含噪低阶IMF机械地剔除,然后再对剩余IMF进行重构,能达到一定的降噪效果,但会导致部分真实信号的缺失,造成降噪的失真,对后期的信号特征提取工作产生不利影响。另外,采集信号由于受设备稳定性及环境干扰的影响易产生偏离基线。偏离基线的大小随时间变化而变化,会在采集的信号频域内产生附加的低频成分。若采集信号存在偏离基线,则产生的趋势项必然存在于EMD分解的残余项rn中[26-27]。
因此,根据EMD自适应分解特性和阈值降噪的良好性能优点,本文建立了基于EMD与小波阈值降噪方法。其流程图如图1所示。

图1 降噪算法的流程图Fig.1 Flow chart of noise reduction algorithm
具体方法具体实现步骤如下:
(1)将采集的空化声发射信号X(t)进行EMD分解,得到一系列IMFi(i=1,2,…,n)和残余量rn。
(2)根据噪声信号在IMF中的分布特性,对EMD分解得到的前3个IMF分量(进行阈值降噪处理,得到IMFi′(i=1,2,3)。
(13)
(3)剔除残余量rn,以消除残余分量的影响。鉴于残余分量的存在,本文采用一种基于能量谱的模态识别方法该方法的具体方法如下,在EMD分解完成的基础上,计算IMF的能量:
E(Xi)=X(t)2
(14)
式中:X(i)为第i个IMF分量。对每一个IMF分量进行归一化处理:
(15)
计算IMF的能量谱:
e=-Pi*lg[Pi]
(16)
将变量取对数后不仅与数值大小的单调性相关,同时还与事件发生的概率相关。残余IMF的e较小。本文取残余IMF分量的阈值为0.1,当IMF的能量谱e小于0.1的时候,就可以认为该IMF分量为残余模态分量。
(4)对处理后的IMFi′(i=1,2,3)以及未处理的IMFi(i=(4,5,…,n)进行信号重构,得到降噪后信号Y(t),即:
(17)
EMD与小波阈值降噪方法的优点包括:①具备EMD的自适应性、多分辨率、完备性等优势;②确保噪声起主导作用并且含有用信息的IMF分量不被剔除;③避免了小波最优分解层数的选择,同时也避免了小波分解过程中小波基函数选择的烦琐性,从而更容易对振摆非平稳信号进行降噪处理[28]。
1.4 仿真信号处理
采用EMD与小波阈值降噪方法对设置SNR为5dB,长度2048个点的Doppler原始仿真加噪信号进行降噪处理。
其原始仿真信号、仿真加造信号、仿真降噪信号如图2-图5所示。
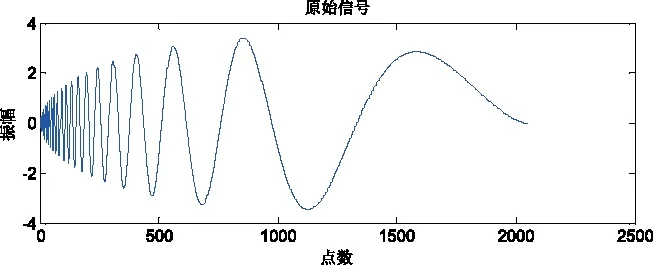
图2 仿真信号Fig.2 Simulation signals
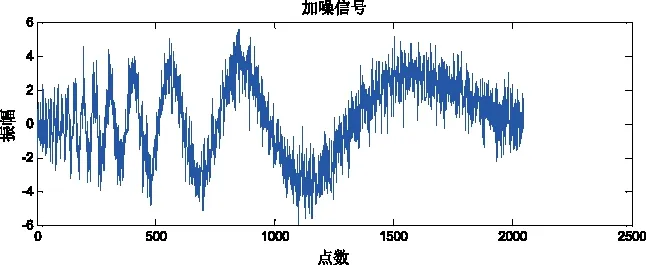
图3 加噪信号Fig.3 Noise signals
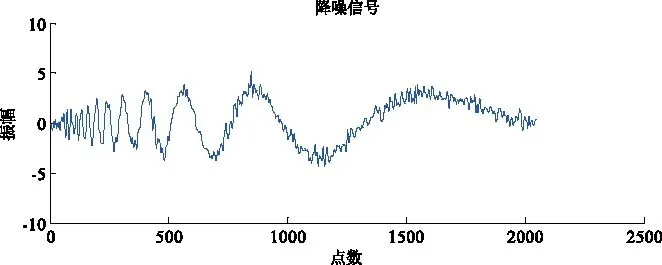
图4 EMD与小波阈值降噪信号Fig.4 EMD and wavelet threshold denoising signals
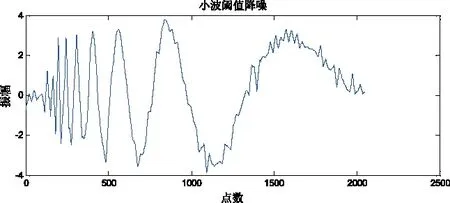
图5 小波阈值降噪信号Fig.5 Wavelet threshold denoising signals
对含噪仿真信号X(t)分别用EMD与小波阈值降噪方法、并与传统小波阈值降噪方法进行对比,其中选取db4小波为基函数,分解层数为四层,结果如图5所示。对比图4和图5的2种方法降噪后信号的波形图可以看出,2种降噪方法处理后信号的波形轮廓基本与原信号一致。对比发现,小波阈值降噪降噪效果明显差于本文的降噪方法,图4波形图较小波阈降噪方法所得波形更为平滑,且波形轮廓更接近原信号。同时图5小波降噪的波形存在一定程度的失真,是过度降噪的表现。为进一步对比小波降噪和EMD与小波降噪2种降噪手段的优劣性,采用信噪比(SNR)和均方根误差(RMSE)作为其降噪效果好坏的评价指标。2种降噪方法的SNR对比结果如表1所示。
由表1可知,两种方法降噪后的信号信噪比都比含噪仿真信号高,说明2种方法均具有一定的降噪作用。特别需要指出的是:经 EMD与小波阈值降噪方法降噪后信号的信噪比更高,说明该方法相比较传统小波阈值降噪效果更好。同时,从均方根误差来看,本文提出的EMD与小波阈值降噪的均方根误差更小,降噪的实际效果更明显。
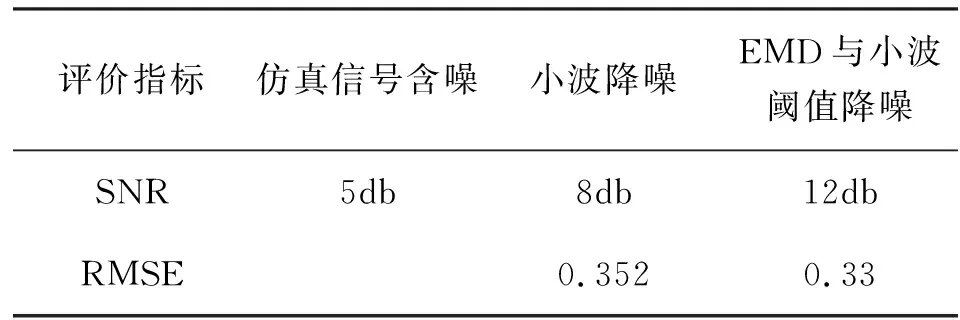
表1 两种方法降噪效果对比Tab.1 Comparison of 2 signal denoising methods
2 在线监测系统振摆系统与试验数据采集和降噪处理
2.1 在线监测系统介绍
PSTA2100水轮发电机组在线状态监测和分析系统,如图6所示。水轮机在线监测系统提供对机组当前的运行状态进行同步监视和显示的功能,以数值、曲线、图表等各种形式,将机组的各种状态分析数据,通过多个不同的页面展现给电站运行维护人员。实时监测系统同时会将各通道的报警状态在监测终端同步显示,电站运行维护人员可以根据这些状态判定是否需要检修维护人员参与机组检查调整。本系统提供专业数值分析工具可对历史数据进行详尽专业的分析,通过选取相关的监测量可以查看这些监测量的实时值,实时评价以及通过检索服务器的数据到本地还可以对离线数据进行趋势分析和关联分析。在水电行业使用还可以利用它进行专业分析,其具有如下特点:

图6 在线监测系统Fig.6 Online monitoring systems
(1)全组态化配置界面,支持用户自定义展示界面。
(2)Web展示模式,支持客户端和移动端使用。
(3)内嵌丰富专业图形组件,支持水电专业应用界面配置。
(4)插件化封装,支持图形控件扩展。实时数据评价。
(5)形成实时评价报告:针对机组运行过程中的实时数据进行ABCD四级实时评价,以得出各测点数据的优秀、合格、危险、严重状态,反应机组当前运行情况。
(6)形成定时评价报告。可根据用户设定的时间在固定的时间点输出评价报告,报告内容可根据用户需求进行定义,包括常规的振摆峰峰值、气隙最小值,本系统特有的振摆分频值,以及各种计算量,例如转子不度、转子质量不平衡量等。
(7)形成条件评价报告。用户可设定在机组某种运行工况下输出评价报告,例如开机低转速,空转、空载、加励磁、某个负荷、停机、跳机等等所有机组可能的运行工况。
(8)形成趋势检查报告。定期绘制用户设定监测量的时间轴趋势,以方便用户对机组运行状态是否劣化,进行直观评价。
(9)形成报警统计报告。机组运行数据报警统计,用户可根据统计数据验证报警参数设置是否合理,机组是否有误报、漏报现象,在确认报警都是合理一情况下检查报警数据有针对性的修复机组缺陷使数据恢复正常。水轮机组状态在线监测系统具有运行状态评价功能,系统采用量化评价技术,评价内容包括界面或系统软件工具以原有的波形、点值自动计算生成的计算量,只要是对运行检修维护指导和评价工作有实用意义的,都可以归入运行状态评价报告。
其中,用于数据采集的SPU2010数据采集箱能同时稳定可靠进行大量数据预处理计算、网络数据传输。数据采集箱对各种不同测量信号系统设有多种信号调理模块,以便于适应不同种类的传感器信号(如电压、电流、压力),同时具有热插拔以及易于更换等特点。采集箱采样频率范围为0Hz~500Hz,确保数据的实时性、准确性、连续性和可靠性。
每台机组在线监测系统共使用4支申克电涡流式的摆度传感器(位移传感器),8支豪瑞斯振动传感器(速度传感器)。电涡流式摆度传感器用于静态和动态位移量的非接触式测量,测量动轴承位移量和记录位移轨迹。振动传感器由地震块和弹簧片支持的测量线圈组成,测量元件可在圆形永久磁铁的磁场中移动,传感器的振动会产生一个与振动速度成正比的电压信号。
其中,机组下导和水导摆度传感器分别位于下导和水导油盆上方,用支架支撑,在机组水平面+X、+Y方向各安装一个传感器(从上往下俯瞰机组,垂直于上游侧为+X方向,平行于上游侧为+Y方向)。机组的下机架+X、+Y和下机架垂直方向,顶盖的+X、+Y和顶盖垂直方向各安装一只振动传感器,定子基座+X、+Y方向分别安装一只振动传感器,用以采集机组振动的数据。
其基本原理为:前端元器件实现数据实时采集,线号经端子箱转接后送至下位机柜内SPU2100数据采集单元进行AD转换;多个数据采集单元处理后的数据经交换机汇聚在工业平板电脑集中存储、展示;平板电脑与电站计算机监控系统机组LCU 之间可通过MODBUS协议实现实时通信;多台机机组的数据通过光纤设备汇聚到上位机服务器上,上位机服务器对数据进行集中处理、存储、分析;二区服务器和三区服务器之间用正向隔离设备进行隔离,数据实现同步备份,维护人员只对三区服务器进行操作。
2.2 试验数据采集和降噪处理
本文从2号机变负荷工况下,截取其中一段摆度数据,如图7所示。

图7 变工况下摆度信号Fig.7 Swing signals under off design condition
从图7可以看到:采集信号波形不平整光滑,波峰、波谷含有大量毛刺,这是由工作环境背景噪声、电磁干扰、其他机械故障引发的冲击噪声叠加而造成的。由于噪声信息的干扰将加大对采集振摆信号进行分析处理的难度,从而,需要对采集的振摆信号进行降噪处理,以方便其后续的分析研究。
从图8可以看到:基于EMD与小波阈值的降噪方法对振摆的噪声成分有一定的抑制作用。采集信号波形图上明显的毛刺部分已被很好地抑制,这对信号的后期数据分析、处理是有利的。相比原始振摆采集信号,降噪后的信号更平滑,且很好地保留了原信号的突变特征和振幅。

图8 降噪信号Fig.8 Noise reduction signals
对比图9、图10的频谱图,发现降噪后的信号频谱基本上保留了原始信号中频谱的主要部分,对50Hz以上的高频噪声信号成分进行了很好地抑制,这验证了该降噪算法的可行性。
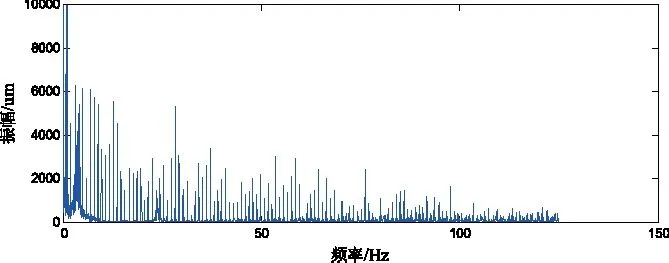
图9 原始信号频谱图Fig.9 Spectrum of original signals

图10 降噪信号频谱图Fig.10 Spectrum of noise reduction signals
3 结论
EMD与小波阈值降噪方法有效结合了EMD自适应性和小波阈值降噪的优点,极大地克服了传统小波阈值降噪方法的机械性缺陷和小波基函数与分解层数选取的局限性,整个分解过程是由信号自身特性决定的自适应降噪过程。
本文提出的EMD与小波阈值降噪方法适用于水轮机振动信号的降噪处理这一领域,仿真试验结果表明该方法相较于传统小波阈值降噪方法更有优势。
实际工况下的振摆数据降噪结果表明,该方法对振摆数据中的噪声有良好的抑制作用,这表明这种基于EMD与小波阈值降噪相结合的方法对于水轮机振摆数据的降噪是有效的。
