中国31个主要城市空气质量的聚类分析和主成分分析
2022-05-20孟彦菊
虞 颖, 孟彦菊
(云南财经大学 统计与数学学院, 昆明 650221)
空气是人类赖以生存的最基本的环境要素之一。近几年来,经济和科技迅速发展,城镇化进程加快,人民生活水平得到了提高[1]。在社会面貌发生可喜变化的同时,空气污染程度越来越严重,空气质量问题在生态领域显得比较突出。空气污染会产生雾霾和酸雨,直接或间接威胁人类的健康,更会影响生态自然的和谐与可持续发展[2]。绿水青山就是金山银山,发展经济不应只局限于眼前的得利,也要考虑到子孙后代的生存与发展,因此要走绿色发展的道路,在发展的同时保护好生态环境。
空气污染与经济发展有着密切的联系,治理空气污染对于经济发展有好处,是生态可持续发展的必经之路[3-4]。空气质量的好坏反映了空气污染的程度,研究空气质量、改善空气质量不仅有利于更好地发展经济,而且对于人类的生命健康和生态自然保护有着重要的意义。同时为国家和政府制定相关改善空气质量的政策提供参考[5]。
1 研究方法
聚类分析就是将研究对象(样品或变量)按照各自特性进行合理分类的一种多元统计方法。目前聚类分析已广泛应用于经济、管理、医学、心理学、气象预报、地质勘探、生物分类等诸多领域。本文基于全国31个主要城市空气质量数据进行K均值聚类[6]。
主成分分析也称主分量分析,是由Hotelling于1933年提出的一种常用的多元统计方法。基本思想是用个数较少,但是保留了原始变量大部分信息的几个不相关的综合变量(即主成分)来代替原来较多的变量,从而可以简化数据,对原来复杂的数据关系进行简明有效的统计分析[7-9]。
2 城市空气质量聚类分析
2.1 数据说明
本文使用的数据是全国31个主要城市空气质量的数据,来源于PM2.5历史数据网站,包含月份、AQI、范围、质量等级、PM2.5、PM10、SO2、CO、NO2、O3和城市这些指标,数据时间跨度为2013年12月至2021年4月。
2.2 数据处理
基于收集到的数据,选取月份、质量等级、PM2.5、PM10、SO2、CO、NO2、O3和城市这些指标,分别计算各个城市PM2.5、PM10、SO2、CO、NO2、O3的月平均浓度,根据质量等级计算质量等级优和良的天数,得到新的数据表,见表1。
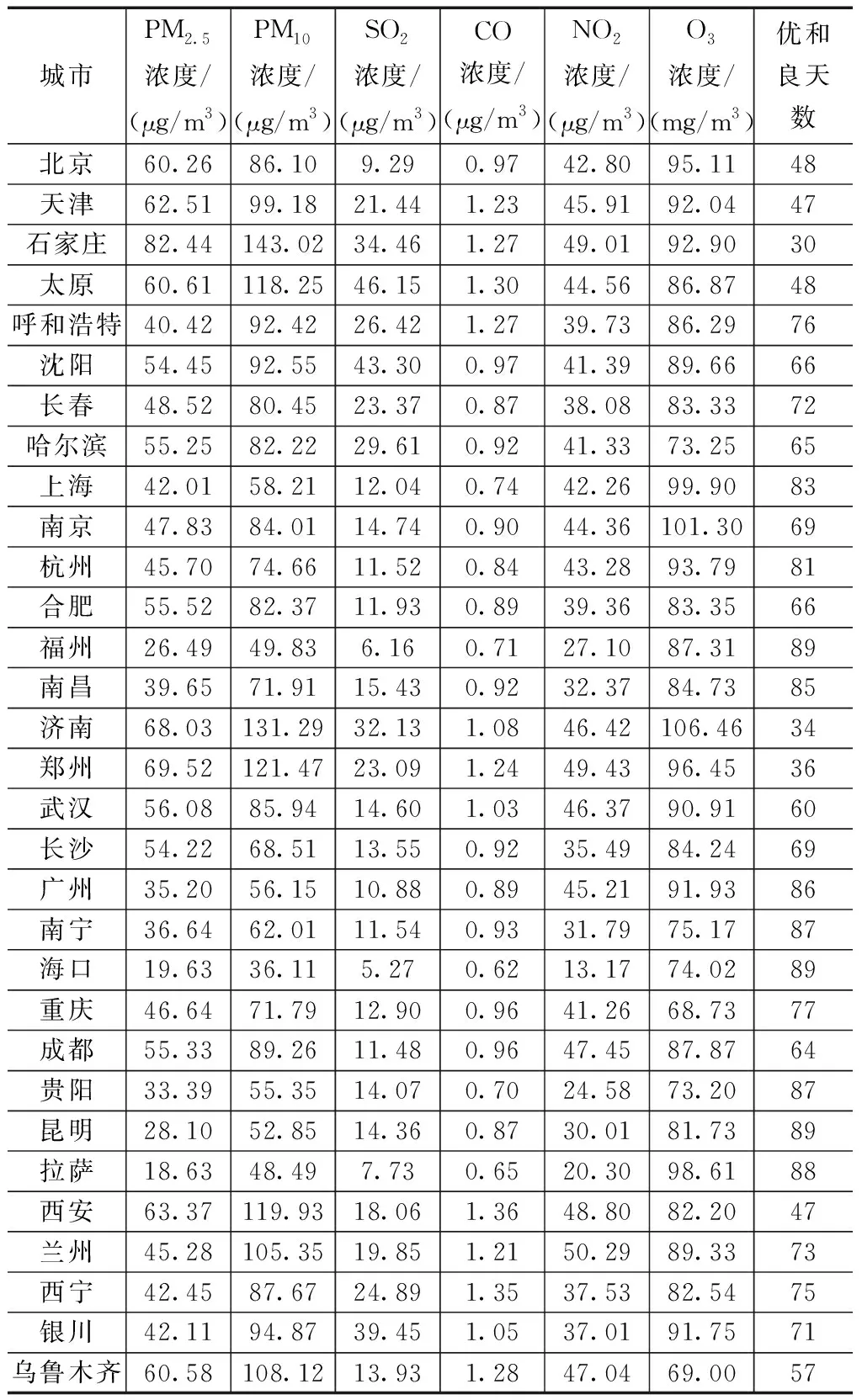
表1 全国31个主要城市空气质量数据
后面进行的聚类分析和主成分分析都是基于数据处理之后得到的。
2.3 系统聚类和K均值聚类
用R软件对全国31个主要城市空气质量进行聚类分析[10]。先采用类平均法做系统聚类,分别绘制合并距离为38和35的两条水平线。
如果取合并距离为38,则31个城市可分为4类。
第1类:西安、乌鲁木齐。
第2类:太原、石家庄、济南、郑州。
第3类:南京、合肥、武汉、成都、北京、天津、兰州、沈阳、银川、哈尔滨、长春、呼和浩特、西宁。
第4类:长沙、重庆、上海、广州、杭州、南昌、海口、拉萨、南宁、贵阳、福州、昆明。
如果取合并距离为35,则31个城市可分为5类。
第1类:西安、乌鲁木齐。
第2类:太原、石家庄、济南、郑州。
第3类:南京、合肥、武汉、成都、北京、天津、兰州、沈阳、银川、哈尔滨、长春、呼和浩特、西宁。
第4类:长沙、重庆、上海、广州、杭州、南昌。
第5类:海口、拉萨、南宁、贵阳、福州、昆明。
系统聚类结果如图1所示。

图1 系统聚类结果
系统聚类两种情形下除长沙、重庆、上海、广州、杭州、南昌、海口、拉萨、南宁、贵阳、福州、昆明这几个城市外,其余城市的分类相同。合并距离38情况下,将这些城市分为一类,合并距离为35情况下,则将这些城市分为两类。
对这31个城市空气质量进行K均值聚类,K取4时聚为4类[11]。
第1类:北京、天津、呼和浩特、沈阳、长春、哈尔滨、南京、合肥、武汉、成都、兰州、西宁、银川、乌鲁木齐。
第2类:上海、杭州、南昌、长沙、广州、南宁、重庆。
第3类:福州、海口、贵阳、昆明、拉萨。
第4类:石家庄、太原、济南、郑州、西安。
聚类结果见表2。

表2 聚类分析K=4聚类结果
K取5时聚5类。
第1类:呼和浩特、沈阳、长春、 哈尔滨、兰州、西宁、银川。
第2类:福州、海口、贵阳、昆明、拉萨。
第3类:北京、天津、南京、合肥、武汉、成都、乌鲁木齐。
第4类:石家庄、太原、济南、郑州、西安。
第5类:上海、杭州、南昌、长沙、广州、南宁、重庆。
聚类结果见表3。

表3 聚类分析K=5聚类结果
K均值聚类两种情形下除北京、天津、呼和浩特、沈阳、长春、哈尔滨、南京、合肥、武汉、成都、兰州、西宁、银川、乌鲁木齐这几个城市外,其余城市的分类相同。K取4情况下,将这些城市分为一类;K取5情况下,则将这些城市分为两类。
2.4 两种聚类分析的比较
系统聚类和K均值分为4类的结果略有不同,系统聚类和K均值分为5类的结果也有差异。
分为4类时,无论在系统聚类或者K均值聚类情况下,太原、石家庄、济南、郑州这4个城市在同一类;南京、合肥、武汉、成都、北京、天津、兰州、沈阳、银川、哈尔滨、长春、呼和浩特、西宁这13个城市在同一类;长沙、上海、广州、杭州、南昌、南宁这6个城市在同一类;重庆、海口、拉萨、贵阳、福州、昆明这6个城市在同一类。
分为5类时,无论在系统聚类或者K均值聚类情况下,太原、石家庄、济南、郑州这4个城市在同一类;南京、合肥、武汉、成都、北京、天津这6个城市在同一类;兰州、沈阳、银川、哈尔滨、长春、呼和浩特、西宁这7个城市在同一类;长沙、重庆、上海、广州、杭州、南昌这6个城市在同一类;海口、拉萨、贵阳、福州、昆明5个城市在同一类。
类间平方和在总平方和中的占比越大越好,在做K均值聚类分析时该指标可用于确定较优的聚类数K,可由小到大改变K的值,找出使该占比达到最大的K,K也不能太大,否则分类太琐碎。在K取4时,类间平方和在总平方和中的占比为77.8%;在K取5时,类间平方和在总平方和中的占比为81.9%。因此选择将全国31个主要城市按空气质量进行分类最好分为5类。
3 城市空气质量主成分分析
3.1 多元回归和逐步回归
依据处理之后的全国31个主要城市空气质量的数据表先做线性回归分析。回归结果见表4。表中x1、x2、x3、x4、x5、x6分别对应PM2.5、PM10、SO2、CO、NO2、O3浓度。

表4 线性回归分析结果
从上述输出结果可以看出,回归方程是非常显著的,R2为0.947,模型拟合效果很好,但x2、x3和x4的回归系数没有通过显著性检验(在0.05的显著性水平下)。回归方程为
y=142.756-1.020x1-0.243x2+0.159x3-
9.112x4+0.736x5-0.321x6
(1)
也可进行逐步回归,逐步回归结果见表5。

表5 逐步回归结果
从输出结果可见,回归方程显著,系数x3不显著,R2为0.945,模型拟合效果很好,逐步回归所得方程为
y=135.331-0.947x1-0.328x2+0.161x3+
0.658x5-0.263x6
(2)
3.2 主成分分析和主成分回归
做主成分回归分析,先求样本相关系数矩阵,结果见表6。
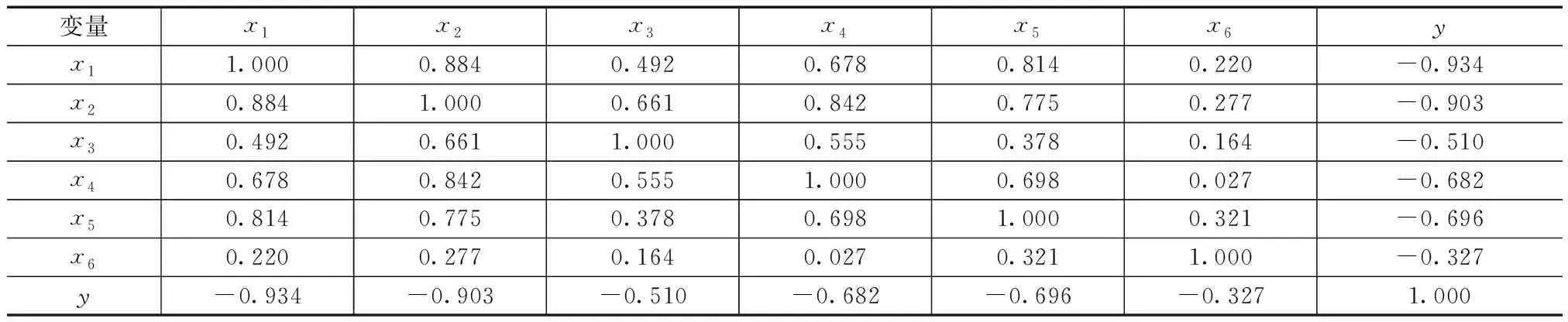
表6 样本相关系数矩阵
可见,x1、x2与y两两高度相关,可用主成分降维,主成分回归结果见表7。

表7 主成分回归结果
前3个主成分累积贡献率已超过91%,故选择前3个主成分就够了[12]。也可采用矩阵形式来做主成分回归。前3个主成分分别为

(3)

(4)

(5)
下面计算样本主成分,并将第1、第2和第3主成分得分放入数据库的后3列,记作z1、z2和z3,再作响应变量y关于3个主成分z1、z2和z3的回归分析,结果见表8。

表8 主成分回归分析结果
可见,作y关于3个主成分z1、z2和z3的回归分析效果理想,回归方程和其中两个回归系数是显著的,R2为0.809,主成分回归方程为
y=68.194-7.775z1-2.332z2-5.675z3
(6)
可以利用主成分与原来自变量间的关系z*=PTx*将主成分还原为原来的自变量,将主成分z1、z2和z3还原为原始变量后所得回归方程为
y=132.999 7-0.292 9x1-0.149 7x2+
0.075 9x3-16.484 5x5-0.511 2x6
(7)
这个回归方程是从主成分回归方程变形而来的,最初回归方程中x2、x3和x4的回归系数不显著,主成分所得回归方程更为合理。从方程可以看出,x5所对应的指标NO2对空气质量的影响最大。
4 降低空气污染的对策建议
4.1 从污染源上进行控制
工业发展的同时造成了空气污染,工业污染物的排放是空气污染的重要原因之一。从污染源上进行控制需要监管工业污染源的排放,控制城市道路施工和扬尘。对于工业高耗能、高污染项目进行评估,严格控制高耗能、高污染项目的实施。对城市道路施工进行管理,降低施工扬尘污染;对道路运输车辆进行管理,严格查处车辆扬尘的现象,加强道路保洁和洒水降尘工作力度。
4.2 控制空气污染物的排放
提倡绿色出行,控制私家车的数量,鼓励公民出门减少私家车的使用,尽量乘坐公共交通或骑自行车。以此降低汽车尾气排放,从而减少相应的氮氧化物、颗粒物和一氧化碳这些空气污染物的排放。加大公共交通的发展,增加地铁、公交线路以提高运载量,对机动车燃气改造,比如出租车和公交车实行油改气、油改电等措施,从根源上减少空气污染物排放。
4.3 加强环保宣传教育
提高民众环保意识,实现对广大民众的环保教育,需要国家与政府鼓励环境教育与环保建设,对环保工作给予政策上的支持;通过媒体进行形式多样的环保建设宣传,培养公众的环境意识,提高全民参与环保的意识,使人们充分认识到生态环境污染对经济发展、社会稳定和人类生存的危害性。倡导公民从生活中一点一滴的小事做起,切实践行环保。
