高烈度区独塔自锚式悬索桥纵向减震体系研究
2022-05-20庄鑫
庄鑫
(上海市城市建设设计研究总院(集团)有限公司,上海200125)
1 引言
自锚式悬索桥不需要设置庞大的重力式地锚,对不同地质条件有很好的适应性[1],在100~600 m 跨径范围均有较强的经济性优势。独塔自锚式悬索桥以其优美的造型、灵活的布置性和良好的适用性备受桥梁建设者的青睐。特别是对于城市景观要求较高,主跨跨径在100~300 m 的桥梁中,独塔自锚式悬索桥正在越来越多地被应用。
与地锚式悬索桥不同,自锚式悬索桥在缆—塔—梁三者的传力路径与约束关系上更贴近斜拉桥[2],在地震作用下,梁体的惯性力主要通过主缆以及塔—梁、墩—梁间连接传递给桥塔和桥墩再传至基础。因此,自锚式悬索桥的地震反应及抗震性能与其结构体系密切相关。
目前,国内外学者对独塔自锚式悬索桥的纵向减震体系进行了一定的研究。管仲国等[3]以南京江心洲大桥为例,研究了独塔自锚式悬索桥采用弹塑性阻尼器作为减震装置的适用性,研究表明弹塑性阻尼器可以非常有效地用于自锚式悬索桥减隔震设计;王宇等[4]以平胜大桥为例,研究了独塔自锚式悬索桥的减震体系,研究表明,大跨度自锚式悬索桥适合采用飘浮体系,在悬索桥塔梁结合部设置了摩擦摆式支座能够满足结构的隔震需要;张超等[5]以鼓山大桥为例,研究了独塔自锚式悬索桥纵向设置黏滞阻尼器的减震效果,研究表明,在主桥纵桥向安装黏滞阻尼器可以有效地改善结构的变形及位移,改善结构特别是关键结构部分的受力,使结构更为合理。
尽管目前针对自锚式悬索桥纵向减震体系国内外学者已经做了一些研究,但是由于高烈度区自锚式悬索桥建设经验较少,针对高烈度区自锚式悬索桥抗震性能研究及减隔震设计尚显不足。为此,本文以某拟建兰州黄河大桥为背景,研究高烈度区独塔自锚式悬索桥纵桥向减震体系,并对减震装置参数进行优化设计。
2 工程案例
2.1 工程概况
本文以某拟建兰州黄河大桥为工程背景。该桥主桥为独塔自锚式悬索桥,主塔为四立柱桥塔,主桥跨径布置为41 m+110 m+200 m+26 m(见图1),桥面全宽44 m。主梁主跨200 m与配跨26 m 为钢箱梁结构,单箱三室截面,标准梁高为3.2 m。主梁边跨110 m 与配跨41 m 为双叠合梁结构,箱室布置与梁高与钢箱梁段一致。主桥基础采用群桩基础,为钻孔灌注桩,主塔桩基桩径为2.0 m,过渡墩和辅助墩桩基桩径为1.5 m。
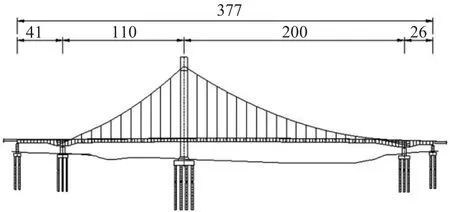
图1 主桥立面图(单位:m)
2.2 地震动输入
本文根据JTG/T 2231-01—2020《公路桥梁抗震设计规范》进行抗震分析,主桥取阻尼比0.02 时E2 地震作用下加速度反应谱作为水平向和竖向地震输入,根据水平向和竖向反应谱分别拟合3 条人工时程曲线,计算结果取3 条时程曲线计算结果的包络值。
拟建桥梁所处的兰州地区抗震设防烈度为Ⅷ度,属高烈度区,设计基本地震加速度为0.20g。场地类别为Ⅱ类场地,场地特征周期为0.45 s。图2 为其中一条水平向人工拟合时程曲线图示,图3 为水平向人工时程曲线拟合反应谱与规范反应谱对比。

图2 水平加速度时程相位曲线(阻尼比0.02)
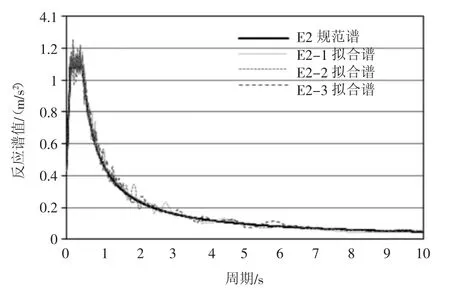
图3 水平向人工时程曲线拟合反应谱与规范反应谱比较
3 纵向减震体系选择及模型建立
3.1 纵向减震体系选择
根据以往的研究及工程经验可知,高烈度区大跨度独塔自锚式悬索桥适合采用飘浮体系或半飘浮体系,因为塔梁固结体系会导致桥塔在地震作用下承担几乎全桥的地震力,对桥塔的抗震安全极其不利,需要增加桥塔及基础的尺寸,经济性上也是不可取的。飘浮体系或半飘浮体系下,塔梁之间可以设置合理的纵向减震装置,以达到良好的抗震效果,既能保证桥梁结构安全,又不会显著增加造价。
独塔自锚式悬索桥纵桥向减震体系常用的减震装置有黏滞阻尼器、金属阻尼器、摩擦摆式支座等。金属阻尼器的屈服力和变形能力是一对矛盾,难以同时满足大屈服力和大变形能力的需求。由于自锚式悬索桥具有低阻尼的结构特性,黏滞阻尼器拥有更好的耗能能力,应用在自锚式悬索桥上会得到更好的减震效果。此外,自锚式悬索桥的温度变形较大,黏滞阻尼器的使用不会对悬索桥的温度变形等正常使用性能产生不利影响[6]。因此,本文推荐在塔梁之间设置黏滞阻尼器作为纵向减震体系,墩梁之间纵向设置普通球钢支座。
3.2 桥梁动力计算模型建立
本文采用有限元程序Midas Civil 建立了独塔自锚式悬索桥三维有限元线性分析模型,对成桥状态进行地震响应分析。模型利用空间框架单元模拟主塔、主梁、墩柱,利用只受拉桁架单元模拟主缆及吊索,考虑主塔、主缆及主梁恒载作用对结构刚度的影响;各主塔、桥墩基础采用六弹簧模拟,基础刚度由“m 法”确定。
塔梁之间纵向设置黏滞阻尼器,黏滞阻尼器采用Maxwell计算模型进行模拟。
滑动型球钢支座采用滞后系统单元模拟,其恢复力模型如图4所示。图中,Fmax为滑动摩擦力,x为上部结构与墩顶的相对位移,xy为屈服位移。弹性恢复力最大值与滑动摩擦力相等,即:
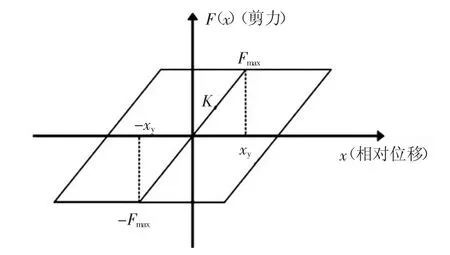
图4 滑动支座恢复力模型

式中,K为支座初始刚度;f为滑动摩擦系数,边墩与主塔处球形钢支座的滑动摩擦因数取2%;N为支座恒载反力;屈服位移xy取2 mm。
4 减震效果分析及减隔震参数优化
对于纵向飘浮或半飘浮体系,主梁纵向地震位移难以得到有效控制;对于塔梁纵向固定体系,尽管主梁位移可以得到很好的控制,但是桥塔地震力会十分巨大。本文针对前述减震体系进行结构地震响应分析,与纵飘体系及塔梁固定体系进行比较,研究其减震效果,并对减隔震参数进行优化分析。
4.1 减震体系减震效果分析
图5~图7 给出了纵飘、塔梁纵向固定约束、塔梁间设置纵向黏滞阻尼器(阻尼系数C=2×3 000,速度指数ξ=0.3)3 种约束体系下的梁端地震位移、塔底地震剪力等响应结果。

图5 不同约束体系下梁端地震位移响应曲线
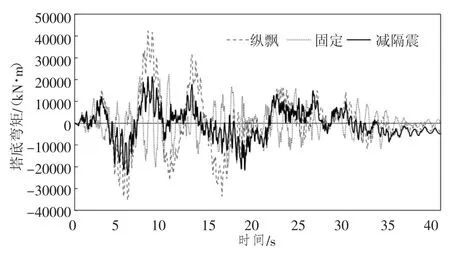
图7 不同约束体系下塔底地震弯矩响应曲线
通过比较上述结果可知,塔梁纵向飘浮体系下梁端位移和塔底弯矩最大,塔梁纵向固定约束体系下塔底剪力最大而梁端位移最小。与之相比,塔梁间设置纵向黏滞阻尼器的减隔震体系下,各地震响应均得到有效控制,与纵飘体系相比,梁端位移和塔底弯矩减震率达到50%以上;与塔梁纵向固定体系相比,塔底剪力减震率达65%。
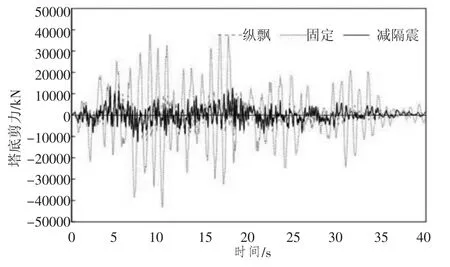
图6 不同约束体系下塔底地震剪力响应曲线
综上所述,塔梁之间设置纵向黏滞阻尼器对高烈度区自锚式悬索桥来说是有效的减震体系。
4.2 减隔震参数优化分析
对于黏滞阻尼器而言,选取不同的参数,桥梁结构地震响应也不尽相同。为选取合理的阻尼器参数,现对黏滞阻尼器进行参数敏感性分析。
本文中主塔处设置2 个阻尼器,左右各1 个,单个阻尼器的速度指数ξ 取值范围0.2~0.5,阻尼系数C取值范围1 000~5 000,位移的单位为m,阻尼力的单位为kN。通过前述纵向+竖向地震输入下的非线性时程分析,对设置不同参数黏滞阻尼器后结构关键部位的地震响应进行分析比较,以选择适宜的阻尼器参数。
从图8~图11 可知,当速度指数从0.2 增大到0.5 时,塔顶位移、梁端位移及塔底弯矩响应总体呈增大趋势,塔底剪力呈减小趋势,阻尼速度指数推荐采用ξ=0.2,但整体来看速度指数影响较小。
从图8~图11 可知,当单个阻尼系数C从1 000 变化到5 000 时,塔顶位移、梁端位移及塔底弯矩响应总体呈减小趋势,且减小幅度逐渐变缓;塔底剪力呈增大趋势。综合考虑地震位移、地震内力控制效果及黏滞阻尼器安装费用,阻尼系数推荐采用C=2×3 000(横向设置2 个阻尼器,单个阻尼器阻尼系数取3 000)。

图8 塔顶位移响应随阻尼参数变化图

图9 梁端位移响应随阻尼参数变化图
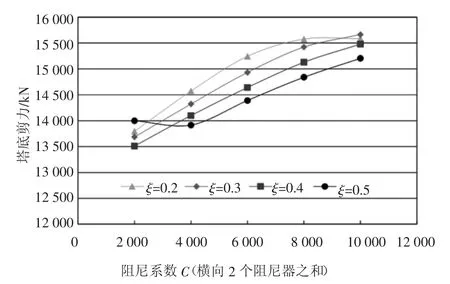
图10 塔底剪力响应随阻尼参数变化图
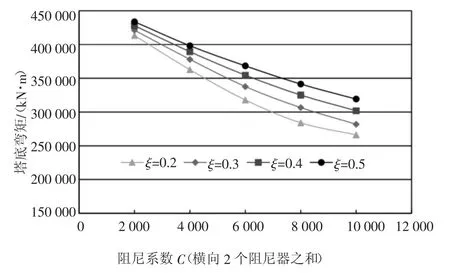
图11 塔底弯矩响应随阻尼参数变化图
5 结论
本文以兰州市某拟建独塔自锚式悬索桥为背景,分析了纵桥向不同约束体系下结构地震响应,并对减隔震装置参数进行优化分析,得到如下结论:
1)与纵向飘浮/半漂浮体系相比,塔梁之间设置黏滞阻尼器可以有效控制结构地震位移响应,与纵向塔梁固定体系相比,塔梁之间设置黏滞阻尼器可以有效减小结构的地震内力响应,塔梁之间设置纵向黏滞阻尼器对高烈度区自锚式悬索桥来说是有效的减震体系。
2)通过黏滞阻尼器参数优化分析发现,阻尼系数越大,减震效果越好,但是当阻尼系数增加到一定程度后,减震效果逐渐减弱。另外,随着阻尼系数增加,其经济效益逐渐变差,阻尼器布置和局部连接的设计也会变得困难。
3)分析发现,与阻尼系数相比,阻尼器的速度指数总体来说对桥梁结构地震响应影响较小。
4)桥梁抗震设计需综合考虑结构地震位移响应、地震内力响应以及经济效益等因素,阻尼器参数的确定应针对上述目标进行综合分析,合理选择。
