相控阵天线非对称方向图波束赋形研究

张华美，徐 诚，王芳芳，3

(1.南京邮电大学电子与光学工程学院，江苏南京 210023 2.东南大学毫米波国家重点实验室，江苏南京 210096 3.南京邮电大学射频集成与微组装技术国家地方联合工程实验室，江苏南京 210023)

随着科技的不断发展，在无线通信系统中人们对天线辐射方向图的要求越来越高，而利用波束赋形技术可以改变天线辐射方向。相控阵的波束赋形通过改变各天线单元的幅度与相位来改变阵列天线的方向图。在实际应用中，由于天线各个激励单元幅度相位分布不规则，且无很好的数学方法对天线馈电进行设计，所以需要应用一些优化算法来寻找满足设计要求的幅度相位分布。

结果表明，利用粒子群优化算法可以提高天线阵列指向性并得到更低的旁瓣电平［1-3］。通过阵列分割聚类或者智能优化的方法优化阵列天线的馈电，进而影响天线阵列产生的方向图，这种方法也得到包括非对称方向图的任意波束方向图［4-5］。在二维的天线平面阵中也可以利用优化算法优化波束指向［6-7］。针对粒子群算法过早收敛于局部最优解的问题，目前的研究通常采用改进算法机制或将两种算法相融合的方法予以解决。比如在优化算法的粒子生成阶段，利用混沌算子的无序和遍历性改变初始粒子集或迭代步长，提高算法的全局搜索能力［5，8-10］。 或者考虑粒子群算法本身，在算法中引入自适应权重，结合差分进化策略，丰富算法种群个体信息，增强优化算法的全局收敛性［11］；利用网格划分粒子群的方法，细化初始粒子群，将局部最优解步步分割最终得到更优的全局最优解，提高收敛速度［12］；在粒子群原有的寻优基础上引入双重更新策略，提高全局搜索能力［13］。也有学者将粒子群算法与模拟退火算法、蚁群算法等其他优化算法的优点相融合，使得融合后的新算法相较于基础算法拥有更高的运算效率［14-15］。

本文提出一种针对非对称方向图的相控阵天线设计方法，即一种新的改进粒子群优化算法。在该算法中，为解决粒子群算法容易收敛于局部最优解的问题，引入了莱维因子与蝴蝶算法的局部搜索机制。莱维因子在每代粒子更迭之后产生随机的小范围扰动，可以提高粒子群算法摆脱局部最优解的能力。蝴蝶算法与粒子群算法流程类似，都是通过粒子迭代更新达到最优解，不同点在于蝴蝶算法还引入了香味强度函数，以及寻找全局最优解对应的公式。将蝴蝶算法的粒子全局搜索原理引入到粒子群算法中，能得到更好的全局最优解。将改进的粒子群优化算法用于实现阵列天线在左右不同分贝的低副瓣电平。实验结果表明相较于基础优化算法，本文算法具有收敛速度快，寻优能力强的特点。

1 一维直线阵列天线模型

相较于一个单元天线，阵列天线可以实现多样化的辐射特性，尤其可以形成特定形状波束，以实现某特定区域的电磁波覆盖。这种改变空间内电磁波分布的特殊性使得阵列天线可以被用来实现波束赋形。将各单元沿直线排列看作线性阵列，如图1所示。

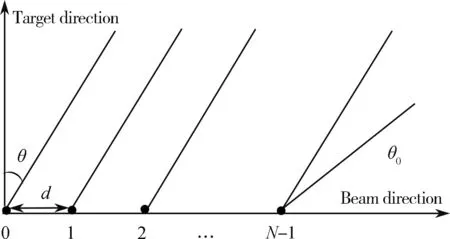
图1 直线阵列排布示意图

根据阵列天线中的理论，假设每个天线单元均为理想全向天线，天线阵方向图的公式为

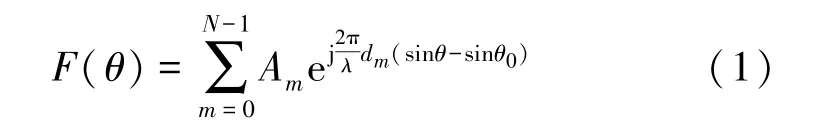
式中，Am为各天线单元的激励，N指天线单元的个数，θ与θ0分别为波束入射角与波束扫描角度，dm为天线间距。将Am写作幅度与相位的形式，指数相乘的位置合并。相位延迟扫描的公式定义为

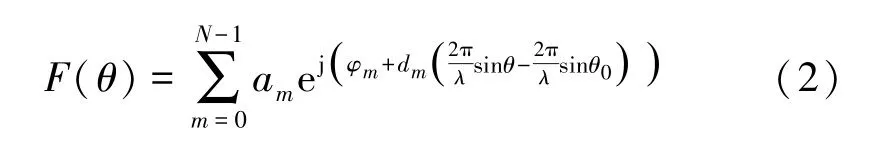
式中，am为激励幅度，φm为激励相位。从式（2）可以看出，改变天线阵方向图的因素包括天线单元的激励、天线单元的个数、天线间距。对于非对称的方向图，需要对天线馈电的相位，或者同时对幅度与相位进行迭代寻优。

阵列天线可以通过改变馈电的幅度与相位，改变整个天线阵的方向图，从而实现波束赋形。而在民用移动通信领域、军用雷达领域、军民共用的遥控遥测领域等，不仅要求天线生成的方向图具有较低的副瓣包络，往往还要求在一定的角度范围内形成特殊波束［16］。左右不同分贝的副瓣波束指在主瓣两侧的副瓣小于等于不同的预设值。这两种方向图的设计被应用于军事侦察或电子对抗之中。本文针对等间距阵列天线，将天线馈电的幅度与相位作为优化要素进行阵列天线非对称方向图的波束赋形。

2 改进粒子群优化算法在天线阵列优化中的应用

粒子群优化算法是一种通过模拟自然界中鸟群觅食的过程实现的智能优化算法。在可行解空间中初始化一组粒子，每个粒子都代表优化问题的潜在最优解。通过设计评分规则评价每个粒子对应解的优劣程度，反复迭代最终得到最符合优化目标的最优解［9］。粒子更新速度的公式为

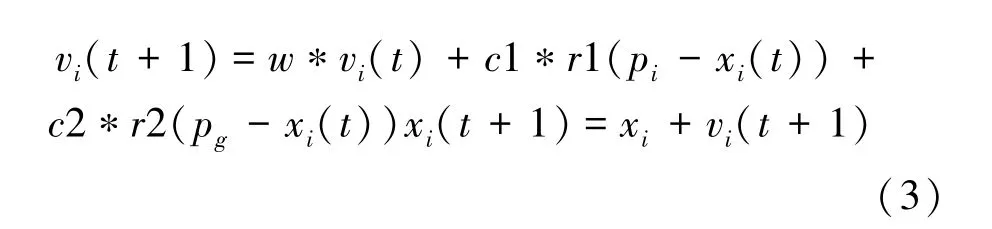
式中，xi为待优化的参数，包含天线馈电的幅度与相位，通过反复迭代使得最后结果更接近预期结果；w指上一代速度所占比例；vi为每一代粒子移动的速度；pi为第i个粒子经历的最优位置；pg为所有粒子的全局最优解；c1、c2为学习因子，一般被设计为2。在这里对适应函数进行重新设计，为了实现左右副瓣优化的目标，适应度函数为

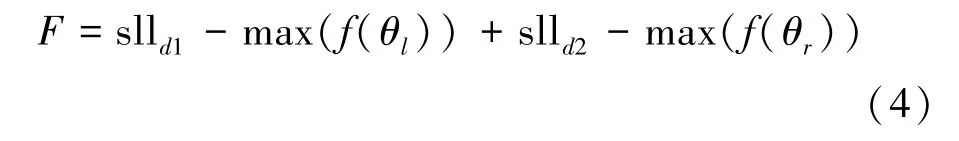
式中， max（f（θl）） 和 max（f（θr）） 分别表示主瓣左右两侧的最大副瓣，slld1与slld2分别表示预期的左右副瓣值，适应度值F表示优化模式与预期模式之间的差异。

由于粒子群优化算法在求解过程中存在“早熟”现象，即迭代前期会快速收敛至局部最优解，迭代后期寻优能力减弱，为解决这一问题，引入另一种智能优化方法蝴蝶算法［17］的局部搜索思路，提高粒子群算法的后期搜索能力。蝴蝶利用自身的感知器定位食物的来源。该算法中，假设每只蝴蝶产生一定强度的香味，这些香味会传播并被区域内的其他蝴蝶感知。每只蝴蝶释放出的香味与它的适应度有关。蝴蝶算法本身具有全局搜索与局部寻优两种迭代公式，选择局部寻优公式并加入莱维飞行因子［18］更新粒子，提高后期收敛能力。具体更新计算公式为

式中，f（x）为香味强度函数，c表示感官形态系数；I为适应度函数值，a为［0，1］之间的随机数。感官形态系数c计算公式为

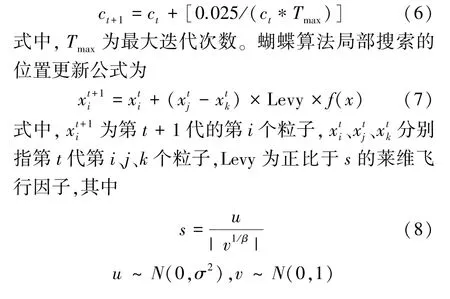
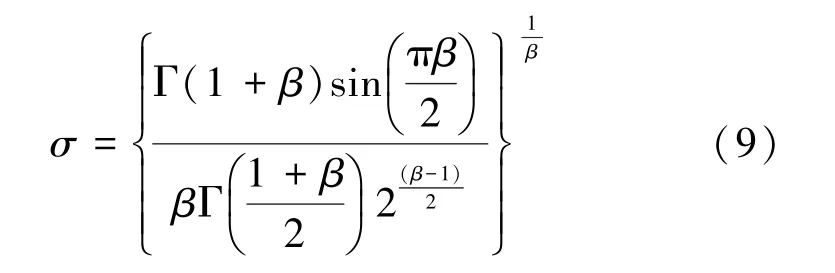
式中，Γ表示伽马分布函数，u，v为服从正态分布的随机数，β为常数，取1.5。

为将两种智能算法相融合，采用以下优化策略，先通过粒子群算法产生粒子并计算适应度值，然后利用蝴蝶算法的局部更新策略更新粒子，计算新粒子适应度值。将两种算法产生的粒子混合后按适应度值大小重新排序，最后利用“精英”筛选思想，即选出评分靠前的粒子，进入下一次迭代过程，并更新群体最优解。具体流程图如图2所示。

3 结果与分析

为验证算法的有效性，针对以下案例进行优化。考虑一个24单元的理想全向直线阵列，间距为0.5倍波长。分别采用粒子群算法（PSO）、蝴蝶算法（BOA）、改进的粒子群算法BPSO进行优化计算，种群数M＝200，每个被优化粒子为2*24的矩阵，对应每个天线单元馈电的相位与幅度，相位取值空间［a，b］ ＝ ［0°，60°］，幅度取值以泰勒分布在-35 dB的幅度为基础，在［-0.1，0.1］的范围内浮动，最大迭代次数为500，惯性常数为0.9，加速度常数为c1＝c2＝2。目标方向图主瓣左侧副瓣大小为-40 dB，右侧副瓣大小为-30 dB。其中生成的迭代曲线如图3所示，最优解对应的馈电幅度与相位如表1所示，BPSO生成的最优解方向图结果如图4所示，3种优化算法计算结果如表2所示。

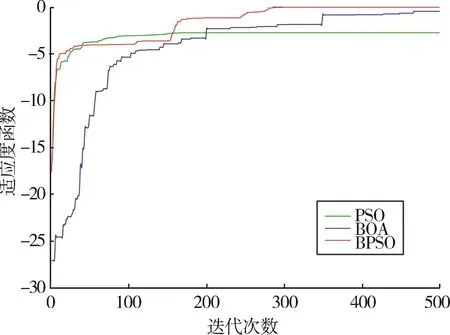
图3 不同优化算法的迭代曲线

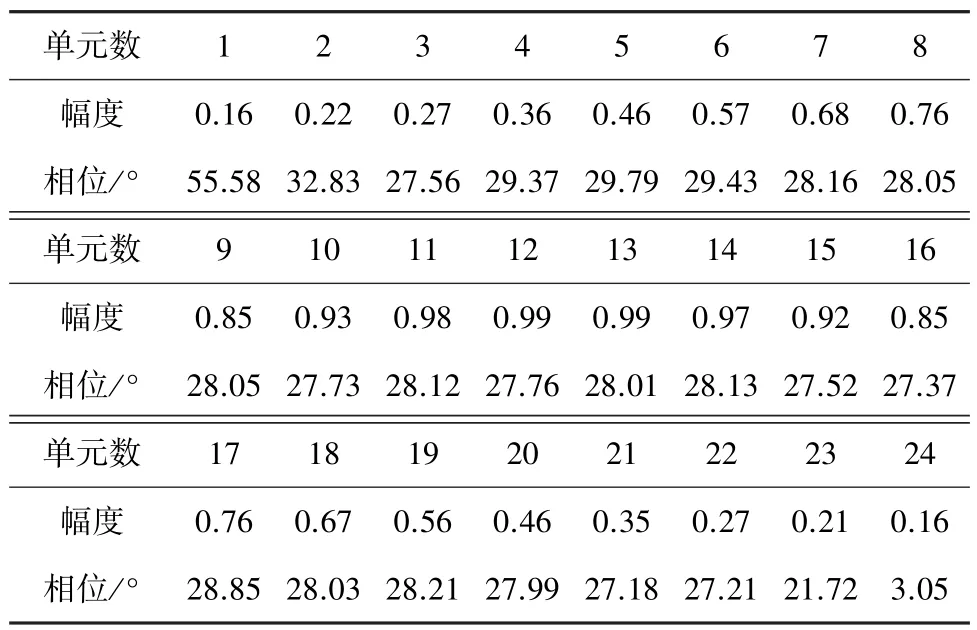
表1 最优结果对应的馈电幅度与相位

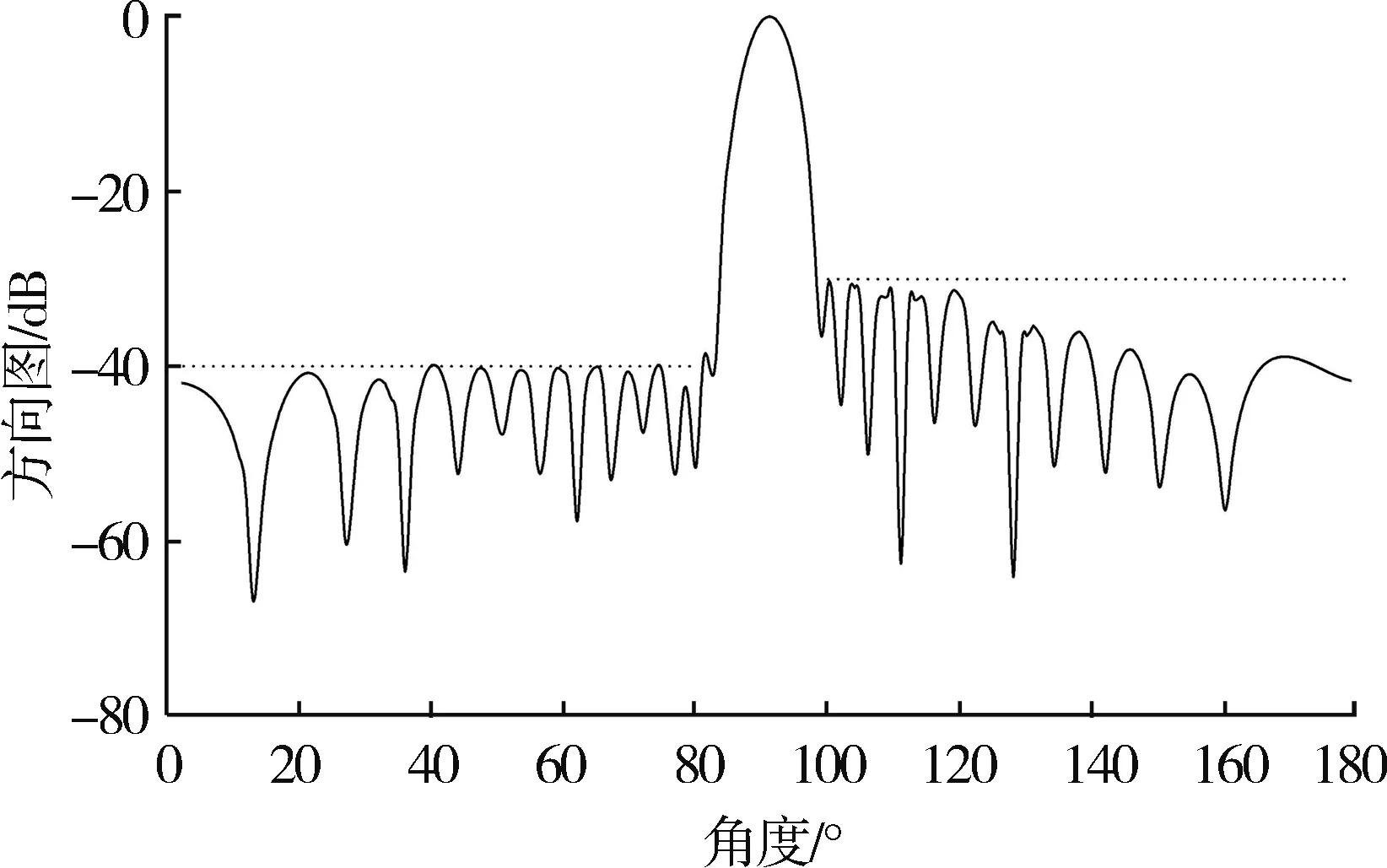
图4 BPSO生成最优解方向图

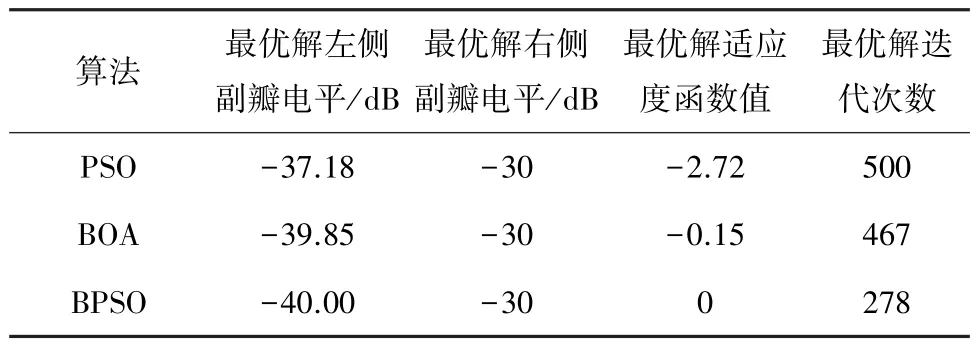
表2 三种优化算法实验结果

根据实验结果可以得出，由于粒子搜索维度较高，PSO算法不能通过迭代得到适应度值为0的全局最优解，只能在迭代至278代时收敛到适应度值为-2.72的局部最优解。而BOA算法和BPSO算法可以得到全局最优解，同时根据图3可以看出BPSO算法在迭代100次之前收敛速度明显优于BOA算法。综上，BPSO算法与基础优化算法相比在收敛速度和寻找全局最优解两个方面具有很大的优势。

4 结束语

针对非对称方向图相控阵天线优化问题，本文在粒子群算法的基础上引入了蝴蝶算法中的局部搜索能力与莱维随机游走策略，采用“精英”粒子筛选模式，将二者结合并提出了一种新的改进粒子群优化算法，同时对阵列天线馈电的幅度与相位进行优化，实现了天线阵非对称低副瓣方向图的目标。该算法相较于基础优化算法具有收敛速度快，寻优能力强的特点，为相控阵波束赋形的计算与研究提供了一种有效的解决方案。