HNS 溶解度与介稳区的光流控测定方法研究

2022-05-19周星屹闫樊钰慧曹金乐石锦宇吴立志沈瑞琪

含能材料 2022年5期

周星屹，闫樊钰慧，曹金乐，石锦宇，朱朋，吴立志，沈瑞琪

（1. 南京理工大学化学与化工学院，江苏南京 210094；2. 微纳含能器件工业和信息化部重点实验室，江苏南京 210094）

1 引言

炸药的晶体结构形态是影响其能量释放、安定性、相容性、力学与环境适应性的重要因素［1-3］。获得综合性能优异炸药晶体的关键步骤之一，是对其结晶过程进行监测，使结晶过程清晰可控，为结晶过程的控制提供理论支撑［4］。结晶过程从热力学角度出发可以看做是从一个固液平衡态到另一个固液平衡态的过程，这个过程中存在着能量的产生和消耗，这种能量的转化作为结晶的推动力［5］。因此，研究炸药结晶热力学是控制与理解炸药结晶过程的重要一步。

目前，国内外对结晶热力学的研究主要集中在对晶体溶解度、介稳区宽度等热力学参数的测定［6-13］，分为间接测定法与直接测定法［5］。间接法即采用折射率、电导率、浊度等物理量来判定过饱和溶液中出现首批晶核导致物性改变的方法，但其存在测量精度不高、晶核出现时刻难以判定等缺点；直接法即采用目测、激光等手段来直接判定过饱和溶液产生首批晶核的方法，虽然分别具有方法简单、精度较高等优势，但其仍是在宏观尺度下的测量。而对于临界晶核此类尺寸处于纳米级的物质而言，一种尺度更接近于其自身尺寸的测定方法则更为适用。

近年来，随着人们对芯片实验室（LOC）、微全分析系统（μTAS）、微机电系统（MEMS）等技术的关注和投入，研究者们发现，当微流控和光学两个独立的部分结合在一起时，两部分之间可产生协同作用，其功能远远大于单独一种技术或者简单两种技术的加和，可实现更多的功能和应用［14］，继而提出了光流控这一概念。光流控的应用可分为两方面，一方面是利用光来控制流体的特性和运动，主要是利用光学或者基于微机电系统光学器件来控制流体的特性，例如：光镊［15］、光控微阀［16-17］等；另一方面则是利用微流控来控制光，例如：微流体透镜［18-20］、流体光纤［21］等。光流控方法的出现为炸药结晶热力学参数的测定提供了新的思路。

为了进一步提升临界晶核测定精度、缩短测量时间，本研究提出了一种基于光流控的炸药结晶热力学参数的测定方法，将激光发生接收装置与微流控芯片相结合，构建了适用于结晶热力学参数测定的实验装置，并以HNS 炸药为样本对此测定方法的适用性进行了验证。利用该方法测定了HNS 在不同配比DMSO/DMF 溶剂体系、不同起始温度下的溶解度与介稳区宽度，通过对温度、时间与激光信号间关系的分析与处理，得到了一系列结晶热力学参数。

2 实验部分

2.1 试剂与原料

二甲亚砜（DMSO），分析纯，国药化学试剂有限公司；二甲基甲酰胺（DMF），分析纯，国药化学试剂有限公司；乙醇，纯度99.7%，国药化学试剂有限公司；去离子水，自制；六硝基茋（HNS），纯度≥97.2%，湖北东方化工有限公司。

2.2 实验装置

本研究将激光发生接收装置与微流控芯片相结合，采用动态激光法对HNS 的溶解度与介稳区宽度进行检测，测试系统如图1 所示。

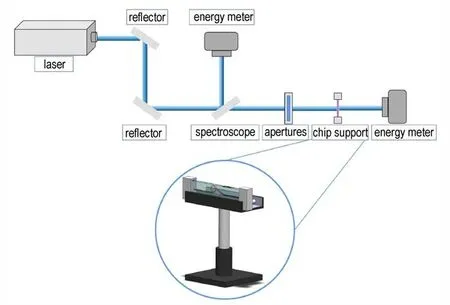
图1 基于光流控方法的测试系统Fig.1 Testing system based on optofluidics method

测试系统由激光发生装置、反射镜、分光镜、光阑、芯片支架、微流控芯片和在线能量计等部件组成。其中，激光器型号为Nd：YAG 脉冲激光器（波长为1064 nm，脉宽为65 ns），最大脉冲能量800 mJ。在光路系统构建完毕后，需要对激光能量进行标定，采用激光能量计（Model 30A，Ophir，以色列）测量不同电压下的激光能量，在每个电压示数下，测量10 次求平均值，以得到激光器控制面板电压数值与实际激光能量的对应关系。

微流控芯片为一带有圆形结晶腔室的单通路PMMA 芯片，其微通道的宽度与深度均为0.5 mm，圆形腔室的直径与深度分别为10 mm 与0.5 mm，其示意图与实物图如图2 所示。其腔室中埋有微型温度传感器，用于芯片中溶液温度的实时测量。利用芯片支架将微流控芯片置于偏振片与能量接收器的中间，调整芯片支架高度使激光束打在结晶腔室的中心位置。

2.3 溶解度的测定

动态激光法测定溶解度的原理为：光在通过非均相体系时会发生弹性散射现象，在晶核形成的时刻，光被晶核散射而导致接收到的透射光强度减弱，溶液中晶核浓度与接收到的光强度具有正相关性，通过测量溶液的透射光强度随时间的变化可检测溶液中晶体的溶解和成核过程，进而获得其溶解度。

研究采用动态激光与微流控芯片相结合的方式测定HNS 在不同配比DMSO/DMF 混合溶剂体系中的溶解度。与静态溶解度测定方式相比，动态激光法测量时间短、测定效率高、样品消耗量少，能够有效减少实验误差。混合溶剂中溶解度（摩尔分数）的计算公式为：

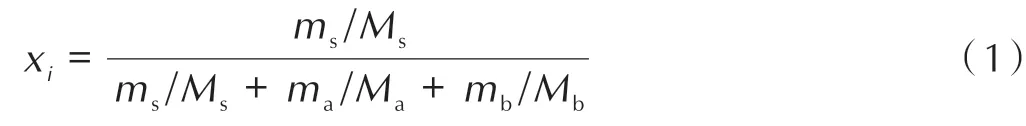
式中，xi为HNS 的溶解度；ms为溶质HNS 的质量，g；Ms为溶质HNS 的摩尔质量，g·mol-1；ma为溶剂DMSO 的质量，g；Ma为溶剂DMSO 的摩尔质量，g·mol-1；mb为溶剂DMF 的质量，g；Mb为溶剂DMF 的摩尔质量，g·mol-1。

测定的主要实验过程如下：

（1）将DMSO 与DMF 分别按体积比10∶0，7∶3，5∶5，3∶7，0∶10 配制5 种DMSO/DMF 溶剂体系，量取5 种配比的溶剂于干燥洁净的烧杯，并向各烧杯中加入2 mg HNS 原料，之后将烧杯置于恒温水浴锅，起始温度设置为318.15 K。

（2）打开激光器，设置控制面板电压为630 V，脉宽为65 ns，调整微流控芯片支架位置，检查光斑是否落在结晶腔室的正中央，打开能量计和数据软件，对数据进行记录。

（3）将配制好的溶液使用注射器通过微通道注入结晶腔室内，采集激光在结晶腔室前后的能量值并通过软件进行实时记录。此时溶液处于不饱和状态，激光信号值最大，入射光与出射光能量平行。

（4）每次向体系中加入0.2～0.5 mg 的HNS 原料。重复上述操作，直到激光信号值出现衰减且5 min 内不再升高即达到溶解终点，记录此时HNS 的加入量与注射量。

（5）测定318.15，323.15，328.15，333.15，338.15，343.15，348.15 K 和353.15 K 下HNS 在体积比为10∶0，7∶3，5∶5，3∶7，0∶10 的DMSO/DMF 溶剂体系中的溶解度。所有温度点均按照上述操作进行溶解度的测定。为保证数据准确性，每个温度点重复测量3 次，取算术平均值作为各温度下的溶解度。

2.4 介稳区宽度的测定

结晶介稳区是超溶解度与溶解度曲线之间的区域。因此，起始温度T0与降温结晶临界温度Tnuc的差值即为介稳区宽度。HNS 在5 种配比溶剂中介稳区宽度测定的主要实验过程如下：

（1）根据溶解度测定实验中得到的溶解度数据，精确配制318.15，323.15，328.15 K 和333.15 K 的4 组温度下不同溶剂体系的饱和HNS 溶液。

（2）调节恒温水浴锅温度高于起始温度3 K，充分搅拌至HNS 全部溶解。

（3）将溶液使用注射泵注入结晶腔室，并同步开启激光系统与温度传感器记录仪，溶液降温至结晶临界温度Tnuc时，激光信号出现衰减，这说明检测到晶核的形成，记录此时的温度点。为保证实验数据准确，重复3 次上述操作，并取算术平均值作为最终介稳区宽度。

3 结果与讨论

3.1 溶解度的测定

3.1.1 溶解度模型

结晶过程是固体物质以晶体状态从气态、液态与熔融中析出的过程，该过程的推动力源自结晶物系热力学的非平衡性［22］。HNS 的降温结晶属于典型的溶液结晶过程，属于固液相平衡（solid liquid equilibrium，SLE）范畴。基于SLE 的溶解度模型［23］建立方法主要包括状态方程法、经验模型法、人工神经网络法等。其中，经验模型的理论基础虽较其余两种方式的更薄弱，但具有针对性强，所需物性参数少且精度高的优势。所以本研究采用Apelblat 模型［24］、λh模型［25］对收集到的溶解度数据进行拟合。

此外，为保证模型的适用性与准确性，采用均方根偏差［26］（RMSD）对溶解度测定值与模型拟合值之间的差异进行评估：

式中，x为溶质溶解度；T为实验温度，K；A、B、C为Apelblat 模型中的模型参数。通过软件对x和T进行该模型下的拟合回归，即可得到模型参数A、B、C。

（2）λh 模型

Buchowski 等提出的λh模型适用于多元混合溶剂体系，模型相关性高且测试结果准确。其表达式如下：

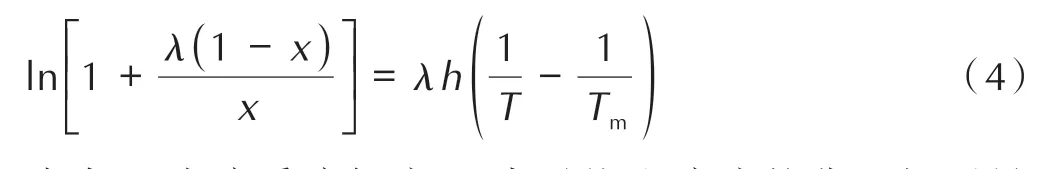
式中，x为溶质溶解度；λ表示饱和溶液的非理想型量度；h表示焓因子；Tm为溶质的熔点，K；T为实验温度，K。λ和h是λh模型的模型参数，通过x与T的函数关系，即可通过数据回归求出模型参数λ和h。

3.1.2 HNS 在不同溶剂体系下的溶解度测定

实验测定了自318.15 K 起至353.15 K，HNS 在体积比为10∶0，7∶3，5∶5，3∶7，0∶10 的DMSO/DMF 溶剂体系下的溶解度数据。根据测定数据以及式（1），得到HNS 在各实验参数下的溶解度。HNS 溶解度与溶剂体系和温度的关系如图3 所示。由图3 可知，随着温度的升高，HNS 在这5 种体系中的溶解度均增大，且溶解度曲线较陡，说明HNS 溶解度随温度变化敏感，即意味着以上5 种溶剂体系都可以作为HNS 降温结晶的溶剂；同时，随着体系中DMF 体积的增加，HNS溶解度减小，这是因为DMF 的极性弱于DMSO 的，HNS 更容易与极性大的溶剂作用而产生溶解。

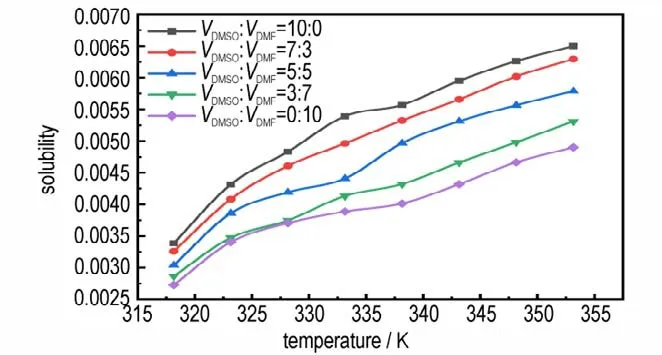
图3 HNS 在5 种DMSO/DMF 溶剂体系下温度与溶解度的关系Fig.3 Relation between temperature and solubility of HNS in 5 DMSO/DMF solvent systems

采用Apelblat 模型对实验数据进行拟合关联，图4 为VDMSO∶VDMF=10∶0 溶剂体系下温度与溶解度的拟合关系。

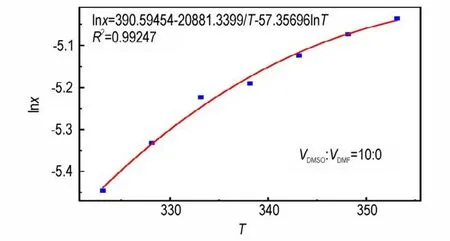
图4 Apelblat 模型对溶解度数据的拟合关系图Fig.4 Fitting relation of solubility by Apelblat model

同理，根据式（3）绘制其余溶剂体系下的拟合关系图，可求得式（3）中相关参数A、B、C及相关系数R2，并由式（2）求得RMSD，各参数值见表1。由表1 可知，该模型拟合的回归结果R2均大于0.98，误差较小，精度较高。

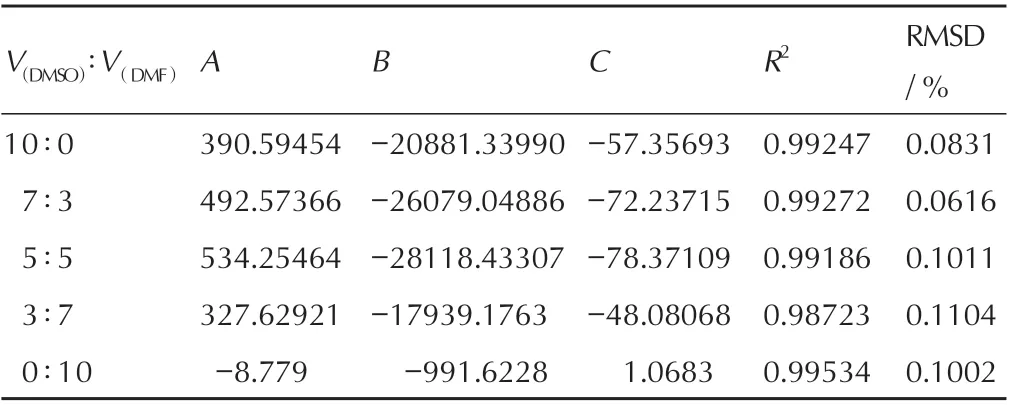
表1 5 种DMSO/DMF 溶剂体系下Apelblat 模型各参数的回归结果Table 1 Regression results of Apelblat model parameters in 5 DMSO/DMF solvent systems

采用λh模型对实验数据进行拟合关联，图5 为VDMSO∶VDMF=10∶0 溶剂体系下温度与溶解度的拟合关系。

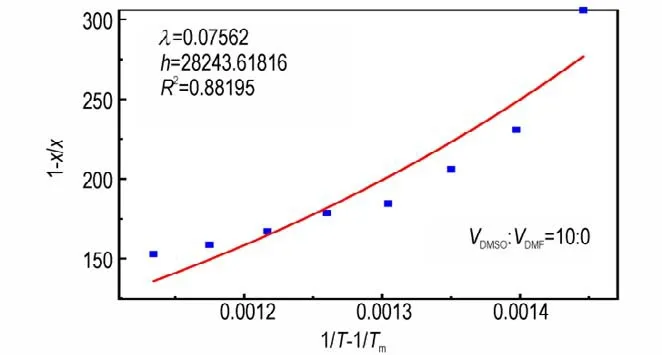
图5 λh 模型对溶解度数据的拟合关系图Fig.5 Fitting relation of solubility by λh model

同理，根据式（4）绘制其余溶剂体系下的拟合关系图，可求得式（4）中相关参数λ、h及相关系数R2，并由式（2）求得RMSD，各参数值见表2。

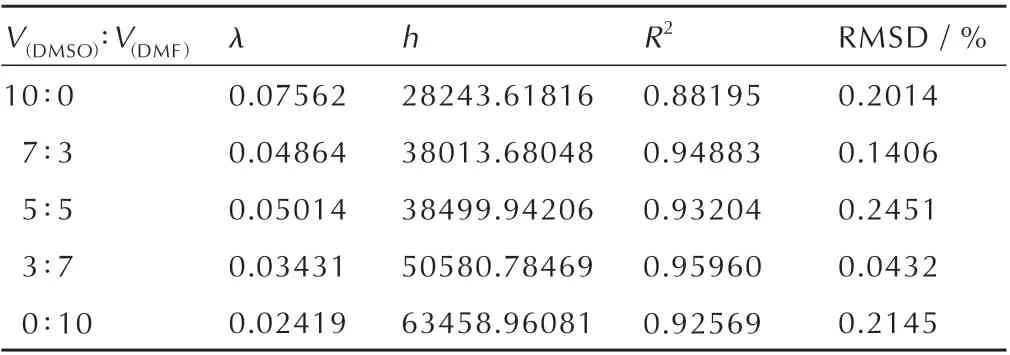
表2 5 种DMSO/DMF 溶剂体系下λh 模型各参数的回归结果Table 2 Regression results of λh model parameters in 5 DMSO/DMF solvent systems

由表1、2 中的R2与RMSD 可知，两种模型的拟合误差均较小，均方根偏差均小于0.25%，说明通过经验模型所得到的溶解度数据与测量值偏差很小，精度很高。尤其是Apelblat 模型，它能够很好地拟合出HNS在5 种溶剂体系下的溶解度，相关系数R2均大于0.98。

相较于Apelblat 模型，λh模型的R2相对偏低，由图5 可知，在温度较高的区域，拟合曲线与实验数据间的偏差变大。分析原因应该是当温度较高时，溶液温度与环境温度的差距变大，且此时的溶解度相较室温溶解度增大较多，因此溶液在通入芯片结晶腔室的过程中，由于环境温度对微管道的影响，产生少量结晶而误认为已到达平衡溶解度，以致提前停止实验，使得测量值较真实值偏小，造成实验误差。其中，对于Apelblat模型，其拟合关系图的因变量为溶解度x的自然对数，且由于x的值较小，因此即便在实验中产生少量误差，在取自然对数之后，数据间的差异并不会非常明显；而对于λh模型，其拟合关系图的因变量为（1-x）/x，测量值出现少量偏差也可对数值产生较大影响，当测量值偏小时会导致数据偏大，从而产生如图5 所示的偏差。尽管如此，该模型仍具有较好的拟合结果。

结果表明，Apelblat 模型与λh模型都可用于关联HNS 在不同DMSO/DMF 溶剂体系、不同温度下的溶解度。

3.2 溶剂体系对HNS 介稳区宽度的影响

对于炸药结晶体系而言，其结晶过程属于快速结晶，过饱和态到达晶核生成态在毫秒级尺度下完成。实验证明，当起始温度高于333.15 K 时，介稳区宽度过窄，成核时间早，难以通过激光信号捕捉到其成核时刻，数据可靠性低。因此对温度在318.15，323.15，328.15 K 和333.15 K，5 种DMSO/DMF 溶剂体系下的HNS 饱和溶液介稳区宽度进行了测定。配制不同饱和浓度的HNS 溶液，将注射泵流速固定为0.5 mL·min-1，利用测试系统进行了4 种温度、5 种溶剂体系下的20 组实验。图6 为实验温度333.15 K 时，结晶过程中激光能量与时间之间的关系。当温度达到析晶点时，激光能量出现衰减，图6 中出射能量的拐点即为析晶时刻。该时刻的温度即为析晶点温度，起始实验温度与该温度的差值为结晶介稳区宽度。

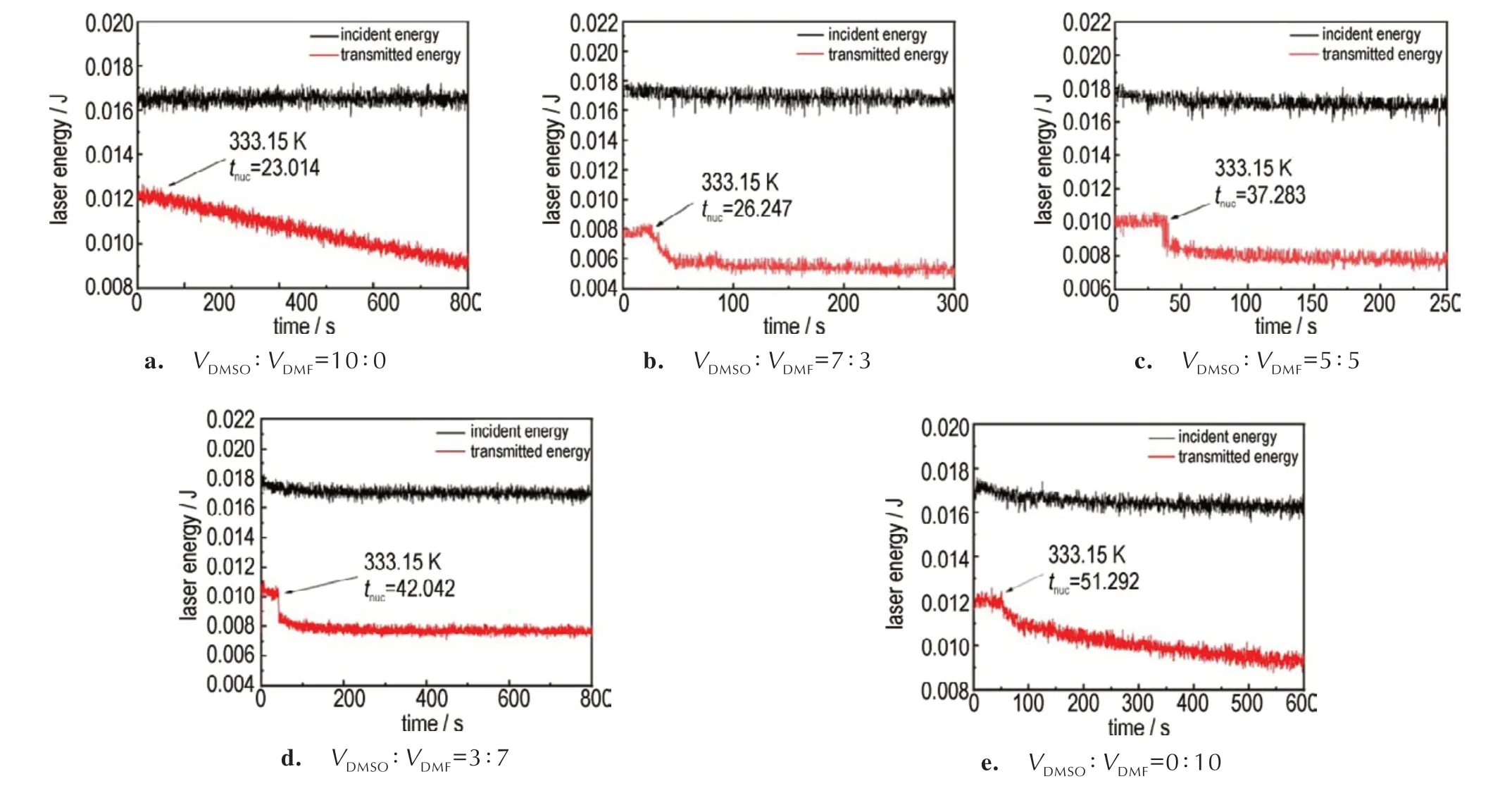
图6 333.15 K 下5 种DMSO/DMF 溶剂体系的HNS 析晶点时刻图Fig.6 Time chart of nucleation point of HNS in 5 DMSO/DMF solvent systems at 333.15 K

根据20 组实验的激光能量数据，可得到HNS 在5种DMSO/DMF 溶剂体系下的介稳区宽度，结果如图7所示。由图7 可知，在温度一定时，介稳区宽度随着溶剂中DMSO 含量的增加而变窄。这是因为随着DMSO 体积比例的增加，HNS 在混合溶剂中的溶解度增大，导致在同一结晶区域内的分子数量增加，从而增大了分子间碰撞的概率，晶核形成的可能性增大，介稳区变窄；在溶剂体系一定时，介稳区宽度随着温度的升高而变窄。这是因为随着温度的升高，溶解度增大且溶质分子的热运动加快，使得溶质分子间的碰撞几率增加，形成晶核的时间提前，介稳区变窄。

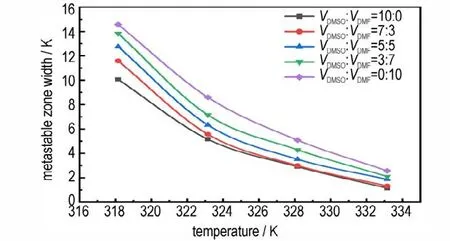
图7 不同DMSO/DMF 溶剂体系下HNS 的介稳区宽度Fig.7 Metastable zone width of HNS in different DMSO/DMF solvent systems

HNS 的晶体质量评价体系中认为粒径越小，粒径分布越窄且晶形完整无缺陷的HNS 更适合于应用。对于HNS 这种纳米级晶粒的生长而言，成核过程可近似为均相成核。因此，想要制备大量尺寸均一的纳米颗粒，就需要在尽可能短的时间内以爆发方式成核，降低成核所需克服的能量，使成核相对容易。而介稳区变窄能够缩短成核时间，增加成核数量，从而得到粒径分布窄的纳米颗粒。因此在筛选结晶条件时，认为以纯DMSO 作为溶剂，溶液温度设置为333.15 K，溶质浓度为0.029 g·mL-1为最佳结晶参数。

3.3 HNS 降温结晶成核机理分析

基于经典成核理论与自洽Nývlt 介稳区方程［28］可以对HNS 的表观成核级数与成核速率进行求解并依此分析HNS 的降温结晶成核机理。

Sangwal 介稳区方程［29］定义了成核常数K，并采用幂函数的形式将介稳区边界附近的成核速率J表示为：

式中，x为溶质溶解度的摩尔分数；ΔS是溶解熵，J·mol-1·K-1。

同时该介稳区方程假设在介稳区附近成核速率J与相对过饱和度的变化率成正比，则成核速率J表示为：

式中，ΔTmax为极限过冷度，即介稳区宽度，K。通过对注射泵流速的设置，获得降温速率为12，24，48，72，108 K·h-1的介稳区数据，根据式（9）可以得到ln（ΔTmax/T0）与lnR的线性关系，如图8 所示。

根据图8 中直线的斜率和截距结合公式（9）可得成核级数m与成核常数K，相关动力学参数如表3所示。

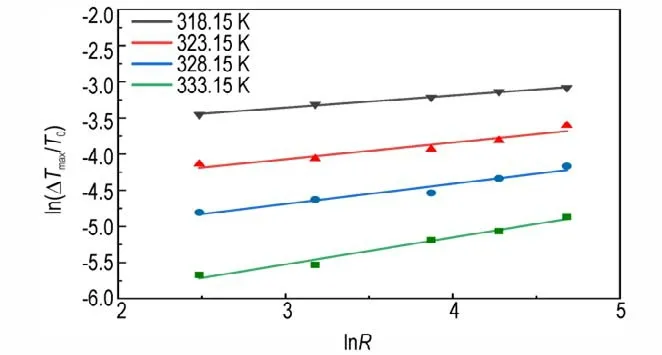
图8 HNS 在DMSO 中ln（ΔTmax/T0）与lnR 的关系Fig.8 The relation between ln（ΔTmax/T0）and lnR of HNS in DMSO

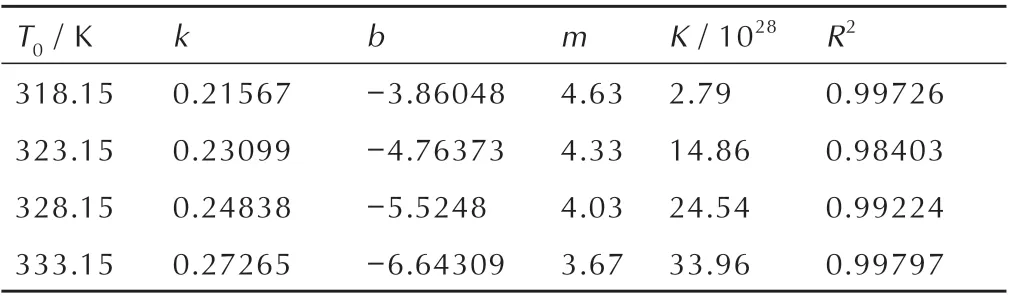
表3 HNS 的成核动力学参数Table 3 Nucleation kinetics parameters of HNS

从表3 中可以看出成核级数与起始温度间的关系并不大，m的值大约在4 左右。表观成核级数m的大小代表了溶质与溶剂间的相互作用力大小，m越小，相互作用力越强，更有利于溶质在溶剂中扩散，使生长单元聚集，能够形成稳定晶核的能力越强。这有利于增强扩散过程，扩散控制生长机制符合均相形核方式，有利于生成尺寸一致的颗粒。根据先前的文献，Kashchiev 等［30］提出，表观成核级数m＞3 时，控制成核的主导机理为连续成核，这意味着在高于318.15 K时，在DMSO 溶剂中HNS 是以爆发式成核作为主导成核方式的。与此同时，从成核常数K的数据可以看出，随着起始温度的升高，单位时间体积内的晶核数目也随之升高，这与3.2 节得到的结论相一致。