数值集合降雨预测的校正后处理方法研究
2022-05-19郝福亮
郝福亮, 王 旭
(1.长沙理工大学 水利与环境工程学院, 湖南 长沙 410114; 2.水沙科学与水灾害防治湖南省重点实验室,湖南 长沙 410114; 3.天津大学 环境科学与工程学院, 天津 300072)
1 研究背景
数值模式降雨预测在暴雨预警、水库调度、径流预测等实际应用中发挥着重要作用,但传统确定性预测经常受到系统模式无法完全模拟大气过程和初始场资料观测误差的影响[1],导致确定性预测的结果表现出较大的不确定性,很难帮助用户做出正确的判断。为解决单一确定性预测的结果不确定性问题,近年来降雨预测的模式从确定性预测转向多成员集合预测,通过初值扰动和模式扰动的方式来描述初始场和模式自身的不确定性,并使用扰动后的数据制作一系列的预测结果,以集合的形式来描述未来降雨可能会发生的概率情况[2]。但由于大气系统的高度非线性、数值预测系统的系统性误差、初始条件的同化及扰动方法不完善等因素导致了数值集合预测产品存在预测误差以及集合成员间存在低离散度的问题[3-4],因此集合预测产品无法直接被使用,必须使用校正后处理方法对其进行有效地处理后才能为用户提供更多的有效信息。
国外学者较早地认识到校正后处理方法对降雨等气象数值预测的重要性,开发出的校正后处理方法在数值预测中得到广泛应用[5-8]。目前校正后处理方法主要可以分为非参数化后处理方法和参数化后处理方法[9]。非参数化后处理方法主要有频率匹配法[10]、集合伪偏差校正[11]等,其原理较为简单,不需要提前考虑分布函数模型的问题,在使用中相对灵活,但校正处理时需要大量的数据样本,限制了其在数据缺乏区域的使用。以贝叶斯模型平均法为代表的参数化后处理方法通过假定预测成员满足特定连续概率分布,并且可以利用该分布模型完成数据外插[9],在很大程度上减少了对数据样本的需求量。另外非参数化后处理方法往往不能对降雨预测进行全面的校正,例如Zhao等[12]在评估分位数映射方法对季节性降雨预测的校正性能中发现,分位数映射虽然可以校正预测偏差,但往往会表现出负向的预测技巧性,而参数化后处理方法贝叶斯联合概率建模[13-14]则表现出较为全面的校正效果。2005年Gneiting等[15]在模式输出统计的基础上提出非常有代表性的参数化后处理方法框架 - 集合模式输出统计(ensemble model output statistics,EMOS),该方法首先给定所需预测天气变量的概率分布,然后利用函数将预测分布的参数与预测成员相连接,并通过优化算法求解出模型参数来实现预测校正[16],例如原始的EMOS方法使用高斯分布对温度和海平面压力进行建模,高斯分布的均值是预测成员的映射函数,其方差是集合方差的映射函数。该方法在概念上相较于目前非常流行的贝叶斯模型平均法更加简单清晰,对于数据样本的要求量较贝叶斯模型平均法也要少很多,因此在使用中会更加灵活方便[17]。
为能够使用EMOS方法对截断变量和非高斯变量进行建模,近十年中陆续在原始EMOS方法的基础上发展出多个统计模型。例如针对降雨预测的后处理,建立了基于左删失广义极值分布的EMOS模型[18]。该模型在德国地区降雨预测校正中有着较为出色的表现,但由于开发时间较短,在降雨校正中的应用效果并未得到充分验证,特别是针对中国地区的适用性还很少被探讨。因此本文以雅砻江流域为研究对象,使用该方法对流域内的降雨预测进行校正处理,并分析讨论了经该方法校正后的预测结果与原始预测结果之间的差异。
2 数据来源与研究方法
2.1 研究区概况
雅砻江流域位于青藏高原东侧,地处东经96°52′ ~ 102°48′,北纬26°32′ ~ 33°58′,整个流域呈条状分布由南至北跨越近8个纬度带,流域面积约13.6×104km2,干流总长度达1 323 km,流域水系、高程及气象站点分布情况如图1所示。
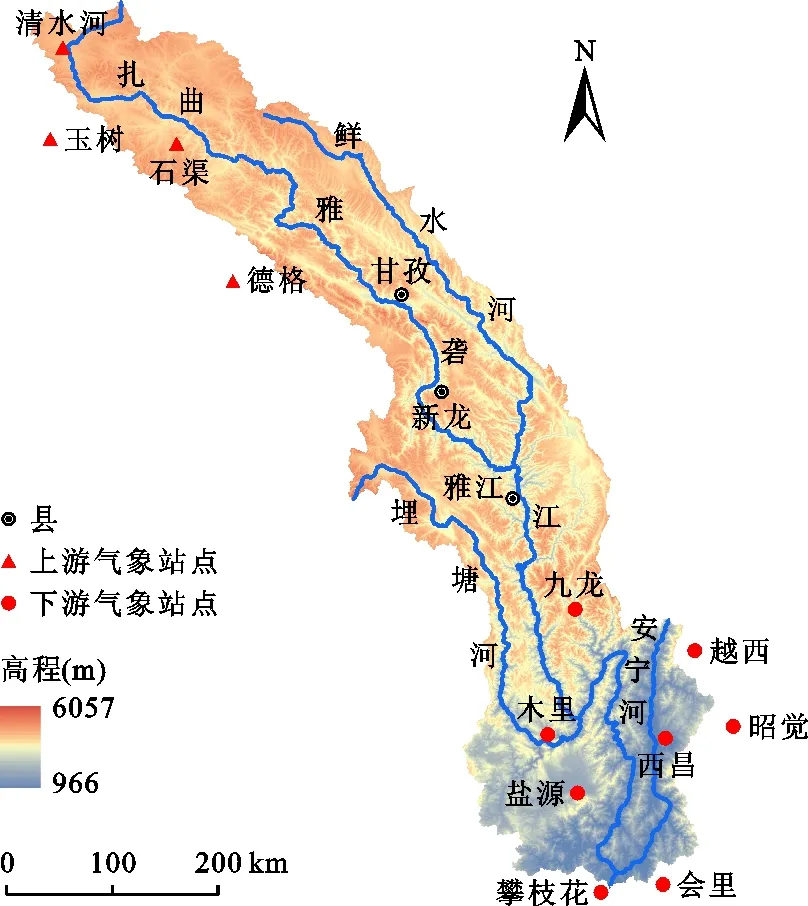
图1 雅砻江流域水系、高程及气象站点分布
流域内地形复杂,谷岭高差悬殊,海拔高度多在1 500 m 以上,气候在不同的地区和高程均有较为明显的差异。流域每年雨季(6-9月)受到西太平洋副高脊线北移以及西南季风携带大量暖湿水汽的影响,流域内切变线和低涡频繁活动导致该时期时常会有暴雨、山洪等灾害发生[19-20],支流鲜水河、安宁河为流域重要的产洪区。在流域的中下游一带水汽较为丰沛,暴雨量级很大,对流域内居民的生产和生活造成威胁。流域内复杂的地形和恶劣的地理环境导致水文和气象监测站点分布十分不均匀,特别是甘孜以上的流域站点分布稀疏、数量少,为当地水利管理人员进行水库调度和发电计划制定增加了很大的难度,因此通过适当的校正后处理方法对数值模式的降雨集合产品进行校正,并将校正后数据应用到流域实际生产中对于雅砻江流域有着非常重要的意义。
2.2 数据来源
降雨集合预测数据来自全球集合预测系统(Global Ensemble Forecast System, GEFS),数据分辨率为高斯网格0.5°[21]。该系统在世界协调时00时发布未来16 d内的降雨预测数据,集合成员为11个,在本次研究中选用2017年4月1日-9月30日时段内24 h累计降雨预测数据。降雨观测资料来自雅砻江流域12个气象站点,时效为北京时间20时至次日20时,共24 h累计降雨数据。预测数据集在世界协调时00时初始化,而观测数据为北京时间20时至次日20时累计降雨量,导致预测数据的起报时间与降雨观测数据开始累计时间相差12 h,因此在整合每日降雨预测数据时将开始时间向后推移12 h,从而使降雨预测数据与观测数据在时间上是一致的。
2.3 研究方法
基于左删失广义极值分布的EMOS模型使用广义极值分布取代了EMOS模型中的正态分布,并认为广义极值分布在零处是左删失的,即分布中低于零的位置被精确地赋值为零,因此方法中所采用的分布函数G(y)如下:
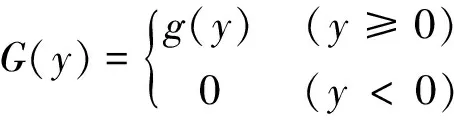
(1)
式中:g(y)为广义极值分布。
确定出分布函数后便需要将其参数与合适的预测变量进行连接,如公式(2)、(3)所示。广义极值分布的平均值与预测变量之间有两种方式建立关系,可以通过为集合成员赋予不同权重来构建函数关系,另外也可以通过使用集合均值来构建函数关系。同时广义极值分布的比例参数σ和集合成员的平均差MD(X)之间也可以通过一次函数构建联系,如公式(4)所示。
m=a+b1X1+…+bnXn+sp0
(2)
(3)
σ=c+d·MD(X)
(4)
式中:m为广义极值分布的平均值参数;p0为集合成员中0值占集合总数的比例;各项系数a、b、c、d、s可以通过拟牛顿算法进行优化求解,待模型参数确定后,便可以利用该模型完成统计校正工作。
平均值与预测变量之间构建关系的方式在一定程度上会对模型校正效果产生影响,但目前关于上文中提到的两种建模形式在不同的数值预报系统及地区中的表现并未进行深入探讨。因此在本项研究中笔者选取国内的雅砻江流域作为研究区域,利用基于左删失广义极值分布的EMOS模型对数值预报中心发布的该地区降雨预测数据进行校正处理,并讨论该方法的两种建模形式在校正中的差异。本次实验分别在雅砻江流域的上游和下游区域选取部分气象站点作为实验对象,通过在流域不同区域下分别采用基于左删失广义极值分布的EMOS模型的两种建模形式对降雨预测进行校正,并对两种形式校正后的结果进行对比分析。
由于建模过程中所采用的数值预测数据是全球网格形式的数据,因此预测数据与气象站点的观测数据在空间位置上并没有完全对应,为解决该问题,在数据处理中首先从数值预测数据中确定出距离每个气象站点位置最近的4个格点位置,然后对4个位置上的数据进行平均作为本次实验的预测数据。另外基于左删失广义极值分布的EMOS模型通常使用校正日期前几十天的数据作为模型参数训练数据集,虽然采用更多的训练数据可以获得更加稳定的参数估计,但降雨数据季节性变化可能会对模型校正产生较大影响,因此训练长度普遍在30~60 d之间。在此次实验中整理了2017年4-9月每一天的降雨预测和降雨观测数据集,并针对模型训练日期长度对预测结果的影响进行预实验,最终确定选取43 d作为本次实验的最终训练长度。针对雅砻江流域站点降雨预测,分别采用上述方法的两种建模形式进行了校正处理工作,并通过计算相应的评价指标对其结果进行了评价。在下文中为方便对结果进行讨论,将集合成员赋予不同权重进行校正的形式简称为集合预测,将使用集合均值进行校正的形式简称为均值预测。
平均绝对误差(mean absolute error,MAE)为各预测值与实际观测值偏差绝对值的平均值,是一种较为直观的确定性评价指标,在气象水文等领域被广泛采用。
(5)
式中:N为样本数;fi为预测值;xi为与预测值对应的观测值。MAE值越小,表示预测值与观测值之间的误差越小,预测能力越强。
连续排名概率得分(continuous ranked probability score,CRPS)用于衡量预测的累计分布函数与确定性观测样本(真实值)之间的差异。
(6)
式中:y为预测变量;F为预测累计分布函数;H为阶跃函数,预测变量小于观测值时其值为0,大于观测值时为1;yobs为实际观测值。完美预测的CRPS值等于0,且该值越大,集合预测系统的预测能力越弱。
3 结果与分析
本节中通过计算平均绝对误差、连续排名概率得分等指标对原始预测、均值预测、集合预测的预测准确性进行了对比分析,并进一步讨论了均值预测在流域不同区域的校正效果。
3.1 预测分位数区间与观测值对比
通过绘制预测区间与观测值的对比情况可以直观评价预测效果,图2为雅砻江下游盐源站122 d的10%~90%预测区间与观测值的对比情况。由图2可以看出,原始预测中大部分的观测值落在预测分位数区间之外,预测分位数区间仅能覆盖到10~30 mm降雨量中的很少一部分值,对于大于30 mm和接近0的降雨量值则很难捕捉到(图2(a))。另外在原始预测中大部分观测值低于预测的下四分位数,即原始预测在预测中表现出对降雨量过高的估计,这是目前大多数数值集合预测系统存在的问题。均值预测纠正了原始预测结果偏高的问题,可以覆盖到更多的观测值(图2(b)),但是集合预测的结果表现并不理想,在对原始预测结果偏高的问题上表现的过于偏激,很多时候出现预测集合成员均为零值的情况,导致集合预测的预测区间无法有效覆盖观测值(图2(c))。
图3为雅砻江上游清水河站122 d的10%~90%预测区间与观测值的对比情况。由图3可以看出,原始预测出现和下游站点同样的问题,预测集合区间无法覆盖到较小的降雨量,过高估计了2 mm以下的降雨量。均值预测和集合预测明显改善了原始预测高估降雨量的问题,特别是均值预测使绝大部分的观测值落入到预测区间内。
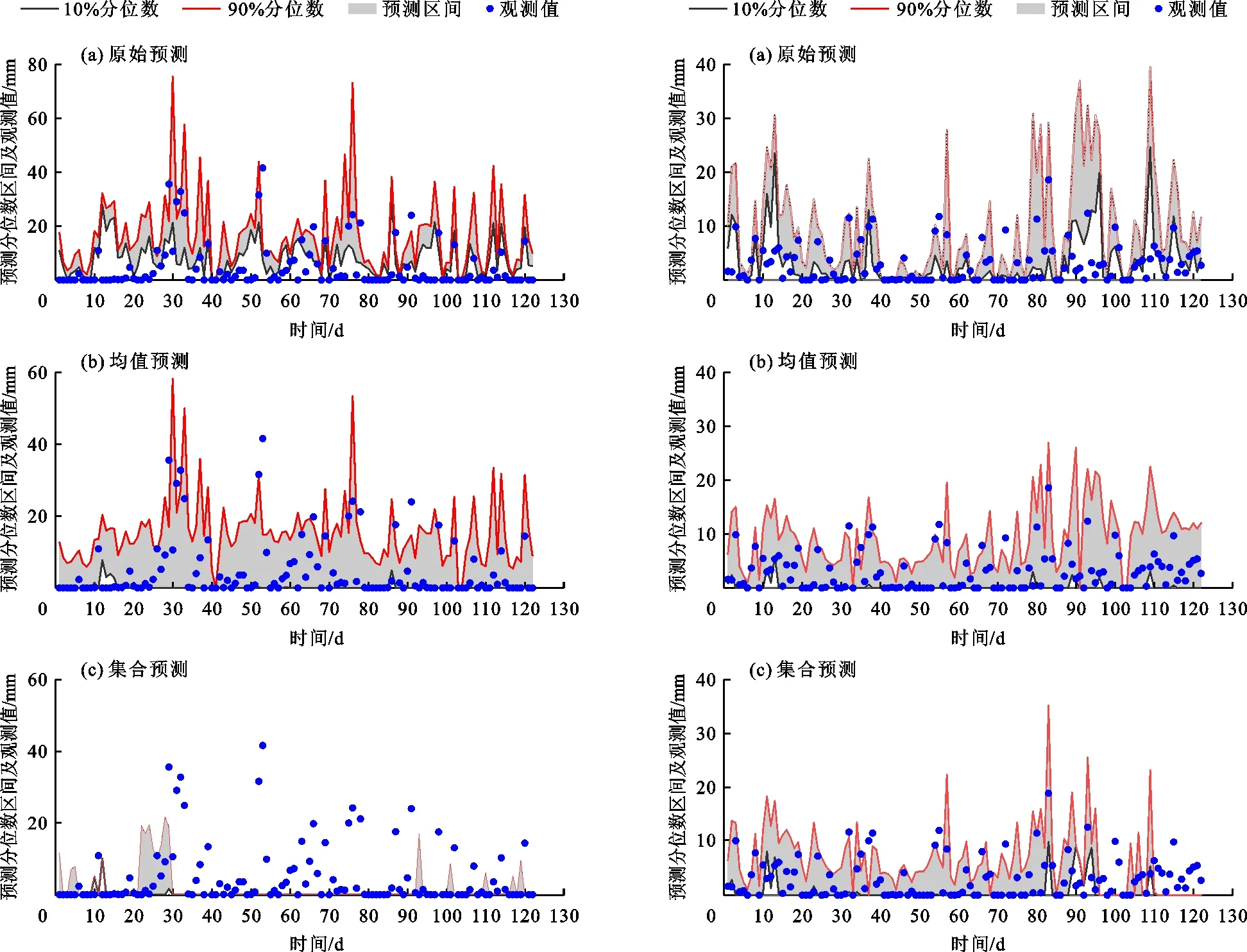
图2 雅砻江流域下游盐源站降雨量122 d预见期下10%~90%预测区间与观测值对比 图3 雅砻江流域上游清水河站降雨量122 d预见期下10%~90%预测区间与观测值对比
通过分析两种建模方式预测区间与观测值的对比情况可以发现均值预测可以达到更好的校正效果。虽然集合预测通过为集合成员赋予不同权重的方式考虑到集合成员对预测结果的不同贡献,但并没有使得预测结果有所提升,反而出现过度校正的问题,特别是下游区域中出现了多次预测区间为零的情况,这样的问题虽然在上游区域内得到改善,但通过图3可以发现集合预测在最后几天预测中依然存在预测区间为零的情况。
3.2 平均绝对误差
图4为雅砻江流域上游和下游区域降雨量在不同预见期下平均绝对误差值的对比情况。由图4可以看出,均值预测和集合预测的平均绝对误差相较于原始预测均有所减小,两种形式的校正方法在大部分情况下能够使平均绝对误差减小20.0%以上,说明基于广义极值分布的EMOS方法可以在一定程度上提高原始预测的准确性;均值预测和集合预测的MAE值在不同区域下具有差异性,均值预测在上游地区的MAE值要明显优于集合预测(图4(a)),均值预测的MAE值相较于集合预测能够减小5.0%以上,特别是在第5、6 d的MAE值分别减小了11.4%和10.0%。但在下游地区均值预测的MAE值并没有明显优势,仅在第4和6 d均值预测的MAE值相较于集合预测减小了22.7%和6.6%,其他情况下则是集合预测的MAE值更小(图4(b))。根据3.1节中预测区间与观测值对比分析的结果可知,集合预测在下游站点中的预测效果并不理想,但此时集合预测的MAE值在更多情况下表现得更小,显示出更高的预测准确性,这一点需要从指标本身进行一定的分析。图2表明,观测降雨量为0或接近0的天数占到了很大的比重,此时集合预测将多数情况下的集合成员全部预测为0,使得预测集合的均值在更多的时候更加接近观测值,即使在个别日期下预测集合的均值与观测值之间有较大的差异,但由于所占比重有限,当对所有预测天数取平均计算MAE值时,在平均过程中很容易去除掉一些较大预测偏差对整体计算结果的影响,从而导致对预测结果的评判错误。
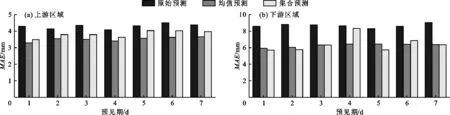
图4 雅砻江流域上、下游区域降雨量在不同预见期下的MAE值
3.3 连续排名概率得分
图5为雅砻江流域上、下游区域降雨量在不同预见期下连续排名概率得分的对比情况。由图5可见,均值预测的预测结果拥有明显优势,上游的CRPS值相较于原始预测减小了15.0%以上,下游的CRPS值减小可以达到30.0%以上,均值校正的方式有效改善了集合成员与实际观测值之间误差过大的问题,使得预测结果更加准确、可靠。集合预测的CRPS值则并不理想,在某些情况下大于原始预测的CRPS值,这说明集合预测使得集合成员与实际观测值之间的误差变得更大。通过对比图4(b)和5(b)可以发现,MAE值与CRPS值对于均值预测和集合预测的评价结果并不完全一致,均值预测的MAE值除在第4和6 d预见期下分别比集合预测小1.89、0.45之外,在其他预见期下均略大于集合预测的MAE值,但CRPS值则呈现出不同的评价结果,在不同预见期下集合预测的CRPS值明显要比均值预测更大。对于MAE值和CRPS值在均值预测和集合预测中评价结果不一致的问题进行进一步探究,发现MAE值为预测与观测值之间差值的一次函数,该评价指标对于极大偏差值并不敏感,但CRPS值为预测与观测值之间差值的平方项指标,相较于MAE值对于预测中一些极大偏差值的影响会更加敏感,因此导致了MAE值与CRPS值两指标评价结果的差异。
3.4 均值预测在不同区域下的对比
图6为均值预测的MAE值和CRPS值在雅砻江流域上、下游区域的差异情况。由图6可以发现,上游区域的MAE值和CRPS值相较于下游相应值要小40.0%以上;在不同预见期下评分的表现较为一致,随着预见期的增加,预测的评价值会有一定程度的增大,第7 d预见期的评价值相较于第1 d的评价值大致提高了7.0%~11.2%。
上游区域和下游区域的评价值出现较大差异主要是由极值预测结果的准确性引起的,下游区域在雨季时受到季风气候的影响水汽充足,时常会有较大降雨量出现,上游区域的水汽相对于下游少很多,较大降雨量出现的可能性也较小,这一点通过图2与3的对比可以很好的说明,下游盐源站20 mm以上的降雨量天数可以占到2017年所有预测天数的9.0%,但上游清水河站则仅出现一天接近20 mm的降雨量。均值预测在下游站点中很难对较大雨量做出准确的预测,往往倾向于过低地估计较大雨量,但是在上游地区这样的大雨量很少发生,因而对上游地区降雨预测的不确定性要远小于下游地区,所以此时均值预测能够对绝大部分观测值做出准确的预测。
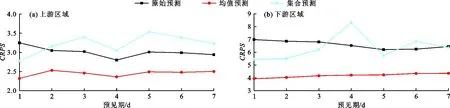
图5 雅砻江流域上、下游区域降雨量在不同预见期下的CRPS值
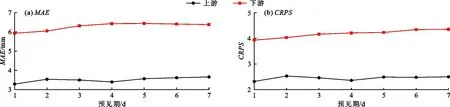
图6 均值预测的MAE值和CRPS值在雅砻江流域上、下游区域的差异
4 讨 论
(1)实验结果表明,基于左删失广义极值分布的EMOS模型能够在一定程度上改善雅砻江站点降雨的预测性能,但采用为集合成员赋予不同权重的建模形式并没能达到预期效果,特别是在下游区域中出现多次预测集合为0的情况。集合预测中由于模型参数增加导致该方法在校正处理中出现过度拟合的问题,因此采用为集合成员赋予不同权重的建模形式并不适用于本次数值集合预测的校正处理,但这并不意味该建模形式没有应用价值,Scheuerer[18]曾在文章中指出,如果一个集合预报中一些成员的预报技能明显低于其他成员时,该方式所付出过度拟合的代价是值得的。因此在接下来的研究中需要选取多种数值预报中心的集合预报对该建模形式进行更加充分的验证。
(2)基于左删失广义极值分布的EMOS方法在进行参数求解时为了能够获取足够多的数据进行参数估计,便将预测区域内所有站点前期数据用于计算,导致所有站点均采用同一套模型参数,而没有考虑参数在空间上的差异性,这在一定程度上也会对不同区域下的校正结果产生影响。如在本次实验中雅砻江流域下游区域的水汽较为充足,降雨量在空间上会有较大的变化差异,当每一个站点使用相同的模型参数时,则降雨量在空间上的变化差异无法得到体现,数据平均过程使得模型无法对极值降雨量进行准确预测,相反,上游水汽相对较少,降雨量在空间上的差异小于下游,因此上游区域降水预测受到参数一致性的影响较小。在接下来的研究中需要进一步明确降水量的空间差异性对该方法的校正效果究竟会产生多大的影响,并在此基础上对方法进行改进。
5 结 论
本研究将基于左删失广义极值分布的EMOS方法应用到雅砻江流域降雨预测的校正后处理中,实现对降雨预测的校正工作。通过分析对比均值预测和集合预测对降雨预测校正效果的差异,可以得到如下主要结论:
(1)基于左删失广义极值分布的EMOS模型采用集合成员作为分布参数预测因子时其预测校正结果并没有达到预期效果。该方式因在模型构建中为模型赋予过多的参数,使得模型变得更加复杂,导致模型极易发生过度拟合的问题,无法对降水预测进行有效的校正。
(2)基于左删失广义极值分布的EMOS模型采用集合预测均值作为分布参数预测因子时预测结果准确性相比原始预测得到较大提升,其预测结果明显优于采用集合成员作为分布参数预测因子方式的预测结果。但该方式的预报结果依然存在漏报问题,特别是针对流域中较大量级降雨的预测不准确。
(3)采用集合预测均值作为分布参数预测因子的方式无法对较大量级降雨进行准确预测的问题导致该方式预测结果的准确性在流域不同区域出现较大差异,由于下游区域的水汽充沛,发生大量级降雨的次数明显大于上游,因此其预测结果在上游的准确性比下游更高。
