基于TF-熵权法的矿井通风系统可靠性可拓评价*
2022-05-19邵良杉张佳琦于保才白廷海
邵良杉,张佳琦,于保才,白廷海
(1.辽宁工程技术大学 系统工程研究所,辽宁 葫芦岛 125105;2.中煤华晋集团有限公司,山西 太原 043300)
0 引言
现今,煤炭仍然在我国能源消耗中占主要地位,在2019年国家统计局发布的统计公报中显示[1],全年煤炭消费总量28.04亿t,占能源消费总量的57.7%,原煤产量为38.5亿t,比上年增长4.0%。然而,煤矿事故时有发生,严重影响着矿工的人身安全、企业的持续经营以及国家的财产安全,根据国家煤矿安全监察局会议报告[2],在2019年发生的170起安全事故中,死亡人数约为316人,其中因通风系统故障而导致的事故占比不小。因此,为提高矿井作业的安全可靠性,减少事故发生,有必要对矿井通风系统可靠性进行深入研究。
近年来,国内外许多专家学者对矿井通风系统可靠性评价做了大量研究,伴随着矿井通风系统的改进与发展,研究工作也有了一定的进展。Frycz 等[3]采用通风系统运行可靠度的计算方法对矿井通风系统的可靠性进行了判断;Rezaei等[4]以巷道阻力和各支路流量变化作为可靠性指标和标准,提出了1种基于割集法的煤矿井下网络可靠性逐步评价方法;Jiang等[5]基于矿井通风系统评价体系中的不确定信息,建立了未确知测度函数向量模型,得到了较为精确的结果。在国内,陈开岩等[6]应用多层次模糊评价法进行模糊综合评价算法开发,提出了更加快速合理的通风系统可靠性评价方法;王洪德等[7]提出了基于粗糙集-神经网络的通风系统可靠性评价方法,从全新角度构建指标体系,使评价过程更快;史秀志等[8]将Fisher判别分析理论应用到通风系统可靠性评价中,建立了矿井通风系统安全可靠性的Fisher判别分析(FDA)模型。
上述研究方法各有优势,但也各有局限,如专家评价使评价结果有一定的主观性,语言变量指标的权重确定和可靠性等级判定不够准确。在以往的研究中,通常选用熵权与物元可拓法结合来减少主观性带来的误差,例如刘兵等[9]提出将熵权物元可拓模型用于城市轨道交通线路运营风险评价中,但是在有效的解决权重与等级可靠性主观性问题的同时也失去了语言变量的弹性与准确性,因此,为解决此问题,本文将三角模糊数与熵权结合,引入物元可拓模型,提出基于三角模糊数与熵权法组合的物元可拓模型,对矿井通风系统的可靠性进行可拓性评价研究,并且也为矿井通风系统可靠性评价研究提供新思路。
1 确定矿井通风系统可靠性评价指标体系
通过矿井通风系统可靠性文献分析[10-11]以及矿井通风标准,初步得出影响矿井通风系统可靠性的6个2级指标,包括通风动力、通风网络、通风基础设施设备、作业环境、防灾救灾系统和人员管理因素以及29个3级指标,其中定量指标11个,语言变量指标18个。定量指标数据来源于王家岭矿井2020年7月测风旬报表以及简单公式计算得出。语言变量则利用德尔菲法通过王家岭通风科的专业工程人员形成专家组进行指标打分得来。本文根据调研目的和现场实际情况对德尔菲法进行修改,共分为专家选择、专家征询及专家意见可靠性分析与统计结果3个部分。
1)专家选择
根据研究目标和研究所需的知识范围,选择工作年限均为3 a以上的10名专业人员为专家组成员,其中5人为王家岭煤矿通风科工作人员,另外5人为生产科工作人员,由于2科室对煤矿安全与矿井通风系统可靠性重要度相同,因此,设二者比重为1∶1。
2)专家征询
本文采用现场调研的方式进行专家征询,并对征询结果进行可靠性分析。首先,向专家组提供矿井通风系统可靠性评价研究的目的、研究背景以及拟定的指标体系,专家对王家岭煤矿指标的熟悉程度、实践经验、理论程度和指标重要性进行评价,根据可靠性分析结果决定是否确定矿井通风系统可靠性评价指标体系,否则,再进行多次指标筛选;其次,专家组需对王家岭通风系统语言变量指标现状进行打分;最后,进行指标间的相对重要度比较,进行主观权重计算。评价结果以及主观权重见表1。
3)专家意见可靠性分析与统计结果
专家意见可靠性分析意在分析专家组专业程度与评分可靠度,是衡量最终评分结果是否准确可靠的重要环节,主要从专家的积极系数、专家意见的集中程度、专家意见的变异系数和专家意见的权威程度4个方面进行分析与考核指标筛选[12]。
依据调研数据分析以及专家意见可靠性[13],确定考核指标筛选标准为:当专家权威系数≥0.7、指标重要性赋分均值>3.5、变异系数<0.3,则指标保留,无需修改,否则再次进行指标修改与征询。由于调研前期指标选择工作准备较充分,第1轮征询的专家权威系数为0.72,重要性赋分均数为4.37,最大值为4.7,最小值为3.9,专家意见变异系数在0.1~0.27之间,以上各项均在合理范围内,再结合100%的专家积极系数,所以保留第1轮各项指标作为最终的通风系统可靠性评价指标,无需评价指标修改。通风系统可靠性指标体系见表1。

表1 矿井通风系统评价指标体系
2 基于三角模糊数-熵权法的物元可拓模型可靠性评价过程
2.1 确定矿井通风系统可靠性评价指标权重
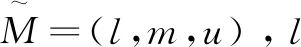
2.1.1 利用三角模糊数初步确定权重
对中值矩阵进行一致性检验。计算中值矩阵M=(mij)n×n,计算其最大特征值λmax,依照传统的AHP方法,进行一致性检验,若检验结果显示CR<0.1,则一致,并继续计算,否则根据一致性调整新方法[14],调整为一致。CI,CR计算分别如式(1)和式(2)。
(1)
CR=CI/RI
(2)
式中:RI为随机性指标;n为矩阵阶数。
构建模糊评判因子矩阵E=(eij)n×n。eij,dij计算分别如式(3)和式(4)。
(3)
(4)
式中:eij表示第i个指标相对于j指标的模糊重要程度;lij为元素aij闭区间下限;mij为中值;uij为上限。
计算调整矩阵Q如式(5)。
(5)
式中:E为模糊评判因子矩阵;M为中值矩阵;m为最优值。
根据矩阵Q,利用Matlab(R2016b)计算各项指标的权重si。
2.1.2 综合熵权法确定最终权重
(6)


(7)

(8)
(9)
式中:β为乐观指标系数,表示对指标相对重要度判断的满意程度。β的值越大,表示对判断结果越有把握;l为模糊矩阵闭区间下限;m为中值;u为上限。
根据熵权法的计算公式,可求得各个指标的熵权fi。
最后,将2级指标权重与3级指标权重综合,并利用加权平均法进行耦合处理,得到最终的指标体系权重,计算如式(10)~(11)。
(10)
(11)
式中:Wi为最终综合权重;(si)3级为三角模糊法求得的3级指标权重;(si)2级为三角模糊法求得的2级指标权重;(fi)3级为熵权法求得的3级指标权重;(fi)2级为熵权法求得的2级指标权重;i为指标序数。
2.2 确定矿井通风系统可靠性评价等级
可拓理论是20世纪80年代初由蔡文教授提出的,运用可拓学的基本理论,从定性和定量2个角度,利用物元的可拓性确定定性计算,利用可拓集合论的关联函数进行定量计算,通过建立物元模型将各个评价指标转化为一种相容的问题,然后进行评价,得到等级关联度,进而确定评价等级[16-18]。
1)确定矿井通风系统可靠性评价指标经典域及节域,计算如式(12)~(13)。

(12)
式中:Nj为矿井通风可靠性评价指标的第j个评价等级,j=1,2,3,4,5;ci为第i个矿井通风可靠性评价指标;Vji为ci在第j个评价等级的区间量值,即经典域,其中ajn为等级区间下限;bjn为等级区间上限。

(13)
式中:p为矿井通风可靠性评价指标的全部等级;Vpi为第i个指标ci在全部等级的区间量值,即p的节域。
2)确定矿井通风系统可靠性评价的待评价物元。
根据确定的指标等级及参评人员给出的评价对象P0在评价指标ci下所取得的量值,对矿井通风可靠性评价等级隶属区间进行确认,用待评物元Q0来表示,如式(14):
(14)
3)确定矿井通风系统可靠性评价指标关联度。
首先,定义ρ(vi,Vji)为待评物元在各评价指标下的分值vi与各评价指标规定的取值范围Vji的距离,计算如式(15):
ρ(vi,Vji)=|vi-(aji+bji)/2|-(bji-aji)/2
(15)
其次,关联函数表示当物元的量值取为实轴上的一点时物元符合所要求的取值范围的程度,则矿井通风可靠性评价指标关联函数定义如式(16):

(16)
式中:Kj(vi)为vi的关联函数;ρ(vi,Vpi)的定义同ρ(vi,Vji)。
4)计算矿井通风系统可靠性评价综合关联度,计算如式(17):
(17)
式中:Wi为由式(11)确定的矿井通风可靠性评价指标权重;Kj(P0)为待评对象P0属于第j级的综合关联度。
5)确定矿井通风系统可靠性综合等级。
若Kj=max{Kj(P0)}(j=1,2,…,m),则待评对象P0的通风可靠性等级为j级。
3 王家岭煤矿通风系统可靠性评价
3.1 王家岭煤矿矿井概况
王家岭煤矿位于山西省乡宁县西南部,南距河津市约20 km,西距西安市283 km。井田东北向长约20.8 km,西南向宽约5.8 km,面积119.710 9 km2。井田设计生产能力约6.0 Mt/a,自燃倾向性等级为Ⅲ级、不易自燃,但具有煤尘爆炸危险性。井下通风系统采用中央分列抽出式通风,为三进一回式,为了响应政策,保证井下作业安全,经过3 a王家岭煤矿实现了“一通三防”自动化、信息化协同管理。通风系统可靠性评价过程如下。
3.2 数据获取
1)王家岭煤矿待评物元对应分数来源
待评物元评价对应分数即指标评价分数,是通风系统可靠性评价的关键,本文的定量指标原数据源于王家岭煤矿7月测风旬报表,并对其进行了归一化处理。语言变量指标来源于专家组对王家岭煤矿各项定性指标当前现状的打分结果,对10位专家组成员的评分结果进行加权平均,得到最终语言变量指标的分数结果。全部指标分数见表2。

表2 王家岭煤矿待评物元对应分数
2)指标综合权重数据来源
经过德尔菲法的专家打分与可靠性分析,确定通风系统可靠性评价指标与所有指标分数,通过专家组成员对6项2级指标以及各2级指标下属的3级指标进行指标间的重要程度进行对比,继而根据本文中所提到的求权重模型计算获得指标权重。最后根据专家科室比重以及指标层级对所得指标权重进行线性加权平均,获得最终的综合权重,见表1或表3。
3.3 矿井通风系统可靠性评价指标权重计算
根据公式(1)~(5)中三角模糊数公式确定主观权重。取水平截集为α=0.05,乐观指标β=0.5,根据公式(6)~(9),将三角模糊数判断矩阵进行转化,进而根据熵权法公式求得客观权重。根据式(10)~(11),利用加权平均法耦合处理,求得最终综合权重,各项权重数据见表1。
3.4 矿井通风系统可靠性评价等级计算
根据指标特征以及专家组分析,将矿井通风系统可靠性等级分为5个等级,即可靠Ⅰ、较为可靠Ⅱ、基本可靠Ⅲ、较不可靠Ⅳ和不可靠Ⅴ,评语等级以及指标隶属区间见表1。根据公式(12)~(13)求出王家岭煤矿通风系统可靠性评价的待评物元经典域和节域,根据公式(14)确定王家岭通风系统待评物元,根据公式(15)~(17)以及表1~2,计算出王家岭煤矿的通风系统可靠性等级的关联度,见表3。
表3中,可看出王家岭煤矿通风系统整体可靠性等级为Ⅰ级,其中主通风机运行稳定性、主通风机综合效率以及局部风机运行合理性等16项指标的可靠性等级为Ⅰ级,即可靠。有效风量率、通风阻力分布可靠度以及矿井总进风量比等13项指标的可靠性等级为Ⅱ级,即较为可靠。该矿井各项指标与整体情况非常好,无任何异常,常规作业即可,但为了保护矿工人身安全与企业经济利益,对可靠性为Ⅱ级的指标进行了逐一检测分析,结果显示,该矿井的隔断风流构筑物密闭性以及防灾救灾系统存在些许不足,虽处于系统安全可靠范围内,但煤矿安全无小事,立即进行了检修,使其恢复可靠状态。经过与模型计算结果对比得出,利用本文提出的通风系统可靠性评价模型计算结果与王家岭煤矿的实际情况相符。

表3 王家岭煤矿通风系统等级的关联度
4 结论
1)通过对近年文献的分析与实地调研,运用德尔菲法建立以通风动力、通风网络、通风基础设施设备、防灾救灾系统、作业环境和人员管理因素6项2级指标以及主通风机运行稳定性、主通风机综合效率和局部风机运行合理性等29项3级指标的矿井通风系统可靠性评价指标体系。
2)综合三角模糊数确定的主观权重与熵权法确定的客观权重,解决自然语言评价的主观性问题,并通过线性加权平均计算出每个评价指标的综合权重。
3)提出基于三角模糊数-熵权法的物元可拓矿井通风系统可靠性评价模型,进一步解决评定等级不客观、不准确的问题,使评价结果更加精准。建立矿井通风系统评价指标的经典域与节域,利用王家岭煤矿的通风系统进行等级关联度计算并进行结果验证,最终求得王家岭煤矿的通风系统的可靠性等级为可靠,与该矿的实际调研结果相符,验证该方法的合理性与实用性。
