基于季节性SARIMA模型的武汉市长序列降雨量趋势分析与预测

咬登魁，段功豪

(1. 安徽省地质环境监测总站，安徽 合肥 230001；2.武汉工程大学计算机科学与工程学院，湖北 武汉 430205)

0 引言

近年来，武汉市多次受到强降雨的影响，给市民的生活与城市的发展都造成了重大的损失[1-2]。一方面，中长期高强度降雨可能会引发山体滑坡、泥石流和洪涝等自然灾害，威胁着人民的生命和财产安全；而另一方面，降雨量的减少会引发农田、河流和湖泊的干旱问题，破坏土壤原有的生态结构。如果能根据现有的降雨量的数据对未来的降雨趋势做出科学且准确可信的预测，不仅能够有效的减少暴雨洪涝和少雨干旱等自然灾害带来的巨大经济损失，而且对于工农业的发展建设、市民的出行等也具有十分重大的实际意义。然而，受下垫面性质与气候环境多样及变异的影响，降雨量的累积过程存在着大量的随机性与不确定性，目前还难以通过准确成因去预测未来某一时段的降雨，传统的趋势外预测模型也不适合该类时间序列数据的特征[3-5]。根据相关文献资料记载以及前人的经验，ARIMA模型(Autoregressive Integrated Moving Average Model，差分自回归移动平均模型)可用于非平稳数据序列的分析与预测[6]。因此，本文以武汉市2009-2019年间历年各月的降雨量为基础在对各月降雨量数据序列进行平稳性和正态分布检验的基础上进行模式识别、参数估计和模型检验等步骤，采用SPSS软件经过多次拟合选优，分别建立了多类参数支持下的季节性ARIMA模型，为武汉市的降雨气象准确预报工作提供了方法论上的一定更新。

1 SARIMA模型简介

ARIMA模型作为一类常用的随机时间序列模型，是一种精度较高的时间序列短期预测方法[7]。模型的基本思想是将预测对象随时间推移而形成的数据序列视为一个非平稳的随机序列，对该非平稳的时间序列数据进行若干次差分处理，使其变成平稳的时间序列，然后用时间序列的观测值去建立该随机过程的自回归滑动平均模型，用所建立的最优模型进行预测和分析[8-10]。而SARIMA模型，即季节性ARIMA模型，使用等于季节数的滞后差异来消除加性季节效应。该模型共有7个参数，分别是自回归阶数(p)、差分次数(d)、移动平均阶数(q)、季节性自回归阶数(P)、季节性差分次数(D)、季节性移动平均阶数(Q)和单个季节期间的移动步数(m)，记作ARIMA。其通用表达式为：

φp(B)φp(Bm)(1-B)d(1-Bm)Dyt=θq(B)ΘQ(Bm)εt

(1)

其中：

φp(B)=1-φ1(B)-φ2(B2)-…-φp(Bp)

(2)

Φp(Bm)=1-Φ1(Bm)-Φ2(B2m)-…-Φp(Bpm)

(3)

θq(B)=1-θ1(B)-θ2(B2)-…-θq(Bq)

(4)

ΘQ(Bm)=1-Θ1(Bm)-Θ2(B2)-…-ΘQ(BQm)

(5)

式(1)中：yt为所研究的时间序列数据；B表示延迟算子；)φ1，)φ2，…，)φp为自回归系数；Φ1，Φ2，…，Φp为季节性自回归系数；θ1，θ2，…，θq为移动平均系数；Θ1，Θ2，…，ΘQ为季节性移动平均系数；为白噪声序列。

SRAIMA模型较为复杂，本文采用SPSS软件里的专家建模方式和自行定阶的方式，通过比较平稳化的R方、显著性、以及正态化的BIC等参数来择优确定模型最终的参数值[11]。若显著性满足要求且BIC值较小以及R2值较大，则说明模型的拟合效果越好。BIC准则可定义为：

BIC=-2lnL+ln(n)k

(6)

式(6)中：L为模型的极大似然函数；n为样本大小；k为模型的独立参数个数。

2 研究过程

2.1 数据预处理

首先利用SPSS软件对武汉市2009-2016年各月降雨量数据序列进行绘图，如图1所示。从图上可看出，2009-2016年武汉市降雨量呈波浪式变化，整体上在每年的夏季降雨量明显增加。初步判断所研究的降雨量序列为非平稳序列，需要进行平稳化处理。

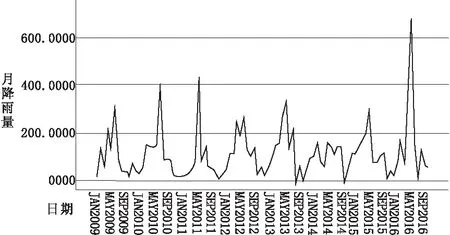
图1 武汉市2009-2016年各月降雨量时序图

图1中的时序图观察到时序数据有明显的季节性，因此数据预处理中使用季节性差分。结果如图2所示，在使用了一阶差分和一阶季节性差分后的时序图相较于图2中的序列图，序列波动更加平稳，此时认为降雨量的时间序列已经平稳，符合ARIMA模型的建模要求。

2.2 SARIMA算法参数估计与定阶

在数据预处理的过程可以得到基础模型ARIMA，模型中前后的参数“1”分别表示进行一阶差分处理和一阶季节性差分处理。根据差分后的平稳序列，绘制降雨量的自相关(ACF)图与偏相关(PACF)图，如图3和图4所示。

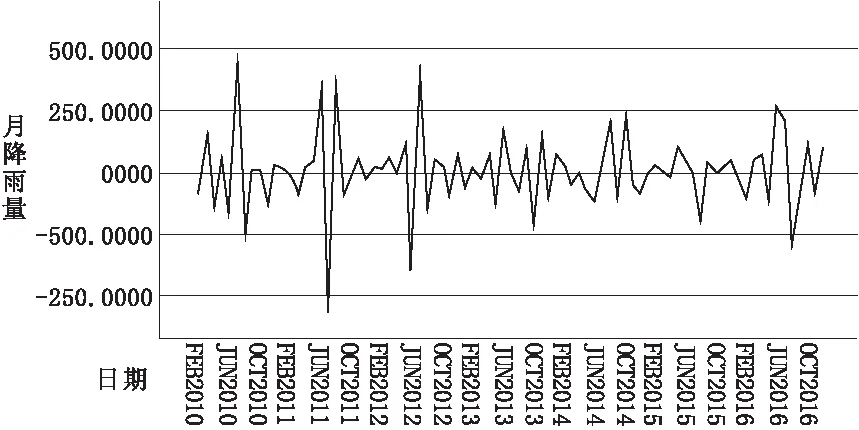
图2 武汉市2009-2016年各月降雨量一阶差分和一阶季节性差分平稳化时序图

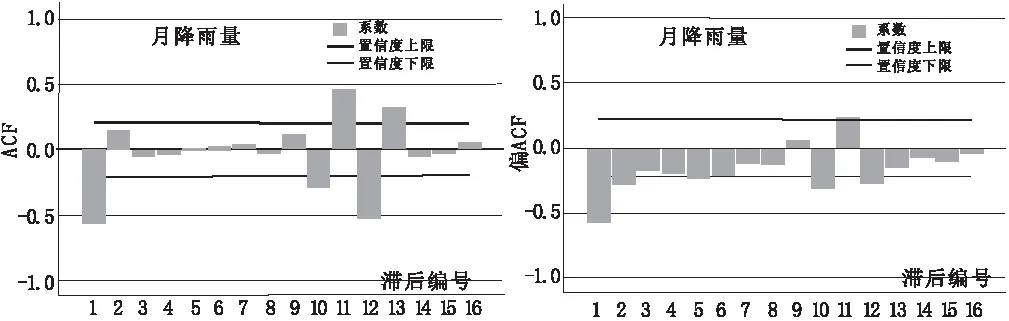
图3 平稳化序列的ACF图 图4 平稳化序列的PACF图

PACF图中延迟为1的地方有明显的突起，并且1阶延迟后基本都处于置信区间内，因此具有非季节性1阶截尾的性质，可在初步建立的模型的基础上建立ARIMA(1,1,0)(0,1,0)。反观ACF图，在滞后编号为12处有明显的突起，表明模型具有季节性MA(1)的性质，考虑进一步建立ARIMA(1,1,0)(0,1,1)。

在非季节性延迟上，分别根据图像建立ARIMA(1,1,1)(0,1,1)、ARIMA(1,1,2)(0,1,1)、ARIMA(1,1,3)(0,1,1)等不同参数下的模型以及一些衍生出来的其他模型。此处衍生出的其他模型主要是根据模型中不确定的阶数，对其进行穷举的方式进行模拟，穷举的结果并非全部都会接受，而是根据部分指标来进行筛选。此处的穷举参考了ARIMA建模中的Hyndman-Khandakar算法的思想，即使用逐步搜索来遍历模型空间，通常是对当前模型的p或者q在就近范围内进行增与减，对比模型对应的指标进行判断。根据初步拟合出的四种模型及衍生出的其他模型进行如下表1所示的各项指标的记录，为上述各种模型的指标对比。

表1 不同季节性参数下Arima模型拟合对比

以上结果中的显著性指标均大于0.05，表明结果均可以接受。其中，BIC指标最小的为模型ARIMA(1,1,1)(0,1,1)，这与使用专家建模方法拟合出的模型ARIMA(0,0,0)(0,1,1)相比略大了些，但从另一方面来看，平稳的R2指标比专家建模法要多，即拟合优度要好很多。选择R2最大的模型为ARIMA(1,1,2)(0,1,2)，因此选择该模型作为最终的降雨量预测模型。

将模型ARIMA在SPSS软件中进行具体数值的拟合，结果如下图5(a)中所示。从图中不难发现，模型对于历史降雨量的情况拟合较好。利用该模型对2017-2019年各月的降雨量进行模拟预测，图5(b)显示了武汉市2017-2019年各月的降雨量预测效果。在预测图中，红色的预测曲线与蓝色的实际值曲线的走势比较吻合。

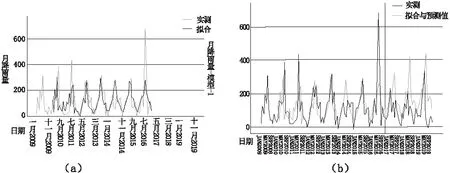
图5 ARIMA(1,1,2)(0,1,2)模型拟合和预测效果

从图5中发现，横轴上分隔线的右侧可以看出实际值与预测值的差异，虽然通过直观的观察发现结果的精准度不高，但是ARIMA模型对降雨量走势的预测比较准确，尤其是在2017年9月-2018年5月和2019年1月-2019年5月这些月份降雨量的预测走势关键点的预测精度很高。

经过上述建模及预测过程的经验总结，下一步对2020年的降雨量进行预测。首先将2009-2019年的数据作为原始数据，通过数据预处理、确定模型、模型定参和结果预测步骤，建立2020年的降雨最优季节性模型ARIMA(1,2,3)(0,1,2)如下所示。

从图5中发现，横轴上分隔线的右侧可以看出实际值与预测值的差异，虽然通过直观的观察发现结果的精准度不高，但是ARIMA模型对降雨量走势的预测比较准确，尤其是在2017年9月-2018年5月和2019年1月-2019年5月这些月份降雨量的预测走势关键点的预测精度很高。

经过上述建模及预测过程的经验总结，下一步对2020年的降雨量进行预测。首先将2009-2019年的数据作为原始数据，通过数据预处理、确定模型、模型定参和结果预测步骤，建立2020年的降雨最优季节性模型ARIMA(1,2,3)(0,1,2)如下所示。

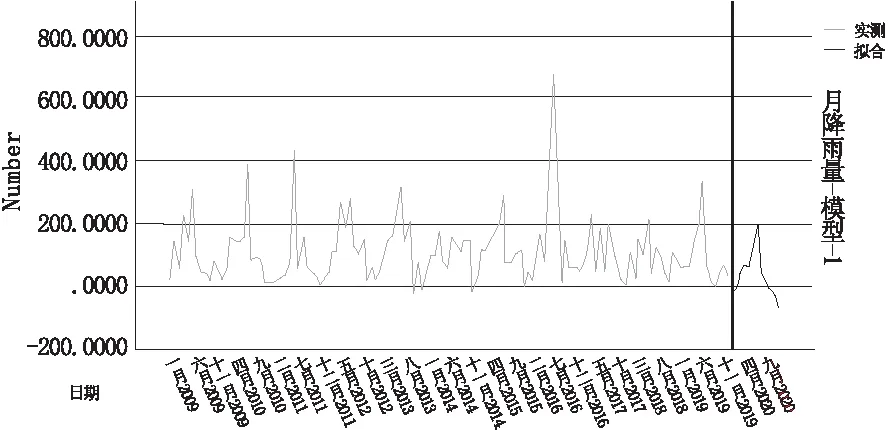
图6 武汉市2020年降雨量短期预测图

上图分隔线左侧为武汉市2009-2019年各月降雨量的数据，分隔线右侧为所预测的降雨量。从图6中不难发现，2020年降雨量的总体趋势还是同每年的一样：降雨量先增加到峰值，再逐渐减少。同时还可以发现蓝色线条在2020年初的降雨量与2020年末的降雨量均有负值，这是由于在ARIMA模型的趋势预测中，上一年的年末降雨量较少，同时降雨量的走势同样骤减，在模型确定的参数下这种减少的趋势直接持续影响到了2020年部分月份降雨量，导致数值上呈现出负值。所采用的ARIMA(1,2,3)(0,1,2)模型综合了所有衍生模型的优点，各项模型参数指标也达到了最优，对武汉市2020年月降雨量的预测是准确、有效的，本文所提供的基于降雨长序列季节性SARIMA模型的动态建立流程是一种行之有效的方法。

3 结语

通过对武汉市2009-2016年各月降雨量进行时间序列分析，在对数据进行预处理、模式识别和模型检验的基础上，选择ARIMA(1,1,1) (0,1,2)与ARIMA(1,2,3)(0,1,2)模型对武汉市降雨量进行模拟与预测。

(1)除个别年份拟合值与实际值差异较大外(如：2010、2011和2016年，出现了极端的降雨情况)，其他年份的误差都较小，说明该模型的拟合效果较好，结果比较可靠。

(2)利用ARIMA(1,1,1) (0,1,2)模型对2017-2019年武汉市各月降雨量进行预测，预测曲线与实际曲线的走势比较吻合，预测值与实际值差异较小，说明该模型具有较高的预测精度，可用于武汉市各月降雨量的预测。

(3)利用ARIMA(1,2,3)(0,1,2)模型建立2020年的降雨量预测曲线，由于前后两组实验在数据源的存在较大的差异，后者的实验数据比前者多出3年的数据，即36个实验数据，因此2020年拟合的结果也更优一些。这说明用于预测的数据数量越多，预测过程中的拟合优度越高，最终的预测精度也会相应提高。

在地理位置上与武汉临近且气候与武汉一致的其他城市也可以考虑该模型，或者得出该模型的方法进而得出具体模型来进行降雨量的预测。对于其他气候与武汉有着很大差异的城市或地区，该模型的适用性还有待进一步的验证和优化。