指数评价法和模糊数学评价法在地下水水质评价中的应用比较

孙秀国

(华北地质勘查局五一四地质大队，河北 承德 067000)

0 引言

目前，国内地下水水质评价方法主要有指数评价法、模糊数学评价法、灰色系统评价法以及模型法等[1]，其中，以指数评价法应用最广，可操作性最强，而模糊数学评价法等方法近些年来也逐渐应用于水环境质量评价领域。

1 评价方法概述

地下水水质指数评价法主要包括单因子指数评价法和综合指数评价法[1]。其中，综合指数评价法是在单因子指数评价法基础上发展而来，评价模型主要包括代数叠加型、加权均值型以及极值型[2]等，典型代表方法为极值型综合指数法中的内梅罗综合指数法；模糊数学评价法包括模糊综合评价法[3]、模糊综合概率法等，其中以模糊综合评价法为典型代表。本文以某生活垃圾填埋场周边敏感目标所在区域地下水环境质量评价为例，重点选取单因子指数评价法、内梅罗综合指数法以及模糊综合评价法三种不同方法来对填埋场周边敏感区域地下水环境质量进行评价。

1.1 单因子指数评价法

该方法数学模型简单，最能直观反映出污染物浓度值与环境质量标准之间的比值关系，但不能进行环境质量的综合评价。其计算公式如下：

(1)

式中：Ii为单因子指数；Ci为参评指标实测浓度值；Cs为参评指标所对应规范中的标准限值。

1.2 内梅罗综合指数评价法

(1)传统内梅罗指数法：该方法是环境领域常用的一种综合评价方法，由于其数学模型相对简单，计算过程易于实现，实操性较强。该模型既考虑了各指标的平均水平，也兼顾了个别指标的最大水平。

(2)

式中：N为改进后的内梅罗综合指数；Nmax为所有参评指标中单因子指数的最大值；Nave为所有参评指标中单因子指数的平均值。

(2)改进内梅罗指数法：传统内梅罗指数法未考虑权重因素，过于突出最大污染因子，而削弱其他因子的影响作用[4]，导致评价结果缺乏客观性和准确性。近年来业内人士经过不断研究探索，对该方法进行了改进和完善，改进后的内梅罗指数法计算公式如下：

(3)

(4)

(5)

式中：N改为改进后的内梅罗综合指数；Nmax为全部参评指标中单因子指数的最大值；N′ave为引入参评指标权重值后的全部参评指标中单因子指数的平均值；Li为参评指标的权重值；(SCi)max为所有参评指标相对应规范中标准限值的最大值；SCi为参评指标对应的标准限值。

1.3 模糊综合评价法

模糊综合评判法利用模糊数学理论，将定性评价转为定量评价[5]，通过隶属度的计算来确定水质类型。该方法主要评价过程：构建评价指标因子权重数据集；根据不用隶属度函数来构建模糊关系矩阵；选择合理的模糊算法构建综合评价矩阵，按照最大隶属度原则，判定最终的水质等级。

1.3.1 构建评价指标因子权重数据集

参评指标权重是指对各地下水样品进行评价分级的度量量化，计算公式如下：

(6)

式中：ui为参评指标归一化权重值；ci为参评的实测浓度值；si为参评指标所对应的各级地下水水质标准限值的算术平均值。将参评指标因子的权重值组合在一个权重集中，便构成了评价因子的权重集。

1.3.2 计算隶属度并构建模糊关系矩阵

地下水水质分级共有Ⅰ～Ⅴ级，按照不同的隶属度函数(见公式7～9)分别计算各项评价因子的隶属度，根据计算结果构建评价指标的模糊关系矩阵R。

当评价第i项因子时，其结果对标Ⅰ类水标准等级(j=1)的隶属度函数模型公式如下：

(7)

当评价第i项因子时，其结果对标Ⅱ～Ⅳ类水标准等级(j=2，3，4)的隶属度函数模型公式如下：

(8)

当评价第i项因子时，其结果对标Ⅴ类水标准等级(j=5)的隶属度函数模型公式如下：

(9)

在选择隶属函数时，因地下水质量标准中对Ⅴ类水标准限值未明确给出，使得Ⅳ类和Ⅴ类水评价隶属度函数不连续，此时需要根据函数对称性原理对Ⅴ类水质标准限值进行推定，定义Si5=2Si4-Si3[6]，进而使得Ⅳ类和Ⅴ类隶属关系连续过渡。

1.3.3 选择合理的模糊算子构建综合评级模型进行评价

本文将采用“相乘相加”算法对研究对象进行综合判定。将评价指标因子权重集U与模糊关系矩阵R相乘，然后将相乘结果进行相加并构建模糊综合模型O：

O=U⊗R={o1，o2，…，on}

(10)

选择各参评指标结果矩阵中最大值所对应的水质等级作为模糊综合评价最终结果。

2 案例应用与结果分析

2.1 研究区概况

研究区内有一处生活垃圾填埋场，周边主要敏感目标为村庄，该垃圾填埋场建设及管理方面均较为规范，目前已停止填埋。该填埋场所处位置地层岩性主要为第四系全新统粉质黏土。垃圾填埋场所在区域地下水类型为第四系孔隙水，径流方向为由北流向南，主要补给方式为大气降水。

2.2 数据来源

地下水取自填埋场所在水文地质单元内地下水流向的上、下游及两侧范围村庄饮用水井，共采集丰水期地下水样品12组。评价指标选取了生活垃圾填埋场渗滤液特征因子耗氧量(CODMn))、氨氮、硝酸盐氮、氟化物、氯化物、硫酸盐、铁、锰、总硬度及溶解性总固体共10项指标。

2.3 评价结果

2.3.1 单因子指数评价法结果

将GW1-GW12各项指标实测浓度值分别与规范中相应标准限值进行比较，得出单因子指数法评价结果(见表1)。

表1 单因子评价结果表

从评价结果来看，12组样品中大部分参评指标对应地下水水质等级在Ⅰ～Ⅲ类之间，仅GW5、GW7、GW9及GW10点位中个别指标如COD、硝酸盐氮、Fe及Mn达到Ⅳ类水，占比仅为4.16%。

2.3.2 内梅罗综合指数评价法结果

按照公式(2)～公式(5)分别对传统和改进后的内梅罗综合指数进行计算，并根据等级划分标准进行综合评价。评价结果见表2。

表2 内梅罗综合指数法评价结果表

从评价结果来看，两种方法评价结果整体较为吻合，仅GW1和GW8评价结果有所不同，改进后的内梅罗综合指数法评价结果为Ⅲ类水而传统内梅罗综合指数法评价结果为Ⅱ类，出现不同的原因是由于两种方法相对应的等级划分标准不同，传统内梅罗指数法在Ⅱ类与Ⅲ类划分标准对应的区间分别为[0.59，0.74)、[0.74，1)[7]；改进后的内梅罗指数法Ⅱ类与Ⅲ类标准对应的区间分别为[0.55，0.69)、[0.69，1)。仅GW7、GW9两件样品分别达到Ⅴ、Ⅳ类水质标准限值。

2.3.3 模糊综合评价法结果

按照前述章节相关公式(6)～公式(10)，选择合理的权重集计算模型、隶属度函数模型以及模糊算法等数学模型，对计结果按照最大隶属原则对GW1～GW12水样水质等级进行判定，其评价结果见表3。

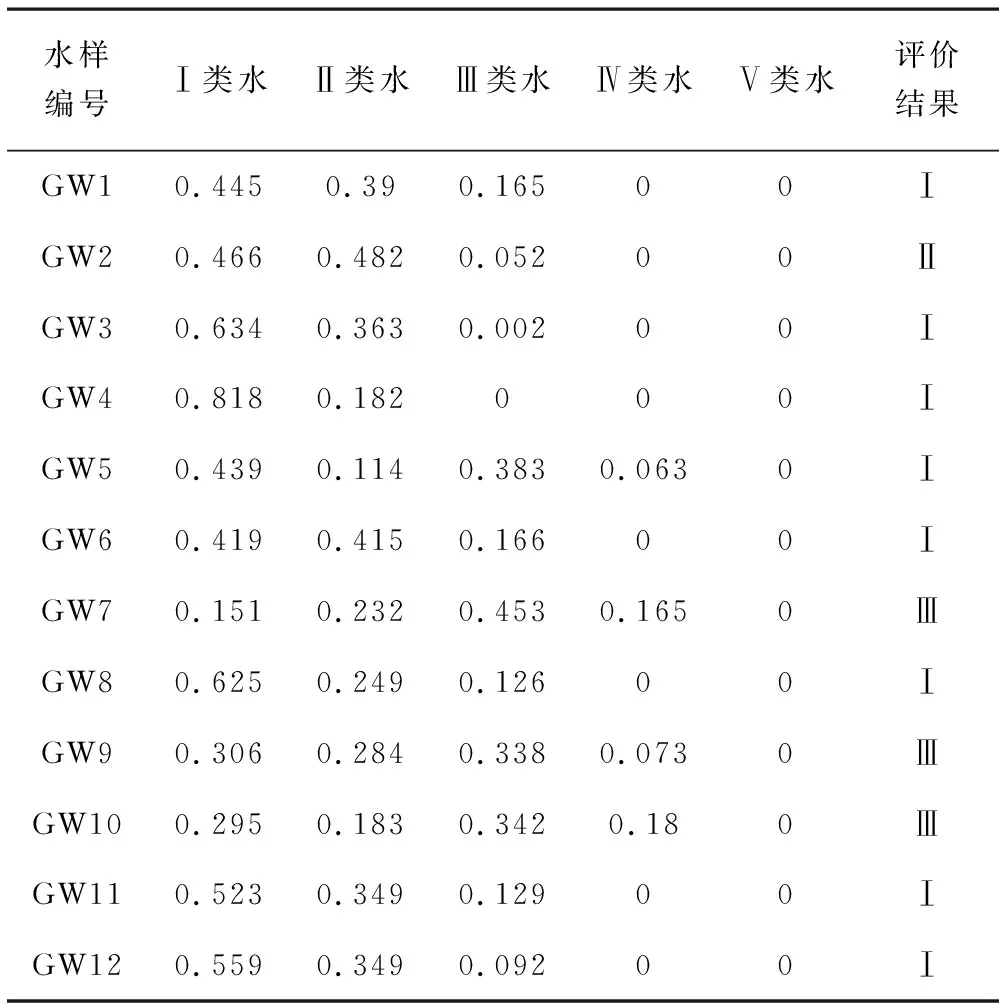
表3 模糊综合评价法评价结果表

从评价结果来看，12组样品综合评价结果均位于Ⅰ～Ⅲ类之间，其中符合Ⅰ类水等级的有8组样品，占比66.7%；符合Ⅱ类水等级的样品仅1组，占比8.3%；符合Ⅲ类水等级的样品有3组，占比25%，样品编号分别为GW7、GW9及GW10。

2.4 对比分析

通过对以上各种评价方法评价结果对比来看，单因子指数法为单项指标评价其结果与其他方法不具可比性，内梅罗综合指数法与模糊数学评价法均为水质综合评价，相比之下，两种方法评价时部分样品其综合评价结果一致，如GW3、GW4、GW6、GW11以及GW12样品其评价结果均为Ⅰ类标准；GW10样品均为Ⅲ类标准。而其他样品如GW1、GW2、GW5、GW7及GW9评价结果有所差异，但评价结果在Ⅲ类以上(含Ⅲ类)的样品中均出现在GW7、GW9及GW10。说明这三组水样水质质量相对其他样品来说要差。总体来看，模糊综合评价法评价结果水质质量状况要优于其他两种内梅罗综合指数法评价结果。

3 结语

本文通过指数法和模糊数学的方法对某生活垃圾填埋场周边村庄地下水环境质量状况进行评价并得出以下结论：

(1)单因子指数法可直观体现地下中超标因子项目和超标污染物分布范围，在评价某项污染物污染程度时可结合超标倍数进行评价，但该方法对于同一等级水样的水质状况无法进行评价，也无法对某一水样的综合水质状况进行评价。

(2)传统和改进后的内梅罗综合指数法因其评价模型相对模糊综合评价法计算过程简单，应用性较广。改进后的内梅罗综合指数法还引入了各项指标的权重值，相对传统内梅罗评价模型来说更具说服力，但从根本上来说，内梅罗评价模型是一种极值型的评价方法，评价过程中可能会由于参评指标浓度值过高，而导致整体水质状况评价等级较差。此外，传统和改进后的内梅罗综合指数对应水质等级划分标准并不统一，可能导致污染指数相差不大的水质分属不同的两个等级。

(3)模糊综合评价法利用模糊数学的方法，解决了定性标准等级难以定量化的问题。相对于单因子指数法和内梅罗综合指数法来说，该方法计算过程较复杂，当评价数据样本数量较多时，需要借助计算机编程语言来完成，计算难度将会加大，但其评价结果更符合实际情况。