导数与不等式的证明及恒成立问题中的易错题剖析

■河南省许昌市建安区第一高级中学 练中彬

导数与不等式的证明及恒成立问题是高考考查的重点内容之一,也是同学们学习的难点,该类题主要涉及函数、方程、导数等知识,也涉及构造函数、数形结合、分类讨论、分离参数、放缩、转化等方法,对提升同学们的逻辑推理与数学运算有极大的帮助。下面就导数与不等式的证明及恒成立问题中的易错点归类总结。

一、构造函数证明不等式

例1证明:当x＞1时,+lnx＜。

易错剖析:当待证不等式的两边含有同一个变量时,一般地,可以直接构造“左减右”或“右减左”的函数,通过研究其单调性等相关函数性质证明不等式。

二、放缩法证明不等式

例2已知函数f(x)=lnx-ax+1。

(1)若对任意x∈(0,+∞),f(x)≤0恒成立,求a的取值范围;

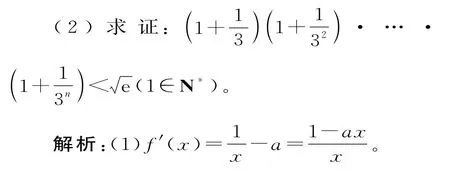
若a≤0,当x＞1时,lnx-ax+1＞0,不符合题意。

综上可得,a的取值范围为[1,+∞)。

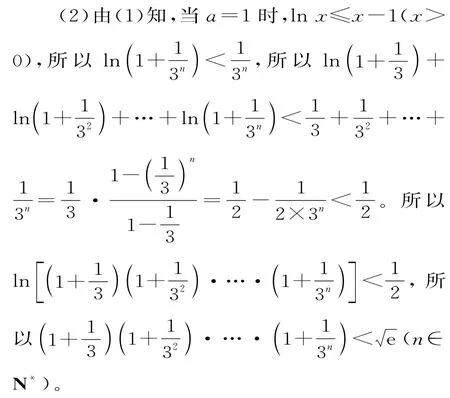
易错剖析:解答本题第(2)问的关键是利用lnx≤x-1(x＞0)进行放缩。

例3已知f(x)=aex-lnx-1。证明:当a≥时,f(x)≥0。

证明:当a≥时,f(x)≥-lnx-1(x＞0)。

设g(x)=-lnx-1(x＞0),则g＇(x)=。

当0＜x＜1时,g＇(x)＜0;当x＞1 时,g＇(x)＞0。所以x=1是g(x)的极小值点,也是最小值点。

故当x＞0时,g(x)≥g(1)=0。

因此,当a≥时,f(x)≥0。

易错剖析:若某些不等式直接构造函数不易求最值,则可利用条件与不等式的性质,适当放缩后,再构造函数进行证明。

三、分离ex 和lnx 证明不等式

例4已知函数f(x)=ex2-xlnx,证明:当x＞0时,f(x)＜xex+。

再令φ(x)=ex-ex,则φ＇(x)=e-ex,易知φ(x)在(0,1)上单调递增,在(1,+∞)上单调递减,则φ(x)max=φ(1)=0,所以exex≤0。

因为h(x)与φ(x)不同时为0,所以exex＜lnx+,故原不等式成立。

易错剖析:(1)当直接求导比较复杂或无从下手时,可将待证式进行变形,构造两个都便于求导的函数,从而找到可以传递的中间量,达到证明的目的。(2)本题中将原不等式化为lnx+＞ex-ex(x＞0)(分离lnx与ex),便于探求构造的函数h(x)=lnx+和φ(x)=ex-ex的单调性,分别求出h(x)的最小值与φ(x)的最大值,借助“中间媒介”证明不等式。

四、分拆函数法证明不等式

例5已知函数f(x)=elnx-ax(a∈R)。

(1)讨论函数f(x)的单调性;

(2)当a=e 时,证明:xf(x)-ex+2ex≤0。

解析:(1)f＇(x)=-a(x＞0)。

若a≤0,则f＇(x)＞0,所以f(x)在(0,+∞)上单调递增。

若a＞0,则当0＜x＜时,f＇(x)＞0;当x＞时,f＇(x)＜0。所以f(x)在上单调递增,在上单调递减。

(2)因为x＞0,所以只需证f(x)≤-2e。

当a=e时,由(1)知,f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,所以f(x)max=f(1)=-e。

设g(x)=-2e(x＞0),则g＇(x)=。

当0＜x＜1时,g＇(x)＜0,g(x)单调递减;当x＞1 时,g＇(x)＞0,g(x)单调递增。所以g(x)min=g(1)=-e。

综上可得,当x＞0时,f(x)≤g(x),即f(x)≤-2e,即xf(x)-ex+2ex≤0。

易错剖析:①当直接求导比较复杂或无从下手时,可将待证式进行变形,构造两个都便于求导的函数,从而找到可以传递的中间量,达到证明的目的。②在证明的过程中,等价转化是关键,在证得g(x)min≥f(x)max恒成立时,可以得到f(x)≤g(x)恒成立。

五、不等式恒成立问题

例6已知函数f(x)=x2+,若∀x1∈[1,2],∃x2∈[-1,1],使f(x1)≥g(x2),求实数m的取值范围。

解析:若∀x1∈[1,2],∃x2∈[-1,1],使f(x1)≥g(x2),则需f(x1)min≥g(x2)min。