Logistic回归联合ROC曲线模型在雷电潜势预报中的应用

吴安坤，郭军成，黄天福

(1.贵州省气象灾害防御技术中心，贵州 贵阳 550081；2.贵州省安顺市气象局，贵州 安顺 561000；3.贵州省六盘水市气象局，贵州 六盘水 553000)

0 引言

雷暴活动作为常见的强对流天气过程，造成的灾害是联合国公布的十大最严重的自然灾害之一。随着社会经济不断发展，每年因强对流天气过程造成的损失越加严重。因此，加强雷暴活动的预测预报，对防灾减灾有十分重要的指导意义。雷暴云的发生发展伴随着不稳定环境中气团的抬升，探空资料观测大气中的温湿压、水汽和抬升等物理量参数，对研究局地雷电潜势预报具有很好的指示作用[1-4]。目前采用探空对流参数开展的雷暴预报研究，大多直接采用多元统计线性回归方法，需解决雷暴发生与否的非线性与探空资料之间的线性回归问题。线性回归模型要求因变量是连续的正态分布变量，且自变量和因变量之间呈现线性关系。当因变量为分类型变量，且自变量与因变量没有线性关系时，线性回归模型的假设条件就会遭到破坏。而采用Logistic回归分析模型可以很好地解决此类问题，它对因变量的分布没有要求，巧妙地避开了分类型变量的分布问题。Logistic回归作为一种非线性概率性预测模型，可实现对研究观察结果进行分类、处理协变量之间的多变量分类分析[5]，被广泛用于流行病学的病因研究中，分析疾病与危险因素间联系，所观测的因素常以二分变量取值，如生存与死亡、是否发病等，即因变量为0或者1。如罗蒙等[6]将具有统计学意义的检查指标纳入多因素Logistic 回归分析，预测新型冠状病毒肺炎患者发生危重症的风险。而ROC曲线是目前学术界公认的诊断价值最佳的方法，其操作简便，且具有通过图形就能够判断分析的诊断性能[7-9]。宗迎迎等[10]应用Logistic 回归和ROC曲线研讨血清Dickkopf、高尔基体糖蛋白73和甲胎蛋白对原发性肝癌的诊断价值。张宇等[11]应用Logistic 模型联合ROC 曲线法对新型冠状病毒肺炎严重程度进行判别，具有较高的正确率。引入Logistic回归联合ROC曲线模型采用探空物理量资料开展雷电潜势预报研究，分析雷电活动有、无问题，目前未见相关技术研究。因此，本文选取闪电监测资料和探空观测参数，筛选数据样本纳入单因素逻辑回归模型，选取有统计学意义的参数纳入多因素逻辑回归模型，采用ROC曲线联合二分类Logistic回归模型开展雷暴活动潜势预报研究。

1 数据来源及处理

探空资料来源于Micaps系统提供的T-lnp探空数据，提取贵阳站2020年1—10月逐日08时和20时的修正总指数、K指数、沙氏指数、Faust指数、最大抬升指数、对流稳定度指数等72种物理参数。为保证数据的可靠性，采用四分位检测异常值，剔除上四分位+1.5 IQR距离、下四分位-1.5 IQR距离以外时刻的数据。闪电资料来源于贵州省闪电监测网，考虑实际业务中T-lnp探空数据每天主要包括08时和20时2个时次，以及探空站之间的距离。规定该站当日08时或20时以后12 h内、100 km范围内若发生50次以上的闪电，则将当日08时或者20时对应的物理参量作为1个雷暴天气样本，反之为非雷暴天气。本文通过筛选得到294个雷暴、238非雷暴天气样本以及对应的72个物理参数值、闪电活动次数。

2 分析方法

以筛选的样本中72个对流参数为因变量，纳入单因素逻辑回归模型，筛选变量，将有显著性统计学意义(P<0.001) 的变量纳入多因素逻辑回归模型，选取满足一定检验条件的参数代入模型计算概率预测值。以此概率预测值为检验变量，样本雷暴活动情况为状态变量，绘制ROC曲线，以敏感度与特异性之和最大所对应的概率值作为截断值，纳入气象预报质量评分检验。

2.1 Logistic 模型联合ROC曲线法

假设雷暴发生情况y，发生为1，未发生为0。影响雷暴发生情况y的m个对流参数分别为x1，x2，…,xm。雷暴活动发生的概率记为P(y=1|xi)=Pi,发生与否的2个概率分别为：

(1)

(2)

其中Pi代表在第i个观测中雷暴发生的概率，1-Pi对应雷暴未发生的概率，均为对流参数xi构成的非线性函数。雷暴发生与不发生的概率之比Pi/(1-Pi)，称为事件的发生比(Odds)，对Odds取对数变换，得到逻辑回归模型的线性模式如下：

(3)

得到雷暴活动发生概率P如下所示：

(4)

ROC 曲线(receiver operating characteristic curve)分析被认为是一种诊断试验评价中理想和经典的方法。其思路是以逻辑回归模型所得的预测概率为基础，选取不同截断值按照表2描述的雷暴预报混淆矩阵进行统计，计算不同截断值下的敏感度与特异度。

表2 探空物理量参数为因变量构建单因素、多因素逻辑回归模型Tab.2 Single factor and multi factor Logistic regression models with sounding physical parameters as dependent variables

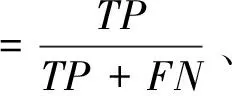
2.2 气象预报检验

对于雷电等强对流天气的小概率时间检验采用Donaldson[13]提出的方法，计算命中率(POD)、虚警率(FAR)、临界成功指数(CSI)、失误率(FOM)衡量预报方程的准确率和进行预报质量评分。在表1混淆矩阵的基础上，计算POD、FAR、CSI、FOM如下所示：

表1 混淆矩阵Tab.1 Confusion matrix

(5)

(6)

(7)

(8)

3 结果分析

3.1 Logistic回归分析模型

通过单因素分析显示瑞士第二雷暴指数(SWISS12)、瑞士第一雷暴指数(SWISS00)、抬升指数(LI)、最大抬升指数(BLI)、条件对流稳定度指数(IL)、沙氏指数(SI)、通气管指数(TQG)、修正杰弗逊指数(TMJ)、Faust指数(Faust)、修正对流指数(DCI)、修正K指数(mK)、抬升凝结处温度(TCL_T)、对流凝结高度处温度(CCL_T)、整层比湿积分(IntegralQ)14个对流参数，有统计学意义(均有P<0.001)，即以上14个参数对雷暴活动趋势有指示作用，涉及大气热力因子、动力条件及综合指数等，可综合反映中低层热动力稳定度特性。其中SWISS12、SWISS00、LI、BLI、IL、SI6个参数OR<1，表征参数越小，发生雷暴活动的可能性越大；反之其他8个参数值越大，发生雷暴活动的可能性越大。进一步对有统计学意义的14个参数采用多因素分析，结果显示SWISS00(OR=0.74，95%CI：0.58～0.94，P<0.05)、LI(OR=0.65，95%CI：0.45～0.96，P<0.05)、BLI(OR=0.81，95%CI：0.71～0.92，P<0.05)、IntegralQ(OR=1.00，95%CI：0.90～1.20，P<0.05)4个参数为雷电潜势预报多参数逻辑回归指标，即ln(p/(1-p))=0.306×SWISS00+0.424×LI+0.214×BLI-0.001×IntegralQ。

3.2 ROC曲线

在概率截断值为0.5水平下，如表3所示，单因素构建逻辑回归模型预准确度介于68.2%～75.4%，ROC曲线的曲线下面积介于0.751～0.793，以整层比湿积分相对最好、沙氏指数相对最差。若以整层比湿积分(IntegralQ)作为单因素指标开展雷电潜势预报，准确度为75.4%。

表3 单因素指标ROC曲线下的面积Tab.3 Area under ROC curve of single factor index

采用多因素逻辑回归模型，ROC曲线的曲线下面积为0.839(0.804～0.875)，P<0.001，预测能力较单因素模型有所提高，具有较好的预测价值(图1)。当Logistic回归分析模型得到的预测值为0.611时，其敏感度为0.789，特异度为0.799，二者之和最大，因此将该值作为最佳临界点将研究对象分为2组，即Logistic回归分析模型预测概率值≥0.611认为有雷电天气过程，在此条件下，准确度由单因素的75.4%提高到79.5%。

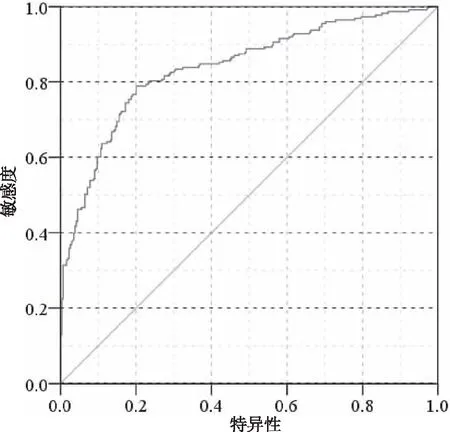
图1 多因素逻辑回归ROC曲线Fig.1 Multivariate Logistic regression ROC curve

3.3 预报质量校验

根据确定的概率截断值0.611，在混淆矩阵的基础上统计TP为247、FP为47、FN为62、TN为176，采用气象预报评分计算命中率(POD)为84.01%、虚警率(FAR)为26.05%、临界成功指数(CSI)69.38%、失误率(FOM)为20.06%。

4 结论与讨论

本文选取72个探空物理量参数作为自变量，闪电监测系统探测是否发生闪电作为因变量，将单因素指标逐一纳入逻辑回归模型，筛选具有显著性统计学意义(P<0.001)的指标进入多因素回归模型，选取满足检验条件P<0.05的参数得到雷电潜势预报模型ln(p/(1-p))=0.306×SWISS00+0.424×LI+0.214×BLI-0.001×IntegralQ。得到结论如下：

①多因素逻辑回归模型预警效果优于单因素模型，预警准确度从75.4%提高到79.5%。

②联合ROC曲线确定预报模型的概率阈值为0.611，雷电潜势预报的命中率POD为84.01%，虚假警报率FAR为26.05%，临界成功指数CSI为69.38%。准确率较高，雷电潜势预报具有较好的预报能力。

Logistic回归模型处理“二分类”问题，旨在拟合结果的“有”“无”问题，有效弥补了线性回归的缺陷；同时结合ROC曲线对模型进行检验，确定合适的预测概率值，可进一步提高预警准确率。Logistic回归模型联合ROC曲线法在气象预测预报，特别是非线性预测中有一定的应用价值。